Answers
Answer:
Step-by-step explanation:
180-110+70
Related Questions
Seema deposited $800 in a saving account earning 2.88% compounded annually. To the nearest cent, how much will she have in 16 years? Do not include the dollar sign in your answer.
Answers
Answer:
1260.04
Step-by-step explanation:
The formula for compound interest is:
A = P(1+\(\frac{r}{n}\)\()^{nt}\) where A is the final amount, P is the initial principal balance, r is the interest rate, n is the number of times interest applied per time period and t is the number of time periods elapsed. Since the deposit was compounded annually, just like the interest, we can omit the n in the equation.
Applying the formula to question:
800(1+\(\frac{2.88}{100}\)\()^{16}\) = 1260.04 (rounded off to nearest cent since it's money)
Corey is dropping off his dry cleaning. If Corey has 12 lbs of dark clothes and 4 lbs of whites, what is the ratio of pounds of dark clothes to pounds of white?
A. 3:1
B. 4:1
C. 6:2
D. 12:4
Answers
The ratio of pounds of dark clothes to pounds of white clothes is 3:1, which is option A
To find the ratio of pounds of dark clothes to pounds of white clothes, we need to divide the pounds of dark clothes by the pounds of white clothes.
Given that Corey has 12 lbs of dark clothes and 4 lbs of whites.
So, the ratio of pounds of dark clothes to pounds of white clothes = 12/4.
Simplifying this ratio, we get:
Ratio of pounds of dark clothes to pounds of white clothes = 3/1
Therefore, the ratio of pounds of dark clothes to pounds of white clothes is 3:1, which is option A.
This means that for every 3 pounds of dark clothes, Corey has 1 pound of white clothes. Ratios are a way to compare two quantities, and they can be expressed in different ways, such as in fraction or in the form of a colon. In this case, the ratio is 3:1, which means that for every 3 pounds of dark clothes, there is 1 pound of white clothes.
To learn more about ratio:
https://brainly.com/question/13419413
#SPJ9
The probability that a student has a Visa card (event V) is .76. The probability that a student has a Master card (event M) is .16. The probability that a student had both is .04.
Answers
Answer:
The Probability of both happening is 0.304.
Step-by-step explanation:
P(A) × P(B)
= 0.76 × 0.4
= 0.304
Which graph has the same end behavior as f (x) = StartFraction negative 6 x Superscript 5 Baseline minus x cubed + 7 x Over 2 x squared + 1 EndFraction


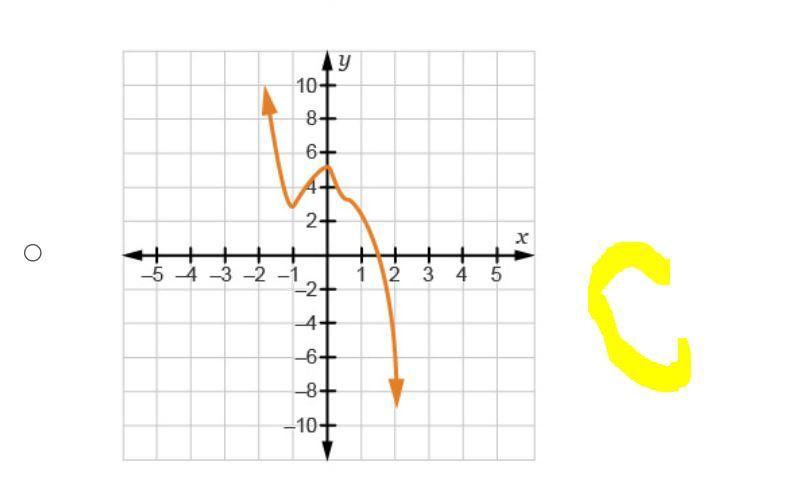

Answers
The graph with the same end behavior is the one in option C.
Which graph has the same end behavior?The given function has a numerator with a negative leading coefficient and an odd degree, while the denominator is a quadratic polynomial.
It will mean that as x tends to negative infinity, the function tends to infinity, and as x tends to positive infinity, the function tends to negative infinty, that is the end behavior of the given function.
The graph with that end behavior is the same one than in option C.
Learn more about end behavior:
https://brainly.com/question/1365136
#SPJ1
An IQ test is designed so that the mean is 100 and the standard deviation is 15 for the population of normal adults. Find the sample size necessary to estimate the mean IQ score of the residents of a state if you want to be 95% confident that the sample mean is within 4 IQ points of the true mean.
What is the required sample size?
Answers
Answer:
55
Step-by-step explanation:
\(\displaystyle MOE = z\biggr(\frac{\sigma}{\sqrt{n}}\biggr)\\\\4=1.96\biggr(\frac{15}{\sqrt{n}}\biggr)\\\\4=\frac{29.4}{\sqrt{n}}\\\\\sqrt{n}=\frac{29.4}{4}\\\\\sqrt{n}=7.35\\\\n=54.0225\\\\n\approx55\uparrow\)
Make sure to always round up the required sample size to the nearest integer!
Is the data set approximately periodic?
If so, what are its period and amplitude?
Hour
Number of cars
1 2 3
4
5
6
7 8 9 10 11 12
52 76 90 75 91 104 89 105 119 103 121 135

Answers
The data set is approximately periodic with a period of 3 and an amplitude of about 7.5.
How to explain the valueThe period is the length of time it takes for the data to repeat itself. In this case, the data repeats itself every 3 hours. The amplitude is the distance between the highest and lowest values in the data set. In this case, the amplitude is about 7.5 cars.
Hour | Number of cars
------- | --------
1 | 90
2 | 52
3 | 76
4 | 75
5 | 91
6 | 104
7 | 89
8 | 105
9 | 119
10 | 103
11 | 121
12 | 135
As you can see, the data repeats itself every 3 hours. The highest value in the data set is 135 cars, and the lowest value is 52 cars. The difference between these two values is 83 cars, which is about 7.5 times the average number of cars (90 cars). Therefore, the amplitude of the data set is about 7.5 cars.
Learn more about amplitude on
https://brainly.com/question/3613222
#SPJ1
Charlie does the following problem:
3^3 · 3^2 = 3 6 = 3 · 3 · 3 · 3 · 3 · 3 = 729.
Which of the following is a true statement?
He is incorrect because he should have 3 factors of 6.
He is correct.
He is incorrect because he should have 6 factors of 9.
He is incorrect because he should have only 5 factors of 3.
Answers
He is incorrect because he should have 6 factors of 9.
Answer:
I think he is incorrect because 3x3 x 3x2 only equals 0.16. So I think it is answer 3.
Step-by-step explanation:
WHO WANTS BRAINLIST??
Answers
Answer:
Me please
Step-by-step explanation:
I like ice cream :D
Answer:
I do!!! Please may I get it? If someone else asked and you chose them that's fine!
Step-by-step explanation:
(The upcoming and this sentence is pre-written and copy and pasted in every brainly question or comment I write or answer.) If this answer helped you please consider giving it brainliest.
- •Trix•
( Yes I know my - •Trix• thingy is not my user but its what I would change it to if I could but I can't, please address me as Trix while commenting or talking to me here.)
Find: 11/3 divided by 2/3
The quotient is 5 and ______
Answers
Answer:
1/2
Step-by-step explanation:
11/3 divided by 2/3
=5.5
11/3 divided by 2/3 , the quotient is 5 and remainder is 1.
The divisor is the integer that divides a given number. The resultant number is sometimes referred to as the quotient. The residual is the number that the divisor leaves after partially dividing the original integer.
Let, first number is x and second number is y
On dividing given two number
Division=x/y
\(x/y=\frac{11/3}{2/3}\)
\(x/y=11/2\)
It is given that the quotient for dividing two numbers is 5.
Using,
Dividend = Divisor x Quotient + Remainder
Here,
Dividend =11
Divisor =2
Quotient =5
On, substituting these values to get Remainder
11=2 x 5+ Remainder
Remainder=1
Thus, remainder is 1.
Learn more about mathematical operation, here:
https://brainly.com/question/29635854
#SPJ6
What is the midpoint of the line segment with the given endpoints (4,6) (3,-3)
Help it’s urgent
Answers
The coordinates of the midpoints of the given line segment is:
(3.5, 1.5)
How to find the midpoints of a line segment?The midpoint of a line segment is simply referred to as the center of that specific line segment.
Thus, the coordinates at that point will be referred to as the coordinates of the midpoint.
The coordinates of the endpoints of the line are:
(4,6) and (3,-3)
The formula to find the coordinates of the midpoint of the line is:
(x, y) = (x₁ + x₂)/2, (y₁ + y₂)/2
Thus, we have:
(x, y) = (4 + 3)/2, (6 - 3)/2
= (3.5, 1.5)
Read more about Midpoint of Line segment at: https://brainly.com/question/896396
#SPJ1
Katie just opened a checking account at the bank. Within the first month, she deposited three checks for $21.68, $42.09, and $65.44. She withdrew $4.64 for new pencils, $23.11 for earbuds, and $9.78 for movies from her account in the same month.
Answers
Complete question is;
Katie just opened a checking account at the bank. Within the first month, she deposited three checks for $21.68, $42.09, and $65.44. She withdrew $4.64 for new pencils, $23.11 for earbuds, and $9.78 for movies from her account in the same month.
Write Katie’s withdrawals as negative rational numbers and her deposits as positive rational numbers.
Answer:
Deposits are; +21.68, +42.09, and +65.44.
Withdrawals are; -4.64, -23.11, and -9.78
Step-by-step explanation:
We are told that the deposits are;
$21.68, $42.09, and $65.44.
Now, she withdrew $4.64 for new pencils, $23.11 for earbuds, and $9.78 for movies from her account in the same month.
We are told to write Katie’s withdrawals as negative rational numbers and her deposits as positive rational numbers.
A rational number is a number that can be expressed as the ratio of two integers. In this question, by inspection, all the given values for deposits and withdrawals can be expressed as the ratio of 2 integers.
Thus;
Deposits are; +21.68, +42.09, and +65.44.
Withdrawals are; -4.64, -23.11, and -9.78
A school board member surveys parents to learn how they feel about the new school boundaries. What are a random sample and a non-random sample for this situation?
Answers
A random sample and a non-random sample for this situation are given below:
Mrs.Donovan could have taken opinions from the first 50 parents to answer.Mr.Giles could have taken 10 Parents from each grade in the school and used that as his example.What is a Random Sample?This refers to the statistical population where there is an equal chance of being selected by members of a population.
Hence, we can see that a random sample and a non-random sample for this situation are given above and this shows that each of them have equal chances of being selected (random sampling)
Read more about random samples here:
https://brainly.com/question/17831271
#SPJ1
Write an equation of the line with a slope -1/2 and a y-intercept of 1
Answers
Answer: y = -0.5x +1
Step-by-step explanation:
Rectangles abcd and klmn are similar. If their permitted are 20 and 16, and the area of the larger rectangle is 25, what is the area of the smaller rectangle?
Answers
The area of the smaller rectangle (KLMN) is 16.
Since rectangles ABCD and KLMN are similar, their corresponding sides are proportional.
Let's assume the length of side AB in rectangle ABCD is x, and the length of side KL in rectangle KLMN is y.
We can set up the proportion:
(x/y) = (20/16)
To find the area of the smaller rectangle, we need to determine the ratio of their areas.
Since the area of a rectangle is given by the product of its length and width, the ratio of the areas will be equal to the square of the ratio of their sides:
(Area of ABCD)/(Area of KLMN) = (x²)/(y²)
We are given that the area of ABCD is 25, so we have:
25/(Area of KLMN) = (x²)/(y²)
To find the area of KLMN, we need to substitute the values of x and y from the proportion:
25/(Area of KLMN) = (20/16)²
Simplifying the right side:
25/(Area of KLMN) = (5/4)²
25/(Area of KLMN) = 25/16
Cross-multiplying:
25 × 16 = 25 × (Area of KLMN)
400 = 25 × (Area of KLMN)
Dividing both sides by 25:
16 = Area of KLMN
Therefore, the area of the smaller rectangle (KLMN) is 16.
Learn more about similarity click;
https://brainly.com/question/26451866
#SPJ1
Let L be the line with parametric equations x=5+t,y=6,z=−2−3t. Find the vector equation for a line that passes through the point P=(−5,7,−8) and intersects L at a point that is distance 3 from the point Q=(5,6,−2). Note that there are two possible correct answers. Use the square root symbol √ where needed to give an exact value for your answer.
Answers
Answer:
The required equations are
\((-5 \hat i + 7 \hat j + 8 \hat k )+\lambda \left((10+\frac {3}{\sqrt {10}})\hat i -\hat j +(6- \frac {9}{\sqrt {10}})\hat k\right)=0\) and
\((-5 \hat i + 7 \hat j + 8 \hat k )+\lambda \left((10-\frac {3}{\sqrt {10}})\hat i -\hat j +(6+ \frac {9}{\sqrt {10}})\hat k\right)=0\).
Step-by-step explanation:
The given parametric equation of the line, \(L\), is \(x=5+t, y=6, z=-2-3t,\) so, an arbitrary point on the line is \(R(x,y,z)=R(5+t, 6, -2-3t)\)
The vector equation of the line passing through the points \(P(-5,7,-8)\) and \(R(5+t, 6, -2-3t)\) is
\(\vec P + \lambda \vec{(PR)}=0\)
\(\Rightarrow (-5 \hat i + 7 \hat j - 8 \hat k )+\lambda \left((5+t-(-5))\hat i + (6-7)\hat j +(-2-3t-8)\hat k\right)=0\)
\(\Rightarrow (-5 \hat i + 7 \hat j - 8 \hat k )+\lambda \left((10+t)\hat i -\hat j +(6-3t)\hat k\right)=0\;\cdots (i)\)
The given equation can also be written as
\(\frac {x-5}{1}=\frac {v-6}{0}=\frac{z+2}{-3}=t \; \cdots (ii)\)
The standard equation of the line passes through the point \(P_0(x_0,y_0,z_0)\) and having direction\(\vec v= a_1 \hat i +a_2 \hat j +a_3 \hat k\) is
\(\frac {x-x_0}{a_1}=\frac {y-y_0}{a_2}=\frac{z-z_0}{a_3}=t \;\cdots (iii)\)
Here, The value of the parameter,\(t\), of any point \(R\) at a distance \(d\) from the point, \(P_0\), can be determined by
\(|t \vec v|=d\;\cdots (iv)\)
Comparing equations \((ii)\) and \((iii)\)
The line is passing through the point \(P_0 (5,6,-2)\) having direction \(\vec v=\hat i -3 \hat k\).
Note that the point \(Q(5,6,-2)\) is the same as \(P_0\) obtained above.
Now, the value of the parameter, \(t\), for point \(R\) at distance \(d=3\) from the point \(Q(5,6,-2)\) can be determined by equation \((iv)\), we have
\(|t(\hat i -3 \hat k)|=3\)
\(\Rightarrow t^2|(\hat i -3 \hat k)|^2=9\)
\(\Rightarrow 10t^2=9\)
\(\Rightarrow t^2=\frac {9}{10}\)
\(\Rightarrow t=\pm \frac {3}{\sqrt {10}}\)
Put the value of \(t\) in equation \((i)\), the required equations are as follows:
For \(t= \frac {3}{\sqrt {10}}\)
\((-5 \hat i + 7 \hat j - 8 \hat k )+\lambda \left((10+\frac {3}{\sqrt {10}})\hat i -\hat j +\left(6-3\times \frac {3}{\sqrt {10}})\hat k\right)=0\)
\(\Rightarrow (-5 \hat i + 7 \hat j - 8 \hat k )+\lambda \left((10+\frac {3}{\sqrt {10}})\hat i -\hat j +(6- \frac {9}{\sqrt {10}})\hat k\right)=0\)
and for \(t= -\frac {3}{\sqrt {10}}\),
\((-5 \hat i + 7 \hat j - 8 \hat k )+\lambda \left((10+\left (-\frac {3}{\sqrt {10}}\right))\hat i -\hat j +(6-3\times \left(-\frac {3}{\sqrt {10}}\right)\hat k\right)=0\)
\(\Rightarrow (-5 \hat i + 7 \hat j - 8 \hat k )+\lambda \left((10-\frac {3}{\sqrt {10}})\hat i -\hat j +(6+ \frac {9}{\sqrt {10}})\hat k\right)=0\)
Would love for an expert to verify my solutions:High school trig.

Answers
The entered responses are correct
Explanation:Write out the points from the given information to see the nature of the ellipse as follows:
\(\begin{gathered} x=4\cos\frac{\pi}{2}=0 \\ \\ y=3\sin\frac{\pi}{2}=3 \\ \\ (x,y)=(0,3) \end{gathered}\)\(\begin{gathered} x=4\cos\pi=-4 \\ \\ y=3\sin\pi=0 \\ \\ (x,y)=(-4,0) \end{gathered}\)\(\begin{gathered} x=4\cos\frac{3\pi}{2}=0 \\ \\ y=3\sin\frac{3\pi}{2}=-1 \\ \\ (x,y)=(0,-1) \end{gathered}\)Compute the following sum of a geometric sequence: S = 0.936 + 0.935 + ... + 0.92 + 0.9 + 1 (Round your answer to two decimal places.)
Answers
The sum of the given geometric sequence to 2 dp is 936.00
To get the sum of a geometric sequence, we will use the formula for calculating the sum to infinity of the sequence as shown:
\(S_\infty=\frac{1}{1-r}\)
a is the first term
r is the common ratio
Given the sequence S = 0.936 + 0.935 + ... + 0.92 + 0.9 + 1
a = 0.936
r = 0.935/0.936 = 0.998
Substitute into the formula
\(S_\infty=\frac{0.936}{1-0.999}\\S_\infty=\frac{0.936}{0.001}\\S_\infty=936\)
Hence the sum of the given geometric sequence to 2 dp is 936.00
Learn more here: https://brainly.com/question/24643676
Please, help me find the answer

Answers
The probability values for the questions posed are :
11/20probability of Public speaking given that student is majoring in Business Administration1/3A.)
Number of students Taking a public speaking class majoring in business administration.
10 + 45 = 55P(PS or BA) = 55/100 = 11/20
Therefore, the probability of PS or BA is 11/20
B.)
For the survey described, P(taken a public speaking class | majoring in Business Administration) represents the probability that a selected student has taken a public speaking class given that the student is majoring in business administration.
Hence, as inferred from P(A|B) ; probability of A given B.
C.)
P(PS|BA) = n(PSnBA) / n(BA)
n(PS) = 10+20 = 30
n(PSnBA) = 10
P(PS|BA) = 10/30 = 1/3
Therefore , the probability of PS|BA is 1/3.
Learn more on probability:https://brainly.com/question/24756209
#SPJ1
Let be independent random variables with the common distribution function F and suppose they are independent of a geometric random variable with parameter p. Let M = max(x1,....,xN) (a) Find P{M<} by conditioning on N (b) Find P(M1} (d) Use (b) and (c) to rederive the probability you found in (a).
Answers
suppose they are independent of a geometric random variable with parameter p. Let M = max(x1,....,xN) (a) Find P{M<} by conditioning on N is nλe^(-nλx)
Given fx (x) = λe^λx
Fx (x) = 1 – e^-λx x…0
To find distribution of Min (X1,….Xn)
By applying the equation
fx1 (x) = [n! / (n – j)! (j – 1)!][F(x)]^j-1[1-F(x)]^n-j f(x)
For minimum j = 1
[Min (X1,…Xn)] = [n!/(n-1)!0!][F(x)]^0[1-(1-e^-λx)]^n-1λe^-λx
= ne^[(n-1) λx] λe^(λx)
= nλe^(-λx[1+n-1])
= nλe^(-nλx)
learn more about of variable here
https://brainly.com/question/6472483
#SPJ4
What is the length of side CB to one decimal place?
B
A
10
53°
C
▸
Answers
The length of side CB to one decimal place is 89.3.
To find the length of side CB in the given triangle, we can use the sine rule. The sine rule states that in a triangle, the ratio of the length of a side to the sine of its opposite angle is constant.
In this case, we have the angle C as 53° and the side opposite to it, side CB, as the unknown. Let's denote the length of side CB as x.
According to the sine rule:
sin(C) / x = sin(A) / AB
We know that angle A is 37° and AB is 120 units. Plugging in the values:
sin(53°) / x = sin(37°) / 120
To find x, we can rearrange the equation:
x = (120 * sin(53°)) / sin(37°)
Calculating this expression gives us:
x ≈ 89.32
Rounding this value to one decimal place, the length of side CB is approximately 89.3.
For more such questions on decimal,click on
https://brainly.com/question/28393353
#SPJ8
When a constant force acts upon an object, the acceleration of the object varies inversely with its mass. When a certain constant force acts upon an object with mass 4kg, the acceleration of the object is 15/ms2. If the same force acts upon another object whose mass is
10kg, what is this object's acceleration?
Answers
Answer:
\(a = 6m/s^2\)
Step-by-step explanation:
Given
When mass = 4kg; Acceleration = 15m/s²
Required
Determine the acceleration when mass = 10kg, provided force is constant;
Represent mass with m and acceleration with a
The question says there's an inverse variation between acceleration and mass; This is represented as thus;
\(a\ \alpha\ \frac{1}{m}\)
Convert variation to equality
\(a = \frac{F}{m}\); Where F is the constant of variation (Force)
Make F the subject of formula;
\(F = ma\)
When mass = 4kg; Acceleration = 15m/s²
\(F = 4 * 15\)
\(F = 60N\)
When mass = 10kg; Substitute 60 for Force
\(F = ma\)
\(60 = 10 * a\)
\(60 = 10a\)
Divide both sides by 10
\(\frac{60}{10} = \frac{10a}{10}\)
\(a = 6m/s^2\)
Hence, the acceleration is \(a = 6m/s^2\)
An automobile purchased for use by the manager of a firm at a price of $32,500 is to be depreciated by using the straight-line method over 5 years. What will be the book value of the automobile at the end of 3 years? (Assume that the scrap value is $0.) $
Answers
The book value of the automobile at the end of 3 years is $13,000.
What is the book value?The straight-line method is method of depreciation that allocates the same depreciation expense each year.
Straight line depreciation expense = (Cost of asset - Salvage value) / useful life
($32,500 - 0) / 5 = $6,500
Total depreciation in 3 years = $6,500 x 3 = $19,500
Book value = cost of the automobile - total depreciation
$32,500 - $19,500 = $13,000
To learn more about straight line depreciation, please check: https://brainly.com/question/6982430
#SPJ1
Mr. Nelson is checking some of the school's sport balls to make sure they are in good shape and
properly inflated. Use the table of recommended air pressures to define the ranges for properly inflated
balls.
Ball
Average recommended psi Tolerance
(pounds per square inch)
Soccer ball 12.05
+3.55
Basketball 8.00
+0.5
I
Volleyball
4.44
+0.18
Part I: Write an absolute value inequality for the recommended air pressure range for each type of ball.
Use the variable x for the ball's actual air pressure. (3 points)
Answers
Answer:
Step-by-step explanation:
Hello!
The variable of interest is
X: air pressures of properly inflated sports balls.
Average recommended psi Tolerance
(pounds per square inch)
Soccer ball 12.05 ±3.55
Basketball 8.00 ±0.5
Volleyball 4.44 ±0.18
Each recommendation is expressed like the "average air pressure" ± "standard deviation of the recommended air pressure" so if you express it in inequality it will be:
X[bar]-S ≤ X ≤ X[bar]+S
So for each ball type, you can write it as:
Soccer ball
12.05-3.55 ≤ X ≤ 12.05+3.55
8.5 ≤ X ≤ 15.6
Basketball
8.00-0.5 ≤ X ≤ 8.00+0.5
7.5 ≤ X ≤ 8.5
Volleyball
4.44-0.18 ≤ X ≤ 4.44+0.18
4.26 ≤ X ≤ 4.62
I hope this helps!
Answer:
Step-by-step explanation:
This is what I got!
Part I:
Soccer ball: | x – 12.05 | ≤ 3.55
Basketball: | x – 8 | ≤ 0.5
Volleyball: | x – 4.44 | ≤ 0.18
Part II:
Basketball: | x – 8 | > 0.5
Part III:
Basketball:
| x – 8 | ≤ 0.5
x – 8 ≤ 0.5
x ≤ 8.5
x – 8 ≥ 0.5
x ≥ 7.5
7.5 ≤ x ≤ 8.5
Howdy! Thanks for stopping by my question! I would really appreciate the help! I've attached the question below. Thanks!
I'd appreciate if you made sure to double check your answers and provide everything the question is asking! INCLUDE ALL STEPS!

Answers
Answer:
a) x = 1 ± (3/7)√7
b) (-∞, -5) ∪ [-2, 5) ∪ [6, ∞)
Step-by-step explanation:
You want solutions to the relations ...
7 +1/x = 1/(x-2)(x² -4x -12)/(x² -25) ≥ 0a) 7 + ...We like to solve these in the form f(x) = 0. It helps avoid extraneous solutions.
\(7+\dfrac{1}{x} -\dfrac{1}{x-2}=0\\\\\\\dfrac{7x+1}{x}-\dfrac{1}{x-2}=0\\\\\\\dfrac{(7x+1)(x-2)-x}{x(x-2)}=0\\\\\\ \dfrac{7x^2-14x-2}{x(x-2)}=0\)
The roots of the numerator quadratic are found by ...
x² -2x -2/7 = 0 . . . . . divide by 7
x² -2x +1 -9/7 = 0 . . . . add and subtract 1
(x -1)² = 9/7 . . . . . . . . . . write as a square, add 9/7
x -1 = ±√(9·7/49) = ±(3/7)√7 . . . . take the square root
x = 1 ± (3/7)√7
b) (x² - ...Rational inequalities are best solved by identifying the roots of numerator and denominator. These tell you where the function changes sign. The end behavior of the rational function tells you what the signs are changing from.
\(\dfrac{x^2-4x-12}{x^2-25}\ge 0\\\\\\\dfrac{(x+2)(x-6)}{(x+5)(x-5)}\ge0\)
This has a horizontal asymptote at y=1 for |x|→∞. It has vertical asymptotes at x=±5.
The sign changes occur at x ∈ {-5, -2, 5, 6}. The rational expression is positive (approaching +1) for x < -5 and for x > 6. It is negative in the adjacent intervals, so positive again for -2 < x < 5.
The inequality is satisfied for ...
x < -5-2 ≤ x < 56 ≤ xDecide whether the relation is a function?

Answers
Answer:
A property of a function is that it gives one output for an input
if a function gives one output for an input, it is a function and otherwise it is not a function otherwise
here, we can see that we have 2 outputs for the input '6'. therefore, it is NOT a function
can someone help me. Tom can wash 44 plates in 3 minutes. How long will tike him to wash 12 plates?
Answers
We can write a proportion.
44:3 = 12:m
~Simplify
44m = 36
~Divide 44 to both sides
m = 36/44 or 9/11 minutes
Best of Luck!
Answer: 0.818 minutes
Step-by-step explanation:
You would normally divide 44/3 to see how many plates are washed per minute, but if you reverse it, 3/44 then you will know how much time is spent washing each plate which is 0.068181. Multiply that by 12 and there’s your answer
What is the value of x

Answers
Temporarily remove base of exponents:
5&5
New equation and subtract to separate x:
x+2=9
-2 -2
x=7
New Equation: 5^7+2=5^9
Answer: X=7
The graph shows the hourly wage requirement m (in dollars) *
for employees in a state. Which inequality represents
the state's hourly wage requirement. (section 2.2)
7.5
8
m≥ $9.5 per hour
m> $9.5 per hour
m≥ $9.25 per hour
m> $9.25 per hour
8.5
9
9.5 10
1 point
Answers
An inequality that represents the state's hourly wage requirement include the following: C. m ≥ $9.25 per hour.
What is an inequality?In Mathematics and Geometry, an inequality simply refers to a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the inequality symbols;
Greater than (>).Less than (<).Greater than or equal to (≥).Less than or equal to (≤).Assuming the variable m represent the state's hourly wage requirement. Additionally, each interval on the number line represent 0.25 per hour.
Since the shaded circle (dot) is located at point 9.25 and the arrows points or increases to the right, an inequality that represents the state's hourly wage requirement is m ≥ $9.25 per hour.
Read more on inequality here: brainly.com/question/27976143
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

If the formula y = r is changed by adding one (shown in red below), what effect would that change have on the function's values? px) = 23+1 Select an answer What effect would it have on the graph? Select an answer
Answers
Given:
\(y=x^3\)\(f(x)=x^3+1\)From the given y = x³, it has changed to f(x) = x³ + 1
Adding a value to the y-intercept of a function will result for its graph to shift upward.
In this case, since we added 1 (+1) to the formula, this will add 1 to all the y values of the graph. Therefore for the first part of the question, the answer would be "It would add one to all the y-values"
Next, since we know that adding a y-intercept will move the graph upwards, the answer for the second part would be "It will shift all points up one."
To make it even more clearer, here is an example.
To conclude this, the answer to the first part would be ""It would add one to all the y-values"
S
the cost of New York Yankees baseball cap is 24.00. The local sporting goods store sells it for $30.00. markup rate
