Given f(x) = 2x² + 8x - 4 and g(x) = 5x +6, find 3f(x) – 2g(x).
Answers
Step-by-step explanation:
When the problem says 3f(x), it means that you are multiplying f(x) by 3. The same goes for 2g(x).
\(3(2x^2+8x-4)= 6x^2+24x-12\)
\(2(5x+6) = 10x+12\)
Now, we subtract f(x) from g(x) after being multiplied.
\((6x^2+24x-12)-(10x+12)\)
\(6x^2+14x-24\)
Related Questions
The graph of f*x)=2^(x+3) shifts 10 units to the right when it is replaced with the graph of f(x)=2^(x-k). What is the value of k?
Answers
Answer:
7
Step-by-step explanation:
f(x) = 2^(x + 3)
Shifted 10 units to the right:
f(x) = 2^(x + 3 − 10)
f(x) = 2^(x − 7)
Therefore, k = 7.
Write the following expression using the fewest possible terms. (−4x − 15) + (17 + 7x)
Answers
Answer:
3x +2
Step-by-step explanation:
Write the following expression using the fewest possible terms.
(−4x − 15) + (17 + 7x) =
-4x -15 + 17 + 7x=
3x +2
PLEASE HELP I WILL MARK YOU BRAINIEST

Answers
Answer:
x greater than or equal to 1/3
Step-by-step explanation:
Answer:
equation is unclear. Send another pic.
1. Use the elimination strategy to solve this linear system:
(1) 12c + 28d = 12 (2) -20c + 16d = 168
2. Determine the number of solutions of this linear system:
(1) 7x − 3y = 43 (2) 7x - 3y = 13
Answers
The solution to the linear system is c = -6 and d = 3.
To solve the linear system using the elimination strategy, we can eliminate one variable by adding or subtracting the equations. Let's solve the first linear system:
(1) 12c + 28d = 12
(2) -20c + 16d = 168
To eliminate one variable, we can multiply equation (1) by 5 and equation (2) by 3, which will result in opposite coefficients for 'c'. This will allow us to eliminate 'c' when adding the equations together:
(1) 60c + 140d = 60
(2) -60c + 48d = 504
Now, we can add the equations:
(60c + 140d) + (-60c + 48d) = 60 + 504
188d = 564
d = 564/188
d = 3
Substituting the value of 'd' back into equation (1):
12c + 28(3) = 12
12c + 84 = 12
12c = 12 - 84
12c = -72
c = -72/12
c = -6
The solution to the linear system is c = -6 and d = 3.
Now let's analyze the second linear system:
(1) 7x - 3y = 43
(2) 7x - 3y = 13
By comparing the two equations, we can see that they have the same coefficients for both 'x' and 'y', and the constant terms on the right side are different. This means the lines represented by the equations are parallel and will never intersect.
The linear system has no solution.
For more questions on linear system
https://brainly.com/question/2030026
#SPJ8
HELP ME PLS THANK YOU<333

Answers
Answer:
d
Step-by-step explanation:
edge 2020
p.s. pls mark brainliest, and have a good day! :)
What percent of 2 is 32? If necessary, round your answer to the nearest tenth.
Answers
Answer:
Below
Step-by-step explanation:
32/2 x 100% = 1600 %
Complete the ratio table of the median price of renting a two-bedroom apartment by finding the value of x and y. Round answers to two decimal places. Norfolk $951 Richmond $1,042 1 X Х 100 у To solve the values set up and solve a a. Bar Chart b. Ratio c. Proportion d. Weighted Average x = y =
Answers
2+4=6 is true
7*8=56 is true
So the statement 2+4=6 AND 7*8=56 is also true
So the answer for question #36 is a) the statement is true because both proporsitions are true
I have a large money box, about 10 inches wide and 5 inches tall. Roughly, how many coins can I place in my empty money box?"
Answers
Answer:
Overall, it depends what type of coin you are using because each ones size is different. Or, if you are referring to the riddle it will be just one coin.
The correct answer is approximately 3,968 coins can be placed in the empty money box based on estimation. Based on these calculations, you can roughly estimate a volume calculation that place around 7936 coins in your empty money box, assuming the coins are similar in size to a quarter.
To estimate the number of coins that can fit in your money box, we need to consider the volume of the box and the volume of a single coin.
Calculate the volume of the money box:
Volume = Length * Width * Height
Volume = 10 inches * 10 inches * 5 inches
Volume = 500 cubic inches
Estimate the volume of a single coin. Let's assume a common coin, such as a quarter:
Diameter of a quarter ≈ 0.96 inches
Thickness of a quarter ≈ 0.07 inches
Volume of a coin ≈ π * (\(radius^2\)) * thickness
Volume of a quarter ≈\(3.14 * (0.48) ^2 * 0.07\)inches
Volume of a quarter ≈ 0.063 cubic inches
Calculate the number of coins that can fit in the money box:
Number of coins ≈ Volume of the money box / Volume of a coin
Number of coins ≈ 500 cubic inches / 0.063 cubic inches
Number of coins ≈ 7936 coins (approximately)
Therefore, approximately 3,968 coins can be placed in the empty money box based on estimation. Based on these calculations, you can roughly estimate a volume calculation that place around 7936 coins in your empty money box, assuming the coins are similar in size to a quarter.
Learn more about volume and estimations here:
https://brainly.com/question/20664459
#SPJ2
can someone help me on number 4

Answers
Answer:
\(P = 48 in\),\(A= 120in^2\)
Step-by-step explanation:
Again we can use Pythagorean theorem to find the missing side
x^2 + 15^2 = 17^2
x^2 + 225 = 289
Subtract 225 from both sides
x^2 = 64
Find the square root of both sides
√x^2 = √64
x = 8
So
l = 15in, w = 8in
P=2(15) + 2(8)
P = 30 + 18
P = 48 in
A= 15(8)
A= 120in^2
Please help i’ll rate brainliest too

Answers
Answer:
- 4
Step-by-step explanation:
h(x) = sin x
f(x) = | 3x - 4 |
g(x) = 2x² - 6
h( \(\frac{\pi }{2}\) ) = sin ( \(\frac{\pi }{2}\) ) = 1
f ( 1 ) = | 3 × 1 - 4 | = 1
g ( 1 ) = 2( 1² ) - 6 = - 4
g ( f ( h ( \(\frac{\pi }{2}\) ) ) ) = - 4
What’s the area? For this

Answers
Answer: 460.61
Step-by-step explanation:
4. Suppose y varies directly with x. If y = 6 when x = -2, find x when y = 15.
Answers
Answer:
x is -7.5 or -14/2 or -7½
Step-by-step explanation:
- Supposing y varies directly with x
\( { \tt{y \: \alpha \: x}} \\ \: \: \: \: { \tt{y = kx}} \)
[k is a constant of proportionality (k ≠ 0)]
- When y is 6, x is -2
\( \: \: \: \: \: \: \: \: \: { \tt{6 = (k \times ^{ - }2) }} \\ { \tt{6 = - 2k}} \\ { \tt{k = - 3 \: \: }}\)
- Therefore, the equation is;
\({ \boxed{ \tt{y = - 2x}}}\)
- What is x when y is 15
\({ \tt{15 = - 2x}} \\ { \tt{x = - 7.5}}\)
The value of x is -5
The equation for a direct variation is y = kx, where k is the constant of variation. Since we know that y = 6 when x = -2, we can solve for k:
k = y/x
k = 6/-2
k = -3
Therefore, the equation for this direct variation is y = -3x. To find x when y = 15, Substitute k = -3 and y = 15 into the equation
15 = -3x
Then solve x,
x = \(\frac{-15}{3}\)
x = -5
Therefore, when y = 15, x = -5.
Learn how to solve equation:
brainly.com/question/26260688
What does 15+5= 18 +
Answers
Answer:
2
Step-by-step explanation:
Answer: 20
Step-by-step explanation:
Consider a Poisson probability distribution with λ = 5.1. Determine the following probabilities.
a) exactly 5 occurrences
b) more than 6 occurrences
c) 3 or fewer occurrences
Click the icon to view a partial table of Poisson probabilities.
a) The probability of exactly 5 occurrences is
(Round to four decimal places as needed.)
Answers
The probability of exactly 5 occurrences is (Rounding to three Decimal places), we get P(X ≤ 3) ≈ 0.251.
a) The probability of exactly 5 occurrences is given by the Poisson probability mass function:
P(X = 5) = (e^(-λ) * λ^5) / 5! = (e^(-5.1) * 5.1^5) / 120 ≈ 0.1755
Rounding to four decimal places, we get P(X = 5) ≈ 0.1755.
b) The probability of more than 6 occurrences can be calculated as the complement of the probability of 6 or fewer occurrences:
P(X > 6) = 1 - P(X ≤ 6) = 1 - (P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6))
Using the Poisson probability mass function and the given value of λ, we can calculate each of the probabilities:
P(X = 0) ≈ 0.006
P(X = 1) ≈ 0.031
P(X = 2) ≈ 0.079
P(X = 3) ≈ 0.135
P(X = 4) ≈ 0.174
P(X = 5) ≈ 0.1755
P(X = 6) ≈ 0.1493
Substituting these values into the formula, we get:
P(X > 6) ≈ 1 - (0.006 + 0.031 + 0.079 + 0.135 + 0.174 + 0.1755 + 0.1493) ≈ 0.249
Rounding to three decimal places, we get P(X > 6) ≈ 0.249.
c) The probability of 3 or fewer occurrences is given by the cumulative distribution function:
P(X ≤ 3) = ∑ P(X = k), for k = 0, 1, 2, 3.
Using the Poisson probability mass function and the given value of λ, we can calculate each of the probabilities:
P(X = 0) ≈ 0.006
P(X = 1) ≈ 0.031
P(X = 2) ≈ 0.079
P(X = 3) ≈ 0.135
Adding these probabilities, we get: P(X ≤ 3) ≈ 0.251
Rounding to three decimal places, we get P(X ≤ 3) ≈ 0.251.
To know more about probability
https://brainly.com/question/24756209 .
#SPJ11
Write the slope-intercept form of the equation for each line.

Answers
Step-by-step explanation:
points on the line: (4, -2) & (-5, 3)
gradient of the line = -5/9
general equation for all straight lines: y = mx + c
substitute one coordinate and the gradient into the equation. 3 = (-5/9)(-5) + c
therefore, c = 2/9
so the general equation is y = (-5/9)x + 2/9
< Question 8 of 42
Macmillan Learning
>
Arrange the given numbers from largest to smallest.
Largest
0.51
7.6
10²
5.6
105
4.9
10-3
Smallest
Answer Bank
Answers
From the given numbers ,The order from largest to smallest is 105,100,7.6,5.6,4.9,0.51,0.001
What is Descending order?
Descending order can be defined in such a way that the order is from largest to smallest.
Given numbers are ,
0.51 , 7.6 , 10^2 , 5.6 , 105 , 4.9 , 10^-3
10^2 = 10*10 = 100 .
so a^m = a multiplied by m times .
a^-m = 1/ a^m.
10^-3 = 1/1000 = 0.001
So,
We have to write from largest to smallest
we get,
105,100,7.6,5.6,4.9,0.51,0.001
Hence, From the given numbers ,The order from largest to smallest is 105,100,7.6,5.6,4.9,0.51,0.001
To learn more about Descending order from the given link.
https://brainly.com/question/23938305
#SPJ1
When this net is folded into a cube, which
edge joins with edge X?
X
F
A
E
B
D
C
Answers
When edge D connects with edge X, this net is folded into a cube, which is obtained by folding the given figure in cube.
Explain about the cube?A cube is a solid shape with six square faces. Each side of a square has the same side length, so all faces are the same size.
A cube has 12 sides and 8 vertices. Each vertex refers to the angle where the three edges of the cube meet.
Shape Properties of Cube
It is a three-dimensional square shape It has 6 faces, 12 sides and 8 vertices All faces are square All sides are of equal length Every vertex meets three faces and three sides Sides are square All sides are of equal length Each vertex meets three faces and three sides parallel to it All angles of a cube are right anglesThus, when edge D connects with edge X, this net is folded into a cube.
Know more about the cube
https://brainly.com/question/19891526
#SPJ1

Six less than twice a number x is four
Answers
Answer:
2 x − 6
Explanation:
"Six less than.." means "Subtract 6 from".
Do not confuse this with "Six less..." which means "Subtract from 6".
Confusing, I know.
We know that "Double a number" means
2 x , where x is your mystery number.
Therefore, we have:
2 x − 6 , which translates to "6 less than 2x" or "6 less than twice a number"
A fish is reeled in at a rate of 1.9 feet per second from a point 10 feet above the water (see figure). At what rate is the angle between the line and the water changing when there is a total of 25 feet of line out?
Answers
9514 1404 393
Answer:
1.9 degrees per second
Step-by-step explanation:
The angle α the line makes with the water can be described by ...
Sin = Opposite/Hypotenuse
sin(α) = 10/(25 -1.9t)
Taking derivatives gives ...
α'·cos(α) = -10(-1.9)/(25 -1.9t)²
Then the rate of change of the angle at t=0 is ...
α' = 19/(25²·cos(α))
Of course, cos(α) = √(1 -sin(α)²) = √(1 -(10/25)²) = √(21/25), so we have ...
α' = 19/(125√21) . . . radians/second
α' ≈ 0.033269 radians/s ≈ 1.90 degrees/s
The prior probabilities for events
A1, A2, and A3
are
P(A1) = 0.20,
P(A2) = 0.30,
and
P(A3) = 0.50.
The conditional probabilities of event B given
A1,
A2,
and
A3
are
P(B | A1) = 0.50,
P(B | A2) = 0.30,
and
P(B | A3) = 0.40.
(Assume that
A1, A2, and A3
are mutually exclusive events whose union is the entire sample space.)
(a)
Compute
P(B ∩ A1), P(B ∩ A2), and P(B ∩ A3).
P(B ∩ A1)
=
P(B ∩ A2)
=
P(B ∩ A3)
=
(b)
Apply Bayes' theorem,
P(Ai | B) = P(Ai)P(B | Ai)
P(A1)P(B | A1) + P(A2)P(B | A2) + + P(An)P(B | An),
to compute the posterior probability
P(A2 | B).
(Round your answer to two decimal places.)
(c)
Use the tabular approach to applying Bayes' theorem to compute
P(A1 | B),
P(A2 | B),
and
P(A3 | B).
(Round your answers to two decimal places.)
Events P(Ai)
P(B | Ai)
P(Ai ∩ B)
P(Ai | B)
A1
0.20 0.50 A2
0.30 0.30 A3
0.50 0.40 1.00 1.00
Answers
(a) Through the conditional probability formula:\(P(B ∩ A) = P(B | A) P(A),\)
\(P(B / A1) P(A1) = 0.50 x 0.20 = 0.10A2 = 0.30 x 0.30 = 0.09A3= 0.40 x 0.50 = 0.20\)
(b)Bayes' theorem gives
\(P(A2 | B) = p(B | A2) p(A2) / [p(B | A1) P(A1) + p(B | A2) P(A2) + p(B | A3) p(A3)]= 0.26Thus, P(A2 | B) = 0.26.\)
(c)the tabular approach can show us
Events P(Ai) P(B | Ai) P(Ai ∩ B) P(Ai | B)
A1 0.2 0.5 0.1 0.167
A2 0.3 0.3 0.09 0.307
A3 0.5 0.4 0.2 0.526
Therefore,\(P(A1 | B) = 0.167, p(A2 | B) = 0.307, p(A3 | B) = 0.526.\)
To know more about probabilities
brainly.com/question/30034780
#SPJ4
What is the approximate surface area of the Hayden Sphere in terms of T?
4731 ft?
37857 ft?
75697 ft2
18927 ft?

Answers
Answer:
\(A=7569\pi \ ft^2\)
Step-by-step explanation:
The diameter of a sphere is 87 feet.
We need to find its surface area. The formula for surface area is given by :
\(A=4\pi r^2\)
Where
r is the radius of the sphere
\(A=4\pi \times (\dfrac{87}{2})^2\\\\=7569\pi \ ft^2\)
So, the surface area of the sphere is equal to \(7569\pi \ ft^2\).
solve the equation -16=a- 19
Answers
Answer:
a = 3
Step-by-step explanation:
Collect like-terms:
\( - 16 = a - 19\)
\(a = - 16 + 19\)
\(a = 3\)
Answer: 3
Step-by-step explanation: you take 19 from 3 giving you -16
What is the length of EF in the right triangle below?
D
26
10
E
F
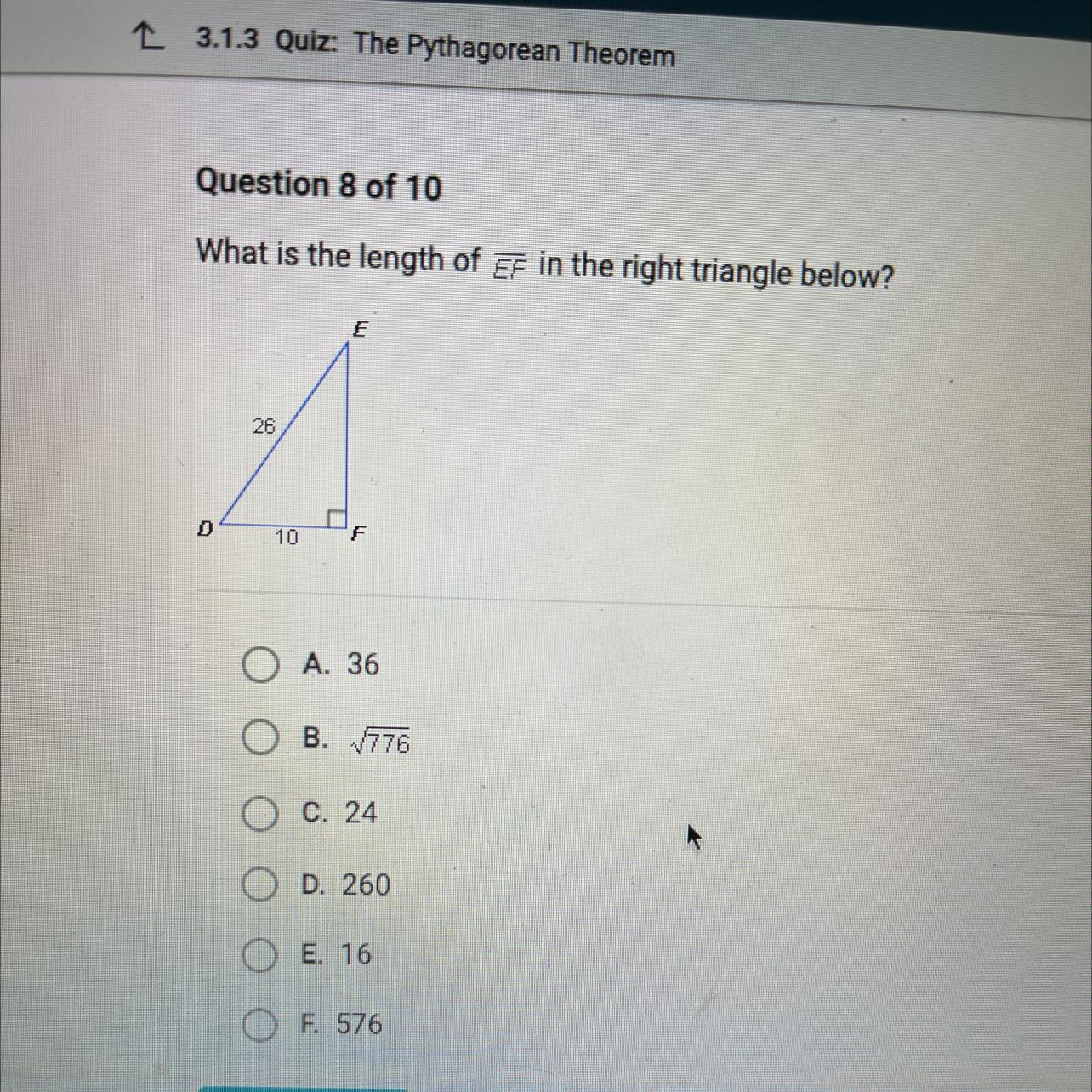
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
5+2÷4-2=
pls do this u dont have to do the work
Answers
Answer:
3.5
Step-by-step explanation:
Order of operations
45 points!!!
solve questions 10-11

Answers
Answer:
1 Question: D
2 Question: C
Just Imo. I did the work tho.
graph y = 6/5x - 6/5
Answers
The ordered pairs are (1,0), (2,6/5),(3,12/5)
What is the solution to a linear equation?The solution of a linear equation is defined as the points, in which the lines represent the intersection of two linear equations. In other words, the solution set of the system of linear equations is the set of all possible values to the variables that satisfies the given linear equation.
Given here: The equation as y = 6x/5 - 6/5
putting (1,0) in the equation we get 6×1/5-6/5=0
Similarly we can find the ordered pair as y = 6/5x - 6/5
Hence, The ordered pairs are (1,0), (2,6/5),(3,12/5)
Learn more about linear equation here:
brainly.com/question/545403
#SPJ1
Suppose the true proportion of voters in the county who support a specific candidate is 0.38. Consider the sampling distribution for the proportion of supporters with sample size n = 168.
What is the mean of this distribution?
0.38
Correct
What is the standard error of this distribution?
Answers
Using the Central Limit Theorem, it is found that:
The mean is of 0.38.The standard error is of 0.0374.What does the Central Limit Theorem states about the sampling distribution of sample proportions?It states that for a proportion p in a sample of size n, the sampling distribution of sample proportion is approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1 - p)}{n}}\), as long as \(np \geq 10\) and \(n(1 - p) \geq 10\).
The estimate and the sample size are given by:
p = 0.38, n = 168.
Hence the mean is given by:
\(\mu = p = 0.38\)
The standard error is given by:
\(s = \sqrt{\frac{p(1 - p)}{n}} = \sqrt{\frac{0.38(0.62)}{168}} = 0.0374\)
More can be learned about the Central Limit Theorem at https://brainly.com/question/16695444
#SPJ1
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
what is -5/12 x 8/13 in its simplest form
Answers
Answer:
-10/39
Step-by-step explanation:
I Think that thats the anwser i hope this helps.
find the slope and y-intercept.
Answers
The slope and the y-intercept of the line y = 4x + 5 are given as follows:
Slope of 4.y-intercept of 4.How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
The coefficients m and b represent the slope and the intercept, respectively, and are explained as follows:
m represents the slope of the function, which is by how much the dependent variable y increases or decreases when the independent variable x is added by one.b represents the y-intercept of the function, representing the numeric value of the function when the input variable x has a value of 0. On a graph, the intercept is given by the value of y at which the graph crosses or touches the y-axis.The function for this problem is given as follows:
y = 4x + 5.
Hence the slope and the intercept are given as follows:
m = 4.b = 5.Missing InformationThe problem asks for the slope and the intercept of y = 4x + 5.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1