given g(x) = -x - 4, find g(-2)
Answers
Answer: -2
Step-by-step explanation:
\(g(x) = g(-2) = -(-2)-4=2-4=-2\)
Related Questions
Share your own multi-step combination problem
Answers
My own multi-step combination problem is given below:
Amanda was planning a dinner party for 10 people, and she want to choose a menu of 3 fruit , 2 meat pie, and 2 desserts. Amanda have a total of 5 fruit , 4 meat pie, and 3 desserts to choose from. How many different dinner menus can Amanda create?How do you solve the multi-step combination?To solve this problem, Amanda need to use the formula for combinations and it is:
nCr = n! / (r! x (n-r)!)
where:
n = total number of items to select from
r is the number of items to select.
First, we have to calculate the number of ways to select 3 fruit from 5, hence it will be:
5C3
= 5! / (3! x (5-3)!)
= 10
Next, we have to calculate the number of ways to select 2 meatpie from 4 and it will be
4C2
= 4! / (2! x (4-2)!)
= 6
Lastly,, we need to calculate the number of ways to select 2 desserts from 3 and it will be:
3C2
= 3! / (2! x (3-2)!)
= 3
To have the total number of dinner menus, we have to multiply these three numbers together:
= 10 x 6 x 3
= 180
Therefore, one can say that Amanda have 180 different dinner menus that she can be create.
Learn more about multi-step combination from
https://brainly.com/question/2191693
#SPJ1
Round off 1,296,717 to 3 significant figures
Answers
Answer:6 1296720 1.29672 × 106
5 1296700 1.2967 × 106
4 1297000 1.297 × 106
3 1300000 1.30 × 106
2 1300000 1.3 × 106
1 1000000 1 × 106
Step-by-step explanation:
Find the slope of the line that passes through all of the points
on the table.
X
2
7
12
17
y
2
-3
-8
-13
Only need the answer

Answers
Answer:
Step-by-step explanation:
so first you need to find the slope
you can draw the line on a graph and use a protractor
final answer=46 degrees
Answer:-5/-19
the answer is -5/-19 and can not be simplify
A vending machine automatically pours soft drinks into cups. The amount of soft drink dispensed into a cup is normally distributed with a mean of 7.5 ounces and standard deviation of 0.5 ounces. Examine the figure below and answer the following questions.
a.) Estimate the probability that the machine will overflow an 8-ounce cup. (Round your answer to two decimal places.)
b.) Estimate the probability that the machine will not overflow an 8-ounce cup. (Round your answer to two decimal places.)
c.) The machine has just been loaded with 300 cups. How many of these do you expect will overflow when served?

Answers
The machine has just been loaded with 850 cups. How many of these do you expect will overflow when served?
0.1587*850 = 134.857..
How to solveA vending machine automatically pours soft drinks into cups.
The amount of soft drink dispensed into a cup is normally distributed with a mean of 7.6oz and a standard deviation of 0.4oz.
Examine figure 7.- and answer the following questions.
a) estimate the probability that the machine will overflow an 8oz cup.
Procedure:
Determine the z-score for 8
z(8) = (8-7.6)/0.4 = 0.4/0.4 = 1
P(x>8) = P(z>1) = 0.1587..
-----------------------
b) Estimate the probability that the machine will not overflow an 8oz cup.
P(z<1) = 1 - 0.1587 = 0.8413..
-----------------
c) the machine has just been loaded with 850 cups. How many of these do you expect will overflow when served?
0.1587*850 = 134.857..; Rounded down you get 134 cups
Read more about probability here:
https://brainly.com/question/24756209
#SPJ1
PLEASE I NEED ANSWERS ASAP
1. Find the missing coordinate given m = -5 and goes through the points (x, 3) and (5, -7). Show your work.
2. Identify the slope in the equation 9x + 2y = -7. Show your work.
Answers
The required solution for the coordinate and the slope of the line, 1. missing coordinate is 2. Slope of the line 9x + 2y = -7 is m = -9/2
Here,
1.
Standard equation of the line,
y = mx + c
From the given, we have m = -5 and a point (5,- 7)
Now,
-7 = -5 * 5 + c
c = -7 + 25
c = 18
equation become
y = -5x + 18
Now putting y = 3
3 = -5x + 18
-15 = -5x
x = 3
So the required missing coordinate is (3, 3)
2.
Slope of equation 9x + 2y = -7
9x + 2y = -7
y = -9/2 -7/2
The coefficient of x is the slope of the equation. So,
m = --9/2
Thus, the required solution for the following problem of the line,
1. missing coordinate is
2. Slope of the line 9x + 2y = -7 is m = -9/2.
Learn more about slopes here:
https://brainly.com/question/3605446
#SPJ1
math mat mhaha ha hbahuh gyahy w guabhbhabhabhnahqnhuabuha vha ya yva cyvvahba cya yva buabbyga hay avu aygabyga ygabgyagyabhyabga ahh abbahhajna buiajaj
qhubuag qjjbbaqbjbqhuqguqbqbqyqbyqbyqb math help

Answers
So, we know that JI and JX are perpendicular (first statement). That just means that they mean at an angle of 90*.
That means CIJ has an angle of 150*-90*=60*. Therefore, as IG bisects CIJ , both CIG and GIJ have angle 60*/2=30*.
Half a circle has 180*. GIR is just short of CIG to be a half circle.
Therefore
180*-mCIG=mGIR
We know mCIG was 30*, so
150*=mGIR
7. Marie can make 12 small mango pies for every 10 mangoes. How many pie
A. Marie can make 30 pies.
C. Marie can make 50 pies
B. Marie can make 40 pies.
D. Marie can make 60 pies
sorry putol po kasi eto
Answers
Answer:
D. Marie can make 60 pies.
Step-by-step explanation:
In this problem, we know that amount of small mango pies is directly proportional to the amount of mangoes. The amount needed for preparing an amount of pies is calculated by simple rule of three:
A. Marie can make 30 pies.
\(x = \frac{10\,mangoes}{12\,pies}\times 30\,pies\)
\(x = 25\,mangoes\)
25 mangoes are required for producing 30 pies.
B. Marie can make 40 pies.
\(x = \frac{10\,mangoes}{12\,pies}\times 40\,pies\)
\(x = 33.333\,mangoes\)
34 mangoes are required for producing 40 pies.
C. Marie can make 50 pies.
\(x = \frac{10\,mangoes}{12\,pies}\times 50\,pies\)
\(x = 41.667\,mangoes\)
42 mangoes are required for producing 50 pies.
D. Marie can make 60 pies.
\(x= \frac{10\,mangoes}{12\,pies}\times 60\,pies\)
\(x = 50\,mangoes\)
50 mangoes are required for producing 60 pies.
The complete statement is: Marie can make 12 small mango pies for every 10 mangoes.How many pies can she make with 50 mangoes.
Hence, correct answer is D.
Mr Noris wrote a doubles fact. It has a sum greater than 6. The number that he added are each less than 6. What fact might he have written?
Answers
9514 1404 393
Answer:
4 + 4 = 8
5 + 5 = 10
Step-by-step explanation:
If we assume Mr Noris restricted himself to integer facts, we require both ...
2n > 6
n < 6
Dividing the first inequality by 2 gives ...
n > 3
Writing the two inequalities as a compound inequality, we have ...
3 < n < 6
There are two integers that satisfy this requirement:
n = 4 or n = 5
So, the doubles fact could have been either of ...
4 + 4 = 8
5 + 5 = 10
Given f(x)=x^2+6x and g(x)=4 x^2, find fg. fg(x)=
Answers
The composite function f·g(x) is 4x⁴+24x³.
The given functions are f(x)=x²+6x and g(x)=4x².
We need to find f·g(x).
We know that, f·g(x)=f(x)×g(x)
Here, f·g(x)=(x²+6x)×4x²
= x²×4x²+6x×4x²
= 4x⁴+24x³
Therefore, the composite function f·g(x) is 4x⁴+24x³.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
1. 3 apples cost $1.26. How much does 1 apple cost?
Answers
Answer:
=$0.42
Step-by-step explanation:
Divide 1.26 by 3 and you'll get $0.42
Hope this helps (:
A member of the sales team earns $10,000 a year as a base salary and 6% commission on sales. A team member made sales totaling $520,000 last year. What was the team member's total pay for the year, including base salary and commission from the sales? screenshot the picture and answer it on the picture and then use it as answer or don't and just answer

Answers
Answer:
41200
Step-by-step explanation:
Evaluate the double integral ∬R(3x−y)dA, where R is the region in the first quadrant enclosed by the circle x2+y2=16 and the lines x=0 and y=x, by changing to polar coordinates.
Answers
Answer:
\(\displaystyle 64-32\sqrt{2}+\frac{32\sqrt{2}}{3}\approx3.66\)
Step-by-step explanation:
\(\displaystyle \iint_R(3x-y)\,dA\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0(3r\cos\theta-r\sin\theta)\,r\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0(3r^2\cos\theta-r^2\sin\theta)\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0r^2(3\cos\theta-\sin\theta)\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\frac{64}{3}(3\cos\theta-\sin\theta)\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\biggr(64\cos\theta-\frac{64}{3}\sin\theta\biggr)\,d\theta\)
\(\displaystyle =\biggr(64\sin\theta+\frac{64}{3}\cos\theta\biggr)\biggr|^\frac{\pi}{2}_\frac{\pi}{4}\\\\=\biggr(64\sin\frac{\pi}{2}+\frac{64}{3}\cos\frac{\pi}{2}\biggr)-\biggr(64\sin\frac{\pi}{4}+\frac{64}{3}\cos\frac{\pi}{4}\biggr)\\\\=64-\biggr(64\cdot{\frac{\sqrt{2}}{2}}+\frac{64}{3}\cdot{\frac{\sqrt{2}}{2}}\biggr)\\\\=64-32\sqrt{2}+\frac{32\sqrt{2}}{3}\biggr\\\\\approx3.66\)
Solve for x.
2x-1+12=6x+3
Answers
Answer:
es pepo cumbia
o PVP TU PON LA SALA Y YO LA HUMILLACIÓN
Answer:
2x-1+12=6x+3
X = 2
Explain:
2x-1+12=6x+3
2x+11+6x+3
( 2x+11 )+(-11-6x)=(6x + 3) + (-11 - 6x)
so that means
X=2
The diagonal BD cuts the quadrilateral
ABCD into a right triangle, ABD, and an
equilateral triangle BCD. The dimensions are
given in inches. How many inches long is
DC?
Hint: Equilateral triangles have three equal
sides

Answers
Answer:
answer is 13 inch.,
Step-by-step explanation:
BCD is equilateral triangle so all side is equal.
and ABD is right angled triangle so. use pythagoras theorem.
BD = 13 inch then DC also 13 inch
Use the graph of g(x) to answer the following question.
The graph of g(x) is a translation of f(x) = x^2
Write the equation for g(x) in vertex form.

Answers
The graph of the translated function is g ( x ) = ( x + 5 )² + 2
Given data ,
Let the parent function be represented as f ( x )
Now , the value of f ( x ) is
f ( x ) = x²
On simplifying , we get
The function is translated 5 units to the horizontal left direction:
And , when the function is translated 2 units in the vertical upward direction:
So , the translated function is
g ( x ) = ( x + 5 )² + 2
Now , the vertex of the function g ( x ) = ( x + 5 )² + 2 is (-5, 2)
Hence , the graph of the function is plotted and g ( x ) = ( x + 5 )² + 2
To learn more about translations click :
https://brainly.com/question/19007400
#SPJ1

Transformations, Graphs, and Diagrams:
1) For the function () = −2 ) !
".$(&'() * + 4:
a) State the following information:
= _____ = _____ = _____ = _____ [2]
b) State any asymptotes. [1]
c) Sketch the transformed function () = −2 ) !
".$(&'() * + 4 , including table of key
points with transformations. In you graph clearly state the points and asymptote(s).
[3]
(
!
" + , + ,
d) Correctly state the domain and range of the function () sketched above.
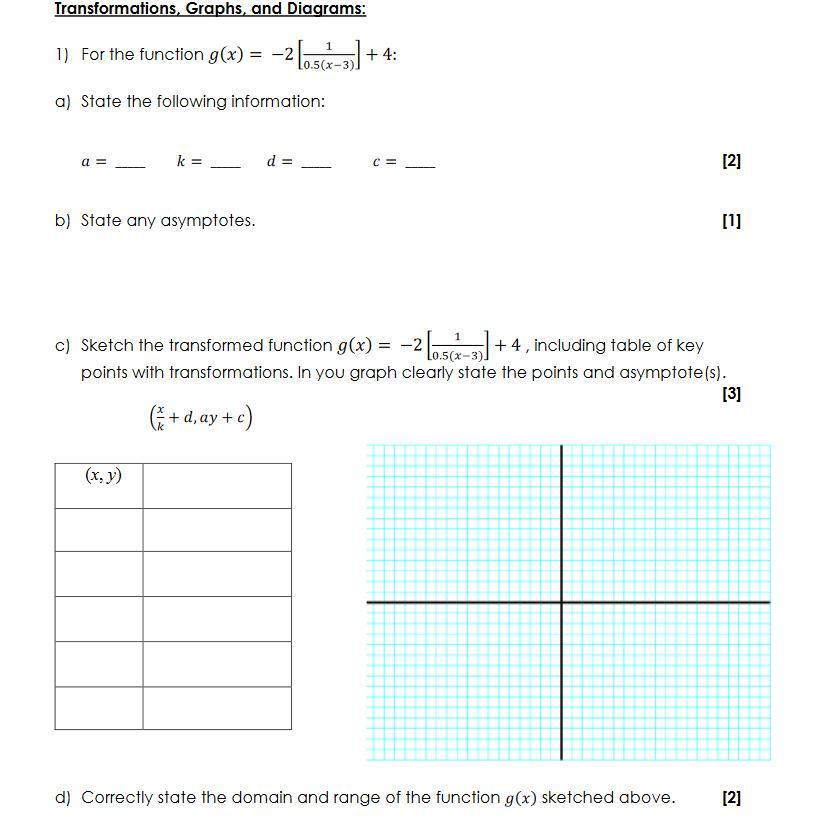
Answers
The asymptotes of the reciprocal function are x = 3 and y = 4. Also, the domain is x < 3 or x > 3 and the range is y < 4 or y > 4
How to determine the values of a, c, d and k?The function is given as:
f(x) = -2[1/0.5(x -3)] + 4
A reciprocal function is generally represented as:
f(x) = a[1/(x -c)] + k
So, we have:
a = -2
c = -3 * 0.5
c = -1.5
k = 4
d = 0
Hence, the values of a, c, d and k are -2, -1.5, 0 and 4
The asymptotesWe have:
f(x) = -2[1/0.5(x -3)] + 4
Set the radical to 0
y = 0 + 4
Evaluate
y = 4
Set the denominator to 0
x - 3 = 0
Evaluate
x = 3
Hence, the asymptotes are x = 3 and y = 4
The graph of the functionSee attachment for the graph of the function f(x) = -2[1/0.5(x -3)] + 4
The table of values is
x y
-4 4.6
-2 4.8
2 8
4 0
From the graph of the function, the domain is x < 3 or x > 3 and the range is y < 4 or y > 4
Read more about functions at:
brainly.com/question/2328150
#SPJ1

What is the surface area of this rectangular prism i-ready

Answers
Answer:
290 in²
Step-by-step explanation:
Using the net of the box given, we can see that there are 4 equal rectangles and 2 equal squares that make up the prism.
Area of the 4 rectangles = 4(60) = 240 in²
Area of the 2 squares = 2(25) = 50 in²
Therefore,
Surface Area of the prism = 240 + 50 = 290 in²
Answer:
The surface area of this prism is 290(in)²
Step-by-step explanation:
The surface area of a box is equal to the sum of the areas of each side of the box.
\(2 \times (lenght) \times (widht) + 2 \times (lenght) \times (height) + 2 \times (widht) \times (height)\)
Substitute the values of the length l=5, the width w=5, and the height h=12 into the formula.
\(2 \times 5 \times 5 + 2 \times 5 \times 12 + 2 \times 5 \times 12\)
Simplify each term.
\(50 + 120 + 120\)
Simplify by adding numbers.
\(290(in)^{2} \)
Hence, The surface area of this rectangular prism is 290in².
Triangle D has been dilated to create triangle D′. Use the image to answer the question.
image of a triangle labeled D with side lengths of 18, 24, and 30 and a second triangle labeled D prime with side lengths of 6, 8, and 10
Determine the scale factor used.
Scale factor of one third
Scale factor of 3
Scale factor of 4
Scale factor of one fourth
Answers
The scale factor used to dilate triangle D to create triangle D' is 1/3. This means that each side length in triangle D' is one-third of the corresponding side length in triangle D.
To determine the scale factor used to dilate triangle D to create triangle D', we can compare the corresponding side lengths of the two triangles.
In triangle D, the side lengths are given as 18, 24, and 30. In triangle D', the corresponding side lengths are given as 6, 8, and 10.
To find the scale factor, we can divide the corresponding side lengths of D' by the corresponding side lengths of D.
Scale factor = Length of corresponding side in D' / Length of corresponding side in D
For the corresponding sides, we have:
Scale factor = 6/18 = 1/3
Please note that the scale factor can also be determined by comparing the area or perimeter of the two triangles. However, in this case, we used the corresponding side lengths to find the scale factor.
For more such questions on corresponding side
https://brainly.com/question/29071853
#SPJ8
parallel lines are two lines that never meet. find an example that contradicts this definition. How would you change the definition to make it more accurate?
Answers
A more modern explanation would be, "Parallel lines are two lines within a given plane that never intersect."
Two lines on a sphere are an illustration that defies the notion of parallel lines. Meridians are the name given to longitude lines on spheres like the Earth.
Meridians are lines that run parallel to one another from the North Pole to the South Pole. However, if we take into account two meridian lines, they will cross at the North and South Poles. Two lines that are originally parallel will, therefore, eventually intersect at the poles on a sphere, defying the notion of parallel lines.
We can change the original definition of parallel lines to read, "Parallel lines are two lines that do not intersect within a given plane."
This adjustment accounts for the fact that lines can exist in many geometrical contexts, such as on a sphere or in three-dimensional space, where the idea of parallelism may be different. By including the phrase "within a given plane," we restrict the concept to the typical geometry seen in Euclidean geometry, where parallel lines do not meet.
A newer definition may therefore read, "Parallel lines are two lines within a given plane that never intersect." This updated definition makes clear that parallel lines must be taken into account inside a certain plane in order to maintain their validity, while also acknowledging the limitations of the idea.
For more such questions on Parallel lines visit:
https://brainly.com/question/30097515
#SPJ8
Determine which set of side measurements could be used to form a right triangle. 6, 4, 8 4, 13, 15 16, 8, 18 6, 8, 10
Answers
The set of side measurements that could be used to form a right triangle is
6, 8, 10How to find the set of sides that can form a right triangleThe problem is solved using the Pythagoras theorem is applicable to right triangle.
the formula of the theorem is
hypotenuse² = opposite² + adjacent²
the set of sides that adheres to this theorem can form a right triangle
plugging the values as in the problem 6, 8, 10
say side 10 = x
x² = 6² + 8²
x² = 36 + 64
x² = 100
x = √100
x = 10
Learn more on Pythagoras theorem here:
https://brainly.com/question/29241066
#SPJ1
It costs $350 to spend 4 nights at the Econo Motel. It costs $475 to spend 6 nights at the Bluebird Inn. Which of these statements is true?
Answers
Answer: A
Step-by-step explanation: The bluebird Inn is more expensive per night because 475 is greater than 350.
e the problem.
1) Scores on a test are approximately normally distributed with a mean of 70 and a standard deviation of 9. The
teacher wants to give A's to the top 10% of students, B's to the next 25%, and C's to the next 42%. What is the
bottom cutoff for a C grade? Round your answer to the nearest whole number..
A) 68
B) 63
C) 77
D) 65
Answers
z = -1.34 < (a - 70)/9
And if we solve for we got
a = 70 - 1.34 * 9 = 57.95 = 98
So, the value of height that separates the bottom 9% of data from the top 91% is 58.
And the answer for this case would be:
a) 58
What is the Normal distribution and Z-score?
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
The solution to the problem
Let X be the random variable that represents the scores of a population, and for this case we know the distribution for X is given by:
X ~ N (70, 9)
Where μ = 70, and σ = 9
For this case, the figure attached illustrates the situation for this case.
We know from the figure that the lower limit for D accumulates 9% or 0.09 of the area below and 0.91 or 91% of the area above.
we want to find a value a, such that we satisfy this condition:
P(X > a) = 0.91 (a)
P(X < a) = 0.09 (b)
Both conditions are equivalent in this case. We can use the z score again in order to find the value a.
As we can see in the figure attached the z value that satisfies the condition with 0.09 of the area on the left and 0.91 of the area on the right it's z=-1.34. On this case P(Z<-1.34)=0.09 and P(z>-1.34)=0.91
If we use condition (b) from the previous we have this:
P(X < a) = P(X - μ)/σ < (a - μ)/σ) = 0.09
P(z < (a - μ)/σ) = 0.09
But we know which value of z satisfies the previous equation so then we can do this:
z = -1.34 < (a - 70)/9
And if we solve for we got
a = 70 - 1.34 * 9 = 57.95 = 98
Hence, the value of height that separates the bottom 9% of data from the top 91% is 58.
And the answer for this case would be:
a) 58
To learn more about the Normal distribution and Z-score visit,
https://brainly.com/question/14812280
#SPJ1
Find the length of the third side. If necessary, round to the nearest tenth

Answers
Answer:
30
Step-by-step explanation:
third side is the hypotenuse since it is opposite to 90 degree.
using pythagoras theorem
a^2 + b^2 = c^2
24^2 + 18^2 = c^2
576 + 324 = c^2
900 = c^2
\(\sqrt{900}\) = c
30 = c
therefore third side is 30.
Answer:
30
Step-by-step explanation:
\( {24}^{2} + 18 {}^{2} = c {}^{2} \\ 576 + 324 = c {}^{2} \\ \sqrt{900 = \sqrt{c }^{2} } \\ = 30\)
PLEASE HELP PLEASE AND THANK YOU HAVE A BLESSED DAY

Answers
the fractions with the same denominator will be 14/16 and 13/16.
What is a fraction?
If the numerator is bigger, it is referred to as an improper fraction and can also be expressed as a mixed number, which is a whole-number quotient with a proper-fraction remainder.
Any fraction can be expressed in decimal form by dividing it by its denominator. One or more digits may continue to repeat indefinitely or the result may come to a stop at some point.
The given fraction is given are 7/8 and 13/16.
Taking lcm of the denominator will be 16
So the fraction will be 7*2 = 14
So the fractions will be 14/16 and 13/16.
Hence the fractions with the same denominator will be 14/16 and 13/16.
Learn more about Fractions, by the following link.
https://brainly.com/question/17220365
#SPJ1
Solve the inequality, and write the solution set in interval notation if possible. Write numbers as simplified fractions or integers.6w-71 +751The solution set is
Answers
we have the inequality
|6W-7|+7 ≤ 1
step 1
Solve the first case (positive case)
+(6w-7)+7 ≤ 1
6w ≤ 1
w ≤ 1/6
The solution to the first inequality is (-infinite, 1/6]
step 2
Solve the second case (negative case)
-(6w-7)+7 ≤ 1
Multiply by -1 on both sides of the inequality
(6w-7)-7 ≥ -1
6w-14 ≥ -1
6w ≥ -1+14
6w ≥ 13
w ≥ 13/6
The solution to the second inequality is [13/6, infinite)
therefore
The solution toof the given inequality is
(-infinite, 1/6] ∩ [13/6, infinite)=Ф
there is no solution
A high-altitude spherical weather balloon expands as it rises due to the drop in atmospheric pressure. Suppose that the radius r increases at the rate of 0.03 inches per second and that r=48 inches at time t=0. Determine a function that models the volume V of the balloon at time t and find the volume at t=300 seconds.
Answers
Considering a linear function for the radius, we have that:
The volume of the sphere is modeled by \(V(t) = \frac{4\pi(0.03t + 48)^3}{3}\).After 300 seconds, it is of 775,735 in³.What is a linear function?A linear function is modeled by:
\(y = mx + b\)
In which:
m is the slope, which is the rate of change, that is, by how much y changes when x changes by 1.b is the y-intercept, which is the value of y when x = 0, and can also be interpreted as the initial value.What is the volume of a sphere?The volume of a sphere of radius r is given by:
\(V = \frac{4\pi r^3}{3}\)
In this problem, radius r increases at the rate of 0.03 inches per second and that r=48, hence it is represented by the following linear function:
\(r(t) = 0.03t + 48\)
Thus, the volume of the sphere is given by:
\(V = \frac{4\pi r(t)^3}{3}\)
\(V(t) = \frac{4\pi(0.03t + 48)^3}{3}\)
After 300 seconds, the volume in cubic inches is given by:
\(V(300) = \frac{4\pi(0.03(300) + 48)^3}{3} = 775735\)
More can be learned about linear functions at https://brainly.com/question/24808124
Please and thank you this is a must so plz answer!


Answers
Answer:
The one on the top right
Step-by-step explanation:
For 1 ticket its $10. That graph shows each number of tickets by 10.
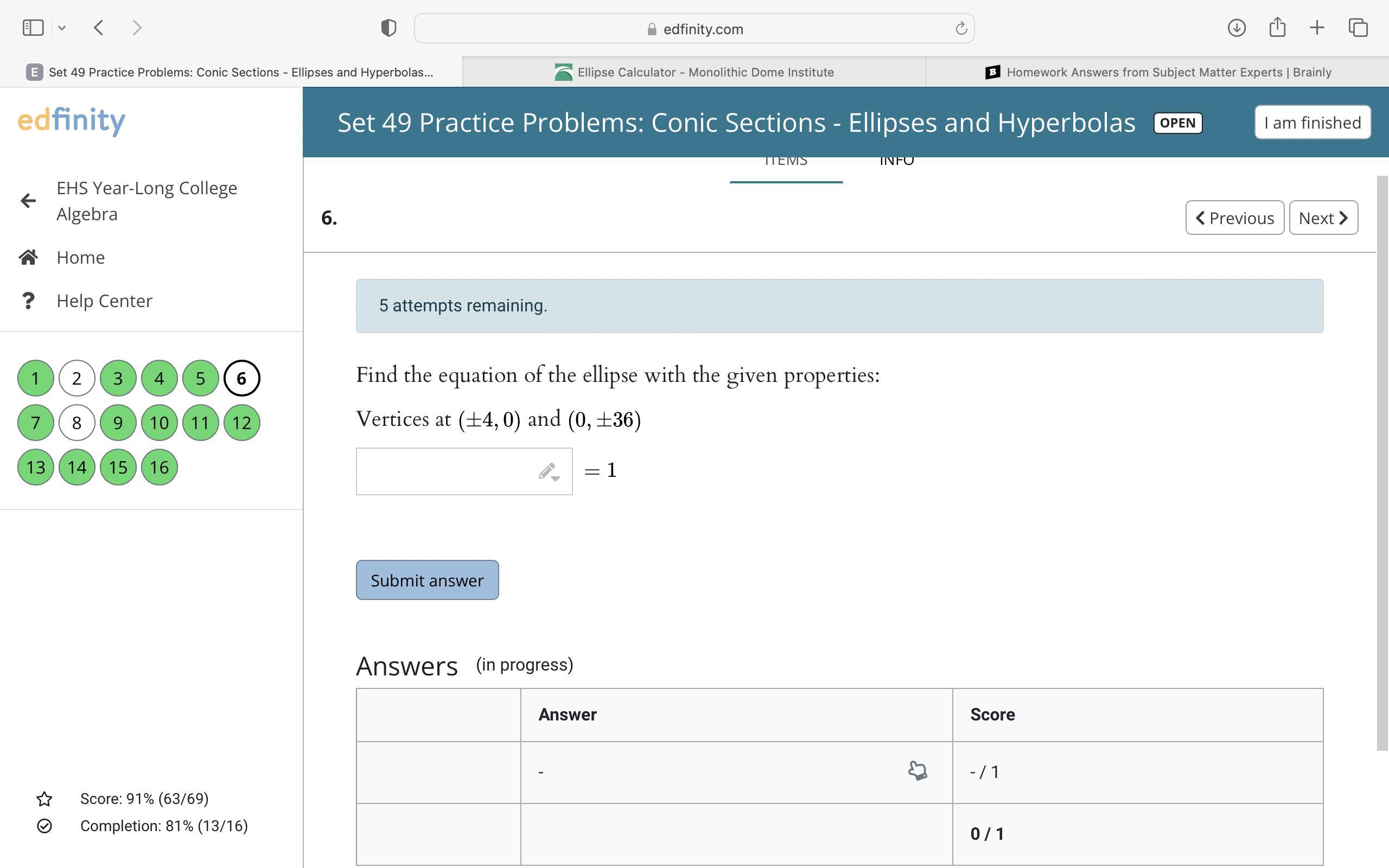
I need helping finding the equation of the ellipse please.
Answers
Turn me into a superhero
HELP PLEASEEEEEEE!!!!!

Answers
The similar shapes EFGH and JKLM have the measurement of angle Z equal to 65°, the length x = 27.5 and the length of y = 12
What are similar shapesSimilar shapes are two or more shapes that have the same shape, but different sizes. In other words, they have the same angles, but their sides are proportional to each other. When two shapes are similar, one can be obtained from the other by uniformly scaling (enlarging or reducing) the shape.
Given that the shape EFGH is a smaller shape of JKLM, and they are similar, then:
the measure of angle Z is equal to 65°
the side EF corresponds to JK and side FG corresponds to KL, so:
8/20 = 11/x
x = (11 × 20)/8 {cross multiplication}
x = 27.5
the side EF corresponds to JK and EH corresponds to JM, so:
8/20 = y/30
y = (30 × 8)/20 {cross multiplication}
y = 12
Therefore, the similar shapes EFGH and JKLM have the measurement of angle Z equal to 65°, the length x = 27.5 and the length of y = 12
Read more about similar shapes here: https://brainly.com/question/21823811
#SPJ1
The function is defined below. Find all values of that are NOT in the domain of g. g(x)=x^2+13+40 / x^2-9
Answers
Answer:
g(x)=x-2/x^2-9
If there is more than one value, separate them with commas.
Step-by-step explanation: