Given t₃=3⁵+3⁴+6+2,find the value of t.
Answers
Answer: t=332
Step-by-step explanation: Simplify 3^5+3^4+6+2.
Related Questions
Simplify 9 + (-2)^3
helpppp
Answers
Answer:
1
Step-by-step explanation:
9 + (-2)^3
We know that (-2)^3 means (-2)*(-2)*(-2) = -8
9+-8 = 1
A random sample of size 36 is taken from a normal population with a mean of 50 and a standard deviation of 5. What is the sample standard deviation?
Answers
The sample standard deviation is approximately 0.83.
Sample size \(($n$)\) = 36
Population mean \(($\mu$)\) = 50
Population standard deviation \(($\sigma$)\) = 5
The sample standard deviation, denoted as \($s$\) can be estimated using the formula:
\(\[ s = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}} \]\)
where:
\($x_i$\) represents the individual data points in the sample
\($\bar{x}$\) is the sample mean
In this case, since we don't have individual data points, we can use the population standard deviation as an estimate for the sample standard deviation when the sample size is relatively large (as in this case \($n = 36$\)). This approximation is known as the standard error of the mean.
Therefore, the sample standard deviation can be approximated as:
\(\[ s \approx \frac{\sigma}{\sqrt{n}} \]\)
Substituting the given values:
\(\[ s \approx \frac{5}{\sqrt{36}} = \frac{5}{6} \] = 0.83\)
Hence, the sample standard deviation is approximately 0.83.
Learn more about sample standard deviation: https://brainly.com/question/18567452
#SPJ11
Consider the following public good provision game. Players can choose either to contribute (C) or not contribute (NC) to the public good. If someone contributes, both will be able to consume the good, which worths v dollars and is publicly known. The player i's cost to contribute is Cᵢ, which is private information. It is common knowledge that C₁,C₂ are drawn from a uniform distribution with support (Cₗ, Cₕ]. Assume v > Cₕ. C NC
C ᴠ - C₁ . ᴠ - C₂ ᴠ - C₁, ᴠ
(a) Suppose player 2 contributes if C₂ < C*₂, where C*₂ is a cutoff point. What is the expected payoff for player 1 to contribute and not contribute? What would player 1 do when C₁ is low? (b) Suppose player 1 also employ a cutoff strategy. Solve for the cutoff point (C*₁, C*₂). What is the Bayesian Nash equilibrium of the game?
Answers
In the given public good provision game, player 1's expected payoff for contributing and not contributing depends on player 2's cutoff point (C*₂). When player 1 contributes, their payoff is v - C₁ if C₁ < C*₂, and 0 if C₁ ≥ C*₂. When player 1 does not contribute, their payoff is always 0.
How does player 1's expected payoff vary based on player 2's cutoff point (C*₂)?In this public good provision game, player 1's decision to contribute or not contribute depends on their private cost, C₁, and player 2's cutoff point, C*₂. If player 1 contributes, they incur a cost of C₁ but gain access to the public good valued at v dollars. However, if C₁ is greater than or equal to C*₂, player 1's expected payoff for contributing would be 0 since player 2 would not contribute.
On the other hand, if player 1 does not contribute, their expected payoff is always 0, as they neither incur any cost nor receive any benefit from the public good. Therefore, player 1's expected payoff for not contributing is constant, irrespective of the cutoff point.
To determine player 1's expected payoff for contributing, we consider the case when C₁ is less than C*₂. In this scenario, player 2 contributes to the public good, allowing both players to consume it. Player 1's payoff would then be v - C₁, which represents the value of the public good minus their cost of contribution. However, if C₁ is greater than or equal to C*₂, player 1's contribution would be futile, as player 2 would not contribute. In this case, player 1's expected payoff for contributing would be 0, as they would not gain access to the public good.
In summary, player 1's expected payoff for contributing is v - C₁ if C₁ < C*₂, and 0 if C₁ ≥ C*₂. On the other hand, player 1's expected payoff for not contributing is always 0. Therefore, when C₁ is low, player 1 would prefer to contribute, as long as the cost of contribution is less than player 2's cutoff point.
Learn more about public good provision game
brainly.com/question/32069754
#SPJ11
Six friends have these three graham crackers, which were each split into a different number of pieces.
How can the six friends share the graham crackers equally, without breaking any of the pieces?
Answers
Answer:
Two rectangles
Step-by-step explanation:
the normal gram cracker can be broken into 4 rectangles so that's what was probably done when THEY split it ( says it in the question) so they can all get two rectangles!
Happy Saint Patricks day!
( Can I get brainlyist?)
suppose you always reject the null hypothesis, regardless of any sample evidence. (a) what is the probability of type ii error?
Answers
In hypothesis testing, the probability of a Type II error (β) is the probability of failing to reject the null hypothesis when it is actually false. Since you always reject the null hypothesis, the probability of committing a Type II error is zero (β = 0).
The probability of a Type II error depends on the specific alternative hypothesis, the sample size, the significance level, and the power of the test. However, in the scenario you described, where the null hypothesis is always rejected, the Type II error probability is inherently zero. This is because a Type II error occurs when we fail to reject the null hypothesis even though it is false, but in this case, we never fail to reject it.
By always rejecting the null hypothesis, you are essentially adopting a stance that any sample evidence is sufficient to reject it. This approach can be considered overly aggressive and disregards the potential for false negatives. Type II errors can occur when the sample evidence is not strong enough to provide convincing support against the null hypothesis, leading to a failure to reject it. However, in this scenario, that possibility is entirely disregarded, resulting in a Type II error probability of zero.
To learn more about probability click here brainly.com/question/32117953
#SPJ11
Given the equation y= 2x - 8, what is the slope and the y-intercept?
Om = 2 and b= 8
O m= 2 and b= -8
m= 8 and b=2
O m= -8 and b= 2
Answers
mx+b !!
|x–5|=–5 plzz help me
Answers
Answer:
(0-5)=-5
-5-5 = 0
x=0
Step-by-step explanation:
D=(x2+x1)+(y2-y1) this is the formula I need number 19 Please will mark brainliest and 50 points

Answers
Answer:
\(2\sqrt{2}\) or \(\sqrt{8}\\\)
Step-by-step explanation:
The formula is actually d= \(\sqrt{(x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}}\). Now first, we have to find points A and C.
Point A is (1,2) and Point C is (-1,0).
Now we have to substitute the values in. That would make it d =\(\sqrt{(-1-1)^{2} + (0-2)^{2}}\).
To simplify the parentheses, it would get to d= \(\sqrt{(-2)^{2}+(-2)^{2} }\).
To simplify the exponents, it would get to d = \(\sqrt{4+4}\).
To simplify the square root, it would get to d = \(\sqrt{8}\).
So the answer is either \(2\sqrt{2}\) or \(\sqrt{8}\\\).
Hope this helped! If not, please let me know!
PLZZZ HELP ME!! Solve for x Simplify your answer as much as possible

Answers
Answer:
x=14
Step-by-step explanation:
1.) Add 11 to both sides
2.) divide both sides by 3
Step 1: you move the constant to the right
3x=31+11
Step 2: calculate the left side first
3x=42
Step 3: then divide both sides by 3
x=14
Step 4: and then you have your answer
help please and thank you!
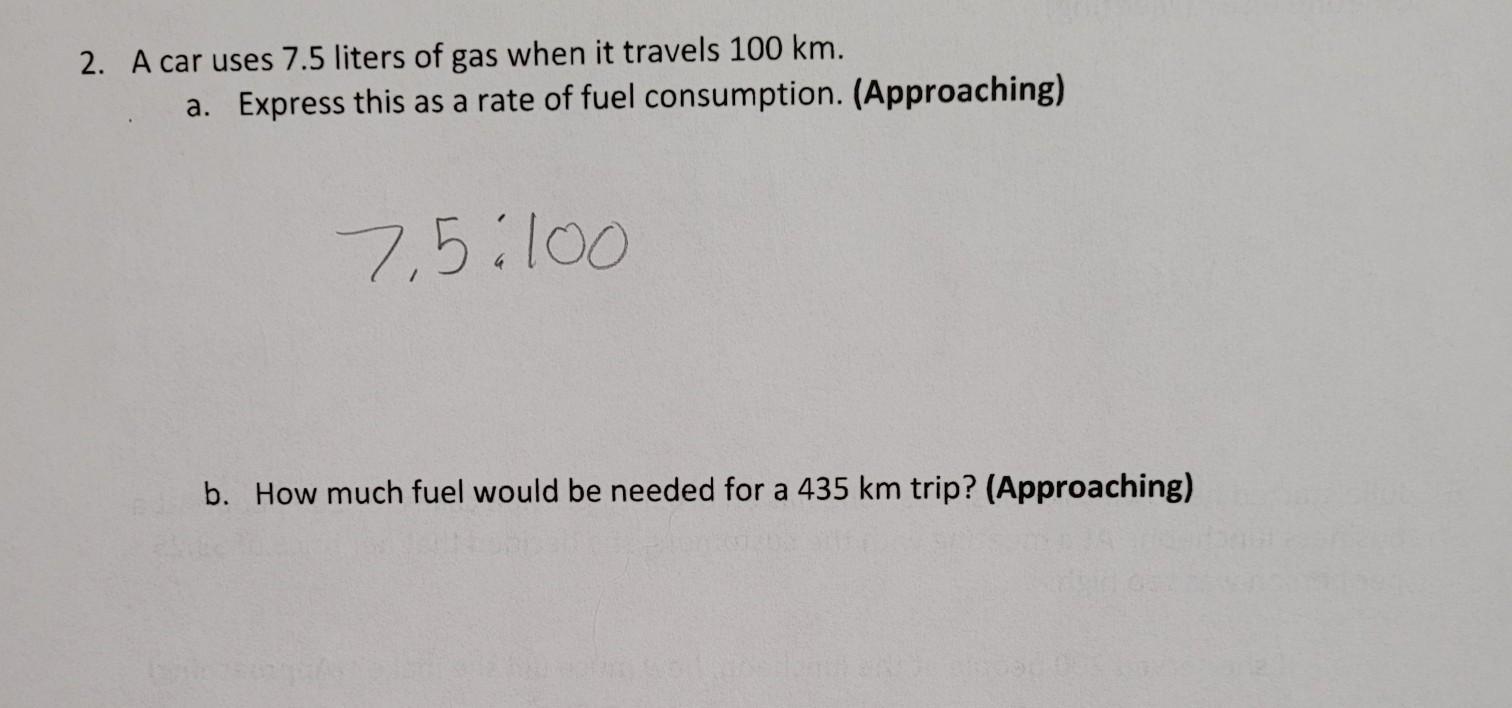
Answers
Answer: First one correct
Step-by-step explanation:
The second one is
7.5 x 4 = 30 liters for 400km
and the 35 = 35%
and 35% of 7.5 is 2.625
so 30 + 2.625 = 32.625
Suppose that R is the finite region bounded by f(x) = 4√x and g(x) = x/3. Find the exact value of the volume of the object we obtain when rotating R about the x-axis. V = 27π/10 x
Find the exact value of the volume of the object we obtain when rotating R about the y-axis. V= 9π/2 x
Answers
We are given two functions, f(x) = 4√x and g(x) = x/3, which define a finite region R. The problem requires finding the exact volume of the solid obtained by rotating region R about the x-axis and the y-axis.
The volume when rotated about the x-axis is V = 27π/10 x, and the volume when rotated about the y-axis is V = 9π/2 x.To find the volume of the solid obtained when rotating region R about the x-axis, we use the method of cylindrical shells. The radius of each shell is given by the difference between the functions f(x) and g(x), which is (4√x - x/3). The height of each shell is dx. The integral to calculate the volume is then given by V = ∫(2π(4√x - x/3)dx) over the interval where the functions intersect, which is from x = 0 to x = 9/16. Evaluating this integral gives V = 27π/10 x.
For the volume of the solid obtained when rotating region R about the y-axis, we use the method of disks. The radius of each disk is given by the functions f(x) and g(x). The height of each disk is dy. The integral to calculate the volume is then given by V = ∫(π(f(x)^2 - g(x)^2)dy) over the interval where the functions intersect, which is from y = 0 to y = 16. Simplifying and evaluating this integral gives V = 9π/2 x.
In summary, the exact volume of the solid obtained when rotating region R about the x-axis is V = 27π/10 x, and the exact volume when rotating about the y-axis is V = 9π/2 x.
To learn more about volume of the solid click here : brainly.com/question/26522966
#SPJ11
Can someone please help me on this and explain if you can!

Answers
Answer:
x = \(11\sqrt{2}\)
y = \(11\sqrt{2}\)
Step-by-step explanation:
the ratio of the sides of a 45 - 45 - 90 triangle is shown at the bottom of this answer.
as you can see, it is x:x:\(x\sqrt{2}\)
The side given is x\(\sqrt{2}\), so you have:
\(x\sqrt{2}=22\)
divide both sides by \(\sqrt{2}\)
x = \(22/\sqrt{2}\)
multiply this by \(\sqrt{2} /\sqrt{2}\)
\(x = 22\sqrt{2}/2\)
\(x=11\sqrt{2}\)
y is also equal so y = \(11\sqrt{2}\)

Lewis wants to play several games of paintball with his friends. At the park, it costs $19.31 for admission and paintballs, and $6.71 for each game he plays. Which of the following equations could be used to determine Lewis's total cost for several games of paintball?(Let x represent the number of games Lewis plays and y represent his total cost.)
A.
y = $6.71x
B.
$19.31y = $6.71x
C.
y = $19.31x + $6.71
D.
y = $6.71x + $19.31
Answers
A particular fruit's weights are normally distributed, with a mean of 459 grams and a standard deviation of 25 grams. If you pick one fruit at random, what is the probability that it will weigh between 470 grams and 539 grams A manufacturer knows that their items have a normally distributed lifespan, with a mean of 2.9 years, and standard deviation of 0.9 years. The 9% of items with the shortest lifespan will last less than how many years? Give your answer to one decimal place
Answers
The probability that a randomly picked fruit will weigh between 470 grams and 539 grams is approximately 33.07%. The lifespan below which 9% of items fall is approximately 1.7 years.
To calculate the probability that a randomly picked fruit will weigh between 470 grams and 539 grams, we need to standardize the values and use the standard normal distribution.
First, we calculate the z-scores for the given weights using the formula:
z = (x - μ) / σ
where x is the weight, μ is the mean, and σ is the standard deviation.
For the lower value of 470 grams:
z1 = (470 - 459) / 25 ≈ 0.44
For the upper value of 539 grams:
z2 = (539 - 459) / 25 ≈ 3.20
Next, we use a standard normal distribution table or a calculator to find the probabilities associated with these z-scores.
The probability of a fruit weighing less than 470 grams (z < 0.44) is the cumulative probability up to z1.
The probability of a fruit weighing less than 539 grams (z < 3.20) is the cumulative probability up to z2.
To find the probability between 470 grams and 539 grams, we subtract the cumulative probability of z1 from the cumulative probability of z2.
P(470 < x < 539) = P(z1 < z < z2)
Now, let's calculate these probabilities:
P(z < 0.44) ≈ 0.6686 (from standard normal distribution table or calculator)
P(z < 3.20) ≈ 0.9993
P(470 < x < 539) ≈ P(z1 < z < z2) ≈ 0.9993 - 0.6686 ≈ 0.3307
Therefore, the probability that a randomly picked fruit will weigh between 470 grams and 539 grams is approximately 0.3307, or 33.07%.
For the second part of the question, to determine the lifespan below which 9% of items fall, we need to find the corresponding z-score.
From the standard normal distribution table or calculator, we find the z-score associated with a cumulative probability of 9%, which is approximately -1.34.
Using the z-score formula and solving for x:
z = (x - μ) / σ
-1.34 = (x - 2.9) / 0.9
Solving for x:
x - 2.9 = -1.34 * 0.9
x - 2.9 ≈ -1.206
x ≈ 2.9 - 1.206 ≈ 1.694
Therefore, the 9% of items with the shortest lifespan will last less than approximately 1.7 years.
Note: It's important to keep in mind that these calculations assume a normal distribution and may vary slightly depending on the specific approximation method used or the degree of precision required.
To know more about standard normal distribution, refer to the link below:
https://brainly.com/question/26822684#
#SPJ11
A coach of a baseball team orders hats for the players on his team. Each hat costs .The shipping charge for the entire order is . There is no tax on the order. The total cost of the coach’s order is less than . Which inequality can be used to determine the greatest number of hats, , the coach orders?
Answers
Answer:
9.95h + 5 < 125
Step-by-step explanation:
You left out the numbers to solve the question, but I've already encountered this question before, so yeah.
Determine whether the coordinate plane shows a reflection in the x -axis, y -axis, or neither.
IC С
B
D
-4
A
4x
E
-2
F
-4
1
Answers
Answer:
Step-by-step explanation:
Neither
The times taken by Amal to run three races were 3 minutes 10 seconds, 2 minutes 58.2 seconds and 3 minutes 9.8 seconds. Find the average time taken, giving your answer in minutes.
Answers
Approximately it is:
3 minutes 19 seconds
Q6 (6 marks) A utility company will not use coal with a sulfur content of more than 2.25. What percent of coal is in this category given that the target sulfur value is 1.65 and the standard deviation is 0.617. If the target is changed to 1.45, how this will affect the percent of coal accepted by the utility company (fully show your calculations). Q7 (6 marks) A juice bottle has an upper specification of 1.03 liters and a standard deviation of 0.02 liters. The data is normally distributed. Show detailed answer to the following questions. a. If 1.5% of the data is to be above the upper specification, where should the process center be located? Round to the nearest three significant digits. b. If the production for that month is 43,000 juice bottles, how many juice bottles will be 0.99 liters or less?
Answers
The percent of coal with sulfur content exceeding 2.25 is approximately 21.35%. If the target sulfur value is changed to 1.45, the effect on the percent of coal accepted by the utility company will be explained in Step 2.
To determine the percent of coal with sulfur content exceeding 2.25, we need to calculate the z-score for the target sulfur value of 1.65 using the formula:
z = (x - μ) / σ
where x is the target sulfur value, μ is the mean sulfur value, and σ is the standard deviation.
Given that the target sulfur value is 1.65, the standard deviation is 0.617, and assuming the mean sulfur value is 2.25 (as the utility company will not use coal with sulfur content above this value), we can calculate the z-score:
z = (1.65 - 2.25) / 0.617
≈ -0.972
Using a standard normal distribution table or calculator, we can find the area to the left of this z-score, which represents the percentage of coal with sulfur content below 2.25. In this case, the area to the left of -0.972 is approximately 0.1667.
To find the percent of coal in the category with sulfur content exceeding 2.25, we subtract the above value from 1 (since the total percentage must add up to 100):
Percent = 1 - 0.1667
≈ 0.8333 or 83.33%
Now, if the target sulfur value is changed to 1.45, we repeat the same calculations. Using the new target value, the z-score can be calculated as:
z = (1.45 - 2.25) / 0.617
≈ -1.297
Again, finding the area to the left of -1.297 in the standard normal distribution, we obtain approximately 0.0968. Subtracting this value from 1 gives us the new percent of coal in the category with sulfur content exceeding 2.25:
New Percent = 1 - 0.0968
≈ 0.9032 or 90.32%
Therefore, changing the target sulfur value to 1.45 increases the percent of coal accepted by the utility company to approximately 90.32%.
Learn more about percent of coal
brainly.com/question/32412636
#SPJ11
Solve for the ? angle

Answers
Answer:
50
Step-by-step explanation:
since all angles add up to 180
and since this is a right triangle the square in the corner is 90 degrees
so 40+90+x=180
130+x=180
subtract 130 from both sides
130-130+x=180-130
x=50
Hope that helps :)
Helppppp pleaseeeee

Answers
Answer:
3.75
Step-by-step explanation:
5 tables every 2 months,then 30 days (30 days in 1 month) / 8 ordes = 3.75
Al has a cylindrical storage container 30 centimeters tall with a diameter of 22 centimeters. How much bird food in cubic centimeters will fit in the container? Use the formula V = Bh and approximate π using 3.14. Round your answer to the nearest tenth.
Answers
The amount of bird food in cubic centimeters will fit in the container is
11, 398. 2 cubic centimeters
How to determine the volumeThe formula that is used for calculating the volume of a cylinder is expressed with the equation;
V = π(d/2)²h
Such that the parameters of the given equation are;
V is the volume of the cylinder.d is the diameter of the cylinderh is the height of the cylinderNow, substitute the values into the formula, we have;
Volume = 3.14 (22/2)² 30
divide the values
Volume = 3.14(121)30
Now, multiply the values and expand the bracket
Volume = 11, 398. 2 cubic centimeters
Learn about cylinders at: https://brainly.com/question/9554871
#SPJ1
Write the compound inequality: " A number n is less than or equal to -7 or greater than 12
Answers
Let the number be n, then -1<3n+5<38 or -1≤3n+5≤38 depending on what is meant by “between”. We’ll assume the former.
-1<3n+5<38, subtract 5 throughout: -6<3n<33, divide through by 3: -2<n<11, shows the number to be in the range (-2,11) or possibly [-2,11].
PLEASE HELP! 100 POINTS
The sequence defined recursively by x, = V1996x -1 and Xo = 1 approaches a limiting value as
n grows infinitely large.
Would this be true if a different value were assigned to xo?
Answers
The limiting value of the sequence will be the same even if a different value is assigned to x0.
The limiting value of the sequence is determined by the recursive equation xn = √(1996x\(n^{-1}\)). As n grows infinitely large, the value of xn will approach the same limiting value regardless of the initial value assigned to x0. This is because the recursive equation will continue to generate values that are closer and closer to the limiting value, regardless of the starting point.
Therefore in recursive equations, the limiting value of the sequence will be the same even if a different value is assigned to x0.
More on recursive equations can be researched here: https://brainly.com/question/8972906
#SPJ11
What is the approximate length of the radius, r? a. 4.5 cm b. 9.0 cm c. 14.2 cm d. 28.3 cm
Answers
The approximate length of the radius, r is 4.51 cm. SO the option 1 is correct.
In the given question we have to find the approximate length of the radius, r.
As given, circle O has a circumference of approximately 28.3 cm.
The calculation of the circle's boundary is referred as the perimeter or circumference of the circle. Although the circumference of the circle determines the space it occupies.
The circumference of a circle is its length when it's actually opened and represented as a single direction. Units like cm or unit m are typically used to measure it.
As we know that the formula of circumference of circle = 2πr
As circumference of circle = 28.3 cm
So 2πr = 28.3 cm
Divide by 2π on both side, we get
r = 14.15/π
π = 3.14
So r = 14.15/3.14
r = 4.51 cm
To learn more about circumference of circle link is here
brainly.com/question/11213974
#SPJ4
The complete question is:
Circle O has a circumference of approximately 28.3 cm.
What is the approximate length of the radius, r?
a. 4.5 cm
b. 9.0 cm
c. 14.2 cm
d. 28.3 cm
The approximate length of the radius, r, is 4.5 cm.
The formula for calculating the radius, r, of a circle is r = C/2π, where C is the circumference of the circle. In order to calculate the approximate length of the radius, we must first calculate the circumference.
Let's assume that the circumference of the circle is 28.3 cm. To calculate the circumference, we can use the formula C = 2πr. We know the circumference and want to solve for the radius, so we can rearrange the formula to solve for r: r = C/2π.
Plugging in our values, we can calculate the approximate length of the radius: r = 28.3 cm/2π = 4.5 cm. Therefore, the approximate length of the radius, r, is 4.5 cm.
Learn more about length of the radius here:
https://brainly.com/question/16142828
#SPJ4
A chemist has 13 1/3 fluid ounces of a solution. How many containers can he fill if each container holds 5/12 ounces?
Answers
The weight of the solution is 13 1/3 ounces.
Each container can contain 5/12 ounces.
The number of container required can be determined as,
\(\begin{gathered} N=\frac{13\frac{1}{3}}{\frac{5}{12}} \\ =\frac{\frac{40}{3}}{\frac{5}{12}} \\ =\frac{40}{3}\times\frac{12}{5} \\ =32 \end{gathered}\)Thus, the requried number of containers is 32.
Step by step
13 1/3 total divided by 5/12 containers
40/3 divided by 5/12
When you divide fractions you flip the divisor and multiply
40/3 x 12/5 = 32 containers of 5/12 ounces
Use the remainder theorem for x^3+8x^2+11x-20 by x+4. Use the remainder theorem for x^3+8x^2+11x-20 by x-5.
Answers
Answer:
the remainder for both expressions is zero
Step-by-step explanation:
(x+4)=0x=-4x³+8x²+11x-20, where x=-4(-4)³+8(-4)²+11(-4)-20-64+128-44-200, Hence it has no remainder (x+5)=0x=-5x³+8x²+11x-20, where x=-5(-5)³+8(-5)²+11(-5)-20-125+200-55-200, hence it has no remainder5 4 2 2 2 2 1 1 3 2 2 3 3 2 1
can someone find the median mode and please show how you got it :)
you will get top answer
Answers
Answer:
mode = 2
Step-by-step explanation:
mode is the most frequently seen number.
median is the average so 5+4+2+2+2+2+1+1+3+2+2+3+3+2+1/15= 2 1/3
Answer:
Median is 2, Mode is 2
Step-by-step explanation:
1,1,1,2,2,2,2,2,2,2,3,3,3,4,5 to get the median you put the number from smallest to large then you x one out on each side until there is only one number left which would be 2
The mode is 2 because it is the most common number (aka it appears the most in the list)
can i have help please?

Answers
Answer:
38
Step-by-step explanation:
(34+ 18 × q)-(5^q + 7). q=2
34+18×2-(5²+7)
34+18×2-(25+7)
34+18×2-32
34+36-32
38
semoga membantu
Answer:
38
brainliest is appreciated
Step-by-step explanation:
q=2
(34 + 18 . q) - (5^q + 7)
(34 + 18 × 2) - (5^2 + 7)
70 - 32
38
what part of the equation g(x)=1-x^2 says that it will be open downward
Answers
Answer:
coefficient of x²
Step-by-step explanation:
Co-efficient of x² says if the parabola is open upward or downward.
If the coefficient of x² is positive, the parabola is open upward.
If the coefficient of x² is negative, the parabola is open downward.
A restaurant owner wants to determine the effectiveness of his servers. the owner places a survey regarding the servers' effectiveness with randomly selected customer bills. what is the sample? a. the sample is the randomly selected customers. b. the sample is all customers of the restaurant. c. the sample is the servers. d. the sample is the owner of the restaurant.
Answers
The sample is the randomly selected customers (Option B).
What is sample?
Suppose we have to estimate the proportion of New York state residents who are Seattle Seahawks fans. Say, 500 New York state residents are randomly selected, whether they are Seattle Seahawks fans or not, and expand this to the entire population of New York State residents.In this case:The sample is 500 residents.The population is all New York State Residents.Now, according to the question, a survey is passed to the customers.
Here, the sample is the customers.
Hence, the sample is customers and the correct choice of options is (C).
To learn more about sample, refer to the link : https://brainly.com/question/12892403
#SPJ4
Answer:
randomly selected customers n
Step-by-step explanation:
plato 022