given the following quadratic equation, what is the value of A? 5x^2+8x-4
*5
*2
*8
*4
Answers
Answer:
a =5
Step-by-step explanation:
5x^2+8x-4
A quadratic can be written as
ax^2 +bx+c
a=5 b=8 c=-4
Answer:
The value of A is 5
Step-by-step explanation:
Because it is written in a quadratic equation
Related Questions
please help factorise 7ab+a
Answers
Answer:
= a(7b + 1)
Step-by-step explanation:
7ab + a
a(7b + 1).
Multiple Choice What is the sum of five-sixths + start fraction 2 over 3 end fraction? A. one and one-third B. One and one half C. 1 and two-thirds D. The fraction states 1 and 3 fourths.
Answers
Answer:
B
Step-by-step explanation:
\(\frac{5}{6} +\frac{2}{3} \\\\=\frac{5}{6}+\frac{2*2}{2*3} \\\\=\frac{5}{6}+\frac{4}{6} \\\\=\frac{5+4}{6} \\\\=\frac{9}{6} \\\\=\frac{3*3}{3*2} \\\\=\frac{3}{2}\)
\(=\frac{2+1}{2} \\\\=\frac{2}{2}+\frac{1}{2} \\\\=1+\frac{1}{2}\)
B.One and one half
PLEASE HELP!!!! 20 POINTSSSS!!!!!!!!!!
I WOULD MARK BRAINLIEST!!!!!!!!!!!!!!


Answers
Answer:
a=b sinα
sinβ=5·sin(22°)
sin(119°)≈2.14154
a=b sinα
sinβ=12·sin(48°)
sin(42°)≈13.32735
Step-by-step explanation:
I think this is correct but i am most likely wrong, Im not that great at math
Answer:
( SOLVE FOR h )
Step-by-step explanation:
THE FORMULA:
a = b \(\frac{sin A}{sin B}\)
---------
b = 12
sin a = 48
sin B = 42
--------
12 × \(\frac{sin 48}{sin 42}\)
ANSWER =
h = 13.33
----------------------------------------
SOLVE FOR x AND y
I'M NOT SURE.......
x = 2.14
b = 5
When you are determining the observed t-test or the confidence interval, what is the major difference between an independent samples design and the dependent samples design? Select one:
A. The numerators are different.
B. The independent variable is nominal scaled for an independent samples t-test and the independent variable is interval or ratio scaled for a dependent samples t-test.
C. The two standard errors are calculated differently.
D.The two means are calculated differently.
Answers
The major difference between an independent samples design and a dependent samples design when determining the observed t-test or the confidence interval is:
C. The two standard errors are calculated differently.
Determine the independent sample design?In an independent samples design, where two separate groups are being compared, the standard errors for the means of each group are calculated separately. The standard error measures the variability of the sample means around the population means. In this case, since the groups are independent, the standard errors are calculated independently.
On the other hand, in a dependent samples design, also known as a paired or matched design, the groups are related or paired in some way (e.g., before and after measurements on the same individuals).
In this design, the standard errors are calculated differently because the observations within each pair or group are dependent on each other. The standard errors consider the covariance or correlation between the paired observations, reflecting the within-pair variability.
Therefore, (C) the calculation of standard errors differs between independent samples and dependent samples designs when determining the observed t-test or the confidence interval.
To know more about independent sample, refer here:
https://brainly.com/question/29342664#
#SPJ4
Jim provides photos for two online sites: site A and site B. Site A pays $0.85 for every photo Jim provides. The amount in dollars (y) site B pays as a function of the number of photos provided (x) is represented by the equation y = 0.40x. How much more was Jim paid at site A than at site B, if he provided five photos for each site? $1.15 $1.35 $2.15 $2.25
Answers
Answer:
Hello! I think the answer is D: $2.25. Please correct me if i'm wrong.
Step-by-step explanation:
Answer:
D: $2.25
Step-by-step explanation:
Evaluate log0.25 2.
Picture below:

Answers
Answer:
A
Step-by-step explanation:
using the property of logarithms
\(log_{b}\) x = n ⇒ x = \(b^{n}\)
let \(log_{0.25}\) 2 = n ( solve for n ) , then
2 = \((0.25)^{n}\) = \((\frac{1}{4}) ^{n}\) = \((\frac{1}{2^2}) ^{n}\) = \((2^{-2}) ^{n}\) = \(2^{-2n}\)
so
\(2^{-2n}\) = \(2^{1}\)
since bases on both sides are the same then equate exponents
- 2n = 1 ( divide both sides by - 2 )
n = \(\frac{1}{-2}\) = - \(\frac{1}{2}\)
Write a recursive formula for the arithmetic sequence:
7,4,1,-2
Answers
a(sub)n = a(sub)n-1 - 3
(sub) indicates the values touching the parenthesis are written as a subscript.
The above would be the recursive formula as you are taking the previous number and subtracting 3 to get the next number in the sequence.
Answer:
N - 3
Step-by-step explanation:
It is a series of -3 so:
7 -3 = 4
4 - 3 = 1
1 - 3 = -2
So:
N-3
where N is the present value in the sequence.
There are 7 books on the floor. The number of books on the shelf is 2 more than 3 times the number of books on the floor.
How many books are on the shelf?
please help
Answers
Answer:
the answer is 23
A research analyst disputes a trade group's prediction that back-to-school spending will average $606.40 per family this year. She believes that average back-to-school spending will significantly differ from this amount. She decides to conduct a test on the basis of a random sample of 20 households with school-age children. She calculates the sample mean as $628.85. She also believes that back-to-school spending is normally distributed with a population standard deviation of $45. Use 5% significance.
Part 1
State the null hypothesis and the alternative hypothesis for testing that the average back-to-school spending differs from $606.40.
Part 2
State the critical value(s) for testing this hypothesis.
Part 3
Calculate the test statistic Z for testing this hypothesis
Part 4
State and support your conclusions
Answers
Based on the calculations we have rejected the null hypothesis .
Given,
Standard deviation = $ 45
Random sample = 20
Now,
Part 1
Set the null hypothesis and alternative hypothesis,
\(H_{0} : u = 0\\ H_{0} : u > 606.40\)
Part 2
The value of z critical signifies 5% level of significance .
\(Z_{0.05} = 1.65\)
According to critical value if z after calculation is greater than or equal to 1.65 we reject the null hypothesis .
Part 3
The value of Z can be calculated by the formula,
Z = X - µ/σ/√n
Substitute the values ,
Z = 628.85 - 606.40/45/√20
Z = 1.93
Part 4
From the above calculation the value of Z is greater than the critical value .
Thus we reject the null hypothesis .
Know more about normal distribution,
https://brainly.com/question/15103234
#SPJ4
"√2n-5 = 10."
Please Show Step By Step
Answers
Answer is 15√2/2. I think.
Can I please help me ?!

Answers
Answer:
14 ft
Step-by-step explanation:
area = length * width
140 sq ft = 10 ft * width
width = (140 sq ft)/(10 ft)
width = 14 ft
What is the constant rate of this? Please show your work.

Answers
Answer:
3
Step-by-step explanation:
To find the answer, heres what you need to do.
Basically, you divide each number on the right by the number on the left.
15/5= 3
24/8=3
36/12=3
72/24=3
Since all of the answers are 3, your answer is 3
Answer:
3
Step-by-step explanation:
Slope Formula:
y2 - y1/x2 - x1
Let's use (5, 15) and (8,24)
(x1, y1) = (5, 15)
(y1, y2) = (8, 24)
Substitute:
y2 - y1/x2 - x1
24 - 15/8 - 5
Solve:
24 - 15/8 - 5
9/3
= 3
Therefore the slope, or constant rate is 3.
Tip: look at the relationship between Cost and Time.
15/5 = 3
24/8 = 3
36/12 = 3
72/24 = 3
Dividing is a simple way to find the slope!
PLEASE!!!!!!!!Evaluate: -5m 2t when m=6, t= -2
Answers
Answer:
120
Step-by-step explanation:
-5(6) 2(-2)
-5 x6 = -30. 2 x -2=-4
-30 x -4 = 120
the negatives cancel out :)
Help would be appreciated.

Answers
Answer:
Step-by-step explanation:
1). f(x) = x² - 9
g(x) = x - 3
h(x) = f(x) ÷ g(x)
= \(\frac{x^2-9}{x-3}\)
= \(\frac{(x+3)(x-3)}{(x-3)}\)
= (x + 3)
2). f(x) = x² - 4x + 3
= x² - 3x - x + 3
= x(x - 3) - 1(x - 3)
= (x - 1)( x- 3)
g(x) = x - 3
h(x) = f(x) ÷ g(x)
= \(\frac{(x-1)(x-3)}{(x-3)}\)
= (x - 1)
3). f(x) = x² + 4x - 5
= x² + 5x - x - 5
= x(x + 5) - 1(x + 5)
= (x - 1)(x + 5)
g(x) = x - 1
h(x) = f(x) ÷ g(x)
= \(\frac{(x-1)(x+5)}{(x-1)}\)
= (x + 5)
4). f(x) = x² - 16
= (x - 4)(x + 4) [Since a² - b² = (a - b)(a + b)]
g(x) = (x - 4)
h(x) = f(x) ÷ g(x)
= \(\frac{(x-4)(x+4)}{(x-4)}\)
= (x + 4)
Answer:
Step-by-step explanation:
1). f(x) = x² - 9
g(x) = x - 3
h(x) = f(x) ÷ g(x)
=
=
= (x + 3)
2). f(x) = x² - 4x + 3
= x² - 3x - x + 3
= x(x - 3) - 1(x - 3)
= (x - 1)( x- 3)
g(x) = x - 3
h(x) = f(x) ÷ g(x)
=
= (x - 1)
3). f(x) = x² + 4x - 5
= x² + 5x - x - 5
= x(x + 5) - 1(x + 5)
= (x - 1)(x + 5)
g(x) = x - 1
h(x) = f(x) ÷ g(x)
=
= (x + 5)
4). f(x) = x² - 16
= (x - 4)(x + 4) [Since a² - b² = (a - b)(a + b)]
g(x) = (x - 4)
h(x) = f(x) ÷ g(x)
=
= (x + 4)
What is the slope of a line parallel to the line whose equation is 2x-y=7. Fully simplify your answer.
Answers
Answer:
Step-by-step explanation:
Q
(
2
,
1
)
and
R
(
8
,
13
)
is partitioned from
Q
to
R
into a
1
:
2
ratio at point
Z
. What are the coordinates of
Z
?
Solve for the variable. Round to 3 decimal places
9
.Oh
x

Answers
\(\cos(40^o )=\cfrac{\stackrel{adjacent}{x}}{\underset{hypotenuse}{6}}\implies 6\cos(40^o )=x\implies 4.596\approx x\)
Make sure your calculator is in Degree mode.
solve 5^2x+1-5^2x=150 with steps
Answers
Answer:
x = 2.98
Step-by-step explanation:
5^2x + 1 - 5^2x = 150
25x + 1 + 25x = 150
50x + 1 = 150
50x = 149
x = 2.98
5^2x + 1 - 5^2x = ?
5^2(2.98) + 1 - 5^2(2.98) = ?
25(2.98) + 1 + 25(2.98) = ?
74.5 + 1 + 74.5 = ?
149 + 1 = ?
150 = ?
The value of x is 2.98
What is an equation?An equation is a mathematical statement that shows that two mathematical expressions are equal.
Given an equation, 5^2x+1-5^2x=150
5^2x + 1 - 5^2x = 150
25x + 1 + 25x = 150
50x + 1 = 150
50x = 149
x = 2.98
For more references on equation, click;
https://brainly.com/question/10413253
#SPJ2
snicker fun size 10.59oz the cost is 3.89 what is the price per ounce.

Answers
Step 1
Given;
\(\begin{gathered} \text{ Candy bars = 10.59oz} \\ \text{Cost}=\text{\$}3.89 \end{gathered}\)Required; To find the price per ounce
Step 2
State the ratio that can be used to find the price per ounce of the candy bars.
\(\begin{gathered} \frac{\text{\$}3.89}{x}=\frac{10.59oz}{1oz} \\ 3.89\times1=10.59x \\ x=\frac{3.89}{10.59} \\ x=\text{\$}0.3673276676 \\ x\approx\text{\$0.37} \\ \text{That is approxi}mately\text{ 37 cents} \end{gathered}\)in terms of a dot product, give a definition of what it means for two vectors in r4 to be orthogonal.
Answers
Two vectors in ℝ⁴ are orthogonal if their dot product is zero.
Two vectors in ℝ⁴ are said to be orthogonal if their dot product is zero. The dot product of two vectors measures the similarity or alignment between them. When the dot product is zero, it signifies that the vectors are perpendicular to each other and do not share any common direction.
Geometrically, orthogonality between two vectors in ℝ⁴ means that they are linearly independent and span different directions in four-dimensional space. It implies that there is no projection of one vector onto the other, and they are completely perpendicular to each other.
The concept of orthogonality is fundamental in many areas of mathematics, physics, and engineering. In linear algebra, orthogonal vectors play a crucial role in defining orthogonal bases and orthogonal projections. They also have applications in vector calculus, where they are used to define gradients and normal vectors. In physics, orthogonal vectors are relevant in studying forces, velocities, and geometric transformations. Overall, understanding orthogonality is essential for analyzing vector relationships and geometric properties in multi-dimensional spaces.
To know more about dot product of vectors, visit:
https://brainly.com/question/33811285
#SPJ11
A spherical hot-air balloon has a diameter of 55 feet. when the balloon is inflated, the radius increases at a rate of 1.5 feet per minute. approximately how long does it take to inflate the balloon to two-thirds of its maximum volume? use π = 3.14 and v = four-thirds pi r cubed. 16 minutes 18 minutes 23 minutes 26 minutes
Answers
Time taken to inflate the balloon to two-thirds of its maximum volume is 16 minutes.
Given the diameter of the balloon = 55 ft
Let r be the radius of the balloon. Then r = 55/2 = 27.5 ft
Rate of change of radius = 1.5 ft/min.
The maximum volume of the balloon = \(\frac{4}{3}\pi r^3\) = \(\frac{4}{3}\times3.14\times 27.5^3\)
= 87069.583 \(ft^3\)
Two- thirds of the volume = (2/3) x 87069.583 = 58046.389 \(ft^3\)
Let R be the radius of the balloon with two-thirds of its maximum volume.
Then, \(\frac{4}{3}\pi R^3\) = 58046.389
⇒ \(R^3=\frac{3}{4\times3.14}\times 58046.389\) = 13864.583
⇒ \(R=13864.583^\frac{1}{3}\)
⇒ R = 24.023 ft
Now time taken to inflate balloon to the two-third of the maximum volume = 24.023/1.5 = 16 minutes approximately.
Learn more about the Volume of a sphere at https://brainly.com/question/22716418
#SPJ4
Answer:
A) 16 minutes
Step-by-step explanation:
Hope this helps! Pls give brainliest!

Please help I need the answer soon!!!!!!

Answers
Answer:
The measure of angle two is 47 degrees (first triangle), and the measure of angle four is 42 degrees (second angle)
Step-by-step explanation:
Remember that all triangles have a full measurement of 180 degees.
Since measure one is is 65 degrees, we need to add 65 and 68, which is 133 degrees.
Now we subtract 180 - 133 = 47.
The measure of angle two is 47 degrees.
Since the angle of measure three is 89 degrees, we need to add 89 + 49, which is 138 degrees.
180 - 138 = 42.
What is the value of x

Answers
Answer:
The value of x is 138
20. For the data in the following sample: 10, 6, 8, 6, 5 a. Find the mean and the standard deviation. b. Now change the score of X 5 10 to X 5 0, and find the new mean and standard deviation. c. Describe how one extreme score influences the mean and standard deviation.
Answers
By replacing the extreme score of 10 with 0, the mean and standard deviation will be affected and will become 5 and 2.68 and the original mean and standard deviation were 7 and 1.79 respectively.
a. Mean: To find the mean, sum all the scores and divide by the number of scores. For the given data (10, 6, 8, 6, 5), the sum is 35, and since there are five scores, the mean is 35/5 = 7.
Standard Deviation: To find the standard deviation, we first calculate the deviations of each score from the mean. The deviations are (10-7), (6-7), (8-7), (6-7), and (5-7), which are 3, -1, 1, -1, and -2, respectively.
Then, square each deviation, resulting in 9, 1, 1, 1, and 4. The average of these squared deviations is (9+1+1+1+4)/5 = 16/5 = 3.2. Finally, take the square root of the average squared deviation to get the standard deviation, which is √3.2 ≈ 1.79.
b. Changing the score of 10 to 0, the new data set becomes (0, 6, 8, 6, 5).
New Mean: The sum of the new data set is 0+6+8+6+5 = 25, and since there are still five scores, the new mean is 25/5 = 5.
New Standard Deviation: Following the same steps as before, the deviations from the new mean are (-5, 1, 3, 1, 0), which result in squared deviations of 25, 1, 9, 1, and 0.
The average of these squared deviations is (25+1+9+1+0)/5 = 36/5 = 7.2. Taking the square root of the average squared deviation gives the new standard deviation, which is √7.2 ≈ 2.68.
c. One extreme score, such as the initial score of 10, has a significant impact on both the mean and standard deviation. The mean represents the central tendency of the data, and when an extreme score is present, it pulls the mean towards it.
In this case, the mean decreased from 7 to 5 when the extreme score was changed to 0. The standard deviation measures the spread or variability of the data, and extreme scores can widen the spread.
Thus, by replacing the extreme score of 10 with 0, the standard deviation increased from 1.79 to 2.68, indicating a greater dispersion in the data.
To learn more about mean click here: brainly.com/question/30112112
#SPJ11
Suppose that you had option of working at one of the three possible jobs. The first job was paying $10, on the second job you would get $13 and the third job would pay $15. If you decide to take time off and go to a dinner party your friend is hosting. Your opportunity cost of this evening would be nothing as you do not have to pay for dinner. $10. $13. $15. $38.
Answers
The opportunity cost of attending the dinner party would be $15, as it represents the potential earnings from the highest-paying job option among the three.
The opportunity cost refers to the value of the next best alternative that you forego when making a decision. In this scenario, if you choose to attend the dinner party instead of working, you are giving up the potential earnings from one of the job options.
The highest-paying job among the three options is the third job, which pays $15. Therefore, the opportunity cost of attending the dinner party would be $15. This means that by choosing to go to the party, you are forfeiting the opportunity to earn $15.
It is important to consider opportunity costs when making decisions, as they reflect the value of the alternatives that are being sacrificed. In this case, even though you may not have to pay for the dinner at the party, the opportunity cost is still present in terms of the potential income that could have been earned if you had chosen to work instead.
To know more about opportunity cost:
https://brainly.com/question/26003725
#SPJ4
what are the minimum and maximum numbers of elements in a heap of height h?
Answers
In a heap, the height is defined as the number of edges on the longest path from the root to a leaf node. The height of a heap with n elements is at most log₂(n+1).
To find the minimum and maximum numbers of elements in a heap of height h, we can use the formula:
The minimum number of elements in a heap of height h is 2^h (a complete binary tree of height h with the minimum number of nodes).
The maximum number of elements in a heap of height h is 2^(h+1) - 1 (a complete binary tree of height h with the maximum number of nodes).
Therefore, the minimum and maximum numbers of elements in a heap of height h are:
Minimum: 2^h
Maximum: 2^(h+1) - 1
Note that not all values of h are valid heap heights. A heap must be a complete binary tree, so its height can only take on values that satisfy the formula: \(h < = log₂(n+1),\)where n is the number of elements in the heap.
Learn more about height here:
https://brainly.com/question/10726356
#SPJ11
I NEED HELP ASAP ! THIS IS FOR A PAST DUE QUIZ. THEY ARE GIVING ME ONE MORE CHANCE
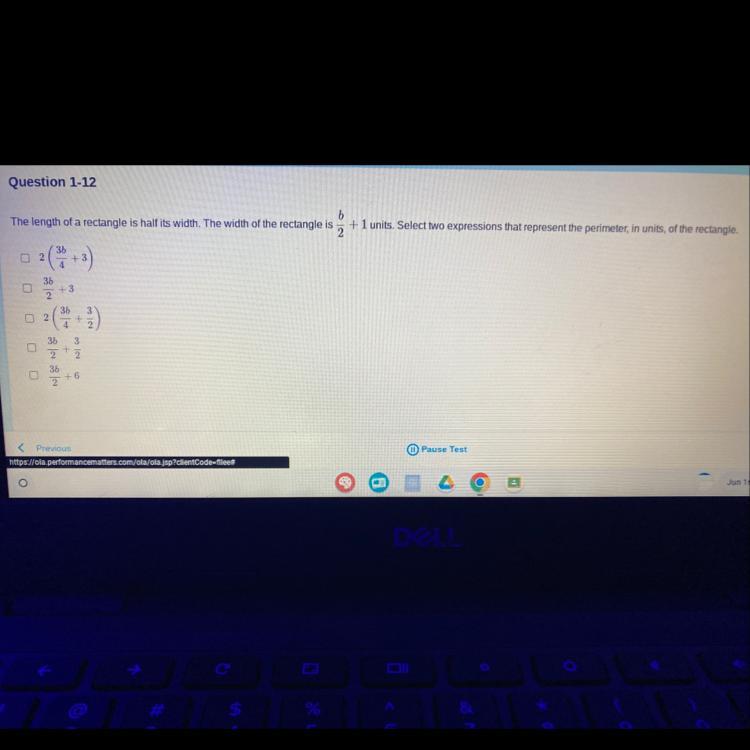
Answers
Answer:
3b/2 + 3
Step-by-step explanation:
The formula to calculate perimeter of rectangle is 2l + 2w
The length is half the width so length is 1/2 (b/2 +1), which when simplified is b/4 + 1/2
Using the formula to calculate perimeter you can substitute and calculate
p= 2l + 2w
p= 2(b/4 + 1/2) + 2(b/2 + 1)
p= 2b/4 +2/2 + 2b/2 +2
p= 1/2b + 1 + b + 2
p= 3/2b + 3
Simplified it's 3b/2 +3
Which of the following is the graph of y=-4 square root x

Answers
In the second graph, these points are located. As a result, the second graph is the function's correct graph.
what is function ?In mathematics, the term "linear function" refers to two different but related ideas. In calculus and related fields, a quadratic variable of grade 0 or 1 is a linear function if its graph is a direct line. A straight line on a reference system is a representation of a linear function. For instance, the linear function y = 3x - 2 is a straight line just on coordinate plane, hence it is a linear function. Since f(x) may be connected to y, the function can be represented by f(x) = 3x - 2.
given
The function provided is
This function is defined for any x values that are positive, including 0.
The radical expression x has a constant positive value. Given that is a function, it is always negative.
At x=0, = 0
At x=1, = -4
At x=4, = -8
This indicates that the graph of the specified function traveling through the points (0,0), (1,-4) and (4,-8).
In the second graph, these points are located. As a result, the second graph is the function's correct graph.
To know more about linear function visit:
https://brainly.com/question/29205018
#SPJ1
Suppose h is a function such that h(1) = -3, h'(1) = 3, h''(1) = 4, h(5) = 5, h'(5) = 7, h''(5) = 12, and h'' is 5 • f.° continuous everywhere. Evaluate h'' (u) du.
Answers
the value of the integral ∫[1, 5] h''(u) du is 4.
The Fundamental Theorem of Calculus states that if F(x) is an antiderivative of a function f(x) on an interval [a, b], then the integral of f(x) from a to b is equal to F(b) - F(a).In this case, we are given that h'' is 5 • f.° continuous everywhere. Therefore, we can denote h''(u) as 5f(u). To evaluate the integral h''(u) du, we need to find an antiderivative of 5f(u).
Since h'' is 5 • f.° continuous everywhere, we know that h'(u) is an antiderivative of 5f(u). Given the information h'(1) = 3 and h'(5) = 7, we can apply the Fundamental Theorem of Calculus:
∫[1, 5] 5f(u) du = [h'(u)]|[1, 5]
= h'(5) - h'(1)
= 7 - 3
= 4
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
In a large population, 68% of the people have been vaccinated. If 4 people are randomly selected, what is the probability that at least one of them has been vaccinated? Round your answer to three decimal places. Hint: If 4 are randomly selected, then the probability that none of the 4 people has not been vaccinated is (0.32)
Answers
The probability that at least one person is vaccinated is 1 - (0.32), which is equal to 0.68.
To calculate the probability that at least one out of four randomly selected people has been vaccinated, we can use the complementary probability approach. The complementary probability is equal to 1 minus the probability of the event not occurring.
Given that 68% of the population has been vaccinated, the probability that an individual has been vaccinated is 0.68. Therefore, the probability that an individual has not been vaccinated is 1 - 0.68, which is 0.32.
Using the hint provided, we can calculate the probability that none of the four people have been vaccinated as (0.32) raised to the power of 4 since the events are independent and the probability of each event is 0.32.
So, the probability that at least one person is vaccinated is equal to 1 minus the probability that none of the four people are vaccinated. Thus, the probability is 1 - (0.32) = 0.68.
In summary, the probability that at least one out of four randomly selected people has been vaccinated is 0.68, given that 68% of the population has been vaccinated. This is calculated by subtracting the probability that none of the four people are vaccinated from 1.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
math hw 1
The Normal Distribution
pls help me with my homework!!
thanks,

Answers
Using the normal distribution, it is found that the desired measures are given by:
a. Z = -0.67.
b. X = 2.2.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean \(\mu\) and standard deviation \(\sigma\) is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.In item a, we have that \(X = 36, \mu = 40, \sigma = 6\), and want to find Z, hence:
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{36 - 40}{6}\)
Z = -0.67.
In item b, we have that \(\mu = 1.3, \sigma = 0.6, Z = 1.5\), and want to find X, hence:
\(Z = \frac{X - \mu}{\sigma}\)
\(1.5 = \frac{X - 1.3}{0.6}\)
X - 1.3 = 0.6 x 1.5
X = 2.2.
More can be learned about the normal distribution at https://brainly.com/question/24663213
#SPJ1