given the function h(x)=3x+1 and g(x)= x/3 find
a) h^-1 (x)
b)gh^-1 (7)
Answers
Answer:
h‐¹(x)= (x-1)/3
To do this switch the x and y variables in this case it would be x=3y+1 and rearrange to get the y alone
gh‐¹(7)=(x-1)/9=(7-1)/9=2/3
For this section substitutethe x in the g(x) equation with h-¹(x) and then simplify to get your final expression then substitute 7 in place of x to get your integer answer
Hope it's clear, cheers!
Related Questions
1>-1=-3>-5 this property is called?
Answers
Answer:
linear inequation with 1 variable
Calculate the median of the following data set: {2, 22, 8, 6, 19, 15, 5, 12} 6 19 10 2
Answers
Answer:
10
Step-by-step explanation:
median is the middle number
these numbers in order are 2, 5, 6, 8, 12, 15, 19, 22 and the middle numbers are 8 and 12
to ind the middle number of those two numbers, you find the mean (averge) of those numbers
mean: 8+12=20/2=10
lmk if its right!
Accuracy is how _______ a measurement is to the expected value'
Answers
Answer:
Accuracy is how close a measured value is to an accepted value. Precision is how close measurements are to one another. To make measurements, you have to evaluate both the accuracy and the precision to get a correct value.
Which expression represents the phrase 5+ the quotient of 12. 8 and 3. 2
Answers
Expression 5 + (12.8 ÷ 3.2) represents the phrase 5 + the quotient of 12. 8 and 3. 2 and option (a) is the correct answer.
Expressions refer to a phrase with at least two numbers or variables with any mathematical operations such as addition, exponents, etc. x - 6, 9 + 4y, and 6a are all examples of mathematical expressions.
Equations refer to a sentence when two expressions are equated with the help of '='. x - 6 = 6a is an example of an equation.
In phrase 5+ the quotient of 12. 8 and 3. 2
We divide the phrase into different mathematical operations.
The first operation is of addition with 5, we can write the beginning as 5 + ...
The next operation is division in the phrase the quotient of 12. 8 and 3. 2 which is added to the expression and we get 5 + (12.8 ÷ 3.2)
And we get our answer.
Learn more about Expressions:
https://brainly.com/question/25968875
#SPJ4
The complete question might be :
Which expression represents the phrase 5+ the quotient of 12. 8 and 3. 2?
a. 5 + (12.8 ÷ 3.2)
b. 5 - (12.8 + 3.2)
c. 5 + (12.8 * 3.2)
d. none of the above
HELPP EASY MATH FOR Y GUYS IM 5 GRADE

Answers
Answer:
Step-by-step explanation:
for number 9.) 9r-45
PLEASE HELP I WILL MARK YOU BRAINLIEST.
Janet is comparing the prices of bottled drinks. She finds one bottle of water that costs $1.92 and contains 12 ounces. She then finds one bottle of soda that costs $2.40 and contains 16 ounces. Which bottle costs less per ounce?
Answers
Answer:
1.92
Step-by-step explanation:
2.40 is more than 1.92
Solve the following question

Answers
Considering that a fraction is not defined when the denominator is zero, the equation is not defined for an angle of 90º.
When is a fraction not defined?A fraction is not defined when the denominator is zero.
In this problem, the expression is given by:
cos(θ)/(1 - sin(θ)) + cos(θ)/(1 + sin(θ)) = 4.
The denominators are zero in two cases:
1 - sin(θ) = 0 -> sin(θ) = 1 -> θ = 90º.1 + sin(θ) = 0 -> sin(θ) = -1 -> θ = 270º.Hence the equation is not defined for an angle of 90º.
More can be learned about not defined fractions at https://brainly.com/question/16948935
#SPJ1
someone please help I CAN'T SOLVE THIS I NEED TO FIND M AND Z
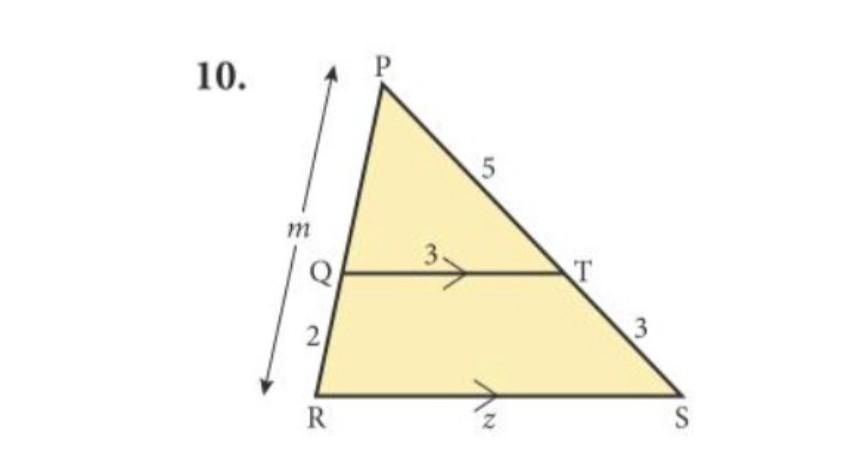
Answers
Answer:
m = \(\frac{16}{3}\) , z = \(\frac{24}{5}\)
Step-by-step explanation:
Δ PQT and Δ PRS are similar ( by AA postulate ), so the ratios of corresponding sides are equal, that is
\(\frac{PQ}{PR}\) = \(\frac{PT}{PS}\) , substitute values
\(\frac{m-2}{m}\) = \(\frac{5}{8}\) ( cross- multiply )
8(m - 2) = 5m ← distribute parenthesis on left side
8m - 16 = 5m ( subtract 5m from both sides )
3m - 16 = 0 ( add 16 to both sides )
3m = 16 ( divide both sides by 3 )
m = \(\frac{16}{3}\)
and
\(\frac{QT}{RS}\) = \(\frac{PT}{PS}\) , substitute values
\(\frac{3}{z}\) = \(\frac{5}{8}\) ( cross- multiply )
5z = 24 ( divide both sides by 5 )
z = \(\frac{24}{5}\)
The cube of the sum of a number and 5.
Answers
Answer:
\((x+5)^{3}\)
Step-by-step explanation:
Hope this helps
The expression for the word problem is ( x + 5 )².
What is an expression?Expression in maths is defined as the collection of numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
Numbers (constants), variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.
The given word problem is the cube of the sum of a number and 5. The expression will be formed as below:-
Let the unknown number be x.
E = ( x + 5 )²
Therefore, the expression for the word problem is ( x + 5 )².
The complete question is given below:-
The cube of the sum of a number and 5. Write the mathematical expression.
To know more about an expression follow
https://brainly.com/question/723406
#SPJ2
5 and 3/4 divided by 1 and 1/2
Answers
Answer:Exact Form:
23/6
Decimal Form:
3.83
Mixed Number Form:
3 5/6
what is the value of 12x^-3 y-1 for x=-1 and y=5
A.-12/5
B.-180
C.-60
D.-5/12
Answers
Expressions are mathematical statements represented with the variables
The value of 12x^-3 y-1 for x=-1 and y=5 is - 12/5
How to determine the value of the variableThe expression is given as:
\(12x^{-3} y^{-1}\)
When x = -1, the expression becomes
\(12 * -1^{-3} y^{-1}\)
Evaluate the exponent
\(- 12 y^{-1}\)
When y = 5, the expression becomes
\(- 12 * 5^{-1}\)
Evaluate the exponent
- 12/5
Hence, the value of 12x^-3 y-1 for x=-1 and y=5 is - 12/5
Read more about expressions at:
https://brainly.com/question/723406
In 2020, a total of 9559 Nissan Leafs were sold in the US. For the 12-month period starting January 2020 and ending December 2020, the detailed sales numbers are as follows: 651, 808, 514, 174, 435, 426, 687, 582, 662, 1551, 1295 and 1774 units.
before the Nissan plant in Smyrna, Tennessee, started to produce the Nissan Leaf they were imported from Japan. Although cars are now assembled in the US, some components still imported from Japan. Assume that the lead time from Japan is one weeks for shipping. Recall that the critical electrode material is imported from Japan. Each battery pack consists of 48 modules and each module contains four cells, for a total of 192 cells. Assume that each "unit" (= the amount required for an individual cell in the battery pack) has a value of $3 and an associated carrying cost of 30%. Moreover, assume that Nissan is responsible for holding the inventory since the units are shipped from Japan. We suppose that placing an order costs $500. Assume that Nissan wants to provide a 99.9% service level for its assembly plant because any missing components will force the assembly lines to come to a halt. Use the 2020 demand observations to estimate the annual demand distribution assuming demand for Nissan Leafs is normally distributed. For simplicity, assume there are 360 days per year, 30 days per month, and 7 days per week.
(a) What is the optimal order quantity?
(b) What is the approximate time between orders?
Answers
(a)The optimal order quantity is 4609 units.
(b)The time between orders is 1.98 months.
To determine the optimal order quantity and the approximate time between orders, the Economic Order Quantity (EOQ) model. The EOQ model minimizes the total cost of inventory by balancing ordering costs and carrying costs.
Optimal Order Quantity:
The formula for the EOQ is given by:
EOQ = √[(2DS) / H]
Where:
D = Annual demand
S = Cost per order
H = Holding cost per unit per year
calculate the annual demand (D) using the 2020
sales numbers provided:
D = 651 + 808 + 514 + 174 + 435 + 426 + 687 + 582 + 662 + 1551 + 1295 + 1774
= 9559 units
To calculate the cost per order (S) and the holding cost per unit per year (H).
The cost per order (S) is given as $500.
The holding cost per unit per year (H) calculated as follows:
H = Carrying cost percentage × Unit value
= 0.30 × $3
= $0.90
substitute these values into the EOQ formula:
EOQ = √[(2 × 9559 × $500) / $0.90]
= √[19118000 / $0.90]
≈ √21242222.22
≈ 4608.71
Approximate Time Between Orders:
To calculate the approximate time between orders, we'll divide the total number of working days in a year by the number of orders per year.
Assuming 360 days in a year and a lead time of 1 week (7 days) for shipping, we have:
Working days in a year = 360 - 7 = 353 days
Approximate time between orders = Working days in a year / Number of orders per year
= 353 / (9559 / 4609)
= 0.165 years
Converting this time to months:
Approximate time between orders (months) = 0.165 × 12
= 1.98 months
To know more about quantity here
https://brainly.com/question/14581760
#SPJ4
mentum.com
Lxpre3310113, 1931
ial Expressions: Mastery Test
5
Drag each tile to the correct box.
Using the order of operations, what are the steps for solving this expression?
40+8+32+(15-7) × 2
Arrange the steps in the order in which they are performed.
3²
5+9
40+8
14+ 16
8x2
KNOW
15-7
Answers
The order in which they performed be
14 + 16 . . . . add 5 + 9
30 . . . . . . . add 14 + 16
What is meant by expression?A mathematical expression is a phrase that has a minimum of two numbers or variables and at least one mathematical operation. There are four possible math operations here: addition, subtraction, multiplication, and division.
Given: 40/8 + 3² + (15 - 7) × 2
The order of operations instructs you to begin by assessing parenthesized expressions. This is done by deducting 7 from 15.
40/8 + 3² + 8 × 2 . . . . (15 - 7) = 8
Then you evaluate exponential terms.
40/8 + 9 + 8 × 2 . . . . . 3² = 9
Next, multiply and divide from left to right. In this case, division comes before multiplication.
5 + 9 + 8 × 2 . . . . . divide 40/8 = 5
5 + 9 +16 . . . . . . multiply 8 × 2 = 16
The order in which they performed be
14 + 16 . . . . add 5 + 9
30 . . . . . . . add 14 + 16
The complete question is:
Using the order of operations, what are the steps for solving this expression?
40/8+3^2+(15-7)*2
Arrange the steps in the order in which they are performed.
To learn more about expression refer to:
https://brainly.com/question/1859113
#SPJ1
What is the least integer value that satisfies the inequality 2x – 7 ≥ 3?
Answers
Answer:
5
Step-by-step explanation:
2x - 7 + 7 > 3 + 7
2x/2 > 10/2
x > 5
(my device doesn't have the sign for greater than or equal to so imagine i used it)
Answer:
9
Step-by-step explanation:
2^(7–7) =1 1 ≥ 3? No
2^(8–7) =2 2 ≥ 3? No
2^(9–7) =4 4 ≥ 3? Yes
A ring is reduced to £840. This is a saving of 40% of the original price. What was the original price
Answers
The answer is 1400, good luck
An architect wants to reduce a set of blueprints to make a portable set for easy access. The original dimensions of the blueprints are 24 inches by 36 inches. She reduces the blueprints by a scale factor of 13. She then decides that the reduced blueprints are a little too small and enlarges them by a scale factor of 1.25. Will the final image fit in a similar portfolio with an area of 160 square inches? Justify your response.
Answers
The final image will fit in a similar portfolio with an area of 160 square inches.
How to obtain the area of a rectangle?To obtain the area of a rectangle, you need to multiply its length by its width. The formula for the area of a rectangle is:
Area = Length x Width.
The dimensions for this problem are given as follows:
24 inches, 36 inches.
With the reduction with a scale factor of 1/3, the dimensions are given as follows:
8 inches, 12 inches.
With the enlargement by a factor of 1.25, the dimensions are given as follows:
10 inches and 15 inches.
Hence the area is given as follows:
15 x 10 = 150 square inches.
As the area of 150 square inches is less than 160 square inches, the final image will fit in a similar portfolio with an area of 160 square inches.
More can be learned about the area of a rectangle at brainly.com/question/25292087
#SPJ1
8t+1+(−4t)+(−6) ?????????????
Answers
8t + 1 - 4t - 6
Combining like terms:
4t - 5
if triangle dgh is congruent to triangle def find the value of x

Answers
Answer:
x = 25
Step-by-step explanation:
\( \triangle DGH\sim\triangle DEF... (given) \)
\( \frac{DG}{DE} =\frac{GH}{EF} \)
\( \frac{52}{91} =\frac{x+3}{2x-1} \)
\( \frac{4}{7} =\frac{x+3}{2x-1} \)
4(2x - 1) = 7(x + 3)
8x - 4 = 7x + 21
8x - 7x = 21 + 4
x = 25
There were 3,260 visitors to a county fair on Friday. On Saturday the number of visitors to the fair increased by 15%. Fair organizers had projected a 20% increase in attendance on Saturday. By how many visitors did Saturday's actual attendance fall short of the projected attendance?
Answers
Answer:
163
Step-by-step explanation:
Given the following :
Number of visitors on Friday = 3,260
Number increased by 15% on Saturday
Projected percentage increase on Saturday = 20%
Actual percentage increase in number of visitors = 15%
Number of visitors on Saturday :
(100 + 15)% × 3260
115% * 3260
(115/100) * 3260
= 3749 visitors
Projected percentage increase = 20%
Projected number:
((100 + 20)% * 3260
120% * 3260
(120/100) * 3260
= 3912
Difference : (3912 - 3749) = 163
PLEASE ITS ALREADY LATE AND I NEED TO TURN IT TODAY
Example 1 Fatima works as an intern at a construction company earning $10 per hour. Her office is open 8
hours per day, 5 days a week. Analyze Fatima's potential earnings for the 12 weeks she interns at the
company this summer.
A. Write a function rule to model
the situation
B. Identify the independent
variable
C. Identify the dependent
variable
f(x) =
Answers
Answer:
4800
Step-by-step explanation:
I attached a picture of the work.
We need to made a function that will help us solve this
f(x)=dx; d = $ per hour, x = # of hours
step 1) identify d (in this case, the money made per hour) which = 10
f(x)=10x
step 2) identify x (# of hours total) which = 480
f(x)=10(480)
step 3) solve the equation
f(x)=4800
independent variable:
the number of hours
dependant variable:
the amount of money made after 12 weeks

How do you write in slope intercept with only the rate of change and one point. Like rate of change is -5 and the point is (3,0)
Answers
Answer:
A linear equation in the slope-intercept form is written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
Now, we know that the rate of change (the slope) is -5
Then we just replace a by -5
y = -5*x + b
Now we also know that this line passes through a point, and the point is (3, 0)
This means that the point (3, 0) is a solution for the line equation, so when x = 3, we also have y = 0.
Replacing these values in our equation we get:
0 = -5*3 + b
0 = -15 + b
15 = b
Now we know the value of b, so we can replace it in the line equation to get:
y = -5*a + 15
Which is the complete equation of the line.
The probability of a student spending time reading is 0.59, and the probability of a student doing well on an exam and spending time reading is 0.58. What is the probability of a student doing well on an exam given that the student spends time reading
Answers
The probability of a student doing well on an exam given that they spend time reading is approximately 0.983 or 98.3%.
To calculate the probability of a student doing well on an exam given that the student spends time reading, we need to use conditional probability.
Let's denote:
P(R) as the probability of a student spending time reading (P(R) = 0.59),
P(E) as the probability of a student doing well on an exam (P(E)),
P(E|R) as the probability of a student doing well on an exam given that they spend time reading (P(E|R) = 0.58).
The formula for conditional probability is:
P(E|R) = P(E and R) / P(R).
Given that P(E and R) = 0.58 (the probability of a student doing well on an exam and spending time reading) and P(R) = 0.59 (the probability of a student spending time reading), we can substitute these values into the formula:
P(E|R) = 0.58 / 0.59 = 0.983.
Therefore, the probability of a student doing well on an exam given that the student spends time reading is approximately 0.983 or 98.3%.
To know more about probability, visit:
https://brainly.com/question/29120105
#SPJ11
One car travels 6 mph slower than another car. They both start at the same place but travel in the opposite directions. After 4 hours and 20 min, they are 260 miles apart. How fast is each car traveling?
Answers
Answer:
27mph
Step-by-step explanation:
Let's assume the speed of the first car is x mph. Since the second car is traveling 6 mph slower, its speed would be (x - 6) mph.
To find out how far each car has traveled, we can use the formula: distance = speed × time.
For the first car:
Distance traveled by the first car = speed of the first car × time
d₁ = x mph × (4 hours + 20 minutes)
Since we need to work with a single unit of time, let's convert 20 minutes to hours:
20 minutes = 20/60 = 1/3 hours
Substituting the values:
d₁ = x mph × (4 + 1/3) hours
d₁ = x mph × (13/3) hours
d₁ = (13x/3) miles
For the second car:
Distance traveled by the second car = speed of the second car × time
d₂ = (x - 6) mph × (4 hours + 20 minutes)
d₂ = (x - 6) mph × (13/3) hours
d₂ = (13/3)(x - 6) miles
Since they are traveling in opposite directions, the sum of their distances is equal to the total distance between them:
d₁ + d₂ = 260 miles
Substituting the expressions for d₁ and d₂:
(13x/3) + (13/3)(x - 6) = 260
To simplify the equation, let's multiply both sides by 3 to get rid of the denominators:
13x + 13(x - 6) = 780
13x + 13x - 78 = 780
26x - 78 = 780
26x = 780 + 78
26x = 858
x = 858/26
x ≈ 33
The speed of the first car is approximately 33 mph. Substituting this value back into the equation for the speed of the second car:
Speed of the second car = x - 6 ≈ 33 - 6 ≈ 27 mph
Therefore, the first car is traveling at approximately 33 mph, and the second car is traveling at approximately 27 mph.
Sakura solved a fraction division problem using the rule "multiply by the reciprocal." Look at her work. 7 ÷ 2/ 5 1/ 7 × 2/ 5 = 2/35 Did she solve the problem correctly?
Answers
Answer:
D. No. She multiplied with the reciprocal of the dividend instead of the reciprocal of the divisor.
Step-by-step explanation:
A. Yes. She solved the problem correctly.
B. No. She multiplied the dividend by the divisor instead of finding the reciprocal.
C. No. She multiplied the denominators instead of finding a common denominator.
D. No. She multiplied with the reciprocal of the dividend instead of the reciprocal of the divisor.
Her workings
7 ÷ 2/ 5
=1/ 7 × 2/ 5
= 2/35
Dividend=7
Divisor=2/5
The correct working
7 ÷ 2/ 5
=7 × 5/2
=35/2
Answer:
D
Step-by-step explanation:
I got an 100% on the quiz I took with this question :)
Hope I could help good luck on passing!!
Brian invests £990 into his bank account. He receives 2% per year simple interest. How much
will Brian have after 4 years?
Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \£990\\ r=rate\to 2\%\to \frac{2}{100}\dotfill &0.02\\ t=years\dotfill &4 \end{cases} \\\\\\ A=990[1+(0.02)(4)]\implies A=990(1.02)(4)\implies A=4039.2\)
Solve the system of equations.
2x-3x=21 and -6x+2y=7
Answers
Answer:
(-21, -59.5)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Algebra I
Solving systems of equations using substitution/eliminationStep-by-step explanation:
Step 1: Define Systems
2x - 3x = 21
-6x + 2y = 7
Step 2: Solve for x
2x - 3x = 21
Combine like terms: -x = 21Isolate x: x = -21Step 3: Solve for y
Define equation: -6x + 2y = 7Substitute in x: -6(-21) + 2y = 7Multiply: 126 + 2y = 7Isolate y term: 2y = -119Isolate y: y = -59.5The lifetime of a certain type of automobile tire (in thousands of miles) is normally distributed with mean μ = 39 and standard deviation σ = 6. Use the TI-84 Plus calculator to answer the following.
(a) Find the 19th percentile of the tire lifetimes.
(b) Find the 71st percentile of the tire lifetimes.
(c) Find the first quartile of the tire lifetimes.
(d) The tire company wants to guarantee that its tires will last at least a certain number of miles. What number of miles (in thousands) should the company guarantee so that only 2% of the tires violate the guarantee?Round the answers to at least two decimal places.
Answers
The TI-84 Plus calculator can be used to find various percentiles and guarantee values for a certain type of automobile tire. The 19th percentile of tire lifetimes is approximately 35.38 thousand miles. The 71st percentile is approximately 42.85 thousand miles. The first quartile, which represents the 25th percentile, is approximately 37.07 thousand miles. To ensure that only 2% of the tires violate the guarantee, the tire company should guarantee a minimum of approximately 31.35 thousand miles.
To find the percentiles and guarantee values using the TI-84 Plus calculator, we can utilize the normal distribution function. Given that the lifetime of the automobile tires is normally distributed with a mean (μ) of 39 thousand miles and a standard deviation (σ) of 6 thousand miles, we can apply these values to the calculator.
(a) To find the 19th percentile, we input the following command: invNorm(0.19, 39, 6). The calculator will provide an output of approximately 35.38 thousand miles.
(b) For the 71st percentile, we use the command: invNorm(0.71, 39, 6). The calculator will yield an approximate value of 42.85 thousand miles.
(c) The first quartile, representing the 25th percentile, can be obtained by entering: invNorm(0.25, 39, 6). The calculator will give an output of approximately 37.07 thousand miles.
(d) To determine the guarantee value for which only 2% of the tires violate the guarantee, we use the command: invNorm(0.02, 39, 6). The calculator will provide an approximate value of 31.35 thousand miles.
These calculations give us the requested percentiles and guarantee value for the tire lifetimes, rounded to at least two decimal places.
Learn more about standard deviation here: https://brainly.com/question/23986929
#SPJ11
Line ℓ has equation y=7. Find the distance between ℓ and the point D(-5,-7). Round your answer to the nearest tenth.
Answers
The required distance of the point from the line is given as 2 units.
Given that,
Line ℓ has equation y=7. Find the distance between ℓ and point D(-5,-7).
The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
here,
For the line l y = 7, the distance from the point D(-5, -7) is given as,
D =| l |/ |l|
D = y - 7 / √y²
Now put y = -7 in the above equation,
D = |-7 - 7 | / √7²
D = 14 / 7
D = 2
Thus, the required distance of the point from the line is given as 2 units.
Learn more about lines here:
https://brainly.com/question/22567337
#SPJ1
A stone pyramid in Egypt has a square base that measures 154 m on each side. The height is 91 m. What is
the volume of the pyramid?
Answers
Answer:
14014
Step-by-step explanation:
base of stone pyramid=154
height=91
b×h
154×91=4014
PLS HELP ASAP (Brainliest answer if it's right)
The width of a rectangle measures (8p+5) centimeters, and its length measures (4p+4) centimeters. Which expression represents the perimeter, in centimeters, of the rectangle?
1. 24p+18
2. 8+13p
3. 9+12p
4. 26p+16
Thx if u help>3
Answers
Answer:
1. 24p + 18
Step-by-step explanation:
One of the formulas used to find the perimeter of a rectangle is:
P = 2(l + w)
Where P is the perimeter, l is the length, and w is the width. We can substitute in the given values:
P = 2[(4p + 4) + (8p + 5)]
Now we can combine the like terms:
P = 2[12p + 9]
And simplify:
P = 24p + 18
This is the same as option 1.