Given the point and the slope, write the function in point-slope form:
(2, -5); m = 2/3
plz help

Answers
Answer:
3rd option
Step-by-step explanation:
=)
Related Questions
Mr. Agan went on a hike in the morning and
started at an elevation of 15 feet below sea
level. At noon he had reached an elevation
of 3,540 feet. What was his change in
elevation?
Answers
Answer:
Step-by-step explanation:
I’m not sure but I think division 3,540/15=236
I NEED ANSWERS *QUICK!!!!*
Q: What is the constant of proportionality that relates number of chairs, y, to the number of tables, x?

Answers
In linear equation, 12 is the constant of proportionality that relates number of chairs, y, to the number of tables, x.
What in mathematics is a linear equation?
An algebraic equation with simply a constant and a first-order (linear) component, such as y=mx+b, where m is the slope and b is the y-intercept, is known as a linear equation. Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.
Number of tables, x = 3
number of chairs , y = 36 = 36/3 = 12
Row 2 says the same thing = 72/6 = 12
Row 2 says the same thing = 108/9 = 12
Learn more about linear equation
brainly.com/question/11897796
#SPJ1
Find an equation for the line tangent to the graph of the given function at the indicated point. 8 3) f(x): () = at at (4,2) X 1 4) f(x)=x2-x at (4, 12)
Answers
(a) tangent line to the graph of f(x) = x^3 at the point (4,2).
(b) equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12).
(a) To find the equation of the tangent line to the graph of f(x) = x^3 at the point (4,2), we need to find the slope of the tangent line at that point. We can do this by taking the derivative of f(x) with respect to x and evaluating it at x = 4. The derivative of f(x) = x^3 is f'(x) = 3x^2. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Once we have the slope, we can use the point-slope form of a linear equation to write the equation of the tangent line.
(b) Similarly, to find the equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12), we differentiate f(x) to find the derivative f'(x). The derivative of f(x) = x^2 - x is f'(x) = 2x - 1. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Using the point-slope form, we can write the equation of the tangent line.
In both cases, the equations of the tangent lines will be in the form y = mx + b, where m is the slope and b is the y-intercept.
Learn more about line tangent: brainly.com/question/30162650
#SPJ11
4. Elianni has a bucket with a 5-gallon capacity. Elianni puts 12 pints of soapy water in the bucket to wash her blue Hondi. How many gallons of soapy water are in Elianni's bucket? Show your work.
4.part 2 How many more quarts of soapy water will the bucket hold? Show your work.
(middle school)

Answers
1) The number of gallons of soapy water that are in Elianni's bucket are; 1.5 gallons
2) The number of more quarts that it can hold is; 14 more quarts
How to solve Algebra Word Problems?Elianni puts 12 pints of soapy water in the bucket to wash her blue Hondi. From conversion factors, we know that;
1 pint = 1/8 gallon
Thus;
12 pints = 12 * (1/8)
12 pints = (12/8) gallons
= 3/2 = 1.5 gallons.
Due to the fact that the bucket is 5 gallon capacity, It can hold:
5 - 1.5 = 3.5 gallons more.
But from conversion factors, we know that;
1 gallon = 4 quarts.
Thus;
3.5 gallons = 3.5 * 4
= 14 quarts more.
Read more about Algebra Word Problems at; https://brainly.com/question/21405634
#SPJ1
Manuel need to say more than $75 for a class trip. he already has $24 and will save an equal amount each week for the next 6 weeks. Which any quality can be used to determine how much money Manuel should save each week?

Answers
Answer:
the answer is D!
Step-by-step explanation:
I took that quiz :)
HELP URGENT PLEASE
What are the values of
A, B, and x?
A
o
A = [?]°
?
B = [ °
=
Х
11
o
x =
B
11
Enter
![HELP URGENT PLEASE What are the values ofA, B, and x?AoA = [?]?B = [ =11ox =B11Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ScJTemjR7zM0xbRt1naeBxEXgVaDYGtW.png)
Answers
Answer:
A = B = 45°
x = 11√2
Step-by-step explanation:
The sides of the right triangle have equal lengths, so this is an isosceles right triangle. Its acute base angles are complementary and have the same measure: A = B = 45°.
You should know from memory that the hypotenuse of an isosceles right triangle is √2 times the side length, so would be x = 11√2. Even if you don't, you can figure it from the Pythagorean theorem:
x² = 11² +11² = 11²·2
x = 11√2 . . . . . take the square root
Explain how a formula can help solve problems.
Answers
Answer:
A formula can help solve problems as it gives the person a step-by-step mini key or guide when needing to actually answer a mathematical or scientific equation or question.
Joshua earns a salary plus a commission for every painting he sells. the equation c= 40p+75, where c is the commission in dollars and p is the number of paintings, represents how much he earns. compare the functions by comparing their y-intercepts and rates of change.
Answers
The given function is
\(c=40p+75\)Where 40 is the rate of change, and 75 is the y-intercept. This means that Joshua's earnings without the commission are $75, and he earns $40 per painting as commission.
Now, let's find the rate of change of the table
\(m=\frac{y_2-y_1}{x_2-x_1}\)Let's replace the points (1, 115) and (2, 150).
\(m=\frac{150-115}{2-1}=\frac{35}{1}=35\)So, the rate of change of the table is 35, which means the commission per painting is $35.
Now, we use the point-slope formula to find the equation
\(\begin{gathered} y-y_1=m(x-x_1) \\ y-115=35(x-1) \\ y=35x-35+115 \\ y=35x+80 \end{gathered}\)As you can observe, the function shown in the table has 80 as the y-intercept, which means that the earnings without commission are $80.
If we compare, we can say that the first function has greater commission but a lowe salary.5 out of 7 questions. PLEASE help me.

Answers
Answer:
5 units is the distance
Step-by-step explanation:
7,2 is point c
7,7 is point d
7 - 7 = 0
7 - 2 = 5
5 is the answer
Write the equation in slope-intercept form.
7x = 3y − 12
A. y=73x+4
B. 3y−7x=12
C. y−11=73(x−3)
D. y=37x+4
Answers
3y = 7x + 12
y = 3/7x + 4
So what do you think?
Step-by-step explanation:
this is my answer you should mind your own business
Solve the following quadratic equation for all values of x in simplest form. 2 ( x+ 8 ) ^2 + 9 =29
Answers
Answer:
x = -8 + sqrt(10) and x = -8 - sqrt(10)
Step-by-step explanation:
The quadratic equation to be solved is:
2(x + 8)² + 9 = 29
First, we need to simplify the left-hand side of the equation by expanding the squared term:
2(x + 8)(x + 8) + 9 = 29
Simplifying further, we get:
2(x² + 16x + 64) + 9 = 29
Distributing the 2, we get:
2x² + 32x + 128 + 9 = 29
Combining like terms, we get:
2x² + 32x + 137 = 29
Subtracting 29 from both sides, we get:
2x² + 32x + 108 = 0
Dividing both sides by 2, we get:
x² + 16x + 54 = 0
We can solve this quadratic equation by factoring or by using the quadratic formula :
The equation presented is a quadratic equation in standard form, ax² + bx + c = 0, where a = 1, b = 16, and c = 54. To solve this equation, we can use the quadratic formula, x = (-b ± sqrt(b² - 4ac)) / 2a. Plugging in the values, we get x = (-16 ± sqrt(16² - 4(1)(54))) / 2(1) = (-16 ± sqrt(16)) / 2 or (-16 ± 2sqrt(10)) / 2. Simplifying, we get x = -8 ± sqrt(10). Therefore, the two solutions to this equation are x = -8 + sqrt(10) and x = -8 - sqrt(10).
PLEASE ANSWER FAST
On 1 September, Leila starts to go swimming every day.
She swims 30 lengths of the swimming pool every day. The swimming pool is 20m long.
Work out the date when Leila has swum a total of 10 km.
Answers
Answer:
22 November
Step-by-step explanation:
First we have to find the total length she swims in 1 day
= 2(length of the swimming pool) x no. of lengths she swims in 1 day
=2x30x20
=120m she covers in 1 day
10km = 10,000m
no of days= total distance/ distance she covers in 1 day
=10000/120
=83.3 days
Can y’all help me in the question I just asked please!
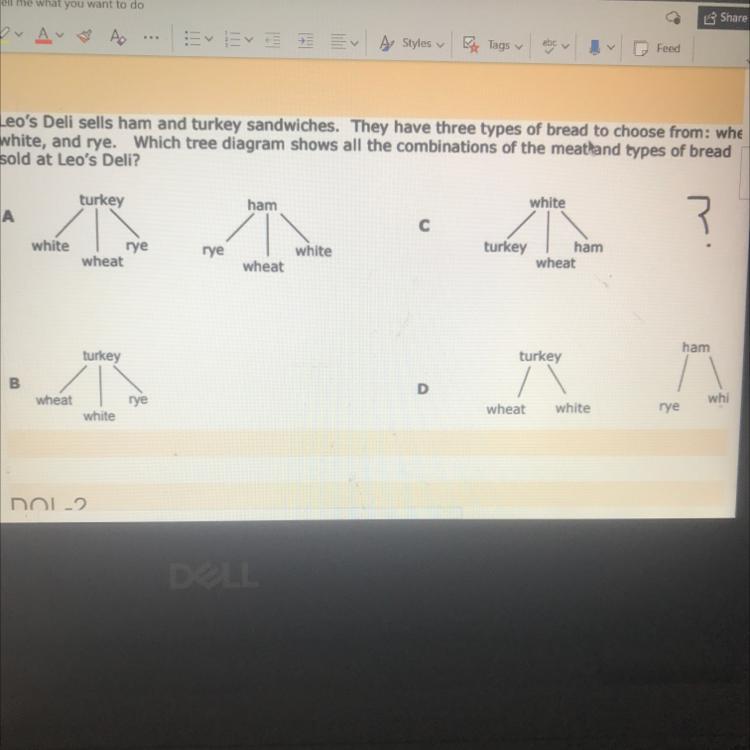
Answers
Answer: A
Step-by-step explanation: A shows a turkey sandwich with all the types of bread and a ham sandwich with all the types of bread.
What is the sum of these decimal numbers?
6.338+2.705+4.099
Answers
Answer:
13.142
Step-by-step explanation:
The sum of the decimal numbers will be 13.142.
What is Decimal number?
A decimal number is a number that consists of a whole and a fractional part.
Given that;
The expression of the decimal numbers are,
⇒ 6.338 + 2.705 + 4.099
Now,
Since, The expression of the decimal numbers are,
⇒ 6.338 + 2.705 + 4.099
Add the numbers as;
6.338
2.705
+4.099
-------------
13.142
Thus, The sum of the decimal numbers will be 13.142.
Learn more about the decimal number visit:
https://brainly.com/question/24342270
#SPJ6
Manuel is packing smaller boxes inside a large box. The
smaller boxes are cube-shaped and measure 6 inches
along each edge. The large box is cube-shaped and
measures 24 inches along each edge. How many
smaller boxes can Manuel fit in the large box?
Answers
The number of the smaller cube-shaped boxes that Manuel can fit into the large cube-shaped box is: 64.
What is the Volume of a Cube?Volume of a cube = a³, where a is the edge length of the cube.
Volume of the smaller cube-shaped boxes = a³ = 6³ = 216 in.³
Volume of the larger cube-shaped box = a³ = 24³ = 13,824 in.³
Number of the smaller boxes that will fit into the large box = 13,824/216 = 64 smaller cube-shaped boxes.
Learn more about volume of a cube on:
https://brainly.com/question/1972490
Patel squeezed oranges so that his family could have fresh-squeezed juice for breakfast. He squeezed StartFraction 4 over 17 EndFraction cups from the first orange, StartFraction 3 over 10 EndFraction cups from the second orange, StartFraction 9 over 20 EndFraction cups from the third orange, StartFraction 3 over 11 EndFraction cups from the fourth orange, and StartFraction 7 over 15 EndFraction cups from the fifth orange. Patel estimates that he needs 2 cups of orange juice for his family. About how much more orange juice does he need to reach his estimate? One-sixth cups Five-sixths cups 1 and two-thirds cups 1 and StartFraction 5 over 6 EndFraction cups
Answers
Answer:
3089/11220
Approximately = 0.2753
Step-by-step explanation:
Patel estimates that he needs 2 cups of Orange juice.
But let's know the amount he already has.
4/17 + 3/10 + 9/20 + 3/11 + 7/15
= 3/10 + 9/20 + 7/15 + 3/11 + 4/17
=( 18 + 27 + 28)/60 + (51+44)/187
= 73/60 + 95/187
=( 13651 + 5700)/11220
= 19351/11220
= 1(8131/11220)
So to complete it two he needs ( 11220-8131)/11220= 3089/11220
Approximately = 0.2753
Answer:
1/6 is your answer.
philip buys a pizza for $5.99 and is given $14.01 as change.
which equation represents the situation if is the amount
philip had before he bought the pizza?
Answers
Answer:
$14.01 + $5.99 = $20
Step-by-step explanation:
Phillip had 20 dollars before he bought the pizza.
CALCULUS ALGREBRA
Mikayla T. asked • 07/09/17
Find the particular solution that satisfies the differential equation and the initial condition.
Find the particular solution that satisfies the differential equation and the initial condition.
1. f '(x) = 8x, f(0) = 7
2. f '(s) = 14s − 12s3, f(3) = 1
Follow2
Add comment
More
Answers
1. The particular solution that satisfies the first differential equation and the initial condition is f(x) = 4x^2 + 7
2. The particular solution that satisfies the second differential equation and the initial condition is f(s) = 7s^2 - 3s^4 + 19
1. To find the particular solution that satisfies the differential equation and the initial condition, we need to integrate the given differential equation and apply the initial condition.
Let's solve each problem step by step:
Given: f'(x) = 8x, f(0) = 7
First, we integrate the differential equation by applying the power rule of integration:
∫f'(x) dx = ∫8x dx
Integrating both sides, we get:
f(x) = 4x^2 + C
To find the value of C, we apply the initial condition f(0) = 7:
f(0) = 4(0)^2 + C
7 = C
Therefore, the particular solution that satisfies the differential equation and the initial condition is:
f(x) = 4x^2 + 7
2. f'(s) = 14s - 12s^3, f(3) = 1
Similarly, we integrate the differential equation:
∫f'(s) ds = ∫(14s - 12s^3) ds
Integrating both sides:
f(s) = 7s^2 - 3s^4 + C
Applying the initial condition f(3) = 1:
f(3) = 7(3)^2 - 3(3)^4 + C
1 = 63 - 81 + C
1 = -18 + C
C = 19
Hence, the particular solution that satisfies the differential equation and the initial condition is:
f(s) = 7s^2 - 3s^4 + 19
Learn more about differential equation at https://brainly.com/question/10622045
#SPJ11
What is equidistant from the three vertices of a triangle?
Answers
Find and classify the critical points of f(x,y)=8r³+ y² + 6xy
Answers
The critical points of the function are (0, 0) and (3/4, -9/4), To classify the critical points, we need to examine the second partial derivatives of f(x, y) at each point
To find the critical points of the function f(x, y) = 8x^3 + y^2 + 6xy, we need to find the values of (x, y) where the partial derivatives with respect to x and y are equal to zero.
Taking the partial derivative with respect to x, we have:
∂f/∂x = 24x^2 + 6y = 0.
Taking the partial derivative with respect to y, we have:
∂f/∂y = 2y + 6x = 0.
Solving these two equations simultaneously, we get:
24x^2 + 6y = 0,
2y + 6x = 0.
From the second equation, we can solve for y in terms of x:
Y = -3x.
Substituting this into the first equation:
24x^2 + 6(-3x) = 0,
24x^2 – 18x = 0,
6x(4x – 3) = 0.
Therefore, we have two possibilities for x:
1. x = 0,
2. 4x – 3 = 0, which gives x = ¾.
Substituting these values back into y = -3x, we get the corresponding y-values:
1. x = 0 ⇒ y = 0,
2. x = ¾ ⇒ y = -9/4.
Hence, the critical points of the function are (0, 0) and (3/4, -9/4).
To classify the critical points, we need to examine the second partial derivatives of f(x, y) at each point. However, since the original function does not provide any information about the second partial derivatives, further analysis is required to classify the critical points.
Learn more about partial derivatives here:
https://brainly.com/question/32387059
#SPJ11
6 out of the 60 employees at the sports shop are part-time employees. What percentage of the employees at the sports shop work part-time?
Answers
Percentage of part time employees = (part-time employees/total employees) * 100 = (6/60) * 100 = 1/10 * 100 = 10%
Convert 100 in. to yards, feet, and inches.
Answers
Answer: 2.78 Yards, 8.33 ft,
Step-by-step explanation:
Answer:
100 in. = 100 inches, 8 feet 4 inches, or 2.77777777778 yards.
Step-by-step explanation:
which two values of x are roots of the polynomial below 4x^2-6x+1

Answers
Step-by-step explanation:
Just apply the quadratic formula \(x=\frac{-b \left \ {{+} \atop {-}} \right. \sqrt{b^{2}-4ac} }{2a}\) Your equation is \(4x^2-6x+1\) Every quadratic equation follows the general form \(ax^2+bx+c\) In this case \(a=4,b=-6,c=1\) Substitute into the quadratic formula:\(x=\frac{-(-6) \left \ {{+} \atop {-}} \right. \sqrt{(-6)^{2}-4(4)(1)} }{2(4)}\\x=\frac{6 \left \ {{+} \atop {-}} \right. \sqrt{36-16} }{8}\\x=\frac{6 \left \ {{+} \atop {-}} \right. \sqrt{20} }{8}\) Now take note that the square root of any number gives a (+) and (-) result, so two different answers\(x=\frac{6 + \sqrt{20} }{8} ,and\\x=\frac{6 - \sqrt{20} }{8}\) are the answersQuestion is: Solve 3y-6=39
Answers
Answer:
y=15
Step-by-step explanation:
first, add 6 to each side. the equation is now 3y=45
simply divide 45 by 3 to get
y=15
Answer:
y=15
Step-by-step explanation:
3y-6=39
add six to the other side
3y=45
divide 45 by 3
y=15
I don’t understand can someone help me please?

Answers
Answer:
b
Step-by-step explanation:
add all of his assets together
his assets are the numbers listed in the right side of the chart.
4,091 + 25,800 + 3,940 + 2,143 + 9,400 + 21,500 + 34,805
= 101,679
the answer is b
good luck!
help this is dew soon!

Answers
Answer:
Step-by-step explanation:
so 1in is 2.5ft.
6.4 times 2.5 is 16.
4.8 times 2.5 is 12.
16+16+12+12
is 24+32.
which is 56.
answer: B
You buy the following from Best Buy:
1 new Chromebook for $550, 1 wireless mouse for $20, 1 wireless keyboard for $20
What is the Subtotal: $
You use your Elite Members Best Buy credit card to save 6%, how much do you save: $
What is the new Subtotal: $
Sales tax is 5%: $
What is the total: $
t
Answers
Answer:
You buy the following from Best Buy:
1 new Chromebook for $550, 1 wireless mouse for $20, 1 wireless keyboard for $20
What is the Subtotal:
$550 + $20 + $20 = $590$590You use your Elite Members Best Buy credit card to save 6%, how much do you save:
$590 * 0.06 = $35.4$35.4What is the new Subtotal: $
$590 - $35.4 = $554.6$554.6Sales tax is 5%: $
$554.6 * 0.05 = $27.73$27.73What is the total: $
$554.6 + $27.73 = $582.33$582.33Step-by-step explanation:
heart and star pls <3 brainliest will be appreciated <3(っ◔◡◔)っ -{ elyna s }-Rajan is given half a chocolate to divide amongst 4 people including himself what fraction of the whole chocolate is he left with?
Answers
Answer: If Rajan has \(\frac{1}{2}\) of a chocolate bar, then he has to divide it 4.
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\)
Step-by-step explanation:
\(\frac{1}{2}\) ÷ 4
\(\frac{1}{2}\) × \(\frac{1}{4}\)
Multiply the numerators and denominators and you will get: \(\frac{1}{8}\)
Hope this helped!
Consider two vectors A :( 50.0 m, 30 0 East of North) and B: (20.0 m, 40 0 North of West)
Represent both vectors in an x-y coordinate system and find the components of vectors A and B.
Express vector C = 5A - (2/3) B as a linear combination of the unit vectors.
Calculate the magnitude and direction of vector C
Answers
The x-component of vector A: 25 m. The y-component of vector A: 43.3 m. The x-component of vector B: -9.9 m. The y-component of vector B: 15.5 m.Vector C: (131.6 i + 206.2 j)Magnitude of vector C: 243.1 m. Direction of vector C: 57.3° north of the east.
Given information: Vector A:(50.0m, 30°
East of North)Vector B:(20.0m, 40° North of West)
Vector C = 5A - (2/3)B
Represent both vectors in an x-y coordinate system and find the components of vectors A and B: The angle between vector A and the positive x-axis: (90 - 30) = 60 degrees.
The magnitude of vector A: 50.0 m.
The x-component of vector A: Acosθ = 50cos60° = 25 m.
The y-component of vector A: Asinθ = 50sin60° = 43.3 m.
The angle between vector B and the positive x-axis: (90 + 40) = 130 degrees.
The magnitude of vector B: 20.0 m.The x-component of vector B: Bcosθ = 20cos130° = -9.9 m.
The y-component of vector B: Bsinθ = 20sin130° = 15.5 m.
Express vector C = 5A - (2/3)B as a linear combination of the unit vectors:
Vector C = 5A - (2/3)
B=5(25 i + 43.3 j) - (2/3)(-9.9 i + 15.5 j)= (125 i + 216.5 j) + (6.6 i - 10.3 j)= 131.6 i + 206.2
jMagnitude of vector C:|C|=√((131.6)² + (206.2)²)= 243.1 m
Direction of vector C:θ= tan⁻¹((206.2)/(131.6))= 57.3° north of the east.
Therefore, The x-component of vector A: 25 m.
The y-component of vector A: 43.3 m. The x-component of vector B: -9.9 m.
The y-component of vector B: 15.5 m.
Vector C: (131.6 i + 206.2 j)
Magnitude of vector C: 243.1 m. Direction of vector C: 57.3° north of the east.
Learn more about Vector
brainly.com/question/30958460
#SPJ11
If X
=85,σ=7, and n=64, construct a 99% confidence interval estimate of the population mean, μ. ≤μ≤ (Round to two decimal places as needed.)
Answers
The 99% confidence interval estimate of the population mean, μ, is (83.59, 86.41).
To construct a confidence interval estimate of the population mean, we can use the formula:
CI = X ± Z * (σ / √n)
Where:
CI represents the confidence interval,
X is the sample mean,
Z is the critical value corresponding to the desired confidence level,
σ is the population standard deviation, and
n is the sample size.
In this case, X = 85, σ = 7, n = 64, and we want a 99% confidence interval. The critical value, Z, can be found using a standard normal distribution table or calculator. For a 99% confidence level, Z is approximately 2.576.
Substituting the values into the formula, we get:
CI = 85 ± 2.576 * (7 / √64)
Calculating the expression inside the parentheses, we have:
CI = 85 ± 2.576 * (7 / 8)
Simplifying further, we get:
CI = 85 ± 2.576 * 0.875
Finally, calculating the upper and lower limits of the confidence interval, we have:
Lower limit = 85 - (2.576 * 0.875) ≈ 83.59
Upper limit = 85 + (2.576 * 0.875) ≈ 86.41
Therefore, the 99% confidence interval estimate of the population mean, μ, is approximately (83.59, 86.41).
Learn more about mean here:
https://brainly.com/question/31098693
#SPJ11