Given the triangle below with centroid G, determine the following values.
If EG=3.5, then GB= and BE= If AD=15, then AG= and DG= If CG=6x, then FG- and CF=

Answers
Answer:
GB = 7
BE = 10.5
AG = 10
DG = 5
FG = 3·x
CF = 9·x
Step-by-step explanation:
The given parameters are;
The centroid of the ΔABC = G
Segments CF, BE, and AD are median lines
EG = 3.5 Given
∴ EG = 1/3 × BE by definition of the properties of median line
∴ BE = 3 × EG = 3 × 3.5 = 10.5
BE = 10.5
GB = 2/3 × BE = 2/3 × 10.5 = 7 by definition of the properties of median line BE
GB = 7
Similarly;
Given that AD = 15, AG = 2/3 × AD = 2/3 × 15 = 10 by definition of the properties of median line AD
AD = 10
DG = 1/3 × AD = 1/3 × 15 = 5 by definition of the properties of median line AD
DG = 5
Similarly;
Given CG = 6·x
FG = 1/3 × CF
CF = 3 × FG
CG = 2/3 × CF = 2/3 × 3 × FG
∴ CG = 2 × FG
FG = CG/2 = 6·x/
2 = 3·x
FG = 3·x
CF = 3 × FG = CF = 3 × 3 × x = 9·x
CF = 9·x
Related Questions
A random sample of 121 checking accounts at a bank showed an average daily balance of $265. The standard deviation of the population is known to be $77. (a) Is it necessary to know anything about the shape of the distribution of the account balances in order to make an interval estimate of the mean of all the account balances? Explain O No, the mean is larger than the standard deviation so we do not need to know anything about the shape of the distribution O Yes, the sample is large and the standard deviation of the population is known so we also need to know that the shape of the distribution is at least approximately beil shaped O No, the sample is large and the standard deviation of the population is known so we do not need to know anything about the shape of the distribution. O No, the standard deviation is larger than the mean so we do not need to know anything about the shape of the distribution. Yes, the mean is larger than the standard deviation so we also need to know that the shape of the distribution is at least approximately bell shaped (b) Find the standard error of the mean (in dollars). (c) Give a point estimate of the population mean (in dollars). (d) Construct an 80% confidence interval for the population mean (in dollars). (Round your answers to the nearest cent.) $ to $. (e) Construct a 95% confidence interval for the population mean (in dollars), (Round your answers to the nearest cent) $ to $
Answers
(a) No, sample is large and the standard deviation of the population is known so we do not need to know anything about the shape of the distribution. Therefore, the correct option is C.
(b) The standard error of the mean is $7.
(c) The point estimate of the population mean is $265.
(d) The 80% confidence interval for the population mean is $254.62 to $275.38.
(e) The 95% confidence interval for the population mean is $249.94 to $280.06.
a) The correct answer to whether it is necessary to know anything about the shape of the distribution of the account balances in order to make an interval estimate of the mean of all the account balances is: No, the sample is large and the standard deviation of the population is known, so we do not need to know anything about the shape of the distribution. With a large sample size, the Central Limit Theorem allows us to assume that the sampling distribution of the mean will be approximately normal. Hence, the correct answer is option C.
(b) The formula for standard error of the mean is:
SE = σ/√n
where σ is the population standard deviation, n is the sample size, and √ is the square root. Substituting the given values, we get:
SE = 77/√121
SE = 7
(c) The point estimate of the population mean is simply the sample mean, which is given as $265.
(d) To construct an 80% confidence interval, we need to use the formula:
CI = x ± zα/2 * (σ/√n)
where x is the sample mean, zα/2 is the z-score corresponding to the desired level of confidence (in this case, 80% or 0.80), σ is the population standard deviation, and n is the sample size. From the z-table, we find that the z-score for an 80% confidence interval is 1.28. Substituting the given values, we get:
CI = $265 ± 1.28 * (77/√121)
CI = $265 ± $10.38
CI = $254.62 to $275.38
(e) To construct a 95% confidence interval, we follow the same formula but use a z-score of 1.96 (from the z-table) for the desired level of confidence. Substituting the given values, we get:
CI = $265 ± 1.96 * (77/√121)
CI = $265 ± $15.06
CI = $249.94 to $280.06
Learn more about Standard error:
https://brainly.com/question/29037921
#SPJ11
The daytime high temperature on the moon can reach 130°C. The nighttime low temperature can get as low as −110°C. What is the difference between the high and low temperatures?
Answers
Answer:
240
Step-by-step explanation:
remember that to get from positive to negative you have to go from positive to 0 then to negative .
however the easiest way of solving this is
add both the values , ignore the sign
130 + 110
the difference in the temperature is :
= 240 degrees
What is the HCF of 36,60,84?
Answers
Jasmine took her little sister Julia out for her birthday. They went to a nice dinner where Jasmine paid for the meal. Her meal cost $12.33 and Julia's cost $17.88. There was a tax of 7% and she tipped 20%. They then went to a concert where Jasmine paid again, and each ticket was $25. They got 2 tickets. Jasmine started the evening with $100. How much does she have after their fun evening?
Jasmine has left.
Answers
Jasmine has $11.17 left after their fun evening.
What is the arithmetic operations?
Arithmetic operations involve basic mathematical operations such as addition, subtraction, multiplication, and division.
Let's start by calculating the total cost of dinner.
Jasmine's meal cost $12.33 and Julia's cost $17.88, so the total cost of the meal before tax and tip was:
$12.33 + $17.88 = $30.21
Adding the 7% tax gives:
$30.21 + 0.07($30.21) = $32.36
Adding the 20% tip gives:
$32.36 + 0.2($32.36) = $38.83
So the total cost of dinner was $38.83.
Next, let's calculate the cost of the concert. They bought 2 tickets at $25 each, so the total cost of the concert was:
2($25) = $50
Adding the cost of dinner and the concert gives:
$38.83 + $50 = $88.83
Jasmine started with $100, so after paying for dinner and the concert, she has:
$100 - $88.83 = $11.17
Hence, Jasmine has $11.17 left after their fun evening.
To learn more about arithmetic operations, Visit
https://brainly.com/question/20628271
#SPJ1
-2x + 6 = 16
show work
Answers
Answer:
x=-5
Step-by-step explanation:
-2x+6=16
-2x=10
x=-5
Which one of the following statements expresses a true proportion?
O A. 7:9 = 8:9
OB. 3:4 = 9:12
O C.54:9 = 6:3
OD. 2:1 1:2
Answers
Answer:
The answer is B.
Step-by-step explanation:
A true proportion is a set of ratios that equal each other.
For example, 1:2=2:4 is a proportion.
As we look through the list, we observe only B equals each other. Imagine 3:4 and 9:12 as a fraction. (¾ and 9/12). If we reduce 9/12, we get ¾. Thus, 3:4 = 9:12:)
I hope this helps!
what are the answers to this?? please help!!!

Answers
its a and c maybe. cuz im smart
Reason
a = 35 + 210s + 325t ❌
b = 35 + 30s - 45t ✅
c= 35 + 30s -45t ✅
d= 35 + 30s -45 ❌
e = -35 + 30s - 45t ❌
pls help im stuck in this question

Answers
Based on the number of members and the ratio in which they chose the types of film, the number who chose Action in the second week more than the first week is 6 people.
How many chose Action more in the second week?Assuming that the number of members is 99 members, the number who chose Action on the second week were:
= (7 / (5 + 7 + 6)) x 99
= 39 people
The number who chose Action in the first week:
= (5 / (2 + 5 + 8)) x 99
= 33
The difference is:
= 39 - 33
= 6 people
Find out more on ratios at https://brainly.com/question/12024093
#SPJ1
Type the correct answer in the box. Consider the table below. x y -1 -5 0 5 1 11 2 13 3 11 Complete the standard form equation representing the quadratic relationship displayed above, where a, b, and c are constants.
Answers
Here, a = -2 and b = 8. So the standard form equation of the quadratic relationship displayed in the table is:y = -2x² + 8x + 5.
What is standard form equation?The mathematical representation of an equation with integer coefficients for each variable and a predetermined sequence of variables is known as a standard form equation.
For instance, Ax + By = C is the conventional form of a linear equation.
To find the standard form equation of the quadratic relationship displayed in the table, we can use the general form of a quadratic equation:
y = ax² + bx + c
Using the points (-1, -5), (0, 5), and (1, 11), we get the following system of equations:
a(-1)² + b(-1) + c = -5
a(0)² + b(0) + c = 5
a(1)² + b(1) + c = 11
Simplifying each equation and rearranging terms, we get:
a - b + c = -5
c = 5
a + b + c = 11
Substituting c = 5 into the first and third equations, we get:
a - b = -10
a + b = 6
Adding these two equations, we get:
2a = -4
Therefore, a = -2. Substituting this value into either of the equations a - b = -10 or a + b = 6, we can solve for b:
-2 - b = -10
b = 8
To know more about quadratic equation visit:
https://brainly.com/question/30098550
#SPJ1
HELPPP PLEASEEEEEE!!!!!!!!!1

Answers
Hi!
We can see the river is a straight line.
This means that the angles that fall upon it are supplementary angles, and will add up to 180 degrees.
Therefore:
\(x+2x+21=180\)
Combine like terms:
\(3x+21=180\)
Subtract 21 from both sides:
\(3x=159\)
Divide both sides by 3:
\(x=53\)
Therefore, the value of x is 53 degrees.
PLEASE HELP!!! I WILL RATE YOU BRAINLIEST
The first laptop ever was sold was the Osborne 1. It came onto the market in 1981, and it had a mass of 11 kg. Suppose that since 1981 the mass of laptops has decreased at an average rate of 4.7% per year. What was the approximate weight of a laptop in 2019?
a. 6.43 kg
b. 8.10 kg
c. 4.62 kg
d. 1.76 kg
Answers
Answer: (d)- 1.76 kg
Step-by-step explanation:
Given
The first laptop mass was 11 kg
The rate of mass decreases by 4.7% per year
In 1982, it was
\(\Rightarrow 11-11\times 4.7\%=11-11\times 0.047\\\Rightarrow 11(1-0.047)\ kg\)
In 1983, it was
\(\Rightarrow 11(1-0.047)-11(1-0.047)\times 0.047=11(1-0.047)^2\)
In 2019 i.e. after 38 years, it is
\(\Rightarrow 11(1-0.047)^38=11\times 0.953^{38}=1.76\ kg\)
Ten prizes are given to a class with 100 students. Each student can receive at most one prize. Alice and Bob are two students in the class. If the prizes are identical, how many ways are there to distribute the prizes so that either Alice or Bob (or both) receive a prize?
Answers
There are 7,941,658,620 different ways to divide up the prizes so that either Alice or Bob, or both, win.
To count the number of ways to distribute the prizes such that Alice and/or Bob receive a prize, we will use the principle of inclusion-exclusion.
Let A be the event that Alice receives a prize and B be the event that Bob receives a prize. Then, we want to count the number of outcomes in the event A∪B (that is, the number of ways in which either Alice or Bob or both receive a prize).
By the principle of inclusion-exclusion, we have:
|A∪B| = |A| + |B| - |A∩B|
where |A| is the number of outcomes in event A, |B| is the number of outcomes in event B, and |A∩B| is the number of outcomes in the intersection of events A and B.
To count these values, we consider the following cases:
Case 1: Alice and Bob both receive a prize.
In this case, we have 8 prizes left to distribute to the remaining 98 students. The number of ways to distribute these prizes is:
98\(c_{8}\)
Case 2: Alice receives a prize but Bob does not.
In this case, we have 1 prize that must be given to Alice, and 9 prizes left to distribute to the remaining 98 students. The number of ways to distribute these prizes is:
98\(C_{9}\)
Case 3: Bob receives a prize but Alice does not.
This is the same as Case 2, so the number of ways is also 98\(C_{9}\)
Adding up the number of outcomes from each case gives us:
|A∪B| = 98\(c_{8}\) + 2{98\(C_{9}\)}
Plugging in the values, we get:
|A∪B| = 7,941,658,620
Therefore, there are 7,941,658,620 ways to distribute the prizes such that either Alice or Bob or both receive a prize.
To learn more about principle of inclusion-exclusion:
https://brainly.com/question/27975057
#SPJ4
what is the lateral surface area of a rectangular pyramid with a base of 12,16 and a height of 6,8
Answers
Answer:
It's 8
Step-by-step explanation:
4x+8y=-24 what is this how do i do it
Answers
Answer:
if you're rewriting the equation the answer is x+2y+6=0 explanation : I moved the constant to the left handside and changed its sign, then divided both sides of the equation by 4. If youre solving for x the answer is x=-6-2y . If youre solving for y its y=-3- x/2 ( fraction)
Step-by-step explanation:
Define the term functions limits and continuity as used in
business calculus and use an example
Answers
In business calculus, the term "functions" refers to mathematical relationships that associate inputs (typically denoted as x) with corresponding outputs (typically denoted as y). Functions can represent various aspects of business operations, such as revenue, cost, profit, demand, and supply.
The concept of "limits" in calculus deals with the behavior of a function as the input approaches a particular value. It determines the value that the function approaches or tends to as the input gets arbitrarily close to a specified value. Limits are essential for analyzing the behavior of functions near certain points, understanding rates of change, and evaluating derivatives and integrals.
"Continuity" of a function refers to its smooth and unbroken nature, without any abrupt jumps, holes, or vertical asymptotes. A function is continuous if its graph can be drawn without lifting the pen from the paper. Continuity ensures that small changes in the input correspond to small changes in the output, which is crucial for reliable analysis and prediction.
For example, consider the function f(x) = 2x + 1. This linear function represents a business scenario where x represents the number of units sold, and f(x) represents the total revenue generated. The limit of f(x) as x approaches 2 is 5, indicating that as the number of units sold approaches 2, the total revenue approaches $5. Since f(x) = 2x + 1 is a linear function, it is continuous across its entire domain.
Learn more about functions, limits, and continuity in calculus here:
brainly.com/question/29297331
#SPJ11
Which values represent the independent variable? (–2, 4), (3, –2), (1, 0), (5, 5) A. {–2, 3, 1, 5} B. {4, –2, 0, 5} C. {–2, 4, 3, –2} D. {–2, –1, 0, 5} Please select the best answer from the choices provided A B C D
Answers
Answer:
The independent variable is the variable that is manipulated or changed during an experiment. In this case, the independent variable is represented by the x-values of the given points.
So, the answer would be option A: {-2, 3, 1, 5}
Step-by-step explanation:
brainliest Plsssss
please answer the question i need help
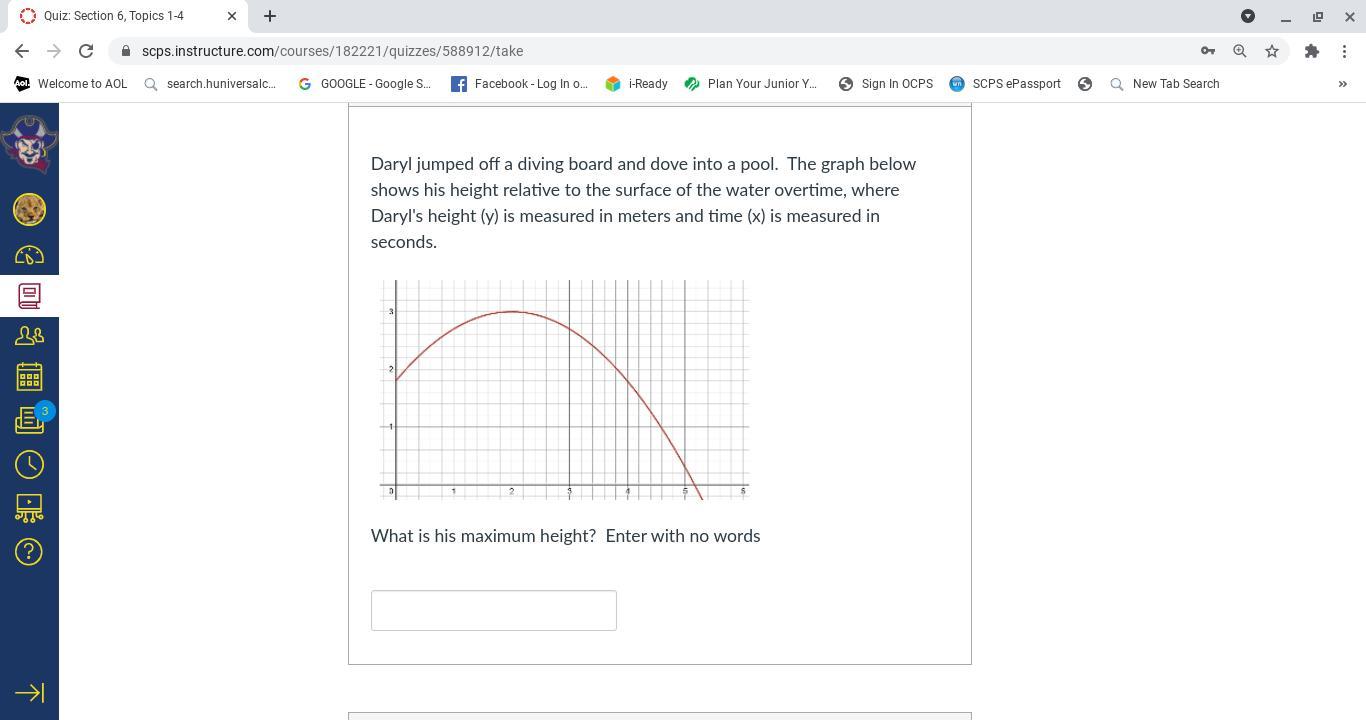
Answers
Answer:
3
Step-by-step explanation:
since the highest value of curve is at 3 m
2 Two burgers and three fries have 1740 calories. A burger has 170 more calories than a fry. How many
calories are in each?
Answers
Answer:
Burger Calories Individual: 450
Fry Calories Indicidual: 280
Step-by-step explanation:
First, since there are 2 burgers and each burger has 170 more calories, we will subtract 170 + 170.
170 + 170 = 340.
1740 - 340 = 1400 ( this makes it good for the next part )
Since we have 2 burgers and 3 fries, that will be 5 in total.
All we will have to do is divide 1400 by 5 to get our answer.
1400 ÷ 5 = 280.
Now we know that each of the fries had 280 calories.
280 + 170 = 450 ( add 170 because the instructions say the burger had 170 calories more. )
Therefore, the burgers each had 450 calories and the fries each had 280.
-kiniwih426
Create a rational fiction with vertical asymptotes at x=-6 and x=-1, a HOLE at x=-9 and an x-intercept at x=0

Answers
We need to know about asymptotes and holes to solve this problem. The radical function is \(\frac{x^{2} +9x}{x^{3}+16 x^{2} +69x+54}\)
A vertical asymptote is a vertical line that guides the graph of a function but is not a part of it. If there is a same factor in the numerator and the denominator then it is called a hole. A horizontal asymptote is a horizontal line with which the graph of the function seems to coincide but does not really coincide. In this question we know that vertical asymptotes are at x=-6 and x=-1, so we know that these are the factors of the denominator. A hole lies at x=-9, so this is a common factor for numerator and the denominator. There is an x-intercept at x=0 which means we have a this factor in the numerator.
f(x)=\(\frac{x(x+9)}{(x+9)(x+6)(x+1)}\)=\(\frac{x^{2}+9x }{(x+9)(x^{2} +7x+6)} =\frac{x^{2} +9x}{x^{3}+16 x^{2} +69x+54}\)
Therefore the radical function is \(\frac{x^{2} +9x}{x^{3}+16 x^{2} +69x+54}\)
Learn more about asymptotes here:
https://brainly.com/question/2937678
#SPJ1
Two points are shown on the line in the graph below

Answers
Answer:
y=1/2x+1
Step-by-step explanation:
Its simple, trust me
Pattern A: start with 12 and add 12 Pattern B: start with 4 and add 2 Which statement best describes the relationship between the corresponding terms of Patter A and Pattern B
Answers
Answer:
Each term in Pattern A is equals to 6 times the value of corresponding term in Pattern B and subtract 12
Step-by-step explanation:
Given - Pattern A: start with 12 and add 12
Pattern B: start with 4 and add 2
To find - Which statement best describes the relationship between the
corresponding terms of Patter A and Pattern B.
Proof -
To find the relationship between the Pattern a and pattern B , firstly we have to find few terms of both the Patterns , so that we can see how the digits of both the Patterns are realted
Now,
For Pattern A :
1st digit = 12
2nd digit = 12 + 12 = 24
3rd digit = 24 + 12 = 36
4th term = 36 + 12 = 48
5th term = 48 + 12 = 60
.
.
.
and so on
Now,
For Pattern B :
1st digit = 4
2nd digit = 4 + 2 = 6
3rd digit = 6 + 2 = 8
4th term = 8 + 2 = 10
5th term = 10 + 2 = 12
∴ we get
Terms of Pattern A : 12, 24, 36, 48, 60, ....
Terms of Pattern B : 4, 6, 8, 10, 12, ....
As we can see that
4×6 - 12 = 12
6×6 - 12 = 24
8×6 - 12 = 36
10×6 - 12 = 48
12×6 - 12 = 60
.
.
The pattern is - Multiply by 6 in Pattern B and after that subtract by 12 , we get Pattern A.
Term in Pattern A = 6×corresponding term of Pattern B - 12
i.e. , we get
Each term in Pattern A is equals to 6 times the value of corresponding term in Pattern B and subtract 12
when joe bowls, he can get a strike (knock down all of the pins) 60 percent of the time. how many times more likely is it for joe to bowl at least three strikes out of four times as it is for him to bowl zero strikes out of four tries? round answer to the nearest whole number.
Answers
Joe is about 10 times more likely to bowl at least three strikes out of four tries than to bowl zero strikes out of four tries.
To find the probability of Joe bowling at least three strikes out of four tries, we need to consider the different combinations of strikes and non-strikes he can get.
There are four possible outcomes:
- strike, strike, strike, non-strike
- strike, strike, non-strike, strike
- strike, non-strike, strike, strike
- non-strike, strike, strike, strike
The probability of getting a strike is 0.6, and the probability of not getting a strike (a non-strike) is 0.4. So for each outcome, we can calculate the probability as follows:
- Probability of strike, strike, strike, non-strike = 0.6 x 0.6 x 0.6 x 0.4 = 0.0864
- Probability of strike, strike, non-strike, strike = 0.6 x 0.6 x 0.4 x 0.6 = 0.0864
- Probability of strike, non-strike, strike, strike = 0.6 x 0.4 x 0.6 x 0.6 = 0.0864
- Probability of non-strike, strike, strike, strike = 0.4 x 0.6 x 0.6 x 0.6 = 0.0864
To find the probability of Joe bowling at least three strikes, we need to add up the probabilities of the last three outcomes, since they all have at least three strikes:
0.0864 + 0.0864 + 0.0864 = 0.2592
So the probability of Joe bowling at least three strikes out of four tries is 0.2592, or about 26% (rounded to the nearest whole number).
To find the probability of Joe bowling zero strikes, we can use the same approach:
- Probability of non-strike, non-strike, non-strike, non-strike = 0.4 x 0.4 x 0.4 x 0.4 = 0.0256
So the probability of Joe bowling zero strikes out of four tries is 0.0256, or about 3% (rounded to the nearest whole number).
To find how many times more likely it is for Joe to bowl at least three strikes than to bowl zero strikes, we can divide the probability of the first outcome by the probability of the second outcome:
0.2592 / 0.0256 = 10.125
Know more about probability here:
https://brainly.com/question/30034780
#SPJ11
suppose that the probability of event a is 0.4 and the probability of event b is 0.5. what is p( a b) if a and b are mutually exclusive? what i
Answers
If events A and B are mutually exclusive with probabilities P(A) = 0.4 and P(B) = 0.5, respectively, then the probability of their intersection, P(A ∩ B), is equal to zero.
If events A and B are mutually exclusive, it means that they cannot occur simultaneously. In other words, if event A happens, event B cannot happen, and vice versa. Mathematically, this can be represented as:
P(A ∩ B) = 0
The probability of the intersection of mutually exclusive events is always zero because there is no overlap between the events.
In the given scenario, the probability of event A is 0.4 (P(A) = 0.4) and the probability of event B is 0.5 (P(B) = 0.5). Since events A and B are mutually exclusive, we know that P(A ∩ B) = 0.
Therefore, the probability of the intersection of events A and B, denoted as P(A ∩ B), is equal to zero.
This result makes sense intuitively because if two events are mutually exclusive, they cannot occur at the same time. So the probability of both events happening together is zero.
For more such questions on mutually exclusive visit:
https://brainly.com/question/30644106
#SPJ11
Construct AKUM, if KL = 8cm, LM =
10cm and KM = 6cm. Measure the
largest angle in the triangle.
Answers
AKUM is an isosceles triangle. The sides are 8cm, 10cm and 6cm, and the angles are 42°, 42° and 96°. The largest angle in the triangle is 96°.
1. AKUM is an isosceles triangle, which means that two of its sides are equal.
2. The sides given are KL = 8cm, LM = 10cm and KM = 6cm.
3. Using the Law of Cosines, we can find the measure of the angles in the triangle:
a. Angle K = arccos((KL^2 + LM^2 - KM^2) / (2*KL*LM)) = 42°
b. Angle L = arccos((KL^2 + KM^2 - LM^2) / (2*KL*KM)) = 42°
c. Angle M = arccos((LM^2 + KM^2 - KL^2) / (2*LM*KM)) = 96°
4. Therefore, the largest angle in the triangle is 96°.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
use mental math to determine the best estimate for √65

Answers
Answer:
8
Step-by-step explanation:
\(65 \approx 64 \implies \sqrt{65} \approx 8\)
A(n)=2+(n-1)(3) find the fourth and tenth term of the sequence
Answers
Answer:
The fourth term is 11 and the tenth term is 29
Step-by-step explanation:
Let us use the given formula to solve the question
∵ A(n) = 2 + (n - 1)(3) is the formula of the nth term of an sequence
∵ n is the position of the term in the sequence
∴ For the fourth term n = 4
∴ For the tenth term n = 10
→ Substitute n by 4 in the formula above to find the fourth term
∵ A(4) = 2 + (4 - 1)(3)
∴ A(4) = 2 + (3)(3)
∴ A(4) = 2 + 9
∴ A(4) = 11
∴ The fourth term is 11
→ For the tenth term put n = 10
∵ n = 10
∵ A(10) = 2 + (10 - 1)(3)
∴ A(10) = 2 + (9)(3)
∴ A(10) = 2 + 27
∴ A(10) = 29
∴ The tenth term is 29
write the sequence of natural numbers which leaves the remainder 3 on didvidng by 10
Answers
The sequence of natural numbers that leaves a remainder of 3 when divided by 10 is:
3, 13, 23, 33, 43, 53, 63, 73, 83, 93, 103, 113, ...
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Question 6 of 30
On a unit circle, 0 = 60°. Identify the terminal point and tan 8.
O A. Terminal point: (,); tan 0 = √3
OB. Terminal point: (3,1); tan 0 = 3
OC. Terminal point: (,); tan 0 = √3
O D. Terminal point: (1,3); tan 0 =
SUBMIT

Answers
On a unit circle, 0 = 60°, hence the terminal point is (,); tan 0 = √3. It rotates symmetrically around the center at all angles.
what is circle ?In the plane, a circle is created by each point that is a specific distance from another point (center). Therefore, it is a curve made up of points that are spaced out from one another in the plane in a fixed manner. It rotates symmetrically around the center at all angles. Every pair of points in the plane of a circle, which is a closed two-dimensional object, are evenly distanced from the "center." Specular symmetry is produced by a line that traverses the circle. It rotates symmetrically around the center at all angles.
given
θ = 30 °
terminal point = cos 30° , sin30°
= (underroot 2 , 1/2 )
tan30° = 1/ underroot 3 = underroot3/3
On a unit circle, 0 = 60°, hence the terminal point is (,); tan 0 = √3. It rotates symmetrically around the center at all angles.
To know more about circle visit:
https://brainly.com/question/29142813
#SPJ1
Can someone please help me with this?

Answers
The value of the angle m<CED is 100 degrees
What are corresponding angles?Corresponding angles are simply described as those angles that are formed by same corners or corresponding corners with a transversal when two parallel lines are joined by any other line.
Also, corresponding angles are created when two parallel lines are intersected by a transversal.
The different types of corresponding angles are;
Those angles formed by parallel lines and transversals.Those angles formed by non-parallel lines and transversals.Note that corresponding angles are equal.
From the information given, we have that;
m < BHG = m<CED
If m< BHG = 100 degrees
Then, m< CED = 100 degrees
Learn about corresponding angles at: https://brainly.com/question/28769265
#SPJ1
classify the quadric surface. 16x2 − y2 + 16z2 = 4
Answers
The given equation, 16x² - y² + 16z² = 4, represents a quadric surface known as an elliptic paraboloid.
To determine the classification, we can examine the coefficients of the squared terms. In this case, the coefficients of x², y², and z² are positive, indicating that the surface is bowl-shaped. Additionally, the signs of the coefficients are the same for x² and z², indicating that the bowl opens upward along the x and z directions.
The negative coefficient of y², on the other hand, means that the surface opens downward along the y direction. This creates a cross-section in the shape of an elliptical parabola.
Considering these characteristics, the given equation represents an elliptic paraboloid.
Learn more about quadric surface at https://brainly.com/question/30256242
#SPJ11