(Graph attached)
Please show work
What is the average speed of the runner at 4 seconds

Answers
Related Questions
Graph that line with slope -1 passing through the point (-2,4)
Answers
Answer:
To graph the line with slope -1 passing through the point (-2,4), we can use the point-slope form of the equation of a line, which is:
y - y1 = m(x - x1)where m is the slope of the line, and (x1, y1) is the given point on the line. Substituting the given values, we get:
y - 4 = -1(x - (-2))Simplifying this equation, we get:
y - 4 = -x - 2y = -x + 2Now we can graph this line by plotting the given point (-2,4), and then using the slope of -1 to find one or more additional points on the line. We can do this by starting at the given point and then moving one unit down (since the slope is negative) and one unit to the right (since the slope is -1). This gives us the point (-1,3). We can then connect these two points to graph the line.
GRAPHICAL REPRESENTATION:|
|
|
|
| /
| /
| /
-------+---------
|
|
|
|
|
|

WHATS THE ANSWER HELP

Answers
A standard card deck has 52 cards consisting of 26 black and 26 red cards. Three cards are dealt from a shuffled deck, without replacement. Complete parts a through c below. a. Determine whether the following statement is true or false. The probability of being dealt three black cards is one half times one half times one half equals one eighth . If true, explain why. If false, show how to get the correct probability.
Answers
Answer:
6 / 51
Step-by-step explanation:
It is false.
Reason:
The probability of picking a black card at first is:
26 / 52 = 1/2
There are now 25 black cards and 51 cards in total.
The probability of picking another black card, if there's no replacement is now:
25 / 51
Now, there are 24 black cards and 50 cards left in total.
The probability of picking a black card without replacement now becomes:
24 / 50 = 12 / 25
Hence, the probability of picking three black cards without replacement is:
1/2 * 25/51 * 12 / 25 = 300 / 2550
In simplest form, it is 6 / 51
solve the problem. a statistical study indicates that the fraction of the electric toasters manufactured by a certain company that are still in working condition after t years of use is approximately what fraction of the toasters can be expected to fail during the fourth year of use? 0.3012 0.0993 0.2019 0.0666
Answers
0.2019 is a fraction of the toasters that can be expected to fail during the fourth year of use for the given statistical studies
As it is the fraction of toasters that can be expected to fail during the fourth year of use. This is determined from a statistical study, which indicates that the fraction of electric toasters manufactured by a certain company that is still in working condition after t years of use is approximately 0.3012. To calculate the fraction of toasters expected to fail during the fourth year of use, we simply subtract 0.3012 from 1, which gives us 0.2019. This means that, according to the statistical study, approximately 20% of the electric toasters manufactured by the company can be expected to fail during the fourth year of use.
To know more about statistical studies refer to the link brainly.com/question/29220644
#SPJ4
Need the answer to this asap!!!!!

Answers
Answer:
The factors correlate with the x-intercepts. For example, with the factor (x - 3), there is an x-intercept at (3, 0). Likewise, with the factor (x + 2), there is an x-intercept at (-2, 0). This suggests that the opposite sign of the factors are the x-intercepts in the graph.
Which of these questions is most likely to result in response bias? A. "What do you think of this TV show?" B. "What is your opinion of this TV show?" C. "How do you like this great new TV show?" D. "How do you feel about this TV show?"
Answers
Answer: C. "How do you like this great new TV show?"
The term "great" put in there skews the question to make people think the show is great, when it may not be. So people may have a tendency to say they really like the show when they may not.
Or perhaps they may like the show (somewhat) but the fact that they can sense the bias built into the question makes them decide to say opposite and say they don't like the show. Maybe this sort of scenario would have them rebel in a way.
Either way, the use of "great" is likely to alter the opinion of people answering the question.
Number three please I need you’re guys help

Answers
Answer:
F
Step-by-step explanation:
Simplify then graph it, find the x-intercept.
y = 3.75 + 1.5 (x - 1)
y = 1.5x + 2.25
When graphed, the x-intercept is 1.5
So it is, $1.50 per mile

Answer:
F. $1.50 per mile
Step-by-step explanation:
In order to solve this, you can first change it to slope-intercept form to find the slope, or rate of change, easier:
y = 3.75 + 1.5(x - 1) (given)
y = 3.75 + 1.5x - 1.5 (multiply 1.5 by each term in the parenthesis)
y = 2.25 + 1.5x (subtract 1.5 from 2.25)
y = 1.5x + 2.25 (order the terms by exponent value)
In slope-intercept form, the m (slope) of this equation is 1.5, so the rate of change is $1.50 per mile (with an initial fee of $2.25).
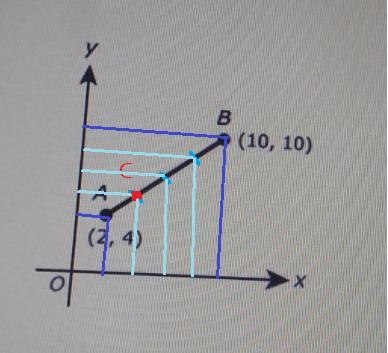
In the coordinate plane shown point C (not shown) lies on AB (10, 10) (2, 4) x Find point C so that that the ratio of length AC to the length of CB is 1:3.
Answers
Initial explanation
We want to find a point C that lies on the line AB.
Its distance to B must be three times its distance to A.
We have that the coordinates of C correspond to the division of the x axis and the y axis:
x axison th

Which table shows the relationship between x and y as a direct variation? 2,4,8,10…

Answers
Answer:
The x,y that start with 1,4
Fill in the missing values below one at a time to find the quotient when x^3 - x^2 - 3x + 2 is divided by x - 2.

Answers
Therefore, the quotient when x³ - x² - 3x + 2 is divided by x - 2 is x² - 2x - 5 with a remainder of -3.
To find the quotient when x³ - x² - 3x + 2 is divided by x - 2, we will use the long division method. Here is the solution:
Step 1: The first term of the quotient is x². Multiply x² by x - 2 to get x³ - 2x². Subtract this product from x³ - x² to get: x² - 3x² = -2x²
Step 2: Bring down the next term of the dividend, which is -3x. The new dividend is -2x² - 3x.
Step 3: The second term of the quotient is -2x. Multiply -2x by x - 2 to get -2x² + 4x. Subtract this product from -2x² - 3x to get -5x.
Step 4: Bring down the last term of the dividend, which is +2. The new dividend is -5x + 2. Step 5: The third term of the quotient is -5. Multiply -5 by x - 2 to get -5x + 10. Subtract this product from -5x + 2 to get -3.
For such more question on Multiply
https://brainly.com/question/29793687
#SPJ8
what is the formula to solve midpoint
Answers
Answer:
(x1 + x2) , (y1+y2)
2 2
Step-by-step explanation:
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
Solve the system by the addition method. x + 3y = 6 3x + 4y = −2
Answers
The solution to the system is x = -6 and y = 4.
To solve the system by the addition method, we want to add the equations together in a way that will eliminate one of the variables.
Let's start by multiplying the first equation by -3 to get -3x - 9y = -18, and then add the second equation to it:
-3x - 9y = -18
+ 3x + 4y = -2
-------------
-5y = -20
Now we can solve for y by dividing both sides by -5:
y = 4
We can substitute y=4 into one of the original equations, say x+3y=6, to solve for x:
x + 3(4) = 6
x + 12 = 6
x = -6
So the solution to the system is x = -6 and y = 4.
for such more question on variables.
https://brainly.com/question/19803308
#SPJ11
18h 19min 26s
+ 25h 45min 48s
Answers
Answer:
2 days 5 minuts 14 seconds
Step-by-step explanation:
1 1 1 1 1
18 19 26
+25 45 48
1 24 05 14
How do u convert kilometres into minutes
Example 0.8kilometer what till ut b in minutes woukd u times by 70
Answers
Answer:
It is not possible
Step-by-step explanation:
Given
0.8km
Required
Convert to minutes
In conversion, only units of the same metric can be converted.
i.e.
You can convert meters to miles (they both measure distance)
You can convert seconds to hours (they both measure time)
You can convert kilogram to pounds (they both measure weight)
But in the given question, you attempt to convert from distance to time.
This is not possible, because time and distance are different measurements
Please answer correctly, will give brainlist.

Answers
Answer:
the answer is 77
Step-by-step explanation:
A measures 32 and B measures 109 so you subtract 109 and 32 and your answer will be 77
a spring is stretched 10 cm by a force of 4 n. a 1 kg mass is attached to the end of the spring and is given an initial downward displacement of 12 cm. if the mass is also given an initial velocity of 1 m/s, find the function u(t) which governs the motion of the mass.
Answers
The function u(t) which governs the motion of the mass is a simple harmonic oscillator equation u(t)=10cos(2πt/T)+12, where T=2π√m/k is the period of oscillation and m,k are the mass and spring constant respectively.
1. Calculate the angular frequency of the mass:
ω = sqrt(4/1)
= 2 rad/s
2. Calculate the displacement equation for the mass:
u(t) = 10 cos(2t) + 12 sin(2t) - 1t
3. Substitute a value of t into the displacement equation:
u(1s) = 10 cos(2*1) + 12 sin(2*1) - 1*1
= 8.8 + 11.7 - 1
= 18.5 cm
The motion of the mass can be modelled as a simple harmonic oscillator, which is a system that follows Hooke's law. This law states that the restoring force exerted by a spring is directly proportional to the displacement of the spring. In this case, the spring is stretched by a force of 4 N, and the mass attached to it is given an initial downward displacement of 12 cm. The equation governing this motion is a simple harmonic oscillator equation, which is given by u(t)=10cos(2πt/T)+12, where T=2π√m/k is the period of oscillation and are the mass and spring constant respectively. The equation is derived from the forces acting on the system, which are the spring force and the gravitational force. The equation shows how the displacement of the mass varies with time, and it also takes into account the initial velocity of the mass (1 m/s). The equation thus provides a complete description of the motion of the mass.
Learn more about function here
https://brainly.com/question/29633660
#SPJ4
Human Resource Consulting (HRC) surveyed a random sample of 68 Twin Cities construction companies to find information on the costs of their health care plans. One of the items being tracked is the annual deductible that employees must pay. The Minnesota Department of Labor reports that historically the mean deductible amount per employee is $499 with a standard deviation of $80.
What is the chance HRC finds a sample mean between $477 and $527?
Calculate the likelihood that the sample mean is between $492 and $512.
Answers
part a.
There is a 49.1% chance that HRC finds a sample mean between $477 and $527.
part b.
There is a 20.9% chance that the sample mean falls between $492 and $512.
How do we calculate?The standard error (SE) of the sample mean.
SE = σ / √(n)
σ = $80 and n = 68.
SE = 80 / √(68)
z1 = (X1 - μ) / SE
z2 = (X2 - μ) / SE
for first scenario:
X1 = $477, X2 = $527, and μ = $499.
z1 = (477 - 499) / SE
z2 = (527 - 499) / SE
For the range $477 to $527:
z1 = (477 - 499) / SE
z2 = (527 - 499) / SE
z1 = -0.275
z2 = 0.35
Probability 1 = 0.4909 = 49.1%
We have a 49.1% chance that HRC finds a sample mean between $477 and $527.
For the second scenario
X1 = $492, X2 = $512, and μ = $499.
z1 = (492 - 499) / Standard Error
z2 = (512 - 499) / SE
We have a 20.9% chance that the sample mean falls between $492 and $512.
Learn more about standard error at:
https://brainly.com/question/1191244
#SPJ1
Does this set of ordered pairs represent a function? (-1,5)(0,-3)(2,7)(4,0)(7,5)
Answers
Answer:
No
Step-by-step explanation:
You cant have 2 y values
Answer:
it is indeed a function
Step-by-step explanation:
Solve the equation for x.
X-5 = 11
Enter the number that belongs in the green box.
x = [?]
Enter
Answers
One small question in attached, shouldn't take long. thanks for help

Answers
The thickness (in millimeters) of the coating applied to hard drives is one characteristic that determines the usefulness of the product. When no unusual circumstances are present, the thickness (x) has a normal distribution with a mean of 2 mm and a standard deviation of 0.04 mm. Suppose that the process will be monitored by selecting a random sample of 25 drives from each shift's production and determining x, the mean coating thickness for the sample.
Required:
Describe the sampling distribution of X (for a sample of size 16).
Answers
Answer:
The sampling distribution of X, for a sample of size 16, will be approximately normal with mean 2 mm and standard deviation 0.01 mm.
Step-by-step explanation:
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For the population:
Mean 2 mm, standard deviation 0.04 mm
Describe the sampling distribution of X (for a sample of size 16).
Sample of size 16 means that \(n = 16\)
By the Central Limit Theorem, approximately normal with mean 2 and standard deviation \(s = \frac{0.04}{\sqrt{16}} = 0.01\)
Solution:
4 The music teacher has $75. He buys 4 folk song
books that cost $9 each. Does he have enough
money left to buy a music stand for $49? If not, how
much more money does he need?
Show your work.
34
10
105
36
Answers
Answer:
10
Step-by-step explanation:
4(folk songs) × $9 = 36
36 + $49 = 85
85 - 75 = 10
Answer: No He will need $10.00 more.
Step-by-step explanation:
4 books X $9. = $36.000
$75. - 36. = $39.00
He will need $10.00 more to buy the $49.00 music stand.
Solve 3x - 2y = - 6 if the domain is {-2, -1, 0, 2, 3).
Write your answer as ordered pairs.
Answers
The solution of equation as ordered pairs can be given as {0, 3/2, 3, 6, 15/2}.
Domain may be defined as the input variable x for any of the given function which gives a suitable set of output variables y. The input variable is called the independent variable whereas the output variable is called the dependent variable. The equation given in the question 3x - 2y = -6 can also be expressed as y = (3x + 6)/2. The ordered pairs of Domain are {-2, -1, 0, 2, 3}. Now if we put these values as values of x we get the values of y as,
At x = -2, y = 0, at x = -1, y = 3/2, at x = 0, y = 3, at x = 2, y = 6 and at x = 3, y = 15/2.
These are the values of outputs, and the ordered pair will be expressed as
{0, 3/2, 3, 6, 15/2}.
Learn more about Domain at:
brainly.com/question/13109733
#SPJ1
the 4 winning numbers in a swimming club lottery were called out as follows the 1st number is the square root of 576 the 2nd number is a multiple of 8 between 30 and 39 the 3rd number is the cube of 3 the 4th number is the largest prime number less than 40 what we’re the 4 winning numbers?
Answers
The four winning numbers are 24, 32, 27 and 37 respectively
How to determine the numbersIt is important to note the following;
A prime number is a number than is divisible by 1 and itselfA square root is defined as the factor of a number which when multiplied by itself would give back the original numberThe cube of a number is that number to the exponent or power of 3A multiple is defined as the product of an integer, element or quantityFrom the information given;
a. First number = square root of 576
This is represented as
First number = √576
First number = 24
b. Second number = multiple of 8 between 30 and 39
Second number = 32
c. Third number = cube of 3
This is represented as;
Third number = 3³
Third number = 37
d. largest prime number less than 40
Fourth number = 37
Hence, the numbers are 24, 32, 27 and 37
Learn more about prime numbers here:
https://brainly.com/question/145452
#SPJ1
A teacher wants to determine how to sit 30 students in a classroom.
What simulation can be used to determine where the students sit?
A. A coin is used and assigned for every two students.
B. A six-sided number cube and every 6 students are assigned to a side.
C. A random number generator where each student is assigned a number.
D. A standard deck of cards is used and students are assigned to the cards.
Helppppp
Answers
Answer:
c is the best one to choose because it makes the most since
36 apartments on 9 floors = apartments per floor
Answers
Answer:
4 apartments per floor
Answer: 4
Step-by-step explanation:
If there are 36 apartments in the building with 9 on each floor, you can find the answer by simply doing the equation 36/9=4.
The inverse of the function
f(x)=(x+1)^2+2 if x ≥ 0 is
Answers
If \(f^{-1}(x)\) is the inverse of \(f(x)\), then
\(f\left(f^{-1}(x)\right) = x\)
We're given a domain for \(f(x)\) of \(x\ge0\), so \(f\left(f^{-1}(x)\right) = x\) is valid only for \(f^{-1}(x)\ge0\).
Now,
\(f\left(f^{-1}(x)\right) = \left(f^{-1}(x) + 1\right)^2 + 2 = x\)
Solve for the inverse :
\(\left(f^{-1}(x) + 1\right)^2 = x - 2 \\\\ \sqrt{\left(f^{-1}(x)+1\right)^2} = \sqrt{x-2} \\\\ \left|f^{-1}(x) + 1\right| = \sqrt{x-2}\)
Since \(f^{-1}(x)\ge0 \implies f^{-1}(x)+1 \ge0\), by definition of absolute value we have
\(\left|f^{-1}(x)+1\right| = f^{-1}(x) + 1\)
Then we end up with
\(f^{-1}(x) + 1 = \sqrt{x-2} \\\\ \boxed{f^{-1}(x) = \sqrt{x-2}-1}\)
A group of students conducted several trials of an experiment to study Newton’s second law of motion. They concluded that tripling the mass required tripling the net force applied. What quantity were the students holding constant?
net force
acceleration <-- MY ANSWER
number of trials
mass
Answers
Answer:
Acceleration
Step-by-step explanation:
The Newton's second law of motion can be expressed as;
F = ma
Where F is the force acting on an object, m is the mass of the object and a is the acceleration of the object.
For an object of mass 2kg and acceleration of 5 m/\(s^{2}\), we have;
\(F_{1}\) = 2 × 5 = 10 N
If we triple the mass,
m = 2 × 3 = 6 kg
Therefore,
\(F_{2}\) = 6 × 5 = 30 N
Thus, at constant acceleration, \(F_{2}\) = 3 × \(F_{1}\)
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2