Graph the image of the polygon after a reflection in the line y = -x .
A=(-3,2)
B=(1,-1)
C=(-2,-2)
D=(-4,-1)

Answers
The image of the polygon after a reflection in the line y = -x is attached below.
What is geometric transformation?It is defined as the change in coordinates and the shape of the geometrical body. It is also referred to as a two-dimensional transformation. In the geometric transformation, changes in the geometry can be possible by rotation, translation, reflection, and glide translation.
It is given that the coordinate of the polygon is A=(-3,2), B=(1,-1) , C=(-2,-2) and D=(-4,-1)
The y-coordinate of a point that is reflected across the y-axis stays constant, but the x-coordinate is assumed to be the additive inverse. Point (x, y) is reflected across the y-axis, and the result is
Thus, the image of the polygon after a reflection in the line y = -x is attached below.
Learn more about the geometric transformation here:
brainly.com/question/16156895
#SPJ1

Related Questions
y=4x a proportionail relationship
Answers
Answer:
If you are asking if y = 4x is proportional, the answer is yes. It is linear and it goes through the origin.
Step-by-step explanation:

the sides of an equilateral triangle are increasing at a rate of 10cm/min. at what rate is the area of the triangle increasing when the sides are 30cm long?(3.9
Answers
The area of the triangle is increasing at a rate of 450sqrt(3) cm²/min.
What is the rate at which the area of an equilateral triangle is increasing?
To find the rate at which the area of the equilateral triangle is increasing, we first need to know the formula for the area an equilateral triangle, which is:
of
Area = (sqrt(3)/4) x (side)²
where side is the length of one of the sides of the equilateral triangle.
We are given that the sides of the equilateral triangle are increasing at a rate of 10cm/min. This means that at any given time t, the length of each side is given by:
side = 30 + 10t
We want to find the rate at which the area of the triangle is increasing when the sides are 30cm long. This means that we need to evaluate the derivative of the area formula with respect to time t when side = 30. Taking the derivative of the area formula, we get:
dA/dt = (sqrt(3)/2) x side x (d(side)/dt)
Substituting side = 30 + 10t and d(side)/dt = 10, we get:
dA/dt = (sqrt(3)/2) x (30 + 10t) x 10
When t = 0 (i.e. when the sides are 30cm long), we get:
dA/dt = (sqrt(3)/2) x (30) x 10 = 450sqrt(3)
Therefore, when the sides of the equilateral triangle are increasing at a rate of 10cm/min and are 30cm long, the area of the triangle is increasing at a rate of 450sqrt(3) cm²/min.
Learn more about triangle
brainly.com/question/29083884
#SPJ11
Please Help! 60 points for a rapid reply- please look at the question below= The Figure of circle A shown has a diameter of PR which intersects with QS at point B and the measurements shown, Calculate the following measures-


Answers
The measures in the circle given in the image above are calculated as:
1. m<PSQ = 130°; 2. m<AQS = 30°; 3. m(QR) = 100°; 4. m(PS) = 110°; 5. (RS) = 70°.
How to Find the Measures in the Circle?In order to find the measures in the circle shown, recall that according to the inscribed angle theorem, the measure of intercepted arc is equal to the central angle, but is twice the measure of the inscribed angle.
1. m<PSQ = m<PAQ
Substitute:
m<PSQ = 130°
2. Find m<PBQ:
m<PBQ = 1/2(m(PQ) + m(RS)) [based on the angles of intersecting chords theorem]
Substitute:
m<PBQ = 1/2(130 + 2(35))
m<PBQ = 100°
m<AQS = 180 - [m<BAQ + m<PBQ]
Substitute:
m<AQS = 180 - [(180 - 130) + 100]
m<AQS = 30°
3. m(QR) = m<QAR
Substitute:
m(QR) = 100°
4. m(PS) = 180 - m(RS)
Substitute:
m(PS) = 180 - 2(35)
m(PS) = 110°
5. m(RS) = 2(35)
m(RS) = 70°
Learn more about Measures in a Circle on:
https://brainly.com/question/27111486
#SPJ1
Are the following triangles congruent? If so, how do you know why?
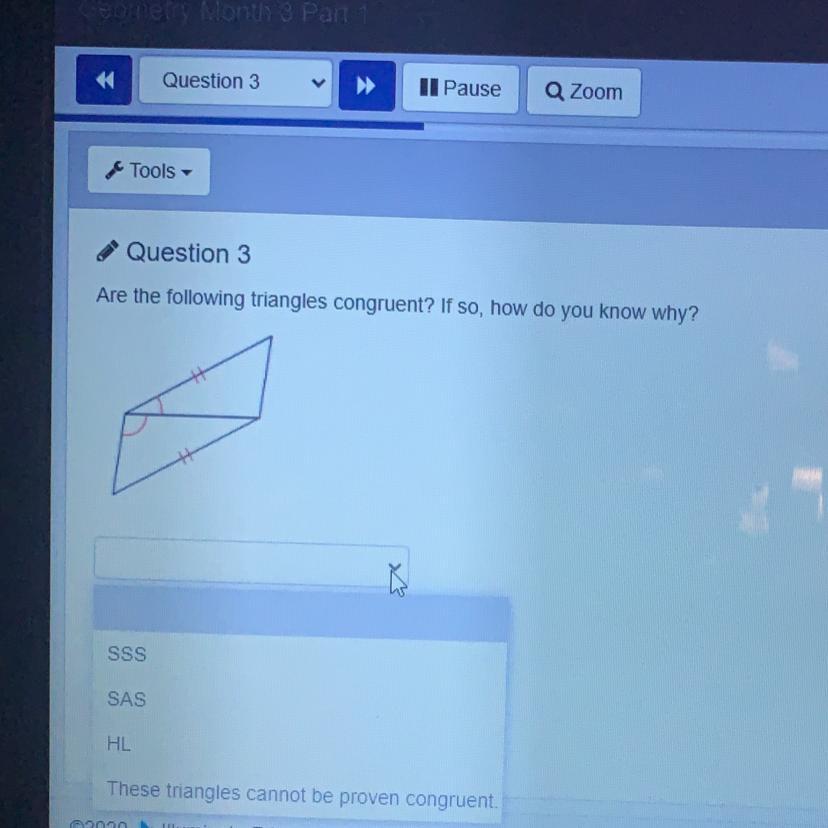
Answers
Answer:
Step-by-step explanation:When two triangles are congruent they will have exactly the same three sides and exactly the same three angles. The equal sides and angles may not be in the same position (if there is a turn or a flip), but they are there.
Evaluate the double integral. D (2x + y) dA, D = {(x, y) | 1 ≤ y ≤ 2, y − 1 ≤ x ≤ 1}.
Answers
The value of the double integral of (2x + y) dA over the region D = {(x, y) | 1 ≤ y ≤ 2, y − 1 ≤ x ≤ 1} is 3.
1. Identify the region D: {(x, y) | 1 ≤ y ≤ 2, y − 1 ≤ x ≤ 1}.
2. Set up the double integral: ∬_D (2x + y) dA = ∫(1 to 2)∫(y-1 to 1) (2x + y) dxdy.
3. Integrate with respect to x: ∫(1 to 2) [x² + xy] (from y-1 to 1) dy.
4. Evaluate the antiderivative at the bounds: ∫(1 to 2) [(1+y) - (y²-y)] dy.
5. Simplify the integrand: ∫(1 to 2) (2 - y² + 2y) dy.
6. Integrate with respect to y: [(2y - (1/3)y³ + y³)] (from 1 to 2).
7. Evaluate the antiderivative at the bounds: [(4 - (8/3) + 8) - (2 - (1/3) + 1)] = 3.
To know more about double integral click on below link:
https://brainly.com/question/31404551#
#SPJ11
a store is having a sale on trail mix and jelly beans. For 5 pounds of trail mix and 6 pounds of jelly beans, the total cost is $23. For 3 pounds of trail kix and 2 pounds of jelly beans, the total cost is $11. Find the cost for each pound of traol mix and each pound of jelly beans
Answers
Answer:
j=$1.75/lb
t=$2.5/lb
Step-by-step explanation:
(1) 5t+6j=23
(2) 3t+2j=11, t=11/3 - 2j/3
sub t into (1):
5(11/3 - 2j/3) +6j = 23
55/3 -10j/3 +6j =23
8j/3=14/3
8j=14
j=7/4
sub j into t:
t=11/3 -2(7/4)/3
t=5/2
Plz anwer i give 30 points or 20

Answers
Answer:
x = -6
hope this helps!
Answer:
the answer should be letter B your welcome ;)
Step-by-step explanation:
Which is the best estimate for the average rate of change for the quadratic function graph on the interval 1 ≤ x ≤ 3?

Answers
Answer:
I think it's either 1/2 or 1/3.
I'll give you 20 points please help and don't give a fake answer I don't wanna fail

Answers
Answer:
g(x) = 8x -15
Step-by-step explanation:
g(x) = 8(x-2) +1
= 8x -16 +1
= 8x -15
If a is an odd number, b an even number, and c an odd number, which expression will always be equivalent to an odd number?
Answers
a + c
a - c
c + a
c - a
a + c
a - c
c + a
c - a
In all of these expressions, the sum or difference of two odd numbers is always an odd number, so the result will always be an odd number.
On the other hand, the following expressions will always be equivalent to an even number:
a + b
a - b
b + a
b - a
a + b
a - b
b + a
b - a
In all of these expressions, the sum or difference of an odd number and an even number is always an even number, so the result will always be an even number.
all whole numbers are natural nummbers
Answers
Answer:
it starts from 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and so on. But all whole numbers are not natural numbers.
a confidence interval has a critical value (z*) of 1.96. if the margin of error is 0.022, what is the standard error? round to 3 decimal points (e.g. 0.045).
Answers
With a critical value of 1.96 and a margin of error of 0.022, the standard error is 0.011.
To find the standard error, we can use the formula for the margin of error, which is:
Margin of Error = Z* × Standard Error
Given that the margin of error is 0.022 and the critical value (Z*) is 1.96, we can rearrange the formula to find the standard error:
Standard Error = Margin of Error / Z*
Standard Error = 0.022 / 1.96
Standard Error = 0.011224
Rounded to three decimal points, the standard error is 0.011.
Given a confidence interval with a critical value of 1.96 and a margin of error of 0.022, the standard error is approximately 0.011.
To know more about standard error, click here
https://brainly.com/question/13179711
#SPJ11
Factor the trinomial represented by the algebra tiles.
2
The result is
11
11
XXXX
XXX

Answers
The factor form of two possible trinomials representing the tiles are: (i) y = (x - 7) · (x + 1), (ii) y = (x + 7) · (x - 1).
How to derive the trinomial and its factor form
In this problem we find a tile representing a trinomial, a quadratic equation of the form y = A · x² + B · x + C, where A, B, C are real coefficients. The number of blue squares indicates that A = 1, the number of yellow squares indicates that B = 6 and the number of green rectangles indicates that C = 7.
In addition, the quadratic equation can be factored in two ways if the following signs are included in the given coefficients:
A = 1, B = - 6, C = - 7
Standard form: y = x² - 6 · x - 7
Factor form: y = (x - 7) · (x + 1)
A = 1, B = 6, C = - 7
Standard form: y = x² + 6 · x - 7
Factor form: y = (x + 7) · (x - 1)
To learn more on trinomials: https://brainly.com/question/16347049
#SPJ1
12.34
the measure of one interior angle of a rhombus is \(79^{\circ}\) . what are the measures of the other three interior angles?
Answers
Step-by-step explanation:
a rhombus is a parallelogram with 4 identical sides.
it has therefore two pairs of equal angles.
as any quadrilateral the sum of all interior angles is 360°.
(and yes, as add-on, the diagonals bisect each other at right angles).
so, one interior angle is 79°.
that means it has a twin that is also 79°.
together they have 79×2 = 158°.
that leaves
360 - 158 = 202°
for the other 2 angles (they must be equal too).
so, each of them has
202/2 = 101°
so, the other 3 angles are
79°, 101°, 101°
Construct a 90% confidence interval for the population mean you. Assume the population has a normal distribution a sample of 15 randomly selected math majors had mean grade point average 2.86 with a standard deviation of 0.78
Answers
The 90% confidence interval is: (2.51, 3.22)
Confidence interval :It is a boundary of values which is eventually to comprise a population value with a certain degree of confidence. It is usually shown as a percentage whereby a population means lies within the upper and lower limit of the provided confidence interval.
We have the following information :
Number of students randomly selected, n = 15.Sample mean, x(bar) = 2.86Sample standard deviation, s = 0.78Degree of confidence, c = 90% or 0.90The level of significance is calculated as:
\(\alpha =1-c\\\\\alpha =1-0.90\\\\\alpha =0.10\)
The degrees of freedom for the case is:
df = n - 1
df = 15 - 1
df = 14
The 90% confidence interval is calculated as:
=x(bar) ±\(t_\frac{\alpha }{2}\), df \(\frac{s}{\sqrt{n} }\)
= 2.86 ±\(t_\frac{0.10 }{2}\), 14 \(\frac{0.78}{\sqrt{15} }\)
= 2.86 ± 1.761 × \(\frac{0.78}{\sqrt{15} }\)
= 2.86 ± 0.3547
= (2.51, 3.22)
Learn more about Confidence interval at:
https://brainly.com/question/32546207
#SPJ4
find the taylor series for f centered at 7 if f (n)(7) = (−1)nn! 2n(n 1) .
Answers
Therefore, the Taylor series for f centered at 7 is given by: \(f(x) = (-1)^n * n! * 2^n * (n-1) + (-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (x-7) + (-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4) * (x-7)^2/2 + (-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4) * (n-5) * (n-6) * (x-7)^3/6 + ...\)
To find the Taylor series for f centered at 7, we can use the formula for the Taylor series expansion:
\(f(x) = f(c) + f'(c)(x-c) + (f''(c)(x-c)^2)/2! + (f'''(c)(x-c)^3)/3! + ...\\f(x) = f(c) + f'(c)(x-c) + (f''(c)(x-c)^2)/2! + (f'''(c)(x-c)^3)/3! + ...\\f'(x) = -(-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (x-7)^{(n-3)}\\f''(x) = -(-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4) * (x-7)^{(n-5)}\\f'''(x) = -(-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4) * (n-5) * (n-6) * (x-7)^{(n-7)\)
Now let's evaluate these derivatives at x = 7:
\(f(7) = (-1)^n * n! * 2^n * (n-1)\\f'(7) = -(-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2)\\f''(7) = (-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4)\\f'''(7) = -(-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4) * (n-5) * (n-6)\)
Now we can substitute these values into the Taylor series expansion formula:
\(f(x) = f(7) + f'(7)(x-7) + (f''(7)(x-7)^2)/2! + (f'''(7)(x-7)^3)/3! + ...\)
Simplifying further, we get:
\(f(x) = (-1)^n * n! * 2^n * (n-1) + (-1)^n * n! * 2^(n-1) * (n-1) * (n-2) * (x-7) + (-1)^n * n! * 2^(n-1) * (n-1) * (n-2) * (n-3) * (n-4) * (x-7)^2/2 + (-1)^n * n! * 2^{(n-1)} * (n-1) * (n-2) * (n-3) * (n-4) * (n-5) * (n-6) * (x-7)^3/6 + ...\)
To know more about Taylor series,
https://brainly.com/question/32291357
#SPJ11
Please help due at 10:00!!!!!!!!!!!

Answers
3y = 5
6 = 2x + 2
x = 2, y = 5/3
2x - 2 = 2 ←
Answer:
y = - 4
Step-by-step explanation:
3y = 2x - 6 ................. (1)
4x + 3y = - 24 ........... (2)
(1) ----> (2)
4x + ( 2x - 6 ) = - 24
6x - 6 = - 24
x - 1 = - 4
x = - 3
3y = 2 ( - 3 ) - 6
3y = - 12
y = - 4
( - 3 , - 4 )
PLEASE HELP WITH MATH

Answers
Answer:
1/15
Step-by-step explanation:
Multiply 1/5 by 3, therefore making this problem 3/15 - 2/15 = _. Subtract to get 1/15
1. Find the area of the figure above in square inches
2. Find the perimeter of the figure above in inches

Answers
Statistical data of car accidents show that the annual vehicle miles (i.e., miles per vehicle per year) driven between traffic accident can be presented by a mean of 15,000 miles per year and standard deviation of 3750 miles per year. Z distribution.pdf For a typical driver who drives less than 10,000 miles per year, the probability of him/her having an accident in a year is _____________.
Answers
The probability of a typical driver who drives less than 10,000 miles per year having an accident in a year is 9.18%.
To calculate the probability of a driver who drives less than 10,000 miles per year having an accident, we can use the Z-score and the standard normal distribution.
First, we need to calculate the Z-score for a driver who drives less than 10,000 miles per year. The Z-score formula is:
Z = (X - μ) / σ
Where:
X is the value we want to calculate the Z-score for (10,000 miles per year),
μ is the mean (15,000 miles per year), and
σ is the standard deviation (3,750 miles per year).
Plugging in the values, we get:
Z = (10,000 - 15,000) / 3,750
Z = -1.333
Looking up the Z-score -1.333 in the standard normal distribution table, we find the probability to be approximately 0.0918 or 9.18%.
Therefore, the probability of a typical driver who drives less than 10,000 miles per year having an accident in a year is approximately 9.18%.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ4
What is thee answer to this?

Answers
Answer:
160 packages in 4 minutes
Step-by-step explanation:
If this helped please mark brainliest
A fast food chain operation is interested in determining whether the mean per customer purchase differs by day of the week. To test this, it has e selected random samples of customers for each day of the week. The analysts then ran a one-way analysis of variance generating the following output:
Answers
Based on the output (B) there is no basis for concluding that mean sales are different for the different days of the week.
What are random samples?A simple random sample (or SRS) in statistics is a subset of individuals (a sample) chosen at random from a larger set (a population) with the same probability. It is the process of selecting a sample at random. In SRS, each subset of k people has the same chance of being chosen for the sample as any other subset of k people. An unbiased sampling technique is a simple random sample. Simple random sampling is a fundamental type of sampling that can be used to supplement more complex sampling methods.According to the given table, There is no basis for concluding that mean sales are different for the different days of the week.
Therefore, based on the output (B) there is no basis for concluding that mean sales are different for the different days of the week.
Know more about random samples here:
https://brainly.com/question/24466382
#SPJ4
The complete question is given below:
A fast food chain operation is interested in determining whether the mean per customer purchase differs by day of the week. To test this, it has selected random samples of customers for each day of the week. The analysts then ran a one-way analysis of variance generating the following output:
Based upon this output, which of the following statements is true if the test is conducted at the 0.05 level of significance?
(A) Based on the p-value, the null hypothesis should be rejected since the p-value exceeds the alpha level.
(B) There is no basis for concluding that mean sales is different for the different days of the week.
(C) Based on the critical value, the null should be rejected.
(D) The experiment is conducted as an unbalanced design.

find the value of x *

Answers
Answer:
5 2/5 seems right to me
Step-by-step explanation:
filler filler filler
T/F: The proportion in the body of a normal distribution can never be less than 0.50.
Answers
This statement ''The proportion in the body of a normal distribution can never be less than 0.50.'' is false because the proportion in the body of a normal distribution can be less than 0.50, depending on the location of the mean and the spread of the distribution.
In fact, for a normal distribution with a mean of μ and standard deviation of σ, approximately 68% of the area under the curve falls within one standard deviation of the mean (i.e., between μ - σ and μ + σ), which means the proportion in the body of the distribution is about 0.68.
The remaining 32% is split evenly between the tails of the distribution, which means the proportion in each tail is about 0.16.
So, the proportion in the body of the distribution is greater than 0.50.
To know more about normal distribution refer here:
https://brainly.com/question/15103234#
#SPJ11
How does the structure of each poem help to convey different feelings

Answers
The fraction of the total vote he should expect to get is 23/75.
What are fractions?A fraction is a mathematical unit used to represent a portion of a whole or a ratio of two integers. They are shown as the top number, or numerator, and the bottom number, or denominator, separated by a line. The denominator is the total number of pieces that make up the whole, whereas the numerator is the number of shares or parts.
For instance, you may write 3/8 for the portion of pizza you consumed if there were 8 pieces and you only ate 3. This indicates that you consumed three of the pizza's eight equally sized portions.
From the given table we can determine the total number of votes are:
13 + 9 + 10 + 8 + 10 + 14 + 5 + 6 = 75.
Now, Jamal received 13 + 10 = 23 votes.
Thus, the fraction of the total vote he should expect to get is 23/75.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ1
michael is 3 33 times as old as brandon. 18 1818 years ago, michael was 9 99 times as old as brandon. how old is brandon now?
Answers
Brandon is currently 6 81 years old.
Let M be Michael's age and B be Brandon's age.
We are given that Michael is 3 33 times as old as Brandon. This means that M = 3 33 × B
We are also given that 18 1818 years ago, Michael was 9 99 times as old as Brandon. This means that M - 18 1818 = 9 99 × (B - 18 1818).
We can combine these two equations to solve for Brandon's current age:
3 33 × B = (9 99 × B) + 18 1818
2 66 × B = 18 1818
B = 18 1818 / 2 66 = 6 81.
Therefore, Brandon is currently 6 81 years old.
Learn more about equations here:
https://brainly.com/question/10413253
#SPJ4
h(x) = 4x +3. What is
the coordinate pair for h (1)?
Answers
9514 1404 393
Answer:
(1, 7)
Step-by-step explanation:
Fill in x=1 and do the arithmetic.
h(1) = 4(1) +3 = 7
The coordinate pair is ...
(x, h(x)) = (1, h(1)) = (1, 7)
Determine the values of r for which the given differential equation has solutions of the form y=e^(rt) . Give the answers in ascending order. y ′′′−8y ′′ +15y ′ =0. - r={0,1,5} - r={0,2,3} - r={2,3} - r={0,3,5} - None of the given choices.
Answers
Given differential equation: y''-8y'+15y=0We are to determine the values of r for which the given differential equation has solutions of the form y=e^(rt).
We know that the characteristic equation is given by ar^2+br+c=0, where a,b and c are coefficients of the differential equation.
Now let's solve this using the characteristic equation.r^2 -8r+15=0Factor the quadratic equation(r-5)(r-3)=0 Therefore, r=5 or r=3 or r=0.
Thus, we obtain the following values of r for which the given differential equation has solutions of the form y=e^(rt):r={0,3,5}.So, the correct option is:r={0,3,5}.
Learn more about differential
https://brainly.com/question/31383100
#SPJ11
5 Andrew saves the same amount of money each week. The table shows the amount he saves in different numbers of weeks. How much money does Andrew save in 40 weeks? Show your work. Week 7 9 11
Answers
Answer:
hw could make 200 dollars in 4 weeks
A level machine is used to perform the differential leveling between a benchmark and a target point with a closed loop, and get four backsight values as 7.85 ft, 3.55 ft, 4.51 ft and 5.01 ft and four foresight values as 5.57 ft, 3.87 ft, 5.15 ft and 6.11 ft What is the error of closure (EC)? a) None of the given answers b) -0.22 ft Oc) 0.22 ft d) 0.06 ft e) -0.06 ft
Answers
The error of closure (EC) is a measure of the accuracy of a closed loop leveling survey.
To calculate the error of closure, we need to subtract the sum of the foresight values from the sum of the backsight values. In this case, the sum of the backsight values is (7.85 ft + 3.55 ft + 4.51 ft + 5.01 ft) = 20.92 ft, and the sum of the foresight values is (5.57 ft + 3.87 ft + 5.15 ft + 6.11 ft) = 20.70 ft.
The error of closure (EC) can be obtained by subtracting the sum of the foresight values from the sum of the backsight values: EC = (sum of backsight values) - (sum of foresight values) = 20.92 ft - 20.70 ft = 0.22 ft.
Therefore, the correct answer is c) 0.22 ft, which represents the error of closure in this leveling survey.
To know more about error of closure click here: brainly.com/question/31500248
#SPJ11