Hannah can spend up to $40 on snacks and drinks at the movie theater. A snack costs $5 and a drink costs $3.50.
Use for the number of snacks
Use for the number of drinks
Which inequality represents this situation?

Answers
Answer:
5s + 3.50d < 40
Step-by-step explanation:
if you were to total up the costs of a snack and drink together you'll end up with $8.50
-multiply $8.50 until you reach $40 mark
i.e 8.50×2(means 2 of each item) = $17
8.50×3 = $25.5
8.50×4 = $34
8.50×5= $42.5
-if you look at it, the calculation for 5, the pricing is now over the budget therefore the answer is then 5s + 3.50d < 40 because she can only spend up to $34 at most
Related Questions
Consider triangle HJL, where line HK is the perpendicular bisector of segment JL. Which additional piece of information is needed to prove HJKandHLK BY THE SIDE-side-side congruence theorem

Answers
Given
Answer
Since it is given
KJ=KL
HK=HK (Common)
The only condition to show SSS congruency is HJ = HL

PLEASE HELP!! WILL GIVE BRAINLIEST IF YOU ANSWER SOON!!!
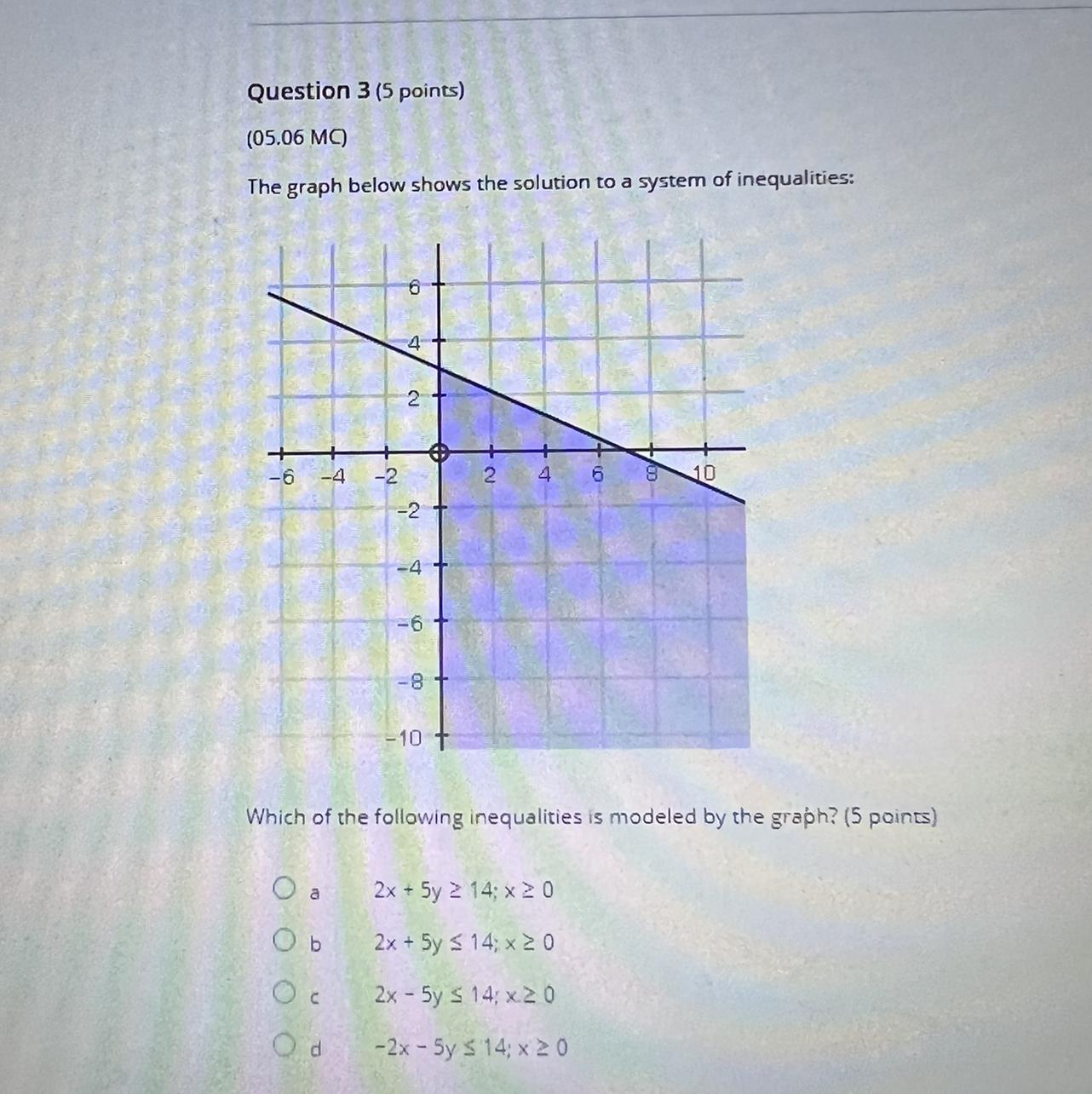
Answers
Answer:
b
Step-by-step explanation:
math
what is the answer for -40= -50 + x ?
Answers
Answer:10
Step-by-step explanation: Because negative 40 equals -50 + x equals 10
Don’t know what the answer is

Answers
Answer:
48.3 miles
Step-by-step explanation:
"each" is the key word here. When you see "each" in a word problem, you should know to multiply. 6.9 times 7 is 48.3.
Answer:
48.3 miles in 7 days
Step-by-step explanation:
Step 1:
6.9 miles × 7 days Equation
Step 2:
6.9 × 7 Multiply
Answer:
48.3 miles in 7 days
Hope This Helps :)
Find the length of a hypotenuse for a right triangle with legs 3 and 3. Round your answer to the nearest hundredth.
Answers
Answer:
H=4.243
Step-by-step explanation:
Formula: A^2+B^2=C^2
(3)^2+(3)^2=C^2
9+9=C^2
sqrt18=C
C=4.242640....
Question 2
Find the equation of the line parallel to y = x - 2 that passes through the point (-3,2).
Answers
Answer:
The equation of the required line is y = x + 5
Step-by-step explanation:
The equation of the given line is y = x - 2
The required line = A line parallel to the given line
The point through which the required line passes = (-3, 2)
The general form of the equation of a straight line, is y = m·x + c
Where;
m = The slope of the line
By comparison, the slope of the given line, m = 1
When two lines are parallel, their slope are equal
Therefore, the slope of the required line = m = 1
The equation of the required line in point and slope form is therefore;
y - 2 = x - (-3) = x + 3
∴y = x + 3 + 2 = x + 5
The equation of the required line is therefore;
y = x + 5.
Compare the investment below to an investment of the same principal at the same rate compounded annually.
principal: $9,000, annual interest: 6%, interest periods: 12, number of years: 14
After 14 years, the investment compounded periodically will be worth $ (Round to two decimal places as needed.)
more than the investment compounded annually.
Answers
As a result, after 14 years, the investment that was compounded interest irregularly will be valued $961.54 more than the one that was compounded yearly.
what is interest ?By dividing the principal by the interest rate, the passage of time, and other factors, simple interest is determined. Simple return equals principle plus interest plus hours is the formula used in marketing. The easiest way to compute interest is by using this method. The most typical method for calculating interest is as a portion of the principle amount. For example, if he borrows $100 from a buddy and agrees to pay back the loan at 5% interest, he will only pay his share of the 100% interest. $100 (0.05) = $5. When you borrow money, you must pay interest, and you must charge interest when you lend it. Typically, interest is determined as an annual percentage of the loan total. The loan's interest is the name given to this percentage.
We must apply the compound interest calculation in order to compare the values of the investment compounded annually with the investment compounded periodically:
\(A = P(1 + r/n)^(nt) (nt)\)
where:
A is the total sum.
The principal is P. (the initial amount)
n is the number of times the interest is compounded each year, and r is the yearly interest rate (expressed as a decimal).
The number of years is t.
We have the following for the yearly compounded investment:
\(A = 9000(1 + 0.06/1)^(1*14) = $20,207.97\)
Periodically compounded investment results in:
\(A = 9000(1 + 0.06/12)^(12*14) = $21,168.51\)
As a result, after 14 years, the investment that was compounded irregularly will be valued $961.54 more than the one that was compounded yearly.
To know more about interest visit:
https://brainly.com/question/28792777
#SPJ1
find the percent of 0.20 to 0.50
Answers
answer: 40
explanation: Solution for 0.20 is what percent of 0.50: 0.20:0.50*100 = (0.20*100):0.50 = 20:0.50 = 40. Now we have: 0.20 is what percent of 0.50 = 40.
bonjour;)!
0.50=100%
0.25=50%
5+5+5+5+5=50% ir 20
5=10%
5+5+5+5=40%
0.20/0.50=40%
hope it help
(a) Write an expression for a Riemann sum of a function f on an interval [a, b]. Explain the meaning of the notation that you use.
(b) If f(x)⩾ 0, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.
(c) If f(x) takes on both positive and negative values, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.
Answers
(a) The expression for a Riemann sum of a function f on an interval [a, b] is Δx = (b-a)/n
(b) If f(x)⩾ 0, then the geometric interpretation of a Riemann sum is infinity
(c) If f(x) takes on both positive and negative values, then the geometric interpretation of a Riemann sum is infinity
Riemann sums are an important tool in calculus for approximating the area under a curve. They are used to estimate the value of a definite integral, which represents the area bounded by the curve and the x-axis on a given interval. In this explanation, we will discuss the expression for a Riemann sum, its notation, and its geometric interpretation.
(a) Expression for a Riemann sum:
A Riemann sum is an approximation of the area under a curve using rectangles. We divide the interval [a, b] into n subintervals, each of length Δx=(b−a)/n. The notation used to represent this is:
Δx = (b-a)/n
(b) Geometric interpretation of a Riemann sum when f(x)⩾ 0:
If f(x) is always non-negative, the Riemann sum represents an approximation of the area between the curve and the x-axis on the interval [a, b].
Each rectangle has a positive area, which contributes to the overall area under the curve. The sum of the areas of the rectangles approaches the true area under the curve as the number of subintervals n approaches infinity.
(c) Geometric interpretation of a Riemann sum when f(x) takes on both positive and negative values:
When f(x) takes on both positive and negative values, the Riemann sum represents the net area between the curve and the x-axis on the interval [a, b].
Each rectangle may have a positive or negative area, depending on the sign of f(xi).
The positive areas represent regions where the curve is above the x-axis, and the negative areas represent regions where the curve is below the x-axis.
In conclusion, Riemann sums are used to approximate the area under a curve on an interval [a, b]. The expression for a Riemann sum involves dividing the interval into n subintervals and approximating the area under the curve using rectangles.
To know more about Riemann sum here.
https://brainly.com/question/30241844
#SPJ4
8. Evaluate the expression under the given conditions. sin(theta − ϕ); tan(theta) = 5 12 , theta in Quadrant III, sin(ϕ) = − 3 10 10 , ϕ in Quadrant IV
_____
9. Evaluate the expression under the given conditions.
sin(theta + ϕ); sin(theta) = 8/17, theta in Quadrant I, cos(ϕ) = −√5 /5, ϕ in Quadrant II
Answers
(a) The expression under the conditions sin(θ - Ф) is (5√(91) - 36) / 130.
(b)The expression under the conditions sin(θ + Ф) is 7√5/85.
8.To evaluate the expression sin(θ - Ф), we need to use the the trigonometric identities:
sin(θ - Ф) = sin(θ) × cos(Ф) - cos(θ) × sin(Ф)
tan(θ) = 5/12 (in Quadrant III)
sin(Ф) = -3/10 (in Quadrant IV)
From the given information, we can determine the values of cos(theta) and cos(Ф) using the Pythagorean identity:
cos(θ) = 1 / √(1 + tan²(θ)) cos(Ф)
= √(1 - sin²(Ф))
Let's calculate these values:
cos(θ) = 1 / √(1 + (5/12)²)
= 12 / √(169)
= 12 / 13 cos(Ф)
= √(1 - (-3/10)²)
= √(1 - 9/100)
= √(91/100)
= √(91) / 10
Now we can substitute the values into the expression sin(θ - Ф):
sin(θ - Ф) = sin(θ) × cos(Ф) - cos(θ) × sin(Ф)
= (sin(θ) × cos(Ф)) - (cos(θ) × sin(Ф))
= (5/13) × (√(91)/10) - (12/13) × (-3/10)
= (5√(91) - 36) / 130
Therefore, sin(θ - Ф) = (5√(91) - 36) / 130.
9.To evaluate the expression sin(θ + Ф), we can use the trigonometric identities:
sin(θ + Ф) = sin(θ) × cos(Ф) + cos(θ) × sin(Ф)
sin(θ) = 8/17 (in Quadrant I)
cos(Ф) = -√5/5 (in Quadrant II)
We can determine the value of cos(θ) using the Pythagorean identity:
cos(θ) = √(1 - sin²(θ))
= √(1 - (8/17)²)
= √(1 - 64/289)
= √(225/289)
= 15/17
Now we can substitute the values into the expression sin(θ + Ф):
sin(θ + Ф) = sin(θ) × cos(Ф) + cos(θ) × sin(Ф)
= (8/17) ×(-√5/5) + (15/17) × (√5/5)
= -8√5/85 + 15√5/85
= 7√5/85
Therefore, sin(θ + Ф) = 7√5/85.
To know more about expression click here :
https://brainly.com/question/24377281
#SPJ4
veterinary doctors marked 30 deer and released them. Later on they counted 150 deer, 12 of which had marks. TO the nearest whole number, find the best estimate of deer population.
Answers
Answer:
1800
Step-by-step explanation:
Consider the function f(x)=x² +1. (a) [3 marks] Approximate the area under y = f(x) on [0,2] using a right Riemann sum with n uniform sub-intervals. ₁² = n(n+1)(2+1) so that the (b) [3 marks] Simplify the Riemann sum in part (a) using the formula resulting expression involves no Σ or... notation. i=1 6 (c) [3 marks] Take the limit as n tends to infinity in your result to part (b). (d) [3 marks] Compute f f(x) dx and compare it to your result in part (c).
Answers
In the given problem, we are asked to approximate the area under the curve y = f(x) = x^2 + 1 on the interval [0,2] using a right Riemann sum with n uniform sub-intervals. We need to simplify the Riemann sum expression, take the limit as n tends to infinity, and compare the result with the definite integral of f(x) over the same interval.
(a) To approximate the area using a right Riemann sum, we divide the interval [0,2] into n sub-intervals of equal width. The right Riemann sum is given by ∑(i=1 to n) f(xi)Δx, where xi is the right endpoint of each sub-interval and Δx is the width of each sub-interval.
(b) Simplifying the Riemann sum involves evaluating f(xi) at each right endpoint xi and summing the resulting terms. In this case, f(xi) = (xi)^2 + 1, so we substitute the values of xi = 2i/n (where i ranges from 1 to n) into the expression and sum them.
(c) Taking the limit as n tends to infinity means letting the number of sub-intervals become infinitely large. In this case, the Riemann sum expression simplifies to the definite integral of f(x) over the interval [0,2]. Evaluating the integral gives the exact value of the area under the curve.
(d) Finally, we compute the definite integral of f(x) over the interval [0,2] to obtain the exact value of the area. We compare this result with the limit obtained in part (c) to see if they match.
To know more about Riemann sum here: brainly.com/question/30404402
#SPJ11
The mass of a gold atom is 3. 29\times 10^{-22}3. 29×10
−22
grams. The mass of a neutron is 1. 68\times 10^{-24}1. 68×10
−24
grams. How many times greater is the mass of a gold atom than the mass of a neutron? Write your answer in standard notation, rounding to the nearest tenth.
Answers
The mass of a gold atom is approximately 195.3 times greater than the mass of a neutron.
The given mass of a gold atom is 3.29 × 10^−22 grams, and the mass of a neutron is 1.68 × 10^−24 grams.
To find out how many times greater is the mass of a gold atom than the mass of a neutron, we need to divide the mass of the gold atom by the mass of a neutron.
The calculation is shown below,
3.29 × 10^−22 ÷ 1.68 × 10^−24 = 195.2381...
We see that the mass of a gold atom is approximately 195.2381 times greater.
Learn more about mass of neutron atom from:
https://brainly.com/question/13516292
#SPJ11
Could you find out what 352-322
Answers
Answer:
30
Step-by-step explanation:
Answer:
30
Step-by-step explanation:
your welcome.
a coin is tossed 9 times. what is the probability of getting at least one tail? express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
The probability of getting at least one tail when a coin is tossed 9 times is 0.8438. This can be calculated by adding the probability of getting 0 tails, 1 tail, 2 tails, 3 tails, 4 tails, 5 tails, 6 tails, 7 tails, 8 tails, and 9 tails together:
P(at least one tail) = P(0 tails) + P(1 tail) + P(2 tails) + P(3 tails) + P(4 tails) + P(5 tails) + P(6 tails) + P(7 tails) + P(8 tails) + P(9 tails)
= 0.0019 + 0.0156 + 0.0781 + 0.2051 + 0.3086 + 0.3086 + 0.2051 + 0.0781 + 0.0156 + 0.0019
= 0.8438
Therefore, the probability of getting at least one tail when a coin is tossed 9 times is 0.8438, which can be expressed as a decimal rounded to four decimal places.
The probability of getting at least one tail in a coin toss is 1 minus the probability of getting all heads.
The probability of getting a head in one toss is 0.5, so the probability of getting all heads in 9 tosses is 0.5^9 = 0.001953125.
So the probability of getting at least one tail is 1 - 0.001953125 = 0.998046875.
As a fraction, this can be written as 998046875/1000000000, which can be simplified to 511/512.
So the probability of getting at least one tail in 9 tosses is 0.9980 or 511/512.
You can read more about probability at https://brainly.com/question/24756209
#SPJ11
Kaitlin purchased a prepaid phone card for $20. Long distance calls cost 11 cents a minute using this card. Kaitlin used her card only once to make a long distance call. If the remaining credit on her card is $15.82 , how many minutes did her call last?
Answers
Answer: 38 minutes
Step-by-step explanation:
Hillary would like to buy a some new furniture. Rather then pay for thefurniture all at once, she decides to purchase it with an installment plan.She needs to put 12% down on the $3,210 Furniture. The remainingbalance she would pay back over the next 4 years. The monthly paymentsusing the installment plan are $68.2. What is the finance charge? Roundyour answer to the nearest cent. Do not include a dollar sign in youranswer.
Answers
the cost of the furniture is 3210
she puts 12% down
3210 x (12/100)=385.20
lets find the balance
3210-385.20=2824.80
this balance needs to be paid back in 4 years
the monthly payment is 68.20
4 years x 12 months= 48 months
48 x 68.20=3273.60
her original balance was 2824.80
the finace charge is:
327.60-2824.80=448.80
we need to round to the nearest cent which is 448.80
look at the screenshot

Answers
Answer:
x = 5
y = 2
Step-by-step explanation:
multiply by -2 the second equation and add the first equation to eliminate "x"
\(4x+5y=30\\-4x-10y=-40\)
_______________
\(-5y=-10\\y=\frac{-10}{-5} =2\)
To find "x", substitute the value of "y" in any equation. I do it in the first
\(4x+5(2)=30\)
\(4x+10=30\)
\(4x=30-10\\x=20/4=5\)
Hope this helps
Answer:
i got you
Step-by-step explanation:
first you will make the easiest equation into y=mx+b
2x=5y=20
subtract 2x from it self and 20, you will eliminate the 5 but keep the y then you will get y=2x+20
then you will substitute it into the y in the other equation 4x+5(2x+20)=30
after doin that you will multiply 5 by both the number in the parenthesis
4x+15x+100=30 add like terms 4x+15x =
19x+100=30 subtract 100 fromm itself and 30 you will get -70
-70 divided by 19x then you will get your answer
draft jsanedkhwebfkjrfkjrngkjnregjknerkgnkjerngkjerngkjenrg
Answers
Answer:
ok
Step-by-step explanation:
A store owner mixes 2 lb of candy that cost x dollars per pound with 3 lb of candy that costs $1.50 per pound. She sells the mix for $2.50 per pound.
1. How much did the 2 lb of the first type of candy cost the owner?
2. How much did the 3 lb of the second type of candy cost the owner?
3. How much did the two types of candy cost the store owner in total?
4. How much money will the store owner get if she sells all of the new mixture?
5. Write an equation to find the cost per pound of the first candy
6. Solve the equation to find the owners cost of the first candy per pound
Answers
Answer:
1. How much did the 2 lb of the first type of candy cost the owner?
2x
2. How much did the 3 lb of the second type of candy cost the owner?
3*1.5 = 4.5
3. How much did the two types of candy cost the store owner in total?
2x + 4.5
4. How much money will the store owner get if she sells all of the new mixture?
(2 + 3)*2.5 = 12.5
5. Write an equation to find the cost per pound of the first candy
2x + 4.5 = 12.5
6. Solve the equation to find the owners cost of the first candy per pound
2x + 4.5 = 12.5
2x = 8
x = 4
jokes are listed in a magazine, where one is written by a female author. If the order in which these jokes are told makes a difference in terms of how they are received, how many ways can they be delivered if a joke by a man is told first?
Answers
Answer: Let's assume that there are "m" jokes written by male authors and "f" jokes written by female authors, such that m + f = total number of jokes in the magazine.
If a joke by a man is told first, there are (m - 1)! ways to arrange the remaining m - 1 jokes written by male authors and f! ways to arrange the jokes written by the female author. The total number of ways the jokes can be delivered is (m - 1)! * f!.
So, the answer is (m - 1)! * f! ways to deliver the jokes if a joke by a man is told first.
Step-by-step explanation:
Determine the range of the following graph:

Answers
Answer:
[0,8]
Step-by-step explanation:
The lowest y value is 0
The highest y value is 8
We typically write range in interval notation
Interval notation goes from lowest value to highest value. Therfore the range is;
[0,8]
165% of the value is 3795 kg what is the original value
Answers
Answer:
Answer: 2300kg. formulate:: 3795kg/165%Calculate 3795kg/165%: : 2300kg.
Step-by-step explanation:
pleaseee help!!! find the value of x and y
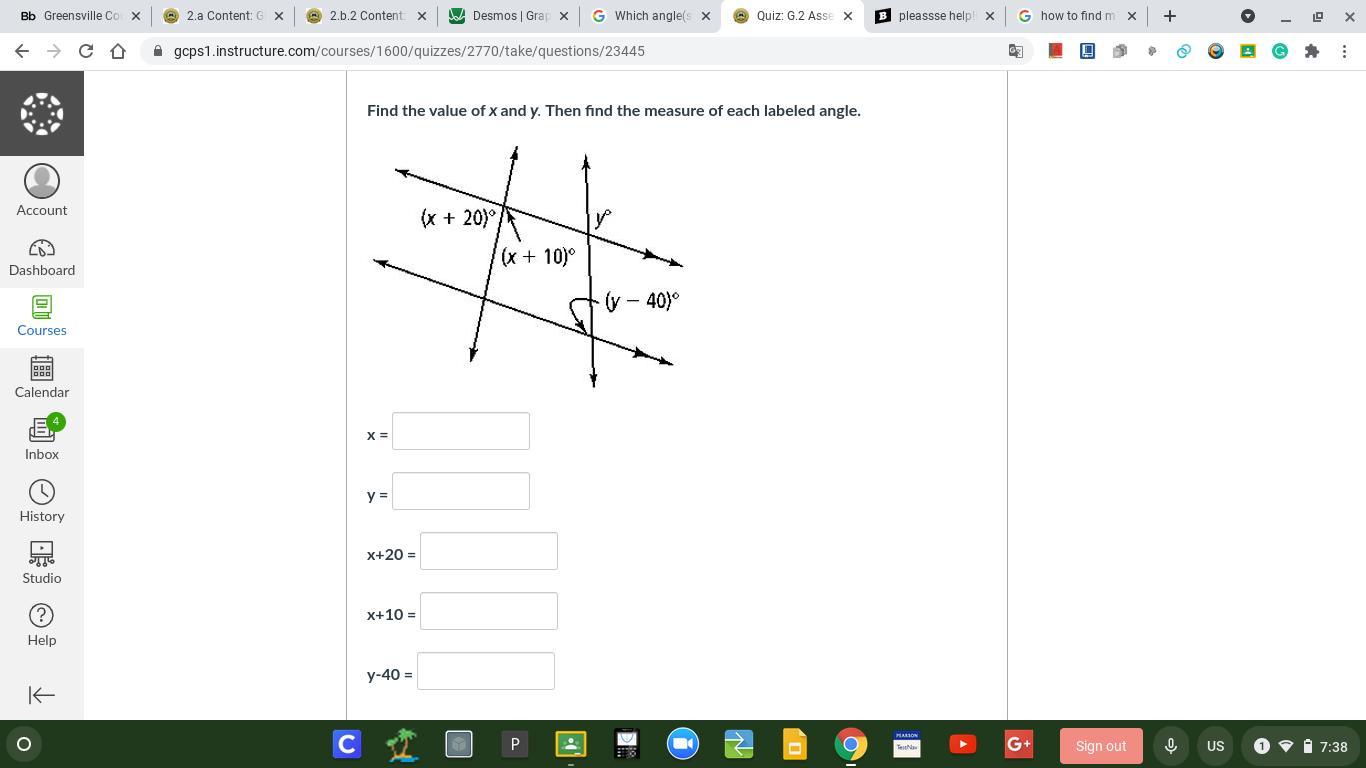
Answers
Answer:
362
Step-by-step explanation:
PLEASE SOLVE
\(\log \left(x\right)=log\left(2x^2\right)-2\)
Answers
Answer:
x = 50
Step-by-step explanation:
\(\log _{10}\left(x\right)=\log _{10}\left(2x^2\right)-2\)
\(\log _{10}\left(x\right)=\log _{10}\left(2x^2\right)-\log _{10}\left(100\right)\)
\(\log _{10}\left(x\right)=\log _{10}\left(\frac{2x^2}{100} \right)\)
\(x = \frac{2x^2}{100}\)
\(100x=2x^2\)
\(x^2 = 50x\)
\(x = 50\)
Which is NOT a function?
A y – x = 6
B y = 2x
C x = -2
D y + x = 12
Answers
Answer:
D
Step-by-step explanation:
Answer:
d
Step-by-step explanation:
Sara is building a triangular pen for her pet rabbit. If two of the sides measure 8 feet and 15 feet, the length of the third side could be
1) 13 ft
2) 7 ft
3) 3 ft
4) 23 ft
Answers
Answer:
1) 13 ft
Step-by-step explanation:
1) 13+8=21 which is greater than 15. Would be a triangle.
2) 7+8=15 This would be a single line, not a triangle.
3) 3+8<15 This would be a single line, not a triangle.
2) 15+8=23 This would be a single line, not a triangle.
Bobby goes to one store and find a Christmas tree for $49.99 the store is having a 20% off sale Bobby decide to go across the street to another store and find the same tree for $54.99 this store is having a 25% off sale what is the difference in sale prices for the tree
Answers
Answer:
1.24
Step-by-step explanation:
Solve the following:
4x-1 divided by 2= x+7
a)
b)
3x + 2 = 2x+13 divided by 3
Answers
The equation's answer is x = 7.5. 4x - 1 2 = x + 7.
x = 1 is the answer to the problem 3x + 2 = (2x + 13) 3.
a) To solve the equation 4x - 1 ÷ 2 = x + 7, we need to isolate the variable x. Let's follow the steps:
1: Distribute the division operation to the terms inside the parentheses.
(4x - 1) ÷ 2 = x + 7
2: Divide both sides of the equation by 2 to isolate (4x - 1) on the left side.
(4x - 1) ÷ 2 = x + 7
4x - 1 = 2(x + 7)
3: Distribute 2 to terms inside the parentheses.
4x - 1 = 2x + 14
4: Subtract 2x from both sides of the equation to isolate the x term on one side.
4x - 1 - 2x = 2x + 14 - 2x
2x - 1 = 14
5: Add 1 to both sides of the equation to isolate the x term.
2x - 1 + 1 = 14 + 1
2x = 15
6: Divide both sides of the equation by 2 to solve for x.
(2x) ÷ 2 = 15 ÷ 2
x = 7.5
Therefore, x = 7.5 is the solution to the equation 4x - 1 ÷ 2 = x + 7. However, note that this answer is not an integer, so it may not be valid for certain contexts.
b) To solve the equation 3x + 2 = (2x + 13) ÷ 3, we can follow these steps:
1: Distribute the division operation to the terms inside the parentheses.
3x + 2 = (2x + 13) ÷ 3
2: Multiply both sides of the equation by 3 to remove the division operation.
3(3x + 2) = 3((2x + 13) ÷ 3)
9x + 6 = 2x + 13
3: Subtract 2x from both sides of the equation to isolate the x term.
9x + 6 - 2x = 2x + 13 - 2x
7x + 6 = 13
4: Subtract 6 from both sides of the equation.
7x + 6 - 6 = 13 - 6
7x = 7
5: Divide both sides of the equation by 7 to solve for x.
(7x) ÷ 7 = 7 ÷ 7
x = 1
Hence, x = 1 is the solution to the equation 3x + 2 = (2x + 13) ÷ 3.
For more such questions on equation's, click on:
https://brainly.com/question/17145398
#SPJ8
Find the integer that exceeds –5 by the same amount that 13 exceeds –1. \
Answers
Answer:
7
Step-by-step explanation:
13 exceeds - 1 by - 1 + 13 = 12, then
- 5 + 12 = 7
Answer:
Step-by-step explanation:
Answer:
7
Step-by-step explanation:
13 exceeds - 1 by - 1 + 13 = 12, then
- 5 + 12 = 7