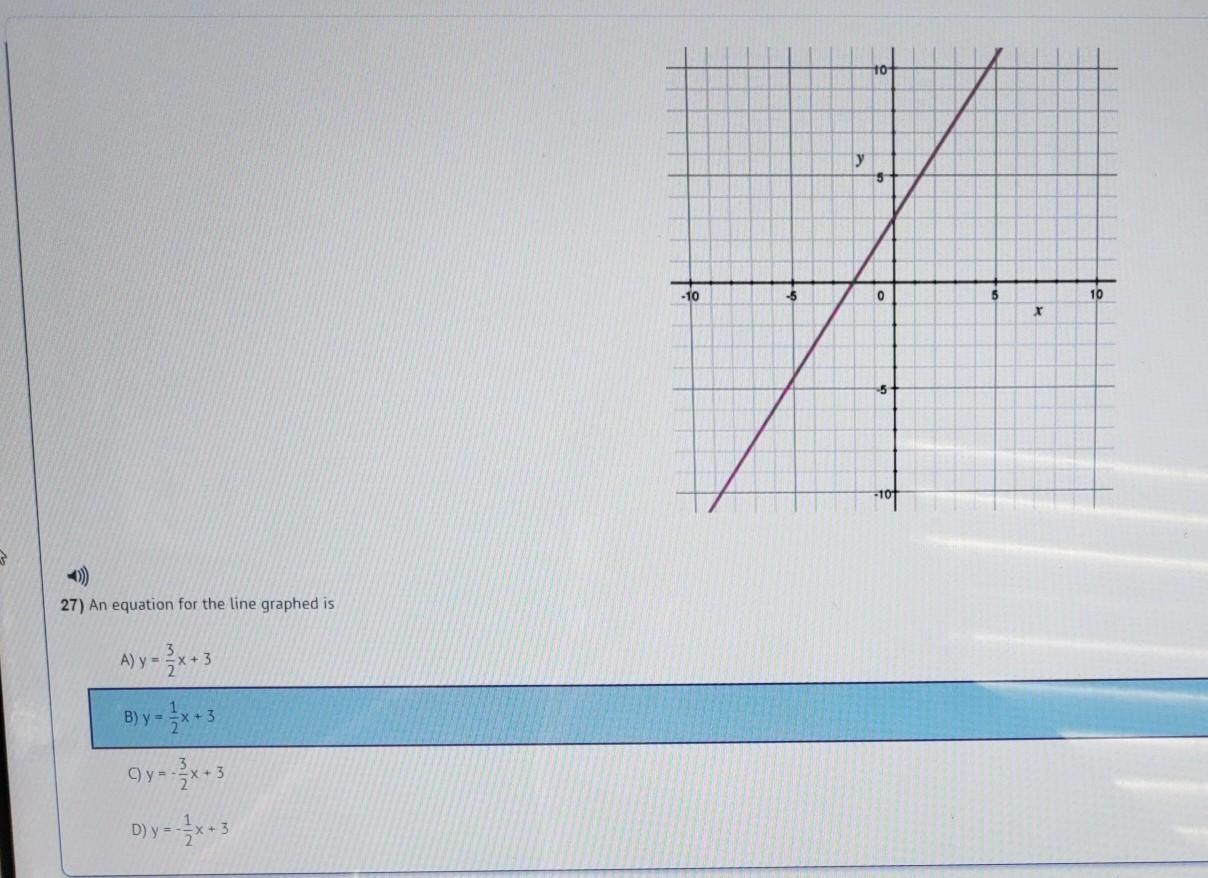
Answers
Answer:
the first option is correct
y= 3/2x + 3
Step-by-step explanation:
Related Questions
Find the solution set for this equation -n 2 + 8n=0
Answers
Answer:
0 and 8.
Step-by-step explanation:
n^2+8n=0
n(-n+8)=0
-n=-8 or n=8 and n=0.
Pls help evaluate the expression

Answers
Answer:
135
Step-by-step explanation:
3^3 = 27
27 x 10 / 2
270/2
135
Bethany has a photo website where she places photos that she has taken so others can see them. Below is how many likes each of her current photos were given: 10, 13, 15, 15, 17, 29 What is the average amount of likes each of her photos got? Hint: The average is your mean. 22 15 15.5 16.5
Answers
The average number of likes will be 16.5. the correct option is D.
What is a mean?Mean is defined as the ratio of the sum of the number of data sets to the total number of data. The mean is calculated by adding all the data points and dividing it by the total number of the data.
Given that Bethany has a photo website where she places photos that she has taken so others can see them. Below is how many likes each of her current photos was given: 10, 13, 15, 15, 17, 29.
The average will be calculated as:-
Mean = ( 10 + 13 + 15 + 15 + 17 + 29 ) / 6
Mean = 99 / 6
Mean = 16.5
Therefore, the average number of likes will be 16.5. the correct option is D.
To know more about mean follow
https://brainly.com/question/968894
#SPJ1
Find the area of the composite figure.
First, find the area of the triangle.
Triangle
Area = [?] cm2
...
Rectangle
Area = [ ]cm2
10 cm
30 cm
Total Area of Composite
Figure = [ ]cm2
16 cm
Answers
Answer:
209
Step-by-step explanation:
now if this is correct or not but i triedi hope this helps but dont trust me i dnt ko
in a class 4 by 5 of student are girls then find the number of boys
Answers
Step-by-step explanation:
Let the total number of boys be x.
We know that :-
\( \frac{1}{1} = 1\)
is the greatest fraction.
Now, considering the class AS whole, we can say that the value of class is 1.
According to Equation given:-
\( \dfrac{4}{5} + x = 1\)
\(x = \dfrac{1}{1} - \dfrac{4}{5} \)
Taking LCM,
\( \dfrac{5 - 4}{5} \)
\( = \dfrac{1}{5} \)
Fraction of the class are boys.
Hope it helps :D
Find the perimeter of the figure below, in feet.(Note: diagram is NOT to scale)

Answers
Question 1 of 10 Solve - 5 < 4x + 3 <= 7 x > - 2orx <= 1 B. x < - 2orx < 4 O C.-2 and x <= 1 D. x > 2 and x < 4
Answers
For the inequality -5 < 4x + 3 ≤ 7 the combined solution are x < -2 and x ≤ 1.
To solve the inequality -5 < 4x + 3 ≤ 7, we need to consider two separate inequalities:
Solve the inequality -5 < 4x + 3:
-5 < 4x + 3
Subtract 3 from both sides:
-5 - 3 < 4x
-8 < 4x
Divide both sides by 4
-8/4 > x
-2 > x
x < -2.
Now let's solve the inequality 4x + 3 ≤ 7:
4x + 3 ≤ 7
Subtract 3 from both sides:
4x ≤ 7 - 3
4x ≤ 4
Divide both sides by 4:
x ≤ 1
Therefore, the combined solution is x < -2 and x ≤ 1.
To learn more on Inequality click:
https://brainly.com/question/28823603
#SPJ1
Solve the quadratic equation 3x²+2x-4=0
Answers
Auuuu.........
...
.
.
.
.
.


A soccer ball travels upward from a height of 11 feet with an initial velocity of 20
feet per second. The quadratic function h (t) = -16t² + 20t+11 models the height
of the ball, where h (t) is the height, in feet, of the soccer ball and t is the time that
ball has been in the air, in seconds. When is the soccer ball above 15 feet?
A. The soccer ball is above 15 feet between 0 seconds and 0.5 second.
B. The soccer ball is above 15 feet between 0.5 second and 1 second.
C. The soccer ball is above 15 feet between 0:25 second and 1
second.
D. The soccer ball is above 15 feet between 0 seconds and 0.25 second.
Answers
The soccer ball is above 15 feet between 0.25 seconds and 1 second.
To determine when the soccer ball is above 15 feet, we need to find the values of t that satisfy the inequality h(t) > 15.
Given the quadratic function h(t) = -16t² + 20t + 11, we can rewrite the inequality as follows:
-16t² + 20t + 11 > 15
Subtracting 15 from both sides:
-16t² + 20t - 4 > 0
Simplifying further:
-16t² + 20t - 4 = -4(4t² - 5t + 1) = -4(t - 1)(4t - 1) > 0
Now, we can solve for t by finding the values that make the inequality true. We have two factors: (t - 1) and (4t - 1).
Setting each factor greater than zero and solving for t:
t - 1 > 0 => t > 1
4t - 1 > 0 => 4t > 1 => t > 1/4
So, we have t > 1 and t > 1/4. To satisfy both conditions, t must be greater than the maximum of 1 and 1/4, which is 1.
Therefore, the soccer ball is above 15 feet for t > 1 second.
The correct answer is:
C. The soccer ball is above 15 feet between 0.25 seconds and 1 second.
For such more questions on Soccer Ball Above 15ft
https://brainly.com/question/28374181
#SPJ8
ITS A SIMPLE 50 POINT QUESTION! PLEASE HELP!
is y = 4 a relation?
Answers
Answer:
Y=4 is a function
Step-by-step explanation:
And to me function is relation
Hope i got this right and have a great day :)
Answer: Yes
Step-by-step explanation:
Yes, y = 4, which is often written as f(x) = 4, is a function that means “take any input, and no matter what it is, produce an output of 4”.
SECTION 2-4
Convert hex number 743
to its decimal equivalent.
Answers
743₁₆ = 7 • 16² + 4 • 16¹ + 3 • 16⁰
743₁₆ = 1792 + 64 + 3
743₁₆ = 1859
Solve |x-5| > -2. Write your solution in interval notation.
Answers
Answer:
(−∞,∞)
Step-by-step explanation:
Since |x−5| is always positive and −2 is negative, |x−5| is always greater than −2, so the inequality is always true.
All real numbers
So, the answer is (−∞,∞)
What is the x-intercept of the line illustrated in the graph below? (Enter your answer as a number. If necessary, round to the nearest tenth.)
The line passes through the horizontal axis 2.5 units to the left of the origin. It passes through the vertical axis 1 unit above the origin.
Answers
Using the point-slope form of the equation of a line. the x-intercept of the line is \(-2.5\).
What is the intercept of the line?To find the x-intercept of the line, we need to find the point where the line intersects the x-axis. We know that the y-coordinate of this point is zero, because it is on the x-axis. Let's call the x-coordinate of this point "x".
We also know that the line passes through the point (-2.5,0), because it is 2.5 units to the left of the origin. Using the point-slope form of the equation of a line, we can write the equation of the line as:
\(y - 0 = m(x - (-2.5))\)
where m is the slope of the line. To find the slope, we can use the fact that the line passes through the point \((0,1)\) and \((-2.5,0)\):
\(m = (1 - 0) / (0 - (-2.5)) = 1 / 2.5 = 0.4\)
Substituting this into the equation of the line, we get:
\(y = 0.4(x + 2.5)\)
To find the x-intercept, we set y to zero and solve for x:
\(0 = 0.4(x + 2.5)\)
\(-2.5 = x\)
Therefore, the x-intercept of the line is \(-2.5.\)
Learn more about intercept here:
https://brainly.com/question/14180189
#SPJ1
Butternut is a ski resort in Massachusetts. One of their triple chair lifts unloads 5583 skiers per hour at the top of the slope. (A triple chair lift can carry three passengers per chair.) The ride from the bottom to the top takes 5 minutes. How many skiers are riding on the lift at any one time
Answers
Answer:
465.25 skiers at any one time.
Step-by-step explanation:
Given that:
Number of skiers unloaded per hour = 5583
Time taken to move from bottom to top = 5 minutes ;
Number of travels(rides) per hour :
1 hour / 5 minutes = 60 minutes / 5 minutes = 12 rides
If equal number of riders are conveyed per ride ; the Number of riders at any one time is :
Total number of riders conveyed at any one time = 5583 / 12
= 465.25 skiers per trip
X
The sum of Rosemary's age and Hannah's age is 102 years.
The difference between Rosemary's age and Hannah's age is 52 years.
Rosemary is older than Hannah.
Find the age of each woman by using simultaneous equations.
Steps to solve
Answers
Answer:
102 -52 =50 the age is 50 ufdhdgrthui
Let Rosemary's age = X
and Hannah's age = Y
According to question,
X + Y = 102 … (i)
X - Y = 52 … (ii)
Adding the equation (i) + (ii)
We get,
2X = 154
X = 77
now putting the value of X in Equation (ii)
We get,
77 - Y = 52
Y = 77-52
Y = 25
Hence, Rosemary's age =77 and Hannah's age = 25
Which equation finds the length of side c of this right triangle
Answers
Answer:
Find The Length Of The Side Of A Right Triangle : Example Question #1. Explanation: The Pythagorean Theorem gives us a2 + b2 = c2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides.
Step-by-step explanation:
Answer:
see below
Step-by-step explanation:
Use the Pythagorean Theorem to find c:
a² + b² = c²
√a² + b² = √c²
c = √a² +b²
Determine how long it will take for a principal amount of $1,500 to become double its initial value when deposited into an account paying interest at a rate of 13%, continuously compounded.
A.
5.33 years
B.
6.32 years
C.
11.25 years
D.
14.33 years
c is incorrect
Answers
you roll a standard cube. find p(number greater than 3)
Answers
The probability of rolling a number greater than 3 is 1/2 or 0.5.
When rolling a standard cube, there are six possible outcomes, corresponding to the six faces of the cube. Each face has a number from 1 to 6.
To find the probability of rolling a number greater than 3, we need to determine the number of favorable outcomes (rolling a number greater than 3) and divide it by the total number of possible outcomes (rolling any number from 1 to 6).
The favorable outcomes for rolling a number greater than 3 are: 4, 5, and 6. So, there are three favorable outcomes.
The total number of possible outcomes is six since there are six faces of the cube.
Therefore, the probability of rolling a number greater than 3 is:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 3 / 6
Probability = 1/2
Hence, the probability of rolling a number greater than 3 is 1/2 or 0.5.
for such more question on probability
https://brainly.com/question/23417919
#SPJ8
How can you get 3/3 -1/6?
Answers
9514 1404 393
Answer:
5/6
Step-by-step explanation:
Addition or subtraction of fractions requires a common denominator. The value 3/3 can be multiplied by 2/2 to give 6/6, which has the same denominator as the other fraction.
\(\dfrac{3}{3}-\dfrac{1}{6}=\dfrac{3\cdot2}{3\cdot2}-\dfrac{1}{6}\\\\=\dfrac{6}{6}-\dfrac{1}{6}=\dfrac{6-1}{6}=\boxed{\dfrac{5}{6}}\)
Complete the equation of the line through (-10,3 and (-8,-8)
Answers
Answer:
y=-5.5x-52
Step-by-step explanation:
Your input: find the equation of a line given two points P = (-10 , 3) and Q = (-8 , -8). The slope of a line passing through the two pointsP=(x1,y1) and Q=(x2,y2) is given byWe have that x1 = -10 , y1 = 3, x2 = -8 , y2 = -8Step 2:Plug the given values into the formula for slope:Step 3:Now, the y-intercept is b=y1−m⋅x1 (or b=y2−m⋅x2, the result is the same).b = 3 - (-5.5) ⋅ (-10) = -52Step 4:Finally, the equation of the line can be written in the form y=mx+b.y = -5.5x -52The equation of the line in the slope-intercept form is:y = -5.5x -52The equation of the line in the point-slope form is:y - (3) = -5.5 ⋅ ( x - (-10))The equation of the line in the point-slope form is:y - (-8) = -5.5 ⋅ ( x - (-8))The general equation of the line is:-5.5x - y -52 = 0
What is the product of the polynomials below?
(7x2+2x+4)(2x+5)
Answers
Answer:
This is a simple multiplication problem.
Here is my steps:
(14x^3 + 35x^2 + 4x + 10x + 8x + 20)
Combine like terms:
(14x^3 + 35x^2 + 22x + 20)
And that is your answer^^
Answer:
14x3+ 39x2 +8x +20
Step-by-step explanation:
Use the distributive property and/or the FOIL (front, outer, inner, last) method.
First:
Multiply (7x2)(2x)
=14x3
Then (7x) (5)
=35x2
Second:
Multiply (2x)(2x)
=4x2
Then (2x)(5)
=10
Third:
Multiply 4(2x)
=8x
Then (4)(5)
=20
You should get:
14x3 +35x2 +4x2 +10 +8x +10
Add all common numbers.
You should get:
14x3+ 39x2 +8x +20
A
B
C
D
37. What is the length of side P in the figure below?
6.7 cm
11 cm
15 cm
45 cm
20 cm
25 cm
P

Answers
The length of the side P is 15 cm. And the right option is C.
What is Pythagoras theorem?Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
To calculate the length of side P we use Pythagoras theorem's formula
Pythagoras formula:
a² = b²+c²......................... Equation 1Where:
a = Diagonal of the rectangleb = Length of the rectanglec = Width of the rectangleFrom the diagram,
Given:
a = 25 cmb = 20 cmc = p cmSubstitute these values into equation 1
25² = 20²+p²p² = 25²-20²p² = 225p = √225p = 15 cmHence, the right option is C 15 cm.
Learn more about Pythagoras theorem here: https://brainly.com/question/27997683
#SPJ1
Can anyone help please. Please show work too

Answers
The solutions to the system of equations are x = 2 and 4
How to determine the solution to the system of equationsFrom the question, we have the following parameters that can be used in our computation:
f(x) = x - 3
g(x) = 1/(x - 3)
The solution to the system of equations implies that
f(x) = g(x)
So, we have
x - 3 = 1/(x - 3)
Cross multiply the equation
This gives
(x - 3)² = 1
So, we have
x - 3 = ±1
Add 3 to both sides
x = 3 ± 1
So, we have
x = 2 and 4
Hence, the solutions to the system of equations are x = 2 and 4
Read more about equations at
https://brainly.com/question/148035
#SPJ1
2.write the equation of a circle with the following parameters

Answers
Solution:
Given the center O(h,k), of a circle and a point A(a,b), it is passing through.
The distance from the center to the circumference is called the radius, r. Thus;
\(\begin{gathered} O(0,-1),A(\sqrt{35},0) \\ \\ |OA|=r=\sqrt{(0-(-1))^2+(\sqrt{35}-0)^2} \\ \\ r=\sqrt{1+35} \\ \\ r=6 \\ \end{gathered}\)Since the equation of a circle is;
\((x-h)^2+(y-k)^2=r^2\)The, the equation of the circle is;
\(\begin{gathered} (h,k)=(0,-1) \\ \\ (x-0)^2+(y-(-1))^2=6^2 \\ \\ x^2+(y+1)^2=36 \end{gathered}\)ANSWER:
\(x^{2}+(y+1)^{2}=36\)As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
College Level Trigonometry any help will be appreciated

Answers
The angle between the beam and the 35 ft cable is 43 degrees
How to determine the angleTo determine the angle between the beam, we need to know all the trigonometric identities as well as their ratios.
We have the identities as;
secanttangentcosinecosecantcotangentsineAlso, their ratios are represented as;
sin θ = opposite/hypotenuse
cos θ = adjacent/hypotenuse
tan θ = opposite/adjacent
From the information given, we have that;
sin θ = 65/95
divide the values
sin θ = 0. 6842
find the inverse
θ = 43 degrees
Learn about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
Suppose that y varies directly with x, and y= --27 when x= --3 .
A) write a direction variation equation that relates x and y.
B) Find Y when x= 5
Answers
Answer:
A) y=9x
B) y=45 when x=5
Step-by-step explanation:
Part A
\(y=kx\\-27=k(-3)\\-27=-3k\\9=k\\y=9x\)
Part B
\(y=9(5)\\y=45\)
Find the stable distribution for the regular stochastic matrix.
matrix [0.4 0.2
0.6. 0.8
Answers
the stable distribution for the given regular stochastic matrix is approximately:
π ≈ [0.5455, 0.2404, 0.2141]
How to solve?
To find the stable distribution for the regular stochastic matrix, we need to solve the equation:
πA = π
where π is the stable distribution and A is the transition matrix.
The given matrix is:
[0.4 0.2 0.6]
[0.8 0 0.2]
[0.1 0.9 0 ]
We can set up the equation as:
π[0.4 0.2 0.6] = π
π[0.8 0 0.2] π
π[0.1 0.9 0 ] π
Expanding this equation, we get:
π₁(0.4) + π₂(0.8) + π₃(0.1) = π₁
π₁(0.2) + π₃(0.9) = π₂
π₁(0.6) + π₂(0.2) = π₃
π₁ + π₂ + π₃ = 1
Simplifying and rearranging, we get:
0.4π₁ - 0.8π₂ + 0.1π₃ = 0
-0.2π₁ + 0.9π₃ - π₂ = 0
0.6π₁ + 0.2π₃ - π₃ = 0
π₁ + π₂ + π₃ = 1
We can solve this system of equations using matrix methods, such as Gaussian elimination or inverse matrices. Solving the equations, we get:
π₁ ≈ 0.5455
π₂ ≈ 0.2404
π₃ ≈ 0.2141
Therefore, the stable distribution for the given regular stochastic matrix is approximately:
π ≈ [0.5455, 0.2404, 0.2141]
To know more about stochastic matrix related question visit:
https://brainly.com/question/29737056
#SPJ1
Los organizadores de la Feria de Alimentos colocan un contenedor de agua que mide 2,76 metros de largo, por 23,5 decímetros de ancho y por 196 centímetros de alto. ¿Cuál es el volumen del contenedor? Expresa la respuesta en metros cúbicos con aproximación a centésimos.
Answers
The volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
To find the volume of the container, we need to multiply its length, width, and height. Let's convert the given measurements to meters to ensure consistent units.
The length of the container is 2.76 meters.
The width of the container is 23.5 decimeters, which is equal to 2.35 meters (since 1 decimeter = 0.1 meters).
The height of the container is 196 centimeters, which is equal to 1.96 meters (since 1 meter = 100 centimeters).
Now we can calculate the volume of the container:
Volume = Length × Width × Height
Volume = 2.76 meters × 2.35 meters × 1.96 meters
Volume ≈ 12.9516 cubic meters (rounded to four decimal places)
Therefore, the volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
A factory is discharging pollution into a lake at the rate of r(t) tons per year given below, where t is the number of years that the factory has been in operation. Find the total amount of pollution discharged during the first 7 years of operation. (Round your answer to two decimal places.)
Answers
Answer:
The total amount of pollution discharged during the first 7 years of operation is 1.955 tons
Step-by-step explanation:
Given
\(r(t) = \frac{t}{t^2 + 1}\)
Required
The total amount in the first 7 years
This implies that:
\(r(t) = \frac{t}{t^2 + 1}; [0,7]\)
The total amount is calculated by integrating r(t) i.e.
\(v = \int\limits^a_b {r(t)} \, dt\)
So:
\(v = \int\limits^7_0 {\frac{t}{t^2 + 1}} \, dt\)
--------------------------------------------------------------
We have:
\(t^2 + 1\)
Differentiate
\(d(t^2 + 1) = 2t\)
Rewrite as:
\(2t = d(t^2 + 1)\)
Solve for t
\(t = \frac{1}{2}d(t^2 + 1)\)
---------------------------------------------------------------------------
So:
Make t the subject
\(v = \int\limits^7_0 {\frac{t}{t^2 + 1}} \, dt\)
\(v = \int\limits^7_0\frac{1}{2}* {\frac{d(t^2 + 1)}{t^2 + 1}} \, dt\)
\(v = \frac{1}{2}\int\limits^7_0 {\frac{d(t^2 + 1)}{t^2 + 1}} \, dt\)
Integrate
\(v = \frac{1}{2}\ln(t^2 +1)|\limits^7_0\)
Expand
\(v = \frac{1}{2}[\ln(7^2 +1) - \ln(0^2 +1)]\)
\(v = \frac{1}{2}[\ln(50) - \ln(1)]\)
\(v = \frac{1}{2}[3.91 - 0]\)
\(v = \frac{1}{2}[3.91]\)
\(v = 1.955\)