help me please!!!!!!!1111

The answer will be 0. 10 >  0. 01 . Option B

Given the values as;

Turn the values into proper fractions

a. 0. 10 = 10/ 100

Reduce to simpler terms

= 10/ 100

= 1/ 10

b. 0. 01 = 1/ 100

a = 1/ 100

b = 1/ 100

This means that both decimals are not of  equal proportion and thus a is greater than (>) b

Thus, the answer will be 0. 10 >  0. 01 . Option B

Learn more about decimals here:

https://brainly.com/question/1827193

#SPJ1

To construct a frequency histogram based on the given temperature data, we will use the temperature ranges as the x-axis and the number of days as the y-axis.

The temperature ranges and their corresponding frequencies are as follows:

30-39: 2 days

40-49: 26 days

50-59: 28 days

60-69: 8 days

70-79: 2 days

To create the histogram, we will represent each temperature range as a bar and the height of each bar will correspond to the frequency of days.

Using an appropriate scale, we can label the x-axis with the temperature ranges (30-39, 40-49, 50-59, 60-69, 70-79) and the y-axis with the frequency values.

Now, we can draw rectangles (bars) on the graph, with the base of each rectangle corresponding to the temperature range and the height representing the frequency of days. The height of each bar will be determined by the corresponding frequency value.

For such more question on frequency

https://brainly.com/question/254161

#SPJ8

Part (a)

The cost is the initial cost plus the cost per slushie multiplied by the number of slushies sold.

\(C(x)=500+1.25x\)

Part (b)

The revenue is the number of slushies sold multiplied by the amount charged per slushie.

\(R(x)=3.50x\)

Answer:

a

   The  percentage is

            \(P(x_1 < X < x_2 ) = 51.1 \%\)

b

   The probability is  \(P(Z > 2.5 ) = 0.0062097\)

Step-by-step explanation:

From the question we are told that

        The  population mean is  \(\mu = 800\)

        The  variance is  \(var(x) = 1600 \ kg\)

        The  range consider is  \(x_1 = 778 \ kg \ x_2 = 834 \ kg\)

         The  value consider in second question is  \(x = 900 \ kg\)

Generally the standard deviation is mathematically represented as

        \(\sigma = \sqrt{var (x)}\)

substituting value

        \(\sigma = \sqrt{1600}\)

       \(\sigma = 40\)

The percentage of a cucumber give the crop amount between 778 and 834 kg  is mathematically represented as

       \(P(x_1 < X < x_2 ) = P( \frac{x_1 - \mu }{\sigma} < \frac{X - \mu }{ \sigma } < \frac{x_2 - \mu }{\sigma } )\)

    Generally  \(\frac{X - \mu }{ \sigma } = Z (standardized \ value \ of \ X)\)

So

      \(P(x_1 < X < x_2 ) = P( \frac{778 - 800 }{40} < Z< \frac{834 - 800 }{40 } )\)

      \(P(x_1 < X < x_2 ) = P(z_2 < 0.85) - P(z_1 < -0.55)\)

From the z-table  the value for  \(P(z_1 < 0.85) = 0.80234\)

                                            and \(P(z_1 < -0.55) = 0.29116\)  

So

             \(P(x_1 < X < x_2 ) = 0.80234 - 0.29116\)

             \(P(x_1 < X < x_2 ) = 0.51118\)

The  percentage is

            \(P(x_1 < X < x_2 ) = 51.1 \%\)

The probability of cucumber give the crop exceed 900 kg is mathematically represented as

             \(P(X > x ) = P(\frac{X - \mu }{\sigma } > \frac{x - \mu }{\sigma } )\)

substituting values

             \(P(X > x ) = P( \frac{X - \mu }{\sigma } >\frac{900 - 800 }{40 } )\)

             \(P(X > x ) = P(Z >2.5 )\)

From the z-table  the value for  \(P(Z > 2.5 ) = 0.0062097\)

Answer:

x=5

Step-by-step explanation:

i think you posted this question twice, but here it is:

in order for this figure to truly be a kite, AD and AB have to be equal.

So:

4x=x+15

now we must solve the equation:

3x=15

x=5

We can reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the left foot is longer than the right foot.

A statistical test is required to determine whether the length of the left foot is greater than the length of the right foot. The null hypothesis states that there is no difference in average length between the left and right feet. The alternative hypothesis is that the left foot's average length is greater than the right foot's average length.

This hypothesis is one-tailed, as we are only interested in whether the left foot is longer than the right foot. We are not considering the possibility that the right foot could be longer than the left foot.

A t-test can be used to determine whether the difference in average length between the left and right feet is statistically significant. We can reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the left foot is longer than the right foot if the p-value of the t-test is less than the chosen significance level (e.g., 0.05).

Learn more about null hypothesis at https://brainly.com/question/25263462

#SPJ1

Answer: \(9\ ft/rad\)

Step-by-step explanation:

Given

Length of the ladder is \(l=18\ ft\)

Angle between the wall and the ladder is \(\theta\)

from the figure, we can write

\(\Rightarrow \sin \theta=\dfrac{x}{18}\\\\\Rightarrow x=18\sin \theta\)

Differentiate the above equation w.r.t \(\theta\)

\(\Rightarrow \dfrac{dx}{d\theta}=18\cos \theta\\\\\text{at }\theta=\dfrac{\pi }{3}\\\\\Rightarrow \dfrac{dx}{d\theta}=18\cos(\dfrac{\pi}{3})\\\\\Rightarrow \dfrac{dx}{d\theta}=18\times 0.5\\\\\Rightarrow \dfrac{dx}{d\theta}=9\ ft/rad\)

The equation that shows the point-slope form of the line passing through (3, 2) with a slope of (1/2) is:

y - 2 = (1/2)(x - 3)

In the point-slope form of a linear equation, the formula is y - y1 = m(x - x1), where (x1, y1) represents a point on the line, and m represents the slope of the line. By substituting the given values into the formula, we can determine the correct equation.

In this case, the given point is (3, 2) and the slope is (1/2). Plugging these values into the formula, we get:

y - 2 = (1/2)(x - 3)

This equation represents the line passing through the point (3, 2) with a slope of (1/2). It is in the point-slope form, which allows us to easily determine the equation of a line based on a given point and slope.

Therefore, the correct equation is y - 2 = (1/2)(x - 3).

For more such answers on Point slope

https://brainly.com/question/29797287

#SPJ8

Answer: B

Step-by-step explanation:

Answer:

8

Step-by-step explanation:

Answer:

0.125

Step-by-step explanation:

Answer:

Explanation:

Given

Using the identity:

Answer:

gₙ = gₙ₋₁ + 0.4, with g₁ = 6.4

Step-by-step explanation:

The n-th term of an arithmetic sequence can be written as:

gₙ = g₁ + (n - 1)*d

Where g₁ is the first value, and d is the difference between any two consecutive terms of this sequence.

Then we have the equations:

g₅ = 8 = g₁ + (5 -1)*d

g₁₀ = 10 = g₁ + (10 - 1)*d

This is a system of equations, we can rewrite this as:

8 = g₁ + 4*d

10 = g₁ + 9*d

To solve this, the first step will be isolate one of the variables in one of the equations, i will isolate g₁ in the first equation:

g₁ = 8 - 4*d

Now we can replace this in the second equation to get:

10 = 8 - 4*d + 9*d

10 = 8 + 5*d

10 - 8 = 5*d

2 = 5*d

2/5 = d = 0.4

Now with this, we can find the value of g₁ by using the equation:

g1 = 8 - 4*d = 8 - 4*(2/5) = 8 - 8/5 = 6.4

Then the nth term of this sequence can be written as:

gₙ = 6.4 + (n - 1)*0.4

This relation also can be written as:

gₙ = gₙ₋₁ + d = gₙ₋₁ + 0.4, with g₁ = 6.4

Then the correct option is the second option.

The remainder theorem indicates that remainder when the polynomial x⁵ - 3·x⁴ - 2·x³ - 5·x² + 5·x + 12 is divided by (x - 1) is 8

The remainder theorem specifies the relationship between the division of a polynomial by a linear factor to the value of the polynomial at a specified point

The remainder when the polynomial expression; x⁵ - 3·x⁴ - 2·x³ - 5·x² + 5·x + 12 is divided by x - 1, can be found using the remainder theorem by plugging in x = 1 in the function as follows;

f(1) = 1⁵ - 3 × 1⁴ - 2 × 1³ - 5 × 1² + 5 × 1 + 12 = 8

The remainder when x⁵ - 3·x⁴ - 2·x³ - 5·x² + 5·x + 12 is divided by (x - 1) therefore is 8

Learn more on the remainder theorem here: https://brainly.com/question/17256898

#SPJ1

A. Ram spent $18 on six pens and six books. The grand total is $72.

B. The cost of each pen is $9.

C. The variable is called x.

What is an equation?

A set of variables, constants, and mathematical operations such as addition, subtraction, multiplication, or division balanced by the equal sign is known as an equation. The equation's left-hand side (LHS) is on the left side, and its right-hand side (RHS) is on the right side (RHS).

Here, we have

Given: the equation 6x + 18 = 72:

A. The issue is that Ram spent $18 on six pens and six books. The total amount he paid is $72.

B. The following equation will be used to demonstrate this:

6x + 18 = 72

Compile similar terms.

6x = 72 - 18

6x = 54

On dividing,

x = 54 / 6.

x = $9

Hence, each pen will set you back $9.

C. The variable's value is x = 9.

Hence, the pen's price is 9.

To learn more about the equation from the given link

https://brainly.com/question/28405823

#SPJ1

Answer:

If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.

6(3x) = 4(4x + 1)

18x = 16x + 4

2x = 4

x = 2

Answer:

i think it 27. Am i right?

Step-by-step explanation:

The speed of the car is 108 kilometers per hour and the distance covered in 5 hours is 540 kilometers.

Speed is simply referred to as distance traveled per unit time.

It is expressed as;

Speed = Distance ÷ time.

Given that the car is traveling at a rate of 30 meters per second.

First, convert the car's speed from meters per second to kilometers per hour using the conversion factor.

1 kilometer = 1000 meters

1 hour = 3600 seconds

Hence;

Speed = 30m/s = ( 30 × 3600/1000 )kmh

Speed = 108 kmh

Next, the distance covered in 5 hours will be:

Speed = Distance / time

Distance = speed × time

Distance = 108 kmh × 5 h

Distance = 540 km

Therefore, the disatnce covered is 540 kilometers.

Learn more about speed here: brainly.com/question/7359669

#SPJ1

Answer:

Step-by-step explanation:

Answer:

8 km is equal to 800,000 cm

so 800,000/16,000 which is 50

Step-by-step explanation:

so the answer is 50 cm

Answer:

Brand A  Costs 37.38 per ounce and Brand B cost 31.19 per ounce hope this helped ^-^

Answer:

x = 1, y = 6

or

x = 5, y = 2.

Step-by-step explanation:

y=x2−7x+12

y=−x+7

Substitute for y in the first equation:

- x + 7 = x^2 - 7x + 12

x^2 - 7x + x + 12 - 7 = 0

x^2 - 6x + 5 = 0

(x - 1)(x - 5) = 0

x = 1, 5.

When x = 1, y = -1 + 7 = 6.

when x = 5, y = -5+7 = 2.

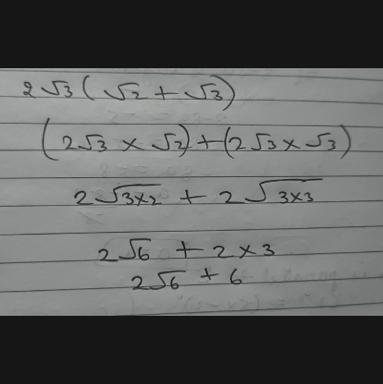
If you are dealt 4 cards from a shuffled deck of 52 cards, the probability of getting two queens and two kings is:  0.000133.

Number of ways to get two of the four queens = 4C2 = 6 ways

Number of ways to get  two of the four kings =  4C2 = 6 ways

Number of ways to get none of the deck = 48C0 = 1 way

Hence,

Number of  ways to get four cards  = 6 x 6 x 1

Number of  ways to get four cards  =  36 ways

Number of ways 4 cards can be chosen from 52 cards = 52C4 = 270725 ways

So,

Probability = 36 ways / 270725 ways

Probability = 0.0001329

Probability = 0.000133 (Approximately)

Therefore the probability is 0.000133.

Learn more about probability here: https://brainly.com/question/24756209

#SPJ1

Answer:

Please attach a photo to this so I can better answer your question

Answer:

54 x 1.4 = 54 x 140/100 = 75 60/100

75.6

Step-by-step explanation:

Answer:

44.8 square yards

Step-by-step explanation:

     a = 7.8 yds

     b = 5 yds

    h =  7 yds

    \(\sf \boxed{\bf Area \ of \ trapezoid = \dfrac{(a +b)*h}{2}}\)

Here, a and b are the parallel lines and h is the height between the parallel lines.

                                        \(\sf = \dfrac{(7.8+5)*7}{2}\\\\= \dfrac{12.8*7}{2}\\\\=6.4*7\\\\=44.8 \ square \ yards\)

Answer:

Vector is equal to vector b. For two vectors to be equal, they must have both the magnitude and the directions equal.

Step-by-step explanation:

Answer:

a) To solve the differential equation y''-2y'-3y= e^4x, we first find the characteristic equation:

r^2 - 2r - 3 = 0

Factoring, we get:

(r - 3)(r + 1) = 0

So the roots are r = 3 and r = -1.

The general solution to the homogeneous equation y'' - 2y' - 3y = 0 is:

y_h = c1e^3x + c2e^(-x)

To find the particular solution, we use the method of undetermined coefficients. Since e^4x is a solution to the homogeneous equation, we try a particular solution of the form:

y_p = Ae^4x

Taking the first and second derivatives of y_p, we get:

y_p' = 4Ae^4x

y_p'' = 16Ae^4x

Substituting these into the original differential equation, we get:

16Ae^4x - 8Ae^4x - 3Ae^4x = e^4x

Simplifying, we get:

5Ae^4x = e^4x

So:

A = 1/5

Therefore, the particular solution is:

y_p = (1/5)*e^4x

The general solution to the non-homogeneous equation is:

y = y_h + y_p

y = c1e^3x + c2e^(-x) + (1/5)*e^4x

b) To solve the differential equation y'' + y' - 2y = 3xe^x, we first find the characteristic equation:

r^2 + r - 2 = 0

Factoring, we get:

(r + 2)(r - 1) = 0

So the roots are r = -2 and r = 1.

The general solution to the homogeneous equation y'' + y' - 2y = 0 is:

y_h = c1e^(-2x) + c2e^x

To find the particular solution, we use the method of undetermined coefficients. Since 3xe^x is a solution to the homogeneous equation, we try a particular solution of the form:

y_p = (Ax + B)e^x

Taking the first and second derivatives of y_p, we get:

y_p' = Ae^x + (Ax + B)e^x

y_p'' = 2Ae^x + (Ax + B)e^x

Substituting these into the original differential equation, we get:

2Ae^x + (Ax + B)e^x + Ae^x + (Ax + B)e^x - 2(Ax + B)e^x = 3xe^x

Simplifying, we get:

3Ae^x = 3xe^x

So:

A = 1

Therefore, the particular solution is:

y_p = (x + B)e^x

Taking the derivative of y_p, we get:

y_p' = (x + 2 + B)e^x

Substituting back into the original differential equation, we get:

(x + 2 + B)e^x + (x + B)e^x - 2(x + B)e^x = 3xe^x

Simplifying, we get:

-xe^x - Be^x = 0

So:

B = -x

Therefore, the particular solution is:

y_p = xe^x

The general solution to the non-homogeneous equation is:

y = y_h + y_p

y = c1e^(-2x) + c2e^x + xe^x

c) To solve the differential equation y" - 9y' + 20y = x^2*e^4x, we first find the characteristic equation:

r^2 - 9r + 20 = 0

Factoring, we get:

(r - 5)(r - 4) = 0

So the roots are r = 5 and r = 4.

The general solution to the homogeneous equation y" - 9y' + 20y = 0 is:

y_h = c1e^4x + c2e^5x

To find the particular solution, we use the method of undetermined coefficients. Since x^2*e^4x is a solution to the homogeneous equation, we try a particular solution of the form:

y_p = (Ax^2 + Bx + C)e^4x

Taking the first and second derivatives of y_p, we get:

y_p' = (2Ax + B)e^4x + 4Axe^4x

y_p'' = 2Ae^4x +

Simply plug 3 into the equation.

\(f(3) = 3(3)^2+2(3) = 3(9) + 6 = 27 + 6 = 33\\\\\\f(3) = 33\)

Answer:

Step-by-step explanation:

Plugin x = 3 in the function

f(x) = 3x² + 2x

f(3) = 3*(3)² + 2*3               {3² = 3*3 = 9}

     = 3*9 + 6

     = 27 + 6

f(3) = 33