Answers
Answer:
The slope is 3To graph it you should put a point at any of the points that are in the table. Some easy ones are (0,0) and (2,6)Step-by-step explanation:
To find the slope you need to follow the formula shown below.
Slope (m) = ΔY/ΔX
Now solve
ΔY = 6 – 0 = 6
ΔX = 2 – 0 = 2
Write as a fraction
6/2
Convert to a number
6/2 = 3
And you have your slope. Now you just have to plot the points on the graph. As I said before, you can use any two points from the table.
Related Questions
fy
This graph shows a portion of an even function,
Use the graph to complete the table of values.
6
X
f(x)
-1
4
-3
-5
-6
2
DONE
2

Answers
Answer:
From top to bottom;
1,1,3,3
Step-by-step explanation:
mathematically, for an even function;
f(x) = f(-x)
what this mean is that;
f(-1) = f(1)
f(-3) = f(3)
f(-5) = f(5)
f(-6) = f(6)
so we have it that;
f(-1) = 1
f(-3) = 1
f(-5) = 3
f(-7) = 3
Choose the correct answer below for the following problem:
(‒489) + (‒764) =
A.
‒1,253
B.
275
C.
1,253
D.
‒275
Answers
Step-by-step explanation Answer:
A -1253
-489-764 = -1253
What is the measure of the angle?

Answers
Answer:
The angle of that is 90°
what decimal is equivalent to 4/40
Answers
Answer:10 percent
Step-by-step explanation:
divide the two
Convert the fraction to a decimal by dividing the numerator by the denominator.
0.1
Rewrite, using the distributive
property.
16b-8b = ([?]-8)b = [?]b
![Rewrite, using the distributiveproperty.16b-8b = ([?]-8)b = [?]b](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/9Tmzv11947B9UtnbF6DBvWJp63YQcon7.png)
Answers
Answer:
8b
Step-by-step explanation:
You can factor the b-term out since b-term exists for all terms in the expression. By factoring out, you are basically dividing the factored term off and put it outside of the bracket, thus:
\(\displaystyle{16b-8b=\left(16-8\right)b}\)
Then evaluate and simplify:
\(\displaystyle{\left(16-8\right)b=8\cdot b}\\\\\displaystyle{=8b}\)
solve 2x−3y=−1 , 3x+4y=24
Answers
Your answer should be x = 3
Plug the x value into one of the equations and you should get y = 7/3
The solution is (3, 7/3)
What is the product of d−9 and 2d2+11d−4 ?
Answers
The product of the terms \((d - 9)\) and \((2d^{2} + 11d -4)\) will be \((2d^{3} - 7d^{2} - 103d + 36)\).
We have to find the product of two terms.
First term = (d - 9)
Second term = \((2d^{2} + 11d -4)\)
To find the product of these two terms, we will be using the distributive property. According to the distributive property, when we multiply the sum of two or more addends by a number, it will give the same result as when we multiply each addend individually by the number and then add the products together.
We have to find : \((d - 9) (2d^2 + 11d -4)\)
Using the distributive property,
\(d * 2d^{2} + d * 11 + d * (-4) - 9 * 2d^2 - 9 * 11d - 9 * (-4)\)
After further multiplication, we get
\(2d^{3} + 11d^2 - 4d - 18d^{2} - 99d + 36\)
Now, combine all the like terms.
\(2d^{3} + 11d^{2} - 18d^{2} - 4d - 99d + 36\)
\(2d^{3} - 7d^{2} - 103d + 36\)
Therefore, the product of d-9 and 2d^2 + 11d -4 is \(2d^{3} - 7d^{2} - 103d + 36\)
To learn more about the product and distributive property;
https://brainly.com/question/2807928
#SPJ4
6. Find the distance between (-4, 5) and (7, 18).
O 15.96
16.08
O 16.23
O 17.03
Answers
Greetings from Brasil...
The expression that allows you to calculate the distance between two points is:
d(A; B) = √[(Xb - Xa)² + (Yb - Ya)²]d(A; B) = √[(7 - (- 4))² + (18 - 5)²]
d(A; B) = √[(7 + 4)² + 13²]
d(A; B) = √[11² + 13²]
d(A; B) = √[121 + 169]
d(A; B) = √290
d(A; B) ≈ 17.03
An experiment calls for each student to use 3.50g of sodium hydroxide. There is only 78.2g of sodium hydroxide remaining. How many students can complete the experiment?
Answers
John took all his money from his savings account. He spent $88 on a radio and 1/4 of what was left on presents for his friends. Of the money remaining, John put 4/11 into a checking account and the last remaining $420 was left to charity. How much money did John originally have in his savings account?
Answers
Answer:
$968
Step-by-step explanation:
x= the money John originally had in his savings account
The statement says that John spent $88 on a radio and 1/4 of what was left on presents for his friends. This means that the remaining money is 3/4 of the total amount minus the money spent on the radio:
3/4(x-88)
Then, it says that of the money remaining, John put 4/11 into a checking account and the last remaining $420 was left to charity. Since, he spent 4/11 of the remining 3/4(x-88), the remaining is 7/11 of that and that remaining is equal to $420 that was the money left at the end:
7/11(3/4(x-88))= 420
21/44(x-88)=420
21/44x-42=420
21/44x=462
x=968
According to this, the money that John originally had in his savings account was $968.
He spent $88 on a radio: 968-88= 880
1/4 of what was left on presents for his friends: 880/4= 220
880-220=660
Of the money remaining, John put 4/11 into a checking account: 660*(4/11)=240
the last remaining $420 was left to charity: 660-240= 420
if f(x) = x^2 - 4 and g (x) = x + 1 simplify the following
f( x ) + g( x ) =
f( x ) - g( x ) =
f( x ) / g( x ) =
f( x ) * g( x ) =
Answers
The values of functions are:
a) f( x ) + g( x ) = x² + x - 3
b) f( x ) - g( x ) = x² - x - 5
c) f( x ) / g( x ) = x² - 4/ (x+ 1)
d) f( x ) * g( x ) = x³ + x² - 4x - 4
what is function?In mathematics, a function is represented as a rule that produces a distinct result for each input x. In mathematics, a function is indicated by a mapping or transformation. Typically, these functions are identified by letters like f, g, and h. The collection of all the values that the function may input while it is defined is known as the domain. The entire set of values that the function's output can produce is referred to as the range. The set of values that could be a function's outputs is known as the co-domain.
Given:
f(x) = x² - 4 and g (x) = x + 1
a) f( x ) + g( x )
= x² - 4 + x+ 1
= x² + x - 3
b) f( x ) - g( x )
= x² - 4 - ( x+ 1)
= x² - 4 - x- 1
= x² - x - 5
c) f( x ) / g( x )
= x² - 4/ (x+ 1)
d) f( x ) × g( x )
= (x²- 4)( x+ 1)
= x³ + x² - 4x - 4
Learn more about function here:
https://brainly.com/question/12431044
#SPJ1
Any help? Much appreciated

Answers
Answer:
\(\frac{6+\sqrt{27} }{4-\sqrt{3} } = \frac{r+s\sqrt{3} }{13} \\We\ may\ multiply\ the\ numerator\ and\ denominator\ with\ (4+\sqrt{3} ).\\Hence,\\\frac{(6+\sqrt{27})(4+\sqrt{3}) }{13} = \frac{r+s\sqrt{3} }{13} \\Hence,\\24+6\sqrt{3} +4\sqrt{27} +9= r+s\sqrt{3}\\24+6\sqrt{3} +4*3\sqrt{3} } +9= r+s\sqrt{3}\\24+6\sqrt{3} +12\sqrt{3}+9 = r+s\sqrt{3}\\33+18\sqrt{3} = r+s\sqrt{3}\\Hence,\\r=33, s=18\)
Please help me with this.

Answers
Answer: 3
Step-by-step explanation:
i might be wrong
The graphs of f (x) and g (x) are shown below.

Answers
Answer:
B) (-∞, 2)
Step-by-step explanation:
Given functions:
\(f(x)=x-3\)
\(g(x)=-0.5x\)
To find the interval for which (f - g)(x) is negative, set (f - g)(x) less than zero and solve for x:
\(\begin{aligned}(f-g)(x)& < 0\\f(x)-g(x)& < 0\\(x-3)-(-0.5x)& < 0\\x-3+0.5x& < 0\\1.5x-3& < 0\\1.5x& < 3\\x& < 2\end{aligned}\)
Therefore, the interval for which the composite function (f - g)(x) is negative is:
(-∞, 2)Is it possible to prove that the triangles are congruent by using the AAS congruence theorem?
Answers
Yes, it is possible to prove that two triangles are congruent by using the AAS congruence theorem.
The AAS congruence theorem states that if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent. This theorem can be used to prove that two triangles are congruent if two of the angles in the triangle and the side between them are congruent to two angles and the side between them of the other triangle. To prove congruence using the AAS congruence theorem, it is important to use the right angle and side measurements to ensure that the two triangles are congruent. If the measurements are correct, then the two triangles will be congruent.
To learn more about the triangle, visit:
brainly.com/question/2773823
#SPJ4
Yes, it is possible to prove that two triangles are congruent by using the AAS congruence theorem.
The AAS congruence theorem
it states that if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent.
This theorem can be used to prove that two triangles are congruent if two of the angles in the triangle and the side between them are congruent to two angles and the side between them of the other triangle.
To prove congruence using the AAS congruence theorem, it is important to use the right angle and side measurements to ensure that the two triangles are congruent. If the measurements are correct, then the two triangles will be congruent.
Learn more about congruence here :_
https://brainly.com/question/7888063
#SPJ4
A tank of water in the shape of a cone is being filled with water at a rate of 12 m/sec. The base radius of the tank is 26 meters, and the height of the tank is 18 meters. At what rate is the depth of
Answers
The depth of the water in the cone-shaped tank is increasing at a rate of approximately 1.385 meters per second.
To determine the rate at which the depth of the water is changing, we can use related rates. Let's denote the depth of the water as h(t), where t represents time. We are given that dh/dt (the rate of change of h with respect to time) is 12 m/sec, and we want to find dh/dt when h = 18 meters.
To solve this problem, we can use the volume formula for a cone, which is V = (1/3)πr^2h, where r is the base radius and h is the depth of the water. We can differentiate this equation with respect to time t, keeping in mind that r is a constant (since the base radius does not change).
By differentiating the volume formula with respect to t, we get dV/dt = (1/3)πr^2(dh/dt). Now we can substitute the given values: dV/dt = 12 m/sec, r = 26 meters, and h = 18 meters.
Solving for dh/dt, we have (1/3)π(26^2) (dh/dt) = 12 m/sec. Rearranging this equation and solving for dh/dt, we find that dh/dt is approximately 1.385 meters per second. Therefore, the depth of the water in the tank is increasing at a rate of about 1.385 meters per second.
Learn more about volume of cone here: brainly.com/question/16419032
#SPJ11
Find the best linear approximation, L(x), to f(x) = e' near x = 0. i.L(x) = x+1 ii. L(x) = x iii. LX) = c + 1
Answers
The best linear approximation to the function f(x) = e^x near x = 0 is L(x) = x + 1.
The given function is f(x) = e^x near x = 0.
To find the best linear approximation, L(x), we use the formula:
L(x) = f(a) + f'(a)(x-a),
where a is the point near which we are approximating.
Let a = 0, so that a is near the point x = 0.
f(a) = f(0) = e^0 = 1
f'(x) = d/dx (e^x) = e^x;
so f'(a) = f'(0) = e^0 = 1
Substituting these values into the formula: L(x) = 1 + 1(x-0) = x + 1
Therefore, the best linear approximation to f(x) = e^x near x = 0 is L(x) = x + 1.
For instance, linear approximation is used to approximate the change in a physical quantity due to a small change in another quantity that affects it.
To know more about linear approximation, visit:
https://brainly.com/question/1621850
#SPJ11
What is the rate and unit rate of 175 miles in 4 hours
Answers
Answer: 43.75 (PLEASE GIVE BRAINLIEST)
Step-by-step explanation:
The rate can be calculated by dividing the distance traveled by the time it took to travel that distance. So, the rate for 175 miles in 4 hours is 175/4 = 43.75 miles per hour.
The unit rate, also known as the speed, is the rate per one unit of time, in this case one hour. So, the unit rate for 175 miles in 4 hours is 43.75 miles per hour.
Mr. A sold his land to Mr.B at a profit of 10%. Mr.B. sold it to Mr.C at a gain of 5%. Mr.C.paid N1240 more for the house than Mr. A paid. What did Mr. A paid.
Answers
Answer:
Mr. A initially paid approximately N8000 for the land.
Step-by-step explanation:
Step 1: Let's assume Mr. A initially purchased the land for a certain amount, which we'll call "x" in currency units.
Step 2: Mr. A sold the land to Mr. B at a profit of 10%. This means Mr. A sold the land for 110% of the amount he paid (1 + 10/100 = 1.10). Therefore, Mr. A received 1.10x currency units from Mr. B.
Step 3: Mr. B sold the land to Mr. C at a gain of 5%. This means Mr. B sold the land for 105% of the amount he paid (1 + 5/100 = 1.05). Therefore, Mr. B received 1.05 * (1.10x) currency units from Mr. C.
Step 4: According to the given information, Mr. C paid N1240 more for the land than Mr. A paid. This means the difference between what Mr. C paid and what Mr. A paid is N1240. So we have the equation: 1.05 * (1.10x) - x = N1240
Step 5: Simplifying the equation: 1.155x - x = N1240
Step 6: Solving for x: 0.155x = N1240
x = N1240 / 0.155
x ≈ N8000
Therefore, in conclusion, Mr. A initially paid approximately N8000 for the land.
Some doctors recommend that men drink 3 liters of water every day. There are approximately 29.6 milliliters in 1 fluid ounce. Which measurement is closest to the number of fluid ounces in 3 liters?
Answers
Combine like terms.
3p2q2-3p2q3+4p2q3-3p2q2+pq
Answers
Answer:
104
Step-by-step explanation:
:D
Suppose a golf club company has designed a new club, which it claims will allow a professional golfer to make a hole in 120% of the time and an amateur golfer 10% of the time. Professional an amateur golfers sign up to play 5 games of 18 holes each
Answers
A professional golfer to make about 40.7 holes over 5 rounds of golf with the new club, while an amateur golfer would only make about 1.6.
First, let's define some variables to represent the probabilities of making a hole for a professional golfer and an amateur golfer:
Let p be the probability that a professional golfer makes a hole with the new club.
Let q be the probability that an amateur golfer makes a hole with the new club.
According to the company's claims, we know that:
p = 1.2q (since the professional golfer makes a hole 120% of the time, which is 1.2 times the probability of the amateur golfer making a hole)
Next, we need to determine the probability of each golfer making a hole during one round of golf, which consists of 18 holes. Let's assume that each hole is independent of the others, meaning that the outcome of one hole does not affect the outcome of another. In that case, the probability of making at least one hole in a round can be calculated using the complement rule:
The probability that a professional golfer makes at least one hole in a round is 1 minus the probability that the golfer misses every hole: \(1 - (1-p)^{18} .\)
The probability that an amateur golfer makes at least one hole in a round is\(1 - (1-q)^{18} .\)
Now, let's use these probabilities to calculate the expected number of holes each golfer will make in 5 rounds of golf:
The expected number of holes made by a professional golfer in 5 rounds is 5 times the expected number of holes made in one round, which is \((1 - (1-p)^{18} )\times18.\)
The expected number of holes made by an amateur golfer in 5 rounds is 5 times the expected number of holes made in one round, which is \((1 - (1-q)^{18} )\times18.\)
We can simplify these expressions using the relationship between p and q:
The expected number of holes made by a professional golfer in 5 rounds is \(518(1 - (1-1.2q)^{18} ).\)
The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-q)^{18} ).\)
We can now evaluate these expressions using the values of p and q:
\(p = 1.2q, so q = p/1.2\)
Substituting this into the expressions above, we get:
The expected number of holes made by a professional golfer in 5 rounds is\(518(1 - (1-1.2(p/1.2))^{18} ) = 518(1 - (1-p)^{18} ).\)
The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-p/1.2)^{18} ).\)
Finally, we can evaluate these expressions using the given probabilities:
The expected number of holes made by a professional golfer in 5 rounds is\(518(1 - (1-1.2q)^{18} ) = 518(1 - (1-1.2(0.1))^{18} ) = 40.7.\)
The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-q)^{18} ) = 518(1 - (1-0.1/1.2)^{18} ) = 1.6.\)
So according to these calculations, we would expect a professional golfer to make about 40.7 holes over 5 rounds of golf with the new club, while an amateur golfer would only make about 1.6
for such more question on probability
https://brainly.com/question/24756209
#SPJ4
1. Find the area of each sector. Give your answer in two forms. 1) in terms of it and 2) using 3.14 for it.
Round all answers to the nearest tenth.

Answers
Answer:
1.
1) The area of the sector is 168.8π mi²
2) The area of the sector is 529.9 mi²
2.
1) The area of the sector is 42.3π in²
2) The area of the sector is 132.7 in²
Step-by-step explanation:
The formula of the area of a sector in a circle is A = \(\frac{x}{360}\) × π r², where
x is the central angle subtended by the arc of the sectorr is the radius of the circle1.
∵ The central angle subtended by the arc of the circle is 270°
∴ x = 270°
∵ The radius of the circle is 15 mi.
∴ r = 15
→ Substitute them in the formula of the area above
∵ A = \(\frac{270}{360}\) × π (15)²
∴ A = 168.75π mi²
→ Round it to the nearest tenth
∴ A = 168.8π mi²
1) The area of the sector is 168.8π mi²
∵ π = 3.14
∴ A = 168.75 × 3.14
∴ A = 529.875 mi²
→ Round it to the nearest tenth
∴ A = 529.9 mi²
2) The area of the sector is 529.9 mi²
2.
∵ The central angle subtended by the arc of the circle is 90°
∴ x = 90°
∵ The radius of the circle is 13 in
∴ r = 13
→ Substitute them in the formula of the area above
∵ A = \(\frac{90}{360}\) × π (13)²
∴ A = 42.25π in²
→ Round it to the nearest tenth
∴ A = 42.3π in²
1) The area of the sector is 42.3π in²
∵ π = 3.14
∴ A = 42.25 × 3.14
∴ A = 132.665 in²
→ Round it to the nearest tenth
∴ A = 132.7 in²
2) The area of the sector is 132.7 in²
please find the value for x

Answers
Answer:
x= 11
Step-by-step explanation:
Answer:
hope this answer will help you.

please help with my math
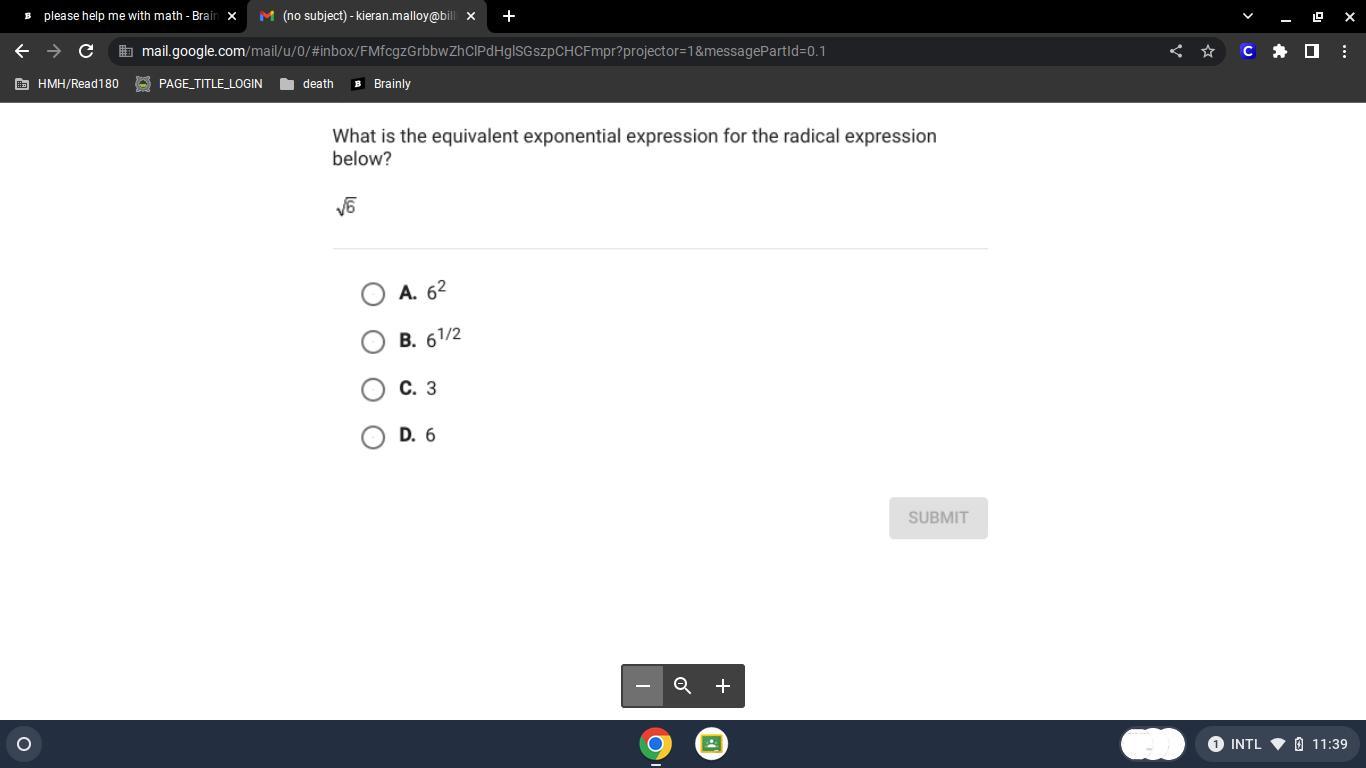
Answers
Answer:
B.) \(6^{\frac{1}{2}}\)
Step-by-step explanation:
Use the exponent rule that states \(a^{\frac{1}{m}}=\sqrt[m]{a}\). For this problem, let
a=6
m=2
So,
\(\sqrt6=6^{\frac{1}{2}}\)
as the spacing between joists increases, the maximum span for any board size: A. increases only. B. decreases only. C. increases and then decreases. D. decreases and than increases
Answers
As the spacing between joists increases, the maximum span for any board size will B. decrease only. This is because the wider the spacing between joists, the more weight and pressure will be placed on the boards that are spanning the gap between them.
This means that the boards will need to be stronger in order to support the weight without bending or breaking.
If the boards are not strong enough, they may sag or bow under the weight, which can create safety hazards or damage to the structure. Therefore, it is important to use the appropriate board size and spacing between joists for any given application in order to ensure structural integrity and safety.
In summary, increasing the spacing between joists will result in a decrease in the maximum span for any board size, as the boards will need to be stronger in order to support the weight and pressure. It is important to choose the right board size and joist spacing to maintain the structural integrity and safety of the building or structure.
To learn more about joists, refer:-
https://brainly.com/question/1927626
#SPJ11
Whats the answer for the whole problem please help i give brainliest.


Answers
Answer:
The equation for this is G= -3/2x + 12
and the interpretation of the context, I may get this wrong, is the Y-intercept is the number of gallons used per mile
Step-by-step explanation:
to find out the slope, you get the point from the y-intercept (0, 12) and you see how much you go down for the first number, then you see how much you go right for the second number until you reach the next point in which case it's (2, 9), which will give you 3 for the first number and 2 for the second number.
Then you place the first number above the second number and put a negative sign in front of the whole thing if the line is going down. So the number would be 3/2 and the line is going down, so the answer would be -3/2
to find the y-intercept, you just look at where the point starts on the y-intercept, which is at 12. So the y-intercept is 12.
Please help I need help with this badly asap !

Answers
Answer:
The third option
Step-by-step explanation:
It perfectly represents -24/3.
Answer this question plz thanks

Answers
Answer:
Option AStep-by-step explanation:
The area outside of the semicircle is the difference of the areas of the rectangle and the semicircle.
Area of rectangle:
A₁ = w(w + 5) = w² + 5wArea of the semicircle:
A₂ = 1/2*πd²/4 = 1/8*πw²The area we are looking for is:
A = A₁ - A₂A = w² + 5w - 1/8πw²Correct choice is A
According to the census, the median household income in Atlanta (1.5 Million households) was $52,000 in 1999. In June 2003, a market research organization takes a simple random sample of 750 households in Atlanta; 56% of the sample households had incomes over $52,000. Did median household income in Atlanta increase over the period 1999 to 2003?
a.) Formulate null and alternative hypotheses in terms of a box model.
b.) Calculate the appropriate test statistic and P.
c.) Did median family income go up?
Answers
a) The null hypothesis (H0) in this case would be that the median household income in Atlanta did not change between 1999 and 2003. The alternative hypothesis (Ha) would be that the median household income in Atlanta increased over the same period.
b) To test this, we can use a box model. The box represents the distribution of incomes in 1999, and the alternative hypothesis suggests that the median income in 2003 shifted to the right. We can calculate the z-score for the sample proportion (56%) using the formula z = (p - P0) / sqrt(P0(1-P0)/n), where p is the sample proportion, P0 is the hypothesized population proportion (52%), and n is the sample size. This will give us the test statistic.
To calculate the p-value, we can use the standard normal distribution table or a calculator to find the area under the curve beyond the test statistic. The p-value represents the probability of observing a sample proportion as extreme as the one we found, assuming that the null hypothesis is true.
c) If the p-value is smaller than a pre-determined significance level (e.g., 0.05), we would reject the null hypothesis. This would suggest that there is sufficient evidence to conclude that the median household income in Atlanta did increase between 1999 and 2003. If the p-value is larger than the significance level, we would fail to reject the null hypothesis and would not have enough evidence to conclude that the median household income increased.
To Know more about median household income in Atlanta Visit:
https://brainly.com/question/14087447
#SPJ11
