Answers
The interquartile range of the given box plot is 8. Therefore, the correct option is B.
From the given box plot,
Minimum value = 2
Maximum value = 19
First quartile = 6
Median = 8
Third quartile = 14
Interquartile range = 14-6
= 8
Therefore, the correct option is B.
Learn more about the box plot here:
https://brainly.com/question/1523909.
#SPJ1
Related Questions
Determine the slope of the line.

Answers
Answer:
The slope of the line is \(\frac{1}{4}\)
Step-by-step explanation:
I will be using (-3,-4) and (1,-3)
m = \(\frac{y_2-y_1}{x_2-x_1}\) = \(\frac{-3-(-4)}{1-(-3)}\) = \(\frac{1}{4}\)
y - mx + b
y = \(\frac{1}{4}\)x + b
Hope this helps!
In this case the slope is 1/4
5. Identify each of the following as convex or concave polygons:

Answers
Answer:
A) convex B) convex C) concave D) concave
Step-by-step explanation:
concave means going in on itself and convex is going outwards.
Rewrite the function f(x) = -2(x+2)²-11 in the form f(x) = ax²+bx+c.
X
S

Answers
Answer:
\(\displaystyle{f(x)=-2x^2-8x-19}\)
Step-by-step explanation:
Given the vertex equation:
\(\displaystyle{f(x)=-2(x+2)^2-11}\)
First, apply the perfect square formula, expanding to standard form:
\(\displaystyle{f(x)=-2(x^2+4x+4)-11}\)
Expand -2 in:
\(\displaystyle{f(x)=-2x^2-8x-8-11}\)
Evaluate or simplify:
\(\displaystyle{f(x)=-2x^2-8x-19}\)
Hence,
\(\displaystyle{f(x)=-2x^2-8x-19}\)
Answer:
\(\huge\boxed{\sf f(x) = -2x\² - 8x - 19}\)
Step-by-step explanation:
Given function:f(x) = -2(x + 2)² - 11
Using formula: (a + b)² = a² + 2ab + b²f(x) = -2[(x)² + 2(x)(2) + (2)²] - 11
f(x) = -2(x² + 4x + 4) - 11
Distribute
f(x) = -2x² - 8x - 8 - 11
f(x) = -2x² - 8x - 19\(\rule[225]{225}{2}\)
Find the equation of the line that passes through the point (2,-5) and is perpendicular to the line y=1/5x-2
Answers
The equation of the line passing through the point (2,-5) and is perpendicular to the line y = x/5-2 is y = -5x+5
What is a equation of a line?The equation of line is an algebraic form of representing the set of points, which together form a line in a coordinate system.
Given that, a line is passing through the point (2,-5) and is perpendicular to the line y = x/5-2, we need to find the equation of the line,
Let the name of line asked be a, and given line be b,
The general equation of the line is :- y = mx + c, where m is the slope and c is the y-intercept,
Therefore, In the line b, the slope m = 1/5
We know that, the lines which are perpendicular have negative reciprocals of their slopes,
Therefore, the slope of the line a = -5
Therefore, the equation of the line a, with c :-
y = -5x + c
To find c, put x = 2, and y = -5
-5 = -5(2) + c
-5 = -10 + c
c = 5
Therefore, the equation of the line a is :-
y = -5x+5
Hence, the equation of the line passing through the point (2,-5) and is perpendicular to the line y = x/5-2 is y = -5x+5
Learn more about equations of lines, click;
https://brainly.com/question/21511618
#SPJ1
IF YOU HELP ILL GIVE YOU BRAINLY PLEASE!!

Answers
Answer:
part a:
x lengths = 6
unit lengths = 2
part b:
6x+2
Step-by-step explanation:
You add the like terms, in this case, there are 6 x, so we have 6x, and two 1s, so 1+1= 2, and since 6x and 2 are not like terms, we can't add them, making our answer 6x+2
Answer:
Im past this subject, so this is what I remember. There are six x lengths, and I believe there are 2 NOT 8 unit lengths. For B the answer is 6x+2. Dont worry about the Brainly.
Step-by-step explanation:
describe all solutions of ax0 in parametric vector form, where a is row equivalent to the given matrix. |1 -2 -8 3 | |0 1 2 -4| x=x3__+x4__ (Type an integer or fraction for each matrix element.)
Answers
The solutions of Ax=0 in parametric vector form:
\(x_2\left[\begin{array}{c}-3&1&0&0\\\\\end{array}\right] +x_3\left[\begin{array}{c}0&0&1&0\\\\\end{array}\right] +x_4\left[\begin{array}{c}4&0&0&1\\\\\end{array}\right]\)
we have a matrix where A is the row equivalent to that matrix:
\(\left[\begin{array}{cccc}1&3&0&-4\\2&6&0&-8\\\end{array}\right]\)
The given matrix can be written in an Augmented form as:
\(\left[\begin{array}{ccccc}1&3&0&-4&0\\2&6&0&-8&0\\\end{array}\right]\)
Row Reduced Echelon Form can be obtained using the following steps.
Interchanging the rows R₁ and R₂
.\(\left[\begin{array}{ccccc}2&6&0&-8&0\\1&3&0&-4&0\\\end{array}\right]\)
Applying the operation R₂-->2R₂-R₁, to make the second.
\(\left[\begin{array}{ccccc}2&6&0&-8&0\\1&3&0&-4&0\\\end{array}\right]\) R₂-->2R₂-R₁,
\(\left[\begin{array}{ccccc}2&6&0&-8&0\\0&0&0&0&0\\\end{array}\right]\)
Dividing the first row by 2 to generate 1 at the
\(\left[\begin{array}{ccccc}2&6&0&-8&0\\0&0&0&0&0\\\end{array}\right]\) R₁--->1/2R₁
\(\left[\begin{array}{ccccc}1&3&0&-4&0\\0&0&0&0&0\\\end{array}\right]\)
From here the following equation can be deducted:
x₁+3x₂-4x₄=0
Making the subject of the equation:
x₁=-3x₂+4x₄
Hence, the Ax=0 parametric vector form’s solutions can be written as:
\(X=\left[\begin{array}{c}-3x_2+4x_4&x_2&x_3&x_4\\\\\end{array}\right] \\\\\\=\left[\begin{array}{c}-3x_1&x_2&0&0\\\\\end{array}\right] +\left[\begin{array}{c}0&0&x_3&0\\\\\end{array}\right] +\left[\begin{array}{c}4x_4&0&0&x_4\\\\\end{array}\right] \\\\\\ =x_2\left[\begin{array}{c}-3&1&0&0\\\\\end{array}\right] +x_3\left[\begin{array}{c}0&0&1&0\\\\\end{array}\right] +x_4\left[\begin{array}{c}4&0&0&1\\\\\end{array}\right]\)
Numerical Result:
\(x_2\left[\begin{array}{c}-3&1&0&0\\\\\end{array}\right] +x_3\left[\begin{array}{c}0&0&1&0\\\\\end{array}\right] +x_4\left[\begin{array}{c}4&0&0&1\\\\\end{array}\right]\)
To know more about Parametric vector form:
https://brainly.com/question/18513819
#SPJ4
A quadratic function with zeroes 1 and -9
Answers
Answer:
(x-1)(x+9) or x^2 + 8x-9, if you simplify.
Step-by-step explanation:
Step-by-step explanation:
By Factor theorem, (x - 1) and (x + 9) are factors of the function.
=> (x - 1)(x + 9) = x² + 8x - 9 is one such function.
The area of a carpet is 36x -12 square inches. If the width of the carpet is 3x - 1 inch, what is the length?
Answers
Answer:
The length is (36x -12)/(3x - 1) inStep-by-step explanation:
Given data
Area A= \(36x -12 in^2\)
Width W= \(3x - 1 in\)
we know that the area A= length * width
i.e A= L*W
we can solve for the length by making it subject of the formula
L= A/W
L= \(\frac{36x -12}{3x - 1} in \\\\)
8. Find the endpoint of AB given the midpoint, M, and the other endpoint, A.
M(-5.5, 2), A(2.3,-4.6)
Answers
Answer: (-13.3, 8.6)
Step-by-step explanation:
First we want to identify which side of the graph A lands on compared to x. We see that A's X value is greater, meaning it is on the right side of M.
We can then start finding the opposite coordinate by finding the distance between the x and y values of A and M. We can do this By subtracting the M values from the A values:
\(x-distance = 2.3-(-5.5) = 7.8\\y-distance = -4.6 - 2 = -6.6\)
We then need to subtract these values from the M coordinate in order to find the coordinate B opposite of A:
\(B-xValue = -5.5 - 7.8 = -13.3\\B-yValue = 2 - (-6.6) = 8.6\)
From this, we can tell our coordinate B has the value: (-13.3, 8.6)
Hope this helps, if you need any clarification please let me know.
Step-by-step explanation:
given 2 points
A (xa, ya)
B (xb, yb)
their midpoint is
M ((xa + xb)/2, (ya + yb)/2)
in our case
A (2.3, - 4.6)
M(-5.5, 2)
so,
-5.5 = (2.3 + xb)/2
-11 = 2.3 + xb
xb = -13.3
2 = (-4.6 + yb)/2
4 = -4.6 + yb
yb = 8.6
so,
B = (-13.3, 8.6)
PLZ I NEED HELP AND I DON"T KNOW THE ANSWER!!

Answers
Answer:
Step-by-step explanation:
$ 3750 = truck rental; $125 per ton of sugar transported
C is cost; S is number of tons transported
Equation relating C to S would be a linear equation like y = mx + b
C = 125S + $3750
This equation would be graphed in the first quadrant only
you would start with your y-intercept at (0, 3750)
As x increases by 1, your y increases by 125 yielding these points:
(1, 3875) (2, 4000) (3, 4125) etc.
This shows that for each increase by one ton of sugar, the cost goes up $125
1)Cost of 1 ton = $ 2000
Cost of 2 ton = $3500
Cost of 3 ton = $5000
$ 1500 increase for each of ton of sugar being transported.
2) (1 , 2000) ; (2 , 3500)
Slope =
= 1500
I have been stuck on this maths question for 3 hours pls help

Answers
b) highest possible value is £214999.99
hope this helps!
Which of the following expressions is equivalent to "eight groups of four"?
A 8+4
B. (8 + 4)
C. 8 x 4
D. 4°
Answers
Answer:
Hey mate,here is your answer. Hope it helps you.
Step-by-step explanation:
The answer is c- 8 x 4. As there are 8 groups of 4 the easiest way to calculate is by multiplying them both. Repeated addition is known as multiplication.
A plumber charges $50 for a house call plus $40 for each hour worked. Let h represent the number of hours worked. Write an expression that shows how much the plumber charges for a job lasting h hours. Then find how much the plumber charge for a job lasting 3 hours.
Answers
Answer:
x = 50 + 40h
Step-by-step explanation:
below the paraboloid z = 18 − 2x2 − 2y2 and above the xy-plane
Answers
Answer:
y
2
=−
2
z
+7
Steps for Solving Linear Equation
z=18−2×2−2y2
Multiply 2 and 2 to get 4.
z=18−4−2y
2
Subtract 4 from 18 to get 14.
z=14−2y
2
Swap sides so that all variable terms are on the left hand side.
14−2y
2
=z
Subtract 14 from both sides.
−2y
2
=z−14
Divide both sides by −2.
−2
−2y
2
=
−2
z−14
Dividing by −2 undoes the multiplication by −2.
y
2
=
−2
z−14
Divide z−14 by −2.
y
2
=−
2
z
+7
Step-by-step explanation:
the given equation defines a paraboloid that lies below the plane z=0. Specifically, it is situated above the xy-plane, which means that the z-values of all points on the surface are greater than or equal to zero.
we can break down the equation z=18-2x^2-2y^2. This equation represents a paraboloid with its vertex at (0,0,18) and axis of symmetry along the z-axis. The first term 18 is the z-coordinate of the vertex and the last two terms -2x^2 and -2y^2 determine the shape of the paraboloid.
Since the coefficient of x^2 and y^2 terms are negative, the paraboloid is downward facing and opens along the negative z-axis. Therefore, all points on the paraboloid have z-values less than 18. Additionally, since the paraboloid is situated above the xy-plane, its z-values are greater than or equal to zero.
the paraboloid defined by the equation z=18-2x^2-2y^2 is situated below the plane z=0 and above the xy-plane. Its vertex is at (0,0,18) and it opens along the negative z-axis.
To know more about paraboloid, visit:
https://brainly.com/question/30925041
#SPJ11
Is 3x2 5x 9 x2 7x 3 a quadratic equation?
Answers
Yes, this equation is a quadratic equation.
What is a quadratic equation?
Quadratic equation are the polynomial equations of degree 2 in one variable of type f(x) = ax² + bx + c = 0 where a, b, c ∈ R and a ≠ 0.
The given equation 3x² + 5x + 9x² + 7x + 3 = 0 can be written as 12x² + 12x +3 = 0, which is a general form of quadratic equation where a = 12, b = 12 and c =3.
Hence, the equation is a quadratic equation.
To learn more about quadratic equations click:
https://brainly.com/question/29011747
#SPJ4
6x + 2 = 26 what is the answer
Answers
Answer: x=4
Step-by-step explanation:
Answer:
x=4
Step-by-step explanation:
6x+2=26
Subtract 2 from both sides to isolate the variable
6x=24
Divide by 6
x=4
Which expression best estimates 6 3/4 divided by 1 2/3
A 7 divided by 2
B 6 divided by 1
C 8 divided by 3
D 3 divided by 2
Answers
Answer:
B is my answer si no sorry
given the argument: e ⊃ j / b ⊃ q / d ⊃ (j • ∼ q) // (e • b) ≡ d
a. Uncogent.
b. Sound.
c. Valid.
d. Invalid.
e. Cogent.
Answers
The correct option is : c. Valid
Does the logical relationship between the premises and conclusion in the given argument hold true?
Yes, the logical relationship between the premises and conclusion in the given argument holds true.
To evaluate the given argument, we can break it down into its premises and conclusion:
Premises:
1.e ⊃ j (If e, then j)
2.b ⊃ q (If b, then q)
3.d ⊃ (j • ∼q) (If d, then (j and not q))
Conclusion:
(e • b) ≡ d ((e and b) if and only if d)
To determine the validity and cogency of the argument, we need to assess whether it is logically valid and whether its premises are true.
Validity: An argument is valid if the truth of its premises guarantees the truth of its conclusion. Let's analyze each premise:
1.e ⊃ j (If e, then j)
This premise asserts a conditional statement. If e is true, then j must also be true. This premise seems reasonable.
2.b ⊃ q (If b, then q)
Similar to the first premise, this premise asserts a conditional statement. If b is true, then q must also be true. This premise seems reasonable as well.
3.d ⊃ (j • ∼q) (If d, then (j and not q))
Once again, this premise states a conditional relationship. If d is true, then both j and not q must be true. This premise also seems reasonable.
Now let's consider the conclusion:
(e • b) ≡ d ((e and b) if and only if d) This conclusion states an equivalence, asserting that (e and b) is true if and only if d is true.
Given that all the premises are reasonable and logically valid, we can conclude that the argument is valid.
Therefore, the correct answer is:
c. Valid.
To learn more about the logical relationship between the premises and conclusion in the given argument hold true from the given link
https://brainly.com/question/30466861
#SPJ4
please help will be marking Brainliest

Answers
Answer:
A or b not to sure
Step-by-step explanation:
Help I need this?!!!!???!,!?

Answers
Answer:
i hate my life
Step-by-step explanation:
a tree, t, has 24 leaves and 13 internal nodes. all internal nodes have degree 3 or 4. how many internal nodes of degree 4 are there? how many of degree 3?
Answers
There are 3 internal nodes with degree 4 and 10 internal nodes with degree 3 in the tree t.
Let x be the number of internal nodes with degree 4, and y be the number of internal nodes with degree 3.
1. x + y = 13 (total internal nodes)
2. 4x + 3y = t - 1 (sum of degrees of internal nodes)
Since t has 24 leaves and 13 internal nodes, there are 24 + 13 = 37 nodes in total. So, t = 37 and we have:
4x + 3y = 36 (using t - 1 = 36)
Now, we can solve the two equations:
x + y = 13
4x + 3y = 36
First, multiply the first equation by 3 to make the coefficients of y equal:
3x + 3y = 39
Now, subtract the second equation from the modified first equation:
(3x + 3y) - (4x + 3y) = 39 - 36
-1x = 3
Divide by -1:
x = -3/-1
x = 3
Now that we have the value of x, we can find the value of y:
x + y = 13
3 + y = 13
Subtract 3 from both sides:
y = 13 - 3
y = 10
So, there are 3 internal nodes with degree 4 and 10 internal nodes with degree 3 in the tree t.
Learn more about nodes here:
https://brainly.com/question/31115287
#SPJ11
.find all lower triangular 3×3 matrices x such that x3 is the zero matrix.
Answers
The lower triangular 3×3 matrices x such that x³ is the zero matrix have the form : x = [0 0 0,g h 0,0 0 0] where g and h any real number.
To find all lower triangular 3×3 matrices x such that x³ is the zero matrix, set up the equation x³ = 0 and solve for the elements of x. Let's represent a generic lower triangular matrix as:
x = [a b 0
d e f
g h i]
Multiplying x by itself three times,
x³ = [a b 0] × [a b 0] × [a b 0]
= [a²+bd ab 0]
[ad+be ae+bf b²]
[ag+bh ah+bh 0]
Setting this result equal to the zero matrix, we have:
a²+bd = 0
ab = 0
ad+be = 0
ae+bf = 0
b² = 0
ag+bh = 0
ah+bh = 0
0 = 0
0 = 0
0 = 0
From the equations above, deduce the following conditions for the elements of x:
a = 0
b = 0
d = 0
e = 0
f = 0
g can be any real number
h can be any real number
i = 0
To know more about triangular here
https://brainly.com/question/30950670
#SPJ4
I will give you 10B points plus mark someone again for the Brainliest if you get this right. a:15 b:7 c:4

Answers
For this expression,a=15,b=7 and c=4
Hope it helpsGood luck on your assignment
how do i do this pls explain the steps
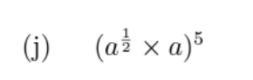
Answers
Answer:
\(a^{\frac{15}{2} }\)
Step-by-step explanation:
Using the rules of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
\((a^m)^{n}\) = \(a^{mn}\)
(\(a^{\frac{1}{2} }\) × a)^5
= \((a^{\frac{1}{2}+1) }\)^5
= \((a^{\frac{3}{2}) } ^{5}\)
= \(a^{\frac{15}{2} }\)
Which expression is equivalent to 30 + 8?
Answers
Answer:
38
Step-by-step explanation:
please help (probability question)!

Answers
Answer:
There are 64 possible outcomes.
Step-by-step explanation:
Each flip has 2 options, heads or tails.
head tail
One flip has 2 outcomes. When you flip again, you can get this set of 4 outcomes:
head-head tail-head
head-tail tail-tail
Then when you flip a third coin, each of those cases has 2 cases itself. As you can see, each flip that is added, the total number of outcomes doubles. For 6 flips, you do 2x2x2x2x2x2 or \(2^{6}\).
If the perimeter of square X is triple that of square Y, then the are of X is how many times the area of Y?
Answers
Answer:3 more than y i think srry if im wrong
Step-by-step explanation:
find all acute angles x such that sin2xsin3x=cos2xcos3x. if the sum of these angles can be written in the form aπb in lowest terms, what is a b?
Answers
For all acute angles x such that the equation sin(2x)sin(3x) = cos(2x)cos(3x), the sum of the angles can be written as aπb in lowest terms, where a = 1 and b = 3 then, the answer is 1/3.
For all acute angles x satisfying the equation sin(2x)sin(3x) = cos(2x)cos(3x), we can use trigonometric identities to simplify the equation.
Using the double-angle identity for sine, we have:
sin(2x) = 2sin(x)cos(x)
Similarly, using the double-angle identity for cosine, we have:
cos(2x) = cos^2(x) - sin^2(x)
Applying these identities, the equation becomes:
2sin(x)cos(x)sin(3x) = cos^2(x)cos(3x) - sin^2(x)cos(3x)
Expanding further, we have:
2sin(x)cos(x)sin(3x) = cos(x)[cos^2(x)sin(3x) - sin^2(x)sin(3x)]
Dividing both sides by cos(x) (assuming cos(x) ≠ 0), we get:
2sin(x)sin(3x) = cos^2(x)sin(3x) - sin^2(x)sin(3x)
Now, we can factor out sin(3x) from both terms on the right side:
2sin(x)sin(3x) = sin(3x)[cos^2(x) - sin^2(x)]
Applying the Pythagorean identity cos^2(x) = 1 - sin^2(x), the equation simplifies to:
2sin(x)sin(3x) = sin(3x)(1 - 2sin^2(x))
If sin(3x) ≠ 0, we can cancel out sin(3x) from both sides:
2sin(x) = 1 - 2sin^2(x)
Rearranging the terms, we get a quadratic equation in terms of sin(x):
2sin^2(x) + 2sin(x) - 1 = 0
Solving this quadratic equation, we find two possible values for sin(x):
sin(x) = (-1 ± sqrt(3))/2
Since we are considering acute angles, we only take the positive value:
sin(x) = (-1 + sqrt(3))/2
To find the corresponding angles, we can use the inverse sine function:
x = arcsin((-1 + sqrt(3))/2)
Using a calculator, we find:
x ≈ π/3
Therefore, the only acute angle x satisfying the equation is x = π/3.
The sum of the angles can be written as aπb in lowest terms, where a = 1 and b = 3. Thus, the answer is 1/3.
To know more about trigonometric identities refer here :
https://brainly.com/question/31837053#
#SPJ11
The perimeter of the figure below is 61.1 m. Find the length of the missing side.

Answers
Answer:
I believe it would be 12.9
Step-by-step explanation:
perimeter is all of the outside lengths combined. if you take the 61.1 and subtract the lengths it gives you, the remaining length should be your answer
can someone find a limit at a location where there is a hole in a graph, such as where a point has been removed or where a graph abruptly stops? why or why not? give an explanation that includes the consideration of (in) the limit from the left, (ii) the limit from the right, and (iii) the general limit.
Answers
Yes, it is possible to find a limit at a location where there is a hole in a graph , such as where a point has been removed or where a graph abruptly stops.
This is because the limit of a function is defined as the value that the function approaches as x approaches a given value. In the case of a hole in the graph, the limit is found by looking at the limit from the left, the limit from the right, and the general limit.
The limit from the left is the limit of the function as x approaches the hole from the left. The limit from the right is the limit of the function as x approaches the hole from the right. The general limit is the overall limit of the function at the point where the hole appears. By considering all of these limits, it is possible to determine the overall limit of the function at the point where the hole is present.
Learn more about limits:
https://brainly.com/question/30451475
#SPJ4
