Answers
Answer:
24 cm²
Step-by-step explanation:
The area of a rhombus is half the product of its diagonals.
\(\boxed{\sf Area\;of\;a\;rhombus=\dfrac{diagonal\;1 \cdot diagonal\;2}{2}}\)
Therefore, to find the area of the rhombus, we need to find the lengths of the diagonals AC and BD.
The diagonals of a rhombus are perpendicular bisectors of each other.
The point of intersection of the diagonals of rhombus ABCD is point O.
We can use the given information to find the lengths of BO and OC, then double these to find diagonals AC and BD.
The sides of a rhombus are equal in length. Therefore, if the perimeter of rhombus ABCD is 20 cm, each side length is 5 cm.
Therefore, the hypotenuse of right triangle BOC is BC = 5 cm.
If the ratio of AC : BD = 4 : 3, then the ratio of OC : BO = 2 : 1.5.
Let OC = 2x and BO = 1.5x.
Use Pythagoras Theorem to find the value of x.
\(\begin{aligned}BO^2+OC^2&=BC^2\\(1.5x)^2+(2x)^2&=5^2\\1.5^2x^2+2^2x^2&=25\\2.25x^2+4x^2&=25\\6.25x^2&=25\\x^2&=4\\\sqrt{x^2}&=\sqrt{4}\\x&=2\end{aligned}\)
Therefore, to find the lengths of OC and BO, substitute x = 2:
\(OC = 2x = 2(2) = 4\; \sf cm\)
\(BO = 1.5x = 1.5(2) = 3\; \sf cm\)
As the diagonals of a rhombus bisect each other:
\(AC = 2\cdot OC=2 \cdot 4 = 8\; \sf cm\)
\(BD = 2\cdot BO=2 \cdot 3 = 6\; \sf cm\)
Finally, substitute the lengths of the diagonals into the formula for the area of a rhombus:
\(\begin{aligned}\textsf{Area of rhombus $ABCD$}&=\sf \dfrac{diagonal\;1 \cdot diagonal\;2}{2}}\\\\&= \dfrac{AC \cdot BD}{2}\\\\&=\dfrac{8 \cdot 6}{2}\\\\&=\dfrac{48}{2}\\\\&=24\; \sf cm^2 \end{aligned}\)
Therefore, the area of rhombus ABCD is 24 cm².
Related Questions
The proportion of a normal distribution located between z = .50 and z = -.50 is ____.
Answers
The proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
We have,
A normal distribution located between z = 0.50 and z = -0.50,
So,
Now,
From the Z-score table,
We get,
The Probability corresponding to the Z score of -0.50,
i.e.
P(-0.50 < X < 0) = 0.191,
And,
The Probability corresponding to the Z score of -0.50,
i.e.
P(0 < X < 0.50) = 0.191,
Now,
The proportion of a normal distribution,
i.e.
P(Z₁ < X < Z₂) = P(Z₁ < X < 0) + P(0 < X < Z₂)
Now,
Putting values,
i.e.
P(-0.50 < X < 0.50) = P(-0.50 < X < 0) + P(0 < X < 0.50)
Now,
Again putting values,
We get,
P(-0.50 < X < 0.50) = 0.191 + 0.191
On solving we get,
P(-0.50 < X < 0.50) = 0.382
So,
We can write as,
P(-0.50 < X < 0.50) = 38.2%
So,
The proportion of a normal distribution is 38.2%.
Hence we can say that the proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
Learn more about normal distribution here
https://brainly.com/question/13759327
#SPJ4
Which angle is formed by a secant and tangent line?
A) ANG
B) GSE
B) EGS
C) NGL
Answers
The angle formed by a secant and tangent line is GSE (Given-Secant-Exterior).
A tangent is a straight line or curve that touches a given curve exactly once but does not cross it. The tangent is a fundamental concept in geometry and calculus that is used to study the behavior of functions at a specific point.
An external angle is the angle formed by a secant and tangent line at a point on a circle. The abbreviation for this angle is EGS (External Angle-Secant-Tangent).
A secant line intersects a circle at two points, whereas a tangent line intersects the circle at only one. The external angle is formed at the point of tangency by the intersection of the secant and tangent lines outside the circle.
Full question.
Which angle is formed by a secant and tangent line?
A) ANG
B) GSE
B) EGS
C) NGL
To learn more about tangent.
https://brainly.com/question/19424752
#SPJ4

(x+4)\left(y^{2}+1\right) d x+y\left(x^{2}+3 x+2\right) d y=0 implicit
Answers
The implicit solution to the given equation is \(x(y^{2} + 3y + x^{2} + 3x + 4) + 4y^{2} + 2y + 4 = 0\)
To find the implicit solution to the given equation, we can rearrange it in the form of \(F(x, y) = 0\).
Starting with the given equation:
\((x+4)(y^{2}+1) dx + y(x^{2}+3x+2) dy = 0\)
Expanding the terms:
\(xy^{2} + x + 4y^{2} + 4 + yx^{2} + 3yx + 2y dy = 0\)
Combining like terms:
\(yx^{2} + xy^{2} + 3yx + x + 4y^{2} + 2y + 4 = 0\)
Rearranging the terms:
\(x(y^{2} + 3y + x^{2} + 3x + 4) + 4y^{2} + 2y + 4 = 0\)
Therefore, the implicit solution to the given equation is:
\(x(y^{2} + 3y + x^{2} + 3x + 4) + 4y^{2} + 2y + 4 = 0\)
To learn more about implicit click here:
/brainly.com/question/32513056
#SPJ11
To win a carnival game, you have to shoot a stream of water into a clown's mouth. the clown face is painted on a rectangular piece of wood that measures 16 inches by 12 inches. the clown's mouth is a circle with a diameter of 3 inch. what is the probability that your water will hit the clown's mouth?
write the probability as a percentage, rounded to the nearest tenth.
Answers
The probability will be 0.037 or 3.7% when it is rounded to the nearest tenth.
To calculate the probability of hitting the clown's mouth, we need to compare the area of the clown's mouth to the total area of the rectangular wood piece.
The area of the clown's mouth can be found using the formula for the area of a circle: A = π * (r^2), where r is the radius. In this case, the diameter is given as 3 inches, so the radius is 1.5 inches.
Plugging the values into the formula, we get A = π * (1.5^2) = 7.065 square inches. The total area of the rectangular wood piece is 16 inches * 12 inches = 192 square inches.
Therefore, the probability of hitting the clown's mouth is 7.065 / 192 ≈ 0.0367, which rounds to 0.037 or 3.7% when expressed as a percentage rounded to the nearest tenth.
To know more about probability, refer here :
https://brainly.com/question/32117953#
#SPJ11
For each ordered pair, determine whether it is a solution to the system of equations. -18x+2y=8 and y=9x+4
Answers
For the given system of equations, no solution is possible.
What is the system of equations?One or many equations having the same number of unknowns that can be solved simultaneously are called simultaneous equations. And the simultaneous equation is the system of equations.
Given:
The system of equations,
-18x + 2y = 8 {equation 1}
y = 9x + 4 {equation 2}
Substitute the value of y from equation 2 to equation 1,
we get,
-18x + 18x + 8 = 8
0 = 0
That means, the lines of the equation are parallel to each other.
Therefore, no solution is possible for the system.
To learn more about the system of equations;
brainly.com/question/13729904
#SPJ1
Can someone please help me with this? Show work please.

Answers
Answer:
8 feet.
Step-by-step explanation:
Area of rectangle:Before remodeling:
width = 9 ft
Area = 108 ft²
\(\boxed{length = \dfrac{Area}{width}}\)
\(=\dfrac{108}{9}\\\\= 12 \ ft\)
After remodeling:
width = 9 ft
Area = 180 ft²
\(length = \dfrac{180}{9}\\\)
= 20 ft
length after remodeling = 20 ft
To find the length of the added portion, subtract the length of the living room before modeling from the length after remodeling.
length of the added portion = 20 - 12
= 8 ft
if the observed t value exceeds the critical t value, then the difference between the sample means is most likely ____.
Answers
If the observed t-value exceeds the critical t-value, then the difference between the sample means is most likely statistically significant.
In other words, the difference between the sample means is unlikely to have occurred by chance and is likely due to a real difference in the population means. The direction and magnitude of the difference must be further examined using effect size measures and confidence intervals.
Therefore, the most suitable value to be fit in the blank space of the given incomplete statement is, statistically significant.
Learn more about If the sample means :
https://brainly.com/question/31101410
#SPJ4
The probability that a household owns a pet is 0. 55. Suppose there are 5 houses on a block. Assuming each household is independent. What is the probability that all five households will have pets?
Answers
If the probability that a household owns a pet is 0.55 then the probability that all households will have pets is equal to 0.0503.
Given that the probability that a household owns a pet is 0.55 and there are 5 houses on a block.
We are required to calculate the probability that all the five households will have pets.
Probability is basicallly the chance of happening an event among all the events possible. It cannot be negative.
Binomial probability distribution is basically the probability calculations but in different combinations.
In this we have to calculate the probability that all the houses will have the pets then the probability that all five households will have pets is equal to \(5C_{5}(0.55)^{5} (1-0.55)^{0}\)
=1(0.0503)\((0.45)^{0}\)
=1*0.0503*1
=0.0503
Hence the probability that all the five households will have pets is equal to 0.0503.
Learn more about probability at https://brainly.com/question/24756209
#SPJ4
A turtle swims 15 kilometers in 9 hours. How far does the turtle swim in 24 hours?
Answers
Answer:
about 40 kilometers
Step-by-step explanation:
Ayshab walked x miles at 4 mph.
She then walked 2x miles at 3 mph.
Find Ayshab's average speed for the whole journey.
Give your answer as a mixed number.

Answers
Answer: Ayshab's average speed for the whole journey = \(3\dfrac{3}{11}\text{ mph}\)
Step-by-step explanation:
Formula: Speed = \(\dfrac{Distance}{Time}\)
i.e. Time = \(\dfrac{Distance}{Speed}\)
If Ayshab walked x miles at 4 mph, then time taken by him = \(\dfrac{x}{4}\) hours
If she then walked 2x miles at 3 mph, then time for this period = \(\dfrac{2x}{3}\) hours
Average speed = \(\dfrac{Total \ distance}{Total\ time}\)
\(=\dfrac{x+2x}{\dfrac{x}{4}+\dfrac{2x}{3}}\\\\\\=\dfrac{3x}{x(\dfrac{1}{4}+\dfrac{2}{3})}\\\\\\=\dfrac{3}{\dfrac{3+8}{12}}\\\\\\=\dfrac{3\times12}{11}\\\\=\dfrac{36}{11}\\\\=3\dfrac{3}{11}\text{ mph}\)
Hence, Ayshab's average speed for the whole journey = \(3\dfrac{3}{11}\text{ mph}\)
Ayshab's average speed for the whole journey is 36/11 mph and this can be determined by using the formula of average speed.
Given :
Ayshab walked x miles at 4 mph.She then walked 2x miles at 3 mph.The formula of speed is given by:
\(\rm Speed = \dfrac{Distance }{Time}\)
\(\rm Time = \dfrac{ Distance}{Speed}\)
Now, the time taken by Ayshab to walk x miles at 4 mph is :
\(\rm t_1 = \dfrac{x}{4}\)
Now, the time taken by Ayshab to walk 2x miles at 3 mph is:
\(\rm t_2 = \dfrac{2x}{3}\)
Now, the average speed is given by the formula:
\(\rm Avg. \; Speed = \dfrac{Total \;Distance}{Total \; Time}\)
\(=\dfrac{x+2x}{\dfrac{x}{4}+\dfrac{2x}{3}}\)
\(= \dfrac{36}{11}\)
Ayshab's average speed for the whole journey is 36/11 mph.
For more information, refer to the link given below:
https://brainly.com/question/12577966
Find the solution to the system of equations.
X + 4y- 5z = -6
X + 4y-4z=-2
X + 5y-4z= 1
O A. x = 2, y = 4, z = 5
O B. x = 2, y = 3, z= 4
O C. x = 5, y = 11, z = -12
O D. x= 5, y = 5, z= 3

Answers
Answer:
B
Step-by-step explanation:
First you are going to have to solve for one of the variables in the terms of the other two. The easiest one of these to start with is x.
If you take the first equation, x+4y-5z=-6 and solve for x you get
x=5z-4y-6
Now you can plug that into another equation and solve for another one of the variables. Lets use equation #2. Plugging in the definition of x into the equation you get;
(5z-4y-6)+4y-4z=-2
Simplify
z-6=-2
Conveniently, the y terms cancelled out. And therefore we know
z=4
(From there, we can determine that B is the right answer because it is the only one that gives z=4. I will walk you through the rest of the answer though)
Taking our new value of z, we can pug that value into our original x equation yielding;
x=20-4y-6
simplify
x=14-4y
Using this information, we can plug it into equation #3
(14-4y)+5y-16=1
simplify
y-2=1
solve
y=3
Now we just plug the new values of y and z into the first equation to get the value of x.
x+12-20=-6
simplify
x-8=-6
solve
x=2
Therefore;
x=2
y=3
z=4
hi i need help with this

Answers
Answer:
15 in
Step-by-step explanation:
d^2 = w^2 + l^2
25^2 = 20^2 + l^2
l^2 = 225
l = 15
I need help ASAP
Also I need to show work on it because it is for my homework

Answers
Answer:4.5
Step-by-step explanation:

the route used by a certain motorist in commuting to work contains two intersections with traffic signals. the copyright 2016 cengage learning. all rights reserved. may not be copied, scanned, or duplicated, in whole or in part. due to electronic rights, some third party content may be suppressed from the ebook and/or echapter(s). editorial review has deemed that any suppressed content does not materially affect the overall learning experience. cengage learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. 66 chapter 2 probability probability that he must stop at the first signal is .4, the analogous probability for the second signal is .5, and the probability that he must stop at at least one of the two signals is .7. what is the probability that he must stop a. at both signals? b. at the first signal but not at the second one? c. at exactly one signal?
Answers
a. The probability that he must stop at both signals is 0.2.b. The probability that he must stop at the first signal but not at the second one is 0.2.
c. The probability that he must stop at exactly one signal is 0.5.
a. The probability that he must stop at both signals is equal to the product of the individual probabilities of stopping at each signal, which is 0.4 x 0.5 = 0.2.
b. The probability that he must stop at the first signal but not at the second one is equal to the probability of stopping at the first signal only, which is 0.4.
c. The probability that he must stop at exactly one signal is equal to the sum of the probability of stopping at the first signal and the probability of stopping at the second signal, which is 0.4 + 0.5 = 0.5.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
Which is the correct first step in finding the area of the base of a cylinder with a volume of 140 pi cubic meters and a height of 12 meters?
A.V = B h. 12 = B (140 pi)
B.V = B h. V = 140 pi + (12)
C.V = B h. V = 140 pi (12)
D.V = B h. 140 pi = B (12)
Answers
Answer:
I believe it's A
Step-by-step explanation:
I'm not so sure because I did this a while back
pic below................................
answer ASAP
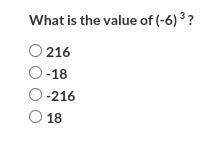
Answers
Answer:
The answer is C.-216
Step-by-step explanation:
Answer:
C.)-216
Step-by-step explanation:
Since -6 is negative, it makes it become a positive when multiplyed, and then back to a negative when multiplyed again.
Consider a discrete random variable, X. Identify the correct statement for using the cumulative distribution function (cdf), F(x), to solve the probability below. P(X<12) F(13)1−F(12) F(13)−F(12) F(12)−F(11)1−F(13)F(12) None of the above. F(11) 10 0/6points Consider a discrete random variable, X. Identify the correct statement for using the cumulative distribution function (cdf), F ( (X ), to solve the probability below. P(X≤100) 1−F(100) F(99) ×O(100)−F(99) F(101) F(100) F(101)−F(100) 1−F(99) None of the above
Answers
The correct statement for using the cumulative distribution function (cdf), F(x), to solve the probability P(X<12) is: F(12) - F(11), We subtract the cdf value at x-1 from the cdf value at x.
The cumulative distribution function (cdf), denoted as F(x), gives the probability that a random variable X takes on a value less than or equal to x. In this case, we are interested in finding the probability that X is less than 12, which can be expressed as P(X<12).
To calculate this probability using the cdf, we need to find the difference between the cdf values at 12 and 11. The cdf value at 12, denoted as F(12), gives the probability that X is less than or equal to 12. Similarly, the cdf value at 11, denoted as F(11), gives the probability that X is less than or equal to 11.
Since we want to find the probability that X is strictly less than 12, we subtract the probability that X is less than or equal to 11 from the probability that X is less than or equal to 12. Mathematically, this can be written as F(12) - F(11).
Therefore, the correct statement for using the cdf to solve P(X<12) is F(12) - F(11).
Learn more about Discrete random variable: brainly.ph/question/2453571
#SPJ11
will reward the brainliest


Answers
Question 9 x> 2
Question 9: y>0
The product of (a − b)(a − b) is a^2 − b^2
Sometimes
Always
Never
Answers
Answer:
Sometimes
Step-by-step explanation:
Expanding (a-b)(a-b), we get a^2 - 2ab - b^2. This is equal to a^2 - b^2 when a=0 and b=0.
A painter needs to obtain a particular shade of green paint by mixing yellow paint with blue paint in the ratio 3:5. If he buys 45 litres of yellow paint, how many litres of blue are required?
Answers
Answer:
75 litres of Blue
Step-by-step explanation:
Divide the amount of yellow liters by 3, you'll get 15. To get the amount of blue needed, you multiply 5 by 15.
a physical education teacher fournd that 62 1/2% of the students exceeded the minimum standards. which represents the part of the students who exceeded the standards?
Answers
According to the given statement, 62 1/2% represents the part of the students who exceeded the minimum standards.
The part of the students who exceeded the minimum standards is 62 1/2%.
To find the part of the students who exceeded the standards, we need to look at the percentage mentioned in the question. The question states that 62 1/2% of the students exceeded the minimum standards. This means that 62 1/2% is the part or proportion of students who exceeded the standards.
Therefore, 62 1/2% represents the part of the students who exceeded the minimum standards.
To know more about proportion visit:
https://brainly.com/question/30241688
#SPJ11
Dr.Osborne has scheduled Anita Blanchette for a spirometry test and wants you to telephone her the day before the test to prepare her so that optimal results are obtained.
1.) What information do you give Anita before her spirometry so that the best test results can be obtained?
2.) How would you explain the rationale for the performance of this procedure?
Answers
To ensure the best test results, Anita should be provided with the following information before her spirometry:
1. Instructions for taking the test: Anita should be thoroughly explained about how the spirometry test works and what steps she needs to follow. This includes taking a deep breath and blowing as hard as she can into the spirometer mouthpiece. It is important to emphasize that she needs to repeat this procedure a few times and take deep breaths between each exhale.
2. Emphasize the importance of taking medication as prescribed: Anita should be reminded of the importance of taking her medications as prescribed, including on the day of the test. It is crucial for her to bring her medications to the test appointment.
3. Avoid certain foods and drinks: Anita should be informed to avoid consuming certain substances before the spirometry test, such as caffeine, alcohol, and heavy meals. These can potentially affect the accuracy of the test results.
4. Arrive early for the test: Anita should be advised to arrive early for the test to allow herself sufficient time to relax and calm down before the procedure. This can help ensure more accurate results.
The rationale behind providing these instructions and information is that spirometry is a lung function test that measures the amount and speed of air being breathed in and out. By following the instructions and guidelines, Anita can achieve optimal results, aiding in the diagnosis and assessment of lung conditions.
Learn more about spirometry and its significance in assessing lung function:
https://brainly.com/question/18155241
#SPJ11
What is 18(54)+72(929)?
Answers
EXPLANATION
Given the operation 18(54)+72(929), by applying the distributive property:
= 972 + 66,888
Adding numbers:
= 67,860
The solution is 67,860
Which of the following is a run on sentence serious answers only

Answers
Explanation: it run on
You have only $1 bills and $5 bills in your wallet. You have 33 bills worth a total of $93. How many of each type of bill do you have?
Answers
Answer:
you would have 3 1's and 10 9's so sorry if this is wrong
three mutually tangent spheres of radius 1 rest on a horizontal plane. a sphere of radius 2 rests on them. what is the distance from the plane to the top of the larger sphere?
Answers
According to the statement the distance from the plane to the top of the larger sphere is 3 + 2 = 5 units.
The distance from the plane to the top of the larger sphere can be found by considering the arrangement of the spheres.
We have three smaller spheres of radius 1 that are mutually tangent to each other and the plane.
On top of them, there is a larger sphere of radius 2.
Let's denote the distance from the plane to the center of the larger sphere as h.
Since the spheres are tangent to each other, the distance from the plane to the top of the larger sphere will be equal to the sum of the radii of the smaller spheres (3 x 1 = 3) plus the radius of the larger sphere (2).
Therefore, the distance from the plane to the top of the larger sphere is 3 + 2 = 5 units.
To know more about tangent visit :
https://brainly.com/question/10053881
#SPJ11
Which method is best for root finding?
Answers
Answer:
on the value of the root may produce a value of the polynomial at the approximate root that is of the order of. For avoiding these problems, methods have been elaborated, which compute all roots simultaneously, to any desired accuracy. Presently the most efficient method is Aberth method.
how to determine sample size needed for confidence intercal when population standard deviation not known
Answers
When the population standard deviation is not known, the sample size needed for a confidence interval can be determined using the t-distribution.
The t-distribution is used to calculate the margin of error, which is the amount of variation that is allowed in the sample results. The sample size needed for a confidence interval is determined by calculating the critical value of the t-distribution for a given level of confidence and degree of freedom. The degree of freedom is the number of independent observations in the sample minus one.
The confidence level determines the critical value of the t-distribution, which is used to calculate the margin of error. The sample size is then calculated by dividing the margin of error by the desired confidence level. This method allows us to determine the sample size needed for a confidence interval even when the population standard deviation is unknown.
Learn more about t-distribution here:
https://brainly.com/question/24277447
#SPJ4
4x7x2 1\2 I really need a good answer
Answers
Answer:
70
Step-by-step explanation:
Hello there! Let's work this through:
Firstly, we might want to simply 2 1/2 into 5/2, for simplification.
So, we now have 4 * 7 * 5/2
Simplifying we have \(\frac{4*7*5}{2}\)
We see that we can easily simplify 4/2 into 2 * 7 * 5
Further simplifying we get 10*7
Last bit and we get our answer of 70
From here we get 2
Help please i dint get it pls answer

Answers
Answer: 7%
(Hope this is right.)
Step-by-step explanation:
Let's solve this using the information we have and an equation.
Shane: $32,000 - (Given)
Theresa: 18,000+14x, if x=1,160 - (Given)
---------------------------------------------------------------
Step two: (Theresa) 14(1,160) =16,240 (Algebra)
Step three: (Theresa) 18,000+16,240=34,240 (Algebra, given.) - cost of Theresa's car.
---------------------------------------------------------------
Finally,
They're asking for how much more she paid for her car as a percentage of what Shane paid.
34,240-32,000=2,240 and
2,240/32,000=0.07
0.07x100=7
Answer 7% more than what Shane paid.
