Answers
Answer:
The second graph.
Step-by-step explanation:
The first graph has a negative slope, so that can't be the right answer.
The last graph isn't steep enough to show a rate of 2.5.
This leaves us with the middle graph which is correct.
Related Questions
i need help i suck at these

Answers
Answer:
i will help
Step-by-step explanation:
2 hours=21.50
3 hours= 32.25
4 hours= 43.00
Answer:
2 - 21.5
3 - 32.25
4 - 43
Step-by-step explanation:
10.75 × 2 = 21.5 ÷ 2 = 10.75
10.75 × 3 = 32.25 ÷ 3 = 10.75
10.75 × 4 = 43 ÷ 4 = 10.75
f(x). - graph with a line going through (-2.8) and (-4,0)
g(x) = 3x - 4
h(x)
Kelly had 4 apples
in her kitchen on
Monday. On
Tuesday, only 1
was left.
x. j(x)
-2. -2
2. 10
6. 22
Compare and contrast these four functions using complete sentences. Focus on the
slope and y-intercept first, and then on any additional properties of each function.
(10 points)
Answers
One possibility could be :
y = x - 3
wherein:
x : number of apples on Monday
y : number of apples on Tuesday, the day after
Hope I helped you! :)
Have a great day/night!!
The bearing of two parts Q and R froma point p are 030° and 120° respectively. If pq =12m
Answers
The distance between point P and point R is 12 - 6√3 m.
The given problem states that the bearing of two parts Q and R from point P are 030° and 120° respectively and if PQ = 12m.
Now, we have to calculate the distance between point P and point R.
For this, we can use cosine rule as follows:
PR² = PQ² + QR² - 2PQ × QR × cos(∠PQR)
Also, ∠PQR = ∠QPR - ∠PQR
Taking ∠QPR as 90°, we get:
∠PQR = 90° - 120°
= -30° (because PQR is an obtuse angle)
Therefore, cos(∠PQR) = cos(-30°)
Now, cos(-30°) = cos(30°)
= √3/2
Thus, PR² = PQ² + QR² - 2PQ × QR × √3/2
Putting the given values in this equation, we get:
PR² = 12² + QR² - 2 × 12 × QR × √3/2
⇒ PR² = 144 + QR² - 12QR√3
Since we know that PR = QR × sin(∠QPR), we can put this value of PR in the above equation to get:
QR² sin²(∠QPR) = (QR × sin(∠QPR))²
= 144 + QR² - 12QR√3
We can further simplify this equation to get:
QR = 12(2 - √3) or
QR = 12(2 + √3)
Now, since QR is positive, we can take only QR = 12(2 - √3)
As we have now calculated the value of QR, we can use the sine rule to find the length of PR.
sin(∠PQR) = PR/QR
Since ∠PQR = ∠QPR + ∠QRP
= 120° - 30°
= 90°
Therefore, sin(∠PQR) = sin(90°)
= 1
Thus, PR = QR × sin(∠QPR)
= 12(2 - √3) × sin(30°)
= 12(2 - √3)/2
= 12 - 6√3
To learn more on cosine rule:
https://brainly.com/question/30766161
#SPJ11
pls Solve my question

Answers
hope this will help you more

Factor -3x^2-23x+8. Please Help
Answers
Answer:
-(x+8)(3x-1)
Step-by-step explanation:
Take out the - sign, then factor as if it is positive.
Select all the functions whose output is 4 when the input is 16.
A.
y = 2x
B. y=x?
2
= x
C.
y = x + 12
D.
y = x - 12
E. y = 1
x
Answers
Answer:
Please check your post. I did the best I could.
Step-by-step explanation:
A. y = 2x 4 = 2*(16)? Nope
B. y=x? I don't understand the equation: y = x? 2 = x?????
C. y = x + 12 4 = 16 + 12? Nope
D. y = x - 12 Same???
E. y = 1 x 4 = 16? Nope
Let A and B be sets, and let f: A--B be a function. Suppose that A and B are finite sets, and that IAI = IBI. Prove that f is bijective if and only if f is injective if and only if f is surjective.
Answers
A function f: A--B is injective if each element in A maps to a unique element in B. It is surjective if every element in B has a corresponding element in A.
A bijective function is both injective and surjective, meaning that every element in A maps to a unique element in B, and every element in B has a corresponding element in A. If IAI = IBI, then there are the same number of elements in A and B. Therefore, if f is injective, every element in A must map to a unique element in B, leaving no elements in B without a corresponding element in A. This means that f is also surjective. Similarly, if f is surjective, then every element in B has a corresponding element in A, which means that f is also injective. Thus, f is bijective if and only if it is injective and surjective.
For more information on bijective function see:
https://brainly.com/question/30857450
#SPJ11
Select all the expressions that are equivalent to −5/6 / -1/3
Answers
Step-by-step explanation:
We need to find an expression for \(\dfrac{\dfrac{-5}{6}}{\dfrac{-1}{3}}\).
We can solve it as follows.
We know that,
\(\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}=\dfrac{a}{b}\times \dfrac{d}{c}\)
So,
\(\dfrac{\dfrac{-5}{6}}{\dfrac{-1}{3}}=\dfrac{-5}{6}\times -3\\\\=\dfrac{5}{2}\)
or
\(=2\dfrac{1}{2}\)
Hence, this is the required solution.
Select all of the true equations.
sin(27)=x/15
cos(63)=y/15
tan(27)=y/x
sin(63)=x/15
tan(63)=y/x

Answers
Answer:
cos(63)=y/15
tan(27)=y/x
sin(63)=x/15
Step-by-step explanation:
You need to memorize the definitions of all the trig functions. Then these types of problems will be easy for you. OK?
Lots of points, please help. Show work if you can.

Answers
Answer:
9) no solution
10) p = 4
11) n = 2
12) x = 3
Step-by-step explanation:
9) -5 ( -v - 4) + 4v = v + 20
5v + 20 + 4v = v + 20
no solution
10) -2 -3(p + 3) = -4p - 7
-2 - 3p - 9 = -4p - 7
-11 = -1p - 7
-4 = -1p
p = 4
11) 4(3 - 4n) = -24 + 2n
12 - 16n = -24 + 2n
-18n = -36
n = 2
12) 4(4 - 3x) = -23 + x
16 - 12x = -23 + x
-13x = -39
x = 3
hope this helps! :)
Answer:
Number 11 Answer = n = 2 || Number 12 Answer = x = 3
Step-by-step explanation:
12) 4(4 - 3x) = -23 + x
1. multiply 4 times 4 and 4 times 3x
16 - 12x = -23 + x
2. subtract 16 from itself 16 and 23
-12x = -39 + x
3. subtract x from itself and -12x
-13x = -39
4. Divide -13 from itself and -39
x = 3
11) 4(3 - 4n) = -24 + 2n
1. multiply 4 times 3 and 4 times 4n
12 - 16n = -24 + 2n
2. subtract 12 from itself and 24
-16n = -36 + 2n
3. subtract 2n from itself and -16n
-18n = -36
4. Divide -18n from itself and -36
n = 2
Homework
19. Elisa's math test score, with extra credit included, was 26/25.
What percent is this?
Answers
Answer:
100 is 4 times 25
25*4=100
so if we just multiply 26/25 we can find the percent
4*26/25=104/100
104%
Hope This Helps!!!
PLZZZZZZZZZZZ HELP!!!!!!!!!!!

Answers
Answer:
so for -16 just move 2 bars down (assuming it goes in twos) and just do that for the rest of them
Step-by-step explanation:
Write your answer as a fraction in simplest form.
6+(−434)+(−218)
Answers
\(\huge\text{Hey there!}\)
\(\large\boxed{\mathsf{6 + (-434) + (-218)}}\\\large\boxed{\mathsf{\rightarrow 6 \bf - 434 - 218}}\\\large\boxed{\rightarrow \mathsf{\bold{-428} - 218}}\\\large\boxed{\rightarrow \mathsf{\bf -646}}\\\large\boxed{\rightarrow \mathsf{\bold {- \dfrac{646}{1}} \approx -646\div1}}\\\\\\\large\text{We pretty much can't do anything to this so, your answer is: }\\\large\boxed{\mathsf{\bf -646}}\\\\\\\\\\\\\\\\\\\\\huge\text{Thus, your answer is: \boxed{\mathsf{-646}}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
-646 is the answer
hope it help
#Chloe919
#thanks for the points
#carry on learning
find the product of 16 and 24
Answers
Answer:
384 16 times 24 is equal to 384
Step-by-step explanation:
You just have to multiply them. 16 times 24 is 384.
True/False: When a form is created based on two or more tables, a relationship must be defined between queries.
Answers
True: When a form is created based on two or more tables, a relationship must be defined between queries.
True. When a form is created based on two or more tables, a relationship must be defined between queries in order to ensure that the form displays accurate data. Queries are used to pull data from multiple tables and present it in a single view, so it is important to define the relationships between these tables to avoid inconsistencies or errors in the displayed data. This ensures that the data from the related tables can be properly displayed and managed within the form.
When you drag and search a field from an "other" (unrelated) table, a new one-to-many relationship is created from the table in the list and the table from which you dragged the field. This relationship is established by Access, which does not enforce integrity by default.
Learn more about Tables:
brainly.com/question/10670417
#SPJ11
point K is the incenter of triangle PQR. what is m

Answers
Answer:
115 degrees
Step-by-step explanation:
The incenter is where the angle bisectors of a triangle meet. So \(m\angle{PQK}=15^\circ \text{ and } m\angle{PQR}=30^\circ\).
To find the measure of angle RKQ, we need to find the measure of angle PRQ. In the big triangle, the sum of angle measures is 180 degrees, and we know two of the angles, 50 deg and 30 deg (for a total of 80 deg). That leave 100 degrees for the measure of angle PRQ.
But RK is an angle bisector, so \(m\angle{KRQ}=50^\circ\).
We now know two of the angles in \(\triangle{KRQ}\), 50 deg and 15 deg. Those total 65 degrees, so \(m\angle{RKQ}=180^\circ - 65^\circ=115^\circ\)
Consider the following data points, where the first coordinate corresponds to x and the second coordinate corresponds to y: (0,0) (1,0) (2,0) (3.2) Observe there is a missing value (?). It is known that the Adjusted r Squared is 0.4 and the mean residual sum of squares is 9.6 Compute the t-statistic used to test the null hypothesis: slope of regression equal to -2 (minus 2). (Enter your answer to two decimal places. For "0.98", you would write 0.98). If your result is negative, introduce the minus sign. Use as many decimals as possible in your intermediate computations.
Answers
The t-statistic is 0 based on regression equation.
To compute the missing value, we need to use the regression equation: y = mx + b. We know that the adjusted r squared is 0.4, so the coefficient of determination is 0.4. This means that 40% of the variation in y can be explained by the variation in x.
We also know that the mean residual sum of squares is 9.6, which is the average of the squared differences between the predicted values and the actual values.
Using these values, we can find the regression equation:
y = mx + b
0.4 =\(slope of regression^2 * variance of x / variance of y\)
Since the variance of x is 1.67 and the variance of y is unknown, we can solve for the slope of regression:
slope of regression = \(\sqrt{(0.4 * variance of y / 1.67) }\)
Next, we can use the slope of regression to find the missing value:
y = mx + b
0 = slope of regression * 0 + b
b = 0
Therefore, the regression equation is:
y = slope of regression * x
Using the remaining data points, we can find the slope of regression:
(0,0) -> (1,0): slope = 0 / 1 = 0
(1,0) -> (2,0): slope = 0 / 1 = 0
(2,0) -> (3,-?): slope = (-?) / 1 = -slope of regression
Since we know that the slope of regression is -2, we can solve for the missing value:
(-?) / 1 = 2
-? = 2
? = -2
Therefore, the missing value is -2.
To find the t-statistic used to test the null hypothesis that the slope of regression is equal to -2, we need to use the following formula:
t = (slope of regression - hypothesized slope of regression) / standard error of slope
The standard error of slope is given by:
SE = \(\sqrt{(mean residual sum of squares / (n - 2) / variance of x) }\)
Using the values given in the problem:
SE = \(\sqrt{(9.6 / (3 - 2) / 1.67)} = \sqrt{(9.6 / 1.67)}\) = 2.57
Therefore, the t-statistic is:
t = (-2 - (-2)) / 2.57 = 0
The t-statistic is 0.
Learn more about regression here:
https://brainly.com/question/30489365
#SPJ11
If the same condition is described as both acute (subacute) and chronic, and separate subentries exist in the Index at the same indentation level, code_____.
Answers
If the same condition is described as both, as separate subentries exist in the Index at the same indentation level, code both the acute/subacute and chronic codes.
When a condition is described as both acute and chronic, and separate subentries for each descriptor exist in the Index, it is appropriate to code both the acute/subacute and chronic codes. This is because the two descriptors refer to different stages or phases of the same condition. For example, a patient may have both acute and chronic bronchitis, with the acute exacerbations superimposed on a chronic underlying condition.
In such cases, it is important to capture both aspects of the condition to ensure accurate documentation and appropriate reimbursement for healthcare services provided. Therefore, coders should consult the guidelines and the Index to Diseases and Injuries to determine which codes are appropriate for reporting.
For more questions like Chronic Code visit the link below:
https://brainly.com/question/30038725
#SPJ11
y=9x -7 in standard form
Answers
Answer:
change to standard form
-9x+y=4
multiply through by -1
9x-y=-4
If profits decrease by 13.8% when the degree of operating
leverage (DOL) is 3.8, then the decrease in sales is:
A) 0.28%
B) 0.52%
C) 3.63%
D) 10%
E) 52.44%
Answers
Given that profits decrease by 13.8% when the degree of operating leverage (DOL) is 3.8.
The decrease in sales is: We have to determine the percentage decrease in sales Let the percentage decrease in sales be x.
Degree of Operating Leverage (DOL) = % change in Profit / % change in Sales3.8
= -13.8% / x Thus, we have: x
= -13.8% / 3.8
= -3.63%Therefore, the decrease in sales is 3.63%.Hence, the correct option is C) 3.63%. Percentage decrease in sales = % change in profit / degree of operating leverage
= 13.8 / 3.8
= 3.63% The percentage decrease in sales is 3.63%.
To know more about profits, visit:
https://brainly.com/question/29987711
#SPJ11
8x27 using distributive property and mental math
Answers
Answer:
216
Step-by-step explanation:
8×20=160 and 8×7=56 160+56=216 idky u told me to do it in my head but i did so ya
Can someone help me please?
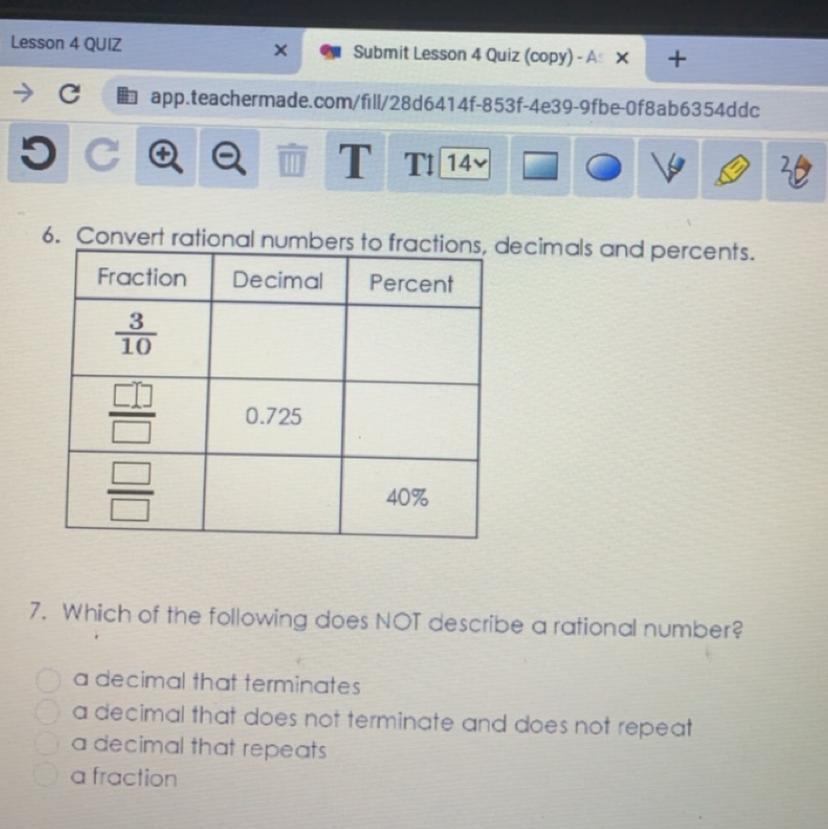
Answers
725/1000=0.725=72.5%
4/10=0.4=40%
Please help me on this!

Answers
Answer:
One solution
Step-by-step explanation:
I added a photo of my solution

Answer:
The system has one solution: (0, 4).
Help me pls! I would love a little help.

Answers
Answer:
i dont know but if u mark me as brainliest i will tell u
'
Step-by-step explanation:
Btw opposite reciprocal just means opposite sign like + to a - and reciprocal means flipping the fraction so I hope this helps
i need help on questions 4, 5, and 6. please help!

Answers
Step-by-step explanation:
4) d = √(3-1)²+(7-(-1))²
=√2²+8² = √4+64 =√68
5) AD=29
AB =2x+4,BC=2x,CD=x
AD = 2x+4+2x+x
29=2x+4+2x+x
29=5x+4
29-4=5x
x=25/5
x=5
AB =2x+4
=2(5)+4 =14
BD = BC +CD
= 2x+x
=2(5)+5 =15
Help plsssssss ,it would mean a lot thankyou

Answers
Answer:
Part 1;
(0, 0)
Part 2;
(0, 2.5)
Step-by-step explanation:
Part 1
The given system of inequalities is presented as follows;
f(x) < x + 4; f(x) > -x - 3; and f(x) < 5
We check each of the points as follows;
The point (0, 0) in the inequality f(x) < x + 4, gives;
f(0) < 0 + 4
f(0) = 0 < (is less than) 0 + 4 = 4
Therefore, (0, 0) is a solution of the inequality f(x) < x + 4
The point (0, 0) in the inequality f(x) > -x - 3, gives;
f(0) < -0 - 3
f(0) = 0 > (is larger than) -0 - 3 = -3
Therefore, (0, 0) is a solution of the inequality f(x) > -x - 3
The point (0, 0) in the inequality f(x) < 5, gives;
f(0) < 5
f(0) = 0 < (is less than) 5
Therefore, (0, 0) is a solution of the inequality f(x) < 5
The point (-6, 0) in the inequality f(x) > -x - 3, gives;
f(-6) = -6 - 3 = 3
The point (-6, 0) with y = 0 < (is less than) f(-6) = 3, therefore (-6, 0) is not a solution to (not included in the graph of) the inequality f(x) > -x - 3 and therefore to the system of inequalities because at x = -6, the values of f(x) > -x - 3 are larger than 3
The point (-3, 4) in the inequality f(x) < x + 4, gives;
f(-3) = -3 + 4 = 1
The point (-3, 4) with y = 4 < (is larger than) f(-2) = 1, therefore (-3, 4) is not a solution to (not included in the graph of) the inequality f(x) < x + 4 and therefore to the system of inequalities because at x = -3, the values of f(x) < x + 4 are less than 1
The point (4, 6) is not a solution to (not included in the graph of) the inequality f(x) < 5 and therefore to the system of inequalities because f(x) is larger than 5 for all x
Therefore, the point which is part of the solution set of the system of inequalities is (0, 0)
Part 2
The given system of inequalities are, f(x) ≥ 2·x + 2; f(x) ≤ -4·x + 3; and f(x) ≤ 6·x + 5
Plotting the given system of inequalities on MS Excel the point which is part of the solution is given by points which are within the triangular intersection area of the three inequalities, with coordinates, (1/6, 7/3), (-3/4, 1/2), and (-1/5, 19/5)
Therefore, the points, (0, 0), (-2.5, 0) are not solutions because, the y-value of the solution area are all higher than the line y = 0
The point (0. 6.5) is not a solution because the points in the triangular solution area all have x-values lesser than x = 6.5
The point which is part of the solution by examination is the point (0, 2.5) which is a point between the lines y = 19/5 = 3.8, y = 1/2, x = -3/4, and x = 1/6.

Identify the equation that describes the line in slope-intercept form.
slope =−1/3, point (−2,3) is on the line
Answers are attached. Please help

Answers
Answer:
1 is the correct option
I think so
The equation describes the line in the slope-intercept form will be y = (1/3)x +(2/3). Option A is correct.
What is the slope?The ratio that y increase as x increases is the slope of a line. The slope of a line reflects how steep it is, but how much y increases as x increases. Anywhere on the line, the slope stays unchanged (the same).
\(\rm m =\dfrac{y_2-y_1}{x_2-x_1}\)
It is given that the slope of the line is −1/3 and passes through the points (−2,3)
A straight line is a combination of endless points joined on both sides of the point. It is shown by the slope-intercept form.
The standard form of the slope-intercept is,
y-y₁ = m(x-x₁)
y-3=−1/3(x-(-2)
y-3=-1/3(x+2)
y = -1/3 x - 2/3 +3
y= -1/3x -7/3.
Thus, the equation describes the line in the slope-intercept form will be y = (1/3)x +(2/3). Option A is correct.
Learn more about the slope here:
brainly.com/question/3605446
#SPJ5
16a² - 2a +4 =-1
Solve equation by quadratic formula
Answers
Answer:
a = (1 -i√79)/16 and a = (1 +i√79)/16
Step-by-step explanation:
You want to solve the quadratic equation 16a² -2a +4 = -1 using the quadratic formula.
Standard formThe equation is written in standard form by adding 1 to both sides:
16a² -2a +5 = 0
The coefficients are (16, -2, 5) and are conventionally given the names (a, b, c). We will use those names in the quadratic formula, trusting you can avoid confusion with the variable name, which is also 'a'.
FormulaThe solution to the equation ax² +bx +c = 0 is given by the formula ...
\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Using this formula, the solutions to the given quadratic are ...
\(a=\dfrac{-(-2)\pm\sqrt{(-2)^2-4\cdot16\cdot5}}{2\cdot16}=\dfrac{2\pm2\sqrt{-79}}{32}=\dfrac{1\pm i\sqrt{79}}{16}\)
The solutions to the equation are ...
a = (1 -i√79)/16 and a = (1 +i√79)/16
Please explain thank you

Answers
In a sample the Upper Specification Limit (USL) is 14 and the Lower Specification Limit (LSL) is 0. The Standard Deviation for the Process is 2. What is Cp, and is the process capable if the goal is 1.33
Answers
The calculated Cp value is 1.17. The goal for this process is a Cp of 1.33. Since the calculated Cp is lower than the desired value, the process is not considered capable of meeting the specified goal. This indicates that there may be a need for process improvement to achieve the desired capability.
Cp is a statistical tool used in Six Sigma methodology to measure the process capability of a manufacturing process. It is calculated by dividing the allowable spread (the difference between the USL and LSL) by six times the standard deviation.
In this case, the USL is 14 and the LSL is 0, which means the allowable spread is 14. The standard deviation is given as 2. So, Cp can be calculated as follows:
\(Cp = (USL - LSL) / (6 x Standard Deviation)\)
Cp = (14 - 0) / (6 x 2)
Cp = 1.17
A Cp value of 1 indicates that the process is barely capable of meeting the specifications. A Cp value of less than 1 indicates that the process is not capable of meeting the specifications. A Cp value greater than 1 indicates that the process is capable of meeting the specifications.
In this case, the goal is to have a Cp value of 1.33, which indicates that the process is capable of meeting the specifications with some margin. However, since the calculated Cp value is only 1.17, it indicates that the process is not capable of meeting the specifications as per the desired goal. Therefore, some improvements in the process are required to achieve the desired goal.
Learn more about Cp here:
https://brainly.com/question/30898643
#SPJ11
The Cp is 1.2
Yes, the process is capable with a goal of 1.33
How to determine the valueWe need to know that Cp measures the process capability with respect to its specification using Upper Specification Limit (USL) and Lower Specification Limit (LSL).
The formula for calculating Cp is represented as;
Cp = USL - LSL/6δ
Such that the parameters are expressed as;
USL is the Upper Specification LimitLSL is Lower Specification Limitδ is the standard deviationNow, substitute the values, we get;
Cp = 14 - 0/6(2)
expand the bracket
Cp = 14/12
Divide the values, we get;
Cp = 1. 2
Learn more about process capability at: https://brainly.com/question/13749302
#SPJ4
