help solve a problem
Answers
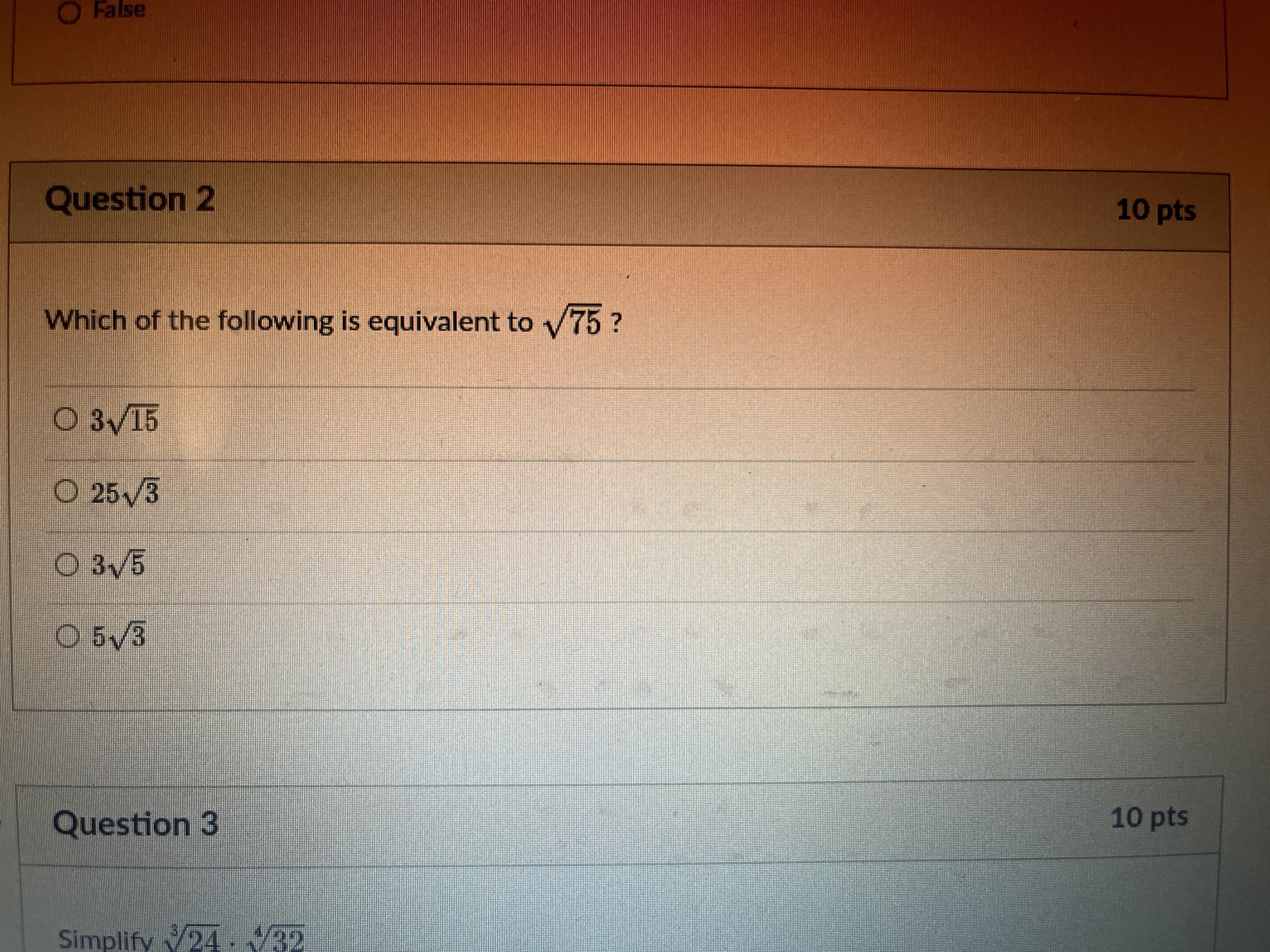
4. factor the following:
\(2x^2-72\)First thing we do is to factor common term 2 as it follows
\(=2(x^2-36)\)then, we factor x^2-36
\(=2\cdot(x-6)\cdot(x+6)\)from the above, we can see that the error was in not multiplying by 2 in the last step
Related Questions
Right triangle EFG has its right angle at F, EG = 6 , and FG = 4 What is the value of the trigonometric ratio of an angle of the triangle? Drag a value to each box to match the trigonometric ratio with its value .

Answers
Answer:
\(\cos G=\dfrac{2}{3}\)
\(\csc E=\dfrac{3}{2}\)
\(\cot G=\dfrac{2}{\sqrt{5}}\)
Step-by-step explanation:
If the right angle of right triangle EFG is ∠F, then EG is the hypotenuse, and EF and FG are the legs of the triangle. (Refer to attached diagram).
Given ΔEFG is a right triangle, and EG = 6 and FG = 4, we can use Pythagoras Theorem to calculate the length of EF.
\(\begin{aligned}EF^2+FG^2&=EG^2\\EF^2+4^2&=6^2\\EF^2+16&=36\\EF^2&=20\\\sqrt{EF^2}&=\sqrt{20}\\EF&=2\sqrt{5}\end{aligned}\)
Therefore:
EF = 2√5FG = 4EG = 6\(\hrulefill\)
To find cos G, use the cosine trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=\dfrac{A}{H}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle G, the adjacent side is FG and the hypotenuse is EG.
Therefore:
\(\cos G=\dfrac{FG}{EG}=\dfrac{4}{6}=\dfrac{2}{3}\)
\(\hrulefill\)
To find csc E, use the cosecant trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cosecant trigonometric ratio} \\\\$\sf \csc(\theta)=\dfrac{H}{O}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle E, the hypotenuse is EG and the opposite side is FG.
Therefore:
\(\csc E=\dfrac{EG}{FG}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\hrulefill\)
To find cot G, use the cotangent trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cotangent trigonometric ratio} \\\\$\sf \cot(\theta)=\dfrac{A}{O}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle G, the adjacent side is FG and the opposite side is EF.
Therefore:
\(\cot G=\dfrac{FG}{EF}=\dfrac{4}{2\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

According to the propertyWhich choice is equivalent to the quotient below!

Answers
Answer:
A
Step-by-step explanation:
Because square root of 30 is 5.4 rounded, and square root of 6 is 2.4 rounded, so 5.4 divided 2.4 is 2.25, and square root of 5 (Answer choice A) is 2.25 rounded as well. They are more accurate when not rounded btw u can check yourself:) HAVE A GREAT DAY/NIGHTT!
The plot below shows the amount of time Mira spent on
5
55 math problems.
All measurements are rounded to the nearest
1
4
4
1
start fraction, 1, divided by, 4, end fraction minute.
A line plot labeled Time per problem (minutes) shows, moving left to right, labeled tick marks at seven, seven and a half, eight, eight and a half, nine, nine and a half, and ten. An unlabeled tick mark appears between each labeled tick mark. Dots are plotted as follows: 2 dots above the unlabeled tick mark between eight and eight and a half and 3 dots above nine and a half.
A line plot labeled Time per problem (minutes) shows, moving left to right, labeled tick marks at seven, seven and a half, eight, eight and a half, nine, nine and a half, and ten.
If Mira had spent the same total amount of time, but spent an equal amount of time on each problem, how many minutes would each problem have taken?
Answers
If Mira had spent the same total amount of time but an equal amount of time on each problem, each problem would have taken around 2.36 minutes.
In the given plot, Mira spent varying amounts of time on each of the 55 math problems. To find out how many minutes each problem would have taken if Mira had spent an equal amount of time on each problem, we need to calculate the total time she spent and divide it by the number of problems.
Looking at the plot, we can estimate the total time Mira spent by counting the dots above each tick mark and multiplying them by the corresponding time interval. Let's break it down step by step:
The tick marks on the plot are at 7, 7.5, 8, 8.5, 9, 9.5, and 10 minutes per problem.
There are 2 dots above the unlabeled tick mark between 8 and 8.5 minutes per problem. We can assume it represents 8.25 minutes.
There are 3 dots above the 9.5 minutes per problem tick mark.
Now, let's calculate the total time Mira spent:
(7 * 2) + (7.5 * 2) + (8 * 2) + (8.25 * 2) + (9 * 2) + (9.5 * 3) + (10 * 2) = 129.5 minutes.
Since Mira spent a total of 129.5 minutes on 55 problems, each problem would have taken approximately 2.36 minutes (rounded to two decimal places) if she had spent an equal amount of time on each problem.
for more such questions on amount
https://brainly.com/question/843074
#SPJ8
What is −30y − 15 if y is 7? (I NEED THIS ASAP)
A: −225
B: −195
C: −52
D: −36
Answers
Answer:
-225
Step-by-step explanation:
-30(7)-15
-210-15
-225
Use differences to find a pattern in the sequence.
3,8,15,28,51,88,143
Assuming that the pattern continues, the eighth term should be
Answers
Answer:
220
Step-by-step explanation:
You want to use differences to find the pattern and the next term in the sequence 3, 8, 15, 28, 51, 88, 143.
First differencesSubtracting each term from the next, we find the sequence of first differences to be ...
5, 7, 13, 23, 37, 55
Second differencesThe first differences are not constant, so we know the sequence is not linear. They are not in an arithmetic progression, so we know the sequence is not quadratic. They do not have a common ratio, so we know the sequence is not exponential.
The second differences are the differences of the sequence of first differences. They are ...
2, 6, 10, 14, 18
Third differencesThe differences of the terms of the 2nd-difference sequence are constant: 4.
4, 4, 4, 4, 4
Constant 3rd differences mean the original sequence can be described by a 3rd degree polynomial. The coefficients found by a calculator are shown in the attachment.
Next termSince we know the third differences are constant, we can work our way back up the chain of differences to find the next term of the original sequence.
next 2nd difference = 18 +4 = 22
next 1st difference = 55 +22 = 77
next sequence term = 143 +77 = 220
The eighth term should be 220.
__
Additional comment
The n-th term is ...
f(n) = 2/3n^3 -3n^2 +28/3n -4

The function g is related to one of the parent functions
g(x) = x^2 – 3
The parent function is:
f(x)= x^2
Use function notation to write g in terms of f.
Answers
We can write g in terms of f as: g(x) = f(x) - 3 = x² - 3
What is function?
In mathematics, a function is a relationship between two sets of elements, called the domain and the range, such that each element in the domain is associated with a unique element in the range. In simpler terms, a function is a set of rules that takes an input value and produces a corresponding output value.
To write g in terms of f, we can use function composition, which involves plugging the function f(x) into g(x) wherever we see x.
So, we have:
g(x) = f(x) - 3
where f(x) = x².
Substituting f(x) into g(x), we get:
g(x) = (x²) - 3
Therefore, we can write g in terms of f as:
g(x) = f(x) - 3 = x² - 3.
To learn more about functions from the given link:
https://brainly.com/question/12431044
#SPJ1
please answer this !!!

Answers
How do you find the volume of a pyramid height 10 length 8 width 6?
Answers
Answer:
just multiply everything together, to get volume.
Answer:
The general volume of a pyramid formula is given as: Volume of a pyramid = 1/3 x base area x height.
Step-by-step explanation:
What is the amplitude of the sinusoidal function
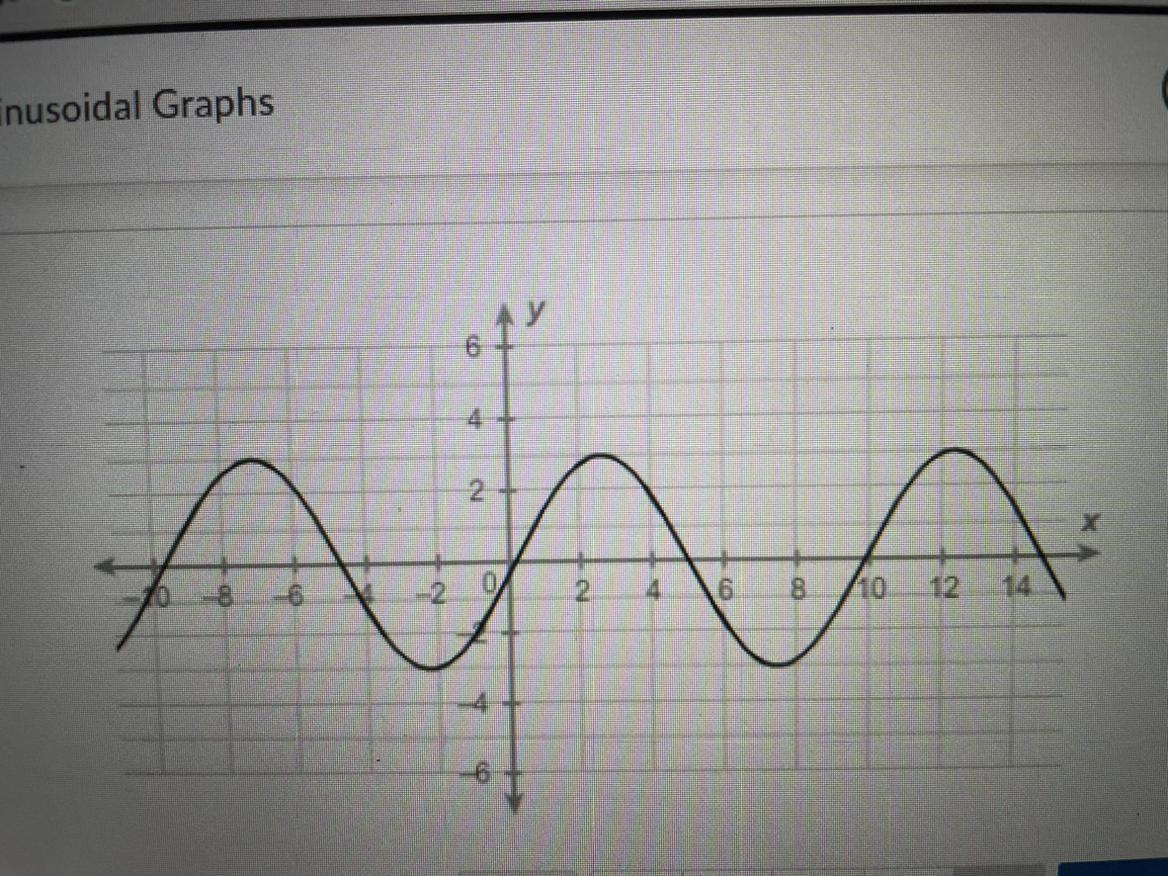
Answers
Answer: 3
Step-by-step explanation:
The vertical distance between the sinusoidal axis and the maximum or minimum value of the function.
Trust
The question is present in the image
Answers

It is the last one ...................
Select the correct answer.
Which statement correctly compares the graph of function g with the graph of function ??
FE) = e²-
g(x) = ² - 4
O A.
OB.
O C.
O D.
The graph of function g is a horizontal shift of the graph of function to the right.
The graph of function g is a vertical stretch of the graph of function f.
The graph of function g is a vertical compression of the graph of function f.
The graph of function g is a horizontal shift of the graph of function f to the left.
Reset
Next

Answers
A statement that correctly compares the graph of function g with the graph of function f include the following: C. The graph of function g is a vertical compression of the graph of function f.
What is a dilation?In Mathematics and Geometry, a dilation is a type of transformation which typically transforms the dimension (size) or side lengths of a geometric object, without affecting its shape.
Therefore, the dimension or side lengths of the dilated geometric object would be stretched or compressed (shrunk) depending on the scale factor that is applied.
When the parent function \(f(x) = e^x -4\) is vertically compressed by a scale factor of 1/2, the transformed function g(x) is given by the following equation;
g(x) = kf(x)
g(x) = 1/2f(x)
\(g(x) = \frac{1}{2} e^x -4\)
Read more on dilation and scale factor here: brainly.com/question/4421026
#SPJ1
Find the number of sides for a regular polygon whose interior angles each measure 10 times each exterior angle
Answers
Answer:
22 sides
Step-by-step explanation:
The expression to find an interior angle of a polygon is:
\(\frac{(n-2)*180}{n}\)
The expression to find an exterior angle of a polygon is:
\(\frac{360}{n}\)
Please note that "n" represents the number of sides the polygon has.
We can use these two expressions to set up an equation.
\(\frac{(n-2)*180}{n}=10(\frac{360}{n})\)
Multiply both sides by "n":
\((n-2)*180=10n(\frac{360}{n})\)
Now, distribute:
\(180(n)-180(2)=\frac{3600n}{n}\\180n-360=3600\)
Divide both sides by 10:
\(\frac{180n}{10}-\frac{360}{10}=\frac{3600}{10}\\\)
\(18n-36=360\)
Add 36 to both sides:
\(18n=360+36\\18n=396\)
Divide both sides by 18:
\(n=22\)
The polygon has 22 sides
At a football stadium, 4% of the fans in attendance were teenagers. If there were 260 teenagers at the football stadium, what was the total number of people at the stadium?
Answers
Answer:
solution
4%=260
100%=?
=(100x260)/4
=6500
Percentage of fans in the stadium who were teenagers = 4%
Number of teenagers in the match = 260
Let the total number of people at the stadium be x.
Which means :
\( =\tt 4\% \: \: of \: \: x = 260\)
\( =\tt \frac{4}{100} \times x = 260\)
\( =\tt \frac{4 \times x}{100} = 260 \)
\( = \tt \frac{4x}{100} = 260\)
\( = \tt4x = 260 \times 100 \\ \tt \: \: \: = 26000\)
\( =\tt x = \frac{26000}{4} \)
\(\color{plum} =\tt x = 6500\)
▪︎Therefore, number of people at the stadium = 6500
Ricky ran 3/4 of a mile in 1/12 of an hour. What was Ricky´s average speed?
Answers
Answer: 9
Step-by-step explanation:
3/4mile takes 1/12 hours
so a whole hour is 3/4 / 1/12 = 3/4*12 = 9miles/hour
Answer:
3/2 miles per hour
Step-by-step explanation:
To find his average speed, divide 3/4 mile by 1/2 hour:
3 2
----- * ------ = 3/2 miles per hour
4 1
What is the area of FGH? (Please help it’s due tmrw !! I’ll mark you brainliest)

Answers
Answer:
102.0625 square units
Step-by-step explanation:
First determine the length of each side using the distance formula for two points. Then use Heron's formula to determine the area of a triangle given three sides
Distance Formula
The distance between two points is the length of the path connecting them
The distance between points (x₁, y₁) and (x₂, y₂) is given by the Pythagorean theorem:
\(d = \sqrt {(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2}\)
Let's compute the lengths of the sides FH, FG and HG
The three vertices are F(-2, 5) G(7, -10) and H(-9, -6) as indicated on the graph
So length FG between (-2,5) and (7,-10)
\(FG= \sqrt {(7 - (-2))^2 + (-10 - 5)^2}\)
\(= \sqrt {(9)^2 + (-15)^2}\)
\(= \sqrt {{81} + {225}}\)
\(= \sqrt {306}\)
FG \(= 17.492856\) (round to 17.5)
Length FH between(-2,5) and (-9, -6) is
\(FH = \sqrt {(-9 - (-2))^2 + (-6 - 5)^2}\)
\(= \sqrt {(-7)^2 + (-11)^2}\)
\(= \sqrt {{49} + {121}}\)
\(= \sqrt {170}\)
FH \(= 13.038405\) (can be rounded to 13.04
Length GH between (7, -10) and (-9, -6) is
\(GH = \sqrt {(-9 - 7)^2 + (-6 - (-10))^2}\)
\(= \sqrt {(-16)^2 + (4)^2}\)
\(= \sqrt {{256} + {16}}\)
\(= \sqrt {272}\)
GH \(= 16.492423\) (can be rounded to 16.5)
Determining the area of a triangle given 3 sides
Heron's formula allows us to find the area of a triangle given 3 sides If the sides are a, b and c the general form of Heron's formula is
\(Area = \sqrt {s(s-a)(s-b)(s-c)}\)
where s is the semi-perimeter = \(\frac{a+b+c}{2}\)
Substituting values we get
s = \(\frac{17.5+13.04+16.5}{2} = 23.52\)
\(Area = \sqrt {23.52(23.52-17.5)(23.52-13.04)(23.52-16.5)}\)
\(= \sqrt{23.52\cdot6.02\cdot10.48\cdot7.02}\)
\(102.0625\) square units
What is the difference of the fractions? Use the number line and equivalent fractions to help find the answer.
다.
1
-2
-2
1
-1
7
0
2
X
tiw b
- یہ

Answers
9514 1404 393
Answer:
(c) -3/4
Step-by-step explanation:
Subtracting a positive number moves you to the left on the number line. Subtracting a negative number moves you in the opposite direction, to the right.
Here, we start at -2 1/2 = -5/2, and we move 1 3/4 = 7/4 to the right from there. Each mark on this number line is 1/4 unit, so we move 7 marks. The results is ...
-2 1/2 -(-1 3/4) = -5/2 +7/4
= -10/4 +7/4 = -3/4

What are four consecutive even integers if the first integer is −4? Responses
A) -4,-3,-2,-1
b) -4,-2,0,2
c) -4,-6,-8,-10
D)-4,-5,-6,-7
Answers
The asked consecutive even integers are -4,-2,0,2
What are consecutive integers?Consecutive integers are whole numbers that follow each other without gaps. For example, 15, 16, 17 are consecutive integers.
Given that, what are four consecutive even integers if the first integer is −4
We know that, Consecutive even integers are even integers that follow each other, and they differ by 2. If x is an even integer, then x + 2, x + 4 and x + 6 are consecutive even integers.
Therefore, here x = -4,
-4+2 = -2
-4+4 = 0
-4+6 = 2
Hence, the asked consecutive even integers are -4,-2,0,2
Learn more about Consecutive integers, click;
https://brainly.com/question/1767889
#SPJ1
- Suppose y varies directly as x. If y = -7 when x = -14, find y when x=3
Answers
Answer:1.5
Step-by-step explanation:
Y=1/2 of x
Jordyn's rectangular garden is represented in the diagram below. If a diagonal walkway crosses their garden, what is its length, in feet?
Walkway
8 feet
15 feet
Answers
Answer: 23
Step-by-step explanation:
Freya earns $1575 per month. What is the maximum amount she should budget for
housing?
Answers
Freya should budget a maximum of $472.50 for housing expenses based on the guideline of spending 30% of her monthly income.
When budgeting for housing, it is generally recommended to allocate a certain percentage of your income towards housing expenses. The recommended percentage varies depending on factors such as location, personal financial goals, and individual circumstances.
A common guideline is to spend no more than 30% of your monthly income on housing expenses. To determine the maximum amount Freya should budget for housing, we can calculate 30% of her monthly income:
Maximum housing budget = 30% of $1575
Maximum housing budget = 0.30 × $1575
Maximum housing budget = $472.50
Therefore, Freya should budget a maximum of $472.50 for housing expenses based on the guideline of spending 30% of her monthly income.
for such more question on income
https://brainly.com/question/15169974
#SPJ8
A cylinder has a height of 20 cm and a diameter of
6 cm. What is the volume, in cubic centimeters, of the
cylinder? Use 3.14 for T.
Answers

Please hurry. It’s due in 20 minutes

Answers
Answer:
root(x+6) +3
Step-by-step explanation:
so you see that it is moved 2 left and 5 up
so root (x+6) +3
If trapezoid JKLM is translated using the rule (x, y) → (x + 3, y − 3) and then translated using the rule (x, y) → (x − 1, y + 1) to create trapezoid J″K″L″M″, what is the location of L″?

Answers
The location of L″ is (-5, 0).
To find the location of L″, we first need to apply the first translation rule to the coordinates of trapezoid JKLM:
J': (x, y) → (x + 3, y - 3) => J'(-2+3, 1-3) = J(1, -2)
K': (x, y) → (x + 3, y - 3) => K'(1+3, 1-3) = K(4, -2)
L': (x, y) → (x + 3, y - 3) => L'(3+3, -2-3) = L(6, -5)
M': (x, y) → (x + 3, y - 3) => M'(-4+3, 2-3) = M(-1, -1)
Now, we need to apply the second translation rule to the coordinates of J', K', L', and M':
J'': (x, y) → (x - 1, y + 1) => J''(1-1, -2+1) = J''(0, -1)
K'': (x, y) → (x - 1, y + 1) => K''(4-1, -2+1) = K''(3, -1)
L'': (x, y) → (x - 1, y + 1) => L''(6-1, -5+1) = L''(5, -4)
M'': (x, y) → (x - 1, y + 1) => M''(-1-1, -1+1) = M''(-2, 0)
Therefore, the location of L″ is (-5, 0).
Learn more about Transformation here:
https://brainly.com/question/13801312
#SPJ1
Answer:
(5,-4)
Step-by-step explanation:
What are the coordinates of the midpoint of AB? If B is (7,-5) and A is (2,8)
(4 1/2, 1 1/2)
(5,0)
(4 1/2, 1)
(4 1/2, 2)

Answers
Answer:
(4 1/2 , 1 1/2)
Step-by-step explanation:
to find midpoint follow the formula (x1 +x2/2 , y1+y2/2)
so (2+7/2 , 8 + -5/2)
(9/2 , 3/2)
(4.5 , 1.5)
which equations are true for x = –2 and x = 2? Select two options x2 – 4 = 0 x2 = –4 3x2 + 12 = 0 4x2 = 16 2(x – 2)2 = 0
Answers
Answer:
x2-4=0 and 4x 2 = 16
QUESTION 5
A basketball player scores 126 points in 7 games. At this rate how many points will he score in a 32 game season?
Answers
what are the importance of statistics in estate management?
Answers
1. Given the derivative of f, use sign chart to determine the interval(s) where f is increasing/decreasing.
f′(x)=(x+3)(3x−1)(x−2)
2. The function f(x) = 2x3 + 9x2 -60x + 70 has a local maximum at x=___ and a local min at x=___
3. Find the second derivative of f(x) = 2x3 + 9x2 -60x + 70 and its sign chart. Which of the following is true about f?
a. f is concave up for x>3/2; concave down for x<3/2; inflection point at x=3/2
b. f is concave up for x>2; concave down for x<-5; inflection point at x=0
c. f is concave up for x>-2; concave down for x<5; inflection point at x=0
d. f is concave up for x>-3/2; concave down for x<-3/2; inflection point at x=-3/2
Answers
The second derivative of f(x) = 2x3 + 9x2 -60x + 70 is f''(x) = 6x2 + 18x - 60, and its sign chart shows that f is concave up for x> -3/2; concave down for x< -3/2; inflection point at x=-3/2, option d is true, and f is concave up for x> -3/2; concave down for x< -3/2; inflection point at x=-3/2.
The second derivative of \(f(x) = 2x3 + 9x2 -60x + 70 is f''(x) = 6x2 + 18x - 60.\) This means that the sign chart for f''(x) is + for x> -10/3, 0 for x= -10/3 and - for x< -10/3. This means that the function is concave up for x> -10/3, concave down for x< -10/3, and has an inflection point at x = -10/3. This means that option d is true, and f is concave up for x> -3/2; concave down for x< -3/2; inflection point at x=-3/2.
To determine this, we need to calculate the second derivative of f(x). The derivative of a polynomial is calculated using the power rule, which states that the derivative of f(x) = axn is f'(x) = anxn-1. Therefore, the second derivative of f(x) = 2x3 + 9x2 -60x + 70 is f''(x) = 6x2 + 18x - 60. We can then plot a sign chart of the second derivative, which will show us the intervals where the function is increasing or decreasing. For f''(x), the sign chart is + for x> -10/3, 0 for x= -10/3 and - for x< -10/3. This means that the function is concave up for x> -10/3, concave down for x< -10/3, and has an inflection point at x = -10/3, which is the same as saying that f is concave up for x> -3/2; concave down for x< -3/2; inflection point at x=-3/2.
The second derivative of f(x) = 2x3 + 9x2 -60x + 70 is f''(x) = 6x2 + 18x - 60, and its sign chart shows that f is concave up for x> -3/2; concave down for x< -3/2; inflection point at x=-3/2.
Learn more about second derivative here:
https://brainly.com/question/29090070
#SPJ4
The functions and are defined as follows.
r(x)= -x+1
s(x)= x^2+2
Find the value of r(s(5))
Answers
Answer: \(r(s(5))=-26\)
Step-by-step explanation:
\(s(5)=5^2 +2=27\\\\r(s(5))=r(27)=-27+1=-26\)
Solve for x and show steps . Is the solution extraneous ? Check your work to show how you determined if the solution is extraneous or not
Square 4x-3=5
Answers
The solution of the equation 4x - 3 = 5 is not extraneous .
How to solve an equation?Extraneous solutions are values that we get when solving equations that aren't really solutions to the equation.
Therefore, let's solve the equation to know whether it is extraneous solution.
Hence,
4x - 3 = 5
add 3 to both sides of the equation
4x - 3 + 3 = 5 + 3
4x = 8
divide both sides of the equation by 4
4x / 4 = 8 / 4
x = 2
Therefore, it is not extraneous solution.
learn more on equation here: https://brainly.com/question/29135995
#SPJ1