hey everyone! can u guys please help i really struggle in math and i just need some help
i will follow and mark u as brainleist even if u know a friend or google that could help me
thanks everyone and have a great corona time day

Answers
Answer:
d= 5.2
[][][]-[][][]
P = √5.2 ^3
P = √5.2 × 5.2 × 5.2
P = √140.608 (plug into calculator)
P = 11.857824421
P = 11.86
The orbital period of Jupiter is 11.86 Earth years.
Related Questions
Mark makes a pattern that starts with 5 and uses the rule “subtract 1, and then multiply by 3.”
Answers
Answer:
12
Step-by-step explanation:
(5 - 1) X 3
4 x 3
12
Have an amazing day!
PLEASE RATE AND MARK BRAINLIEST!!!
1. Solve n3 = 27. Please :(
Answers
Answer:
3
Step-by-step explanation:
Don't know how to explain it I just know that 27 has a perfect cube of 3.
Answer:
n = 9
Step-by-step explanation:
n3 = 27
n3/3 = 27/3
n = 9
Announcements for 84 upcoming engineering conferences were randomly picked from a stack of IEEE Spectrum magazines. The mean length of the conferences was 3.94 days, with a standard deviation of 1.28 days. Assume the underlying population is normal.
a. In words, define the random variables X and .
b. Which distribution should you use for this problem? Explain your choice.
c. Construct a 95% confidence interval for the population mean length of engineering conferences.
i. State the confidence interval.
ii. Sketch the graph.
iii. Calculate the error bound.
Answers
The random variable X represents the length of each engineering conference, and is measured in days.
The normal distribution should be used for this problem, as the underlying population is normal. The normal distribution is a continuous probability distribution that is characterized by a symmetric bell-shaped curve. It is a useful model for events that follow a normal or Gaussian pattern, such as the lengths of engineering conferences.
c. i. The 95% confidence interval for the population mean length of engineering conferences is (3.38, 4.50) days.
ii. The graph of the 95% confidence interval for the population mean length of engineering conferences is shown below.
iii. The error bound for the 95% confidence interval is 0.77 days. This can be calculated using the formula: Error Bound = 1.96*(standard deviation/√sample size). In this case, the error bound is calculated as: 1.96 * (1.28/√84) = 0.77.
Learn more about normal distribution here:
https://brainly.com/question/29509087
#SPJ4
Write a function g whose graph represents a reflection in the x-axis of the graph of f(x)=1/2x-3
Answers
Answer: g(x) = -(1/2)*x + 3.
Step-by-step explanation:
First, let's define a reflection over the x-axis.
If we have a point (x, y) and we reflect it over the x-axis, our new point will be (x, -y).
Now, when we have a function
f(x) = y, the points can be written as:
(x, y = f(x) ) = (x, f(x))
Then, after the reflection over the x-axis, we have:
(x, y = g(x)) = (x, -f(x))
So now we have g(x) = -f(x)
and we know that f(x) = (1/2)*x - 3
then our new function is g(x) = y = -f(x) = -( (1/2)*x - 3) = -(1/2)*x + 3.
g(x) = -(1/2)*x + 3.
A rectangle has a length of x inches and a width 2 inches less than the length.If the dimensions were doubled, what would be the area, in square inches, of the new rectangle in terms of x?2x−42 x − 48x−88 x − 82x2−4x2 x 2 − 4 x4x2−8x4 x 2 − 8 x
Answers
If the dimensions of the rectangle were doubled, the area in square inches is: \(Area = 4x^2 - 8x\)
Let the length of the rectangle be L.Let the width of the rectangle be W.Given the following data:
Length = x inchesWidth = x - 2 inchesIf the dimensions of the rectangle were doubled, the value of L and W becomes;
\(L = 2x\)
\(W = 2(x - 2)\)
Mathematically, the area of a rectangle is given by the formula;
\(Area = Length\) × \(Width\)
\(Area = 2x\) × \(2(x-2)\)
\(Area = 2x\) × \(2x - 4\)
\(Area = 4x^2 - 8x\) square inches.
Find more information: brainly.com/question/897975
Do you know this?
❤️You are beautiful❤️
You are handsome
You are special
You are great
You are kind
You are cute
You are the best
Thanks for living
Thanks for the memories
Thanks for your happiness
Thanks for being happy
Thanks for being honest
Please live for me
Please love yourself for me
⚡️Please be happy for me⚡️
✨Please be safe for me✨
EVERYTHING'S GONNA BE ALRIGHT. YOU'RE DOING GREAT!
Answers
FOR EACH SITUATION IDENTIFY IT AS AN EXPONENTIAL GROWTH OR EXPONENTIAL DECAY. town's population was 3800 in 2005 and growing at a rate of 2% every year.
Answers
The function of the town's population is an exponential growth
How to classify the function as growth or decayFrom the question, we have the following parameters that can be used in our computation:
Initial population = 3800
Growth rate = 2% every year
From the above, we understand that
There is a growth in the population by 2% every year
Using the above as a guide, we have the following:
This means that the function is an exponential growth
Read more about exponential functions at
https://brainly.com/question/2456547
#SPJ1
The sixth-graders at Barbara's school got to choose between a field trip to a museum and a field trip to a factory. 39 sixth-graders picked the museum and 26 sixth-graders picked the factory. What percentage of the sixth-graders picked the museum
Answers
Answer: 60%
Step-by-step explanation:
Sixth-graders that picked the museum = 39
Sixth-graders that picked the factory = 26
Total number of sixth graders = 39 + 26 = 65
Therefore, the percentage of the sixth-graders that picked the museum would be:
= Sixth-graders that picked the museum / Total number of sixth graders × 100
= 39/65 × 100
= 60%
A water truck is filling a swimming pool. The equation that represents this relationship is y = 19.75x where y is the number of gallons of water in the pool and x is the number of minutes the truck has been filling the pool. Choose True or False for each statement.
Answers
Answer:
The answer is TrueStep-by-step explanation:
Given the expression
y = 19.75x------------------1
and y is the number of gallons
we know that
rate= quantity/time
quantity= rate*time-----------2
comparing the two equations
we can see that
the rate is 19.75 gallons/minutes
and the time is x
therefore x is the number of minutes taken
Halona walks 1. 931. 93 kilometers to a neighbor's house in 2323 minutes. Assuming she walks at a constant speed, write a proportion that represents how many kilometers, yy, halona can walk in xx minutes. Then solve your proportion for yy.
Answers
The required proportional ratio is y = 0.08 x. gives Halona 23 minutes to move her 1.93 kilometers to her neighbor's house. As long as you move at a steady pace.
How many kilometers Halona can run in x minutes y expressed as a ratio. Then find y in percentage. The relationship between two or more proportional or inversely proportional sets of values, whether they are directly related or not, is called proportionality.
Here we have
yxxy = kxwhere k is the proportionality constant ofand at x = 23 y = 1.931.93 = 23k4 k = 2 444k = 1.93k = 0.08Substitute k into the proportional equation.
https//brainly.com/question/22620356
#SPJ4
helppp
britney has already run 10 miles on her own, and she expects to run 3 miles during each track practice. how many track practices would it take for britney to run 40 miles
Answers
Answer:
It would take her 10 track practices to get up to 40 miles.
Step-by-step explanation:
Margaret is building storage boxes. each box will have a length of 8 feet, a width of 512 feet, and a height of 412 feet. a pint of paint covers 50 square feet. how many pints of paint does margaret need to buy in order to paint 3 boxes? 7 pints 10 pints 12 pints 13 pints
Answers
The surface area of a cuboid is the area of all the six faces of a cuboid. The Paint that is required to paint 3 boxes is 13 pints.
What is the surface area of a cuboid?The surface area of a cuboid is the area of all the six faces of a cuboid. It is given by the formula,
\(\rm \text{Surface area of the box}= 2[(Length \times width)+(Width \times Height)+(Length \times height)]\)
As it is given the dimensions of the storage box are a length of 8 feet, a width of 5 1/2 feet(5.5 feet), and a height of 4 1/2 feet(4.5 feet). Therefore, the surface area of the box can be written as,
\(\rm \text{Surface area of the box}= 2[(Length \times width)+(Width \times Height)+(Length \times height)]\)
\(\rm \text{Surface area of the box}= 2[(8\times 5.5)+(5.5\times 4.5)+(8 \times 4.5)] = 209.5\ ft^2\)
As it is given that the surface area that can be covered with a pint of paint is 50 square feet, therefore, the paint that will be required to paint 209 square feet is,
\(\text{Paint Required} = \dfrac{\text{Total area that is needed to be paint}}{\text{Area covered in a pint of paint}}\)
\(\rm \text{Paint Required} = \dfrac{209.5}{50} = 4.19\ pints\)
Now, we know that the surface area of the box is 209 square feet, while the paint required to paint a complete box is 4.19, therefore, the paint that will be required to paint 3 boxes will be,
\(\text{Paint required to paint 3 boxes} = 3 \times 4.19 = 12.57 \approx 13\)
Hence, the Paint that is required to paint 3 boxes is 13 pints.
Learn more about Surface Area of Cuboid:
https://brainly.com/question/26403859
Someone help me solve this please ASAP

Answers
The solution of the linear equations will be (-2, 1).
What is the solution to the equation?The distribution of weights to the variables involved that establishes the equilibrium in the calculation is referred to as a result.
A relationship between two or more parameters that, when shown on a graph, produces a linear model. The degree of the variable will be one.
The linear equation is given as,
y = mx + c
Where m is the slope of the line and c is the y-intercept of the line.
The equations are given below.
y = -(5/2)x - 4
y = (1/2)x + 2
The above equations are the equation of the line.
The lines are drawn on the graph. And the lines intersect at (-2, 1).
Thus, the solution of the linear equations will be (-2, 1).
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ1

We want to measure the activity (number of decays per second, a unit known as Becquerel) of a radioactive source so that we can use it to calibrate the equipment of the gamma-ray experiment. We use an electronic counter and a timer to measure the number of decays in a given time interval. In round numbers we obtain 1000 decays in 10 minutes. How long does it take (in seconds) in order to determine the activity with a statistical uncertainty of 2%
Answers
it would take approximately 0.0004 seconds (or 0.4 milliseconds) to determine the activity with a statistical uncertainty of 2%.
To determine the activity with a statistical uncertainty of 2%, we need to calculate the time interval that would provide sufficient data to achieve this level of precision.
The statistical uncertainty is typically expressed as the standard deviation or the relative standard deviation (coefficient of variation). In this case, let's assume the 2% uncertainty refers to the relative standard deviation.
The relative standard deviation (RSD) is calculated as the standard deviation divided by the mean, expressed as a percentage:
RSD = (Standard Deviation / Mean) * 100%
Given that the mean number of decays in 10 minutes is 1000, we can use this information to calculate the standard deviation:
Standard Deviation = (RSD / 100%) * Mean
= (2% / 100%) * 1000
= 0.02 * 1000
= 20
Now, to determine the time interval required to achieve the desired statistical uncertainty, we can use the following formula:
Time Interval = (Standard Deviation / Mean)²
Time Interval = (20 / 1000)²
= 0.02²
= 0.0004
To know more about deviation visit:
brainly.com/question/31835352
#SPJ11
thomas invests $106 in an account that pays 6 percent simple interest. how much money will thomas have at the end of 4 years?
Answers
Answer:
254 dollars.
Step-by-step explanation:
First, we multiply 106 × 0.6 = 63 dollars. Lastly, we just multiply 63 × 4 = 254.
Hope this helps.
Convert the fraction 4/5 to a decimal.
SHOW WORKING.
Answers
Answer:
The answer is 0.8
Step-by-step explanation:
\( \: \: \: \: \: \: 0. 8\\ 5 \sqrt{40} \\ - 40 \\ 0\)
Thus, The answer is 0.8
-TheUnknownScientist 72
Assume that this proportion is true for ALL children (e.g. that this proportion applies to any group of children), and that the remainder of the questions in this section apply to selections from the population of ALL children. b) If 8 children are chosen, the probability that exactly 4 would draw the nickel too small is: c) If 8 children are chosen at random, the probability that at least one would draw the nickel too small is:
Answers
The probability that at least one child would draw the nickel too small is: P(X ≥ 1) = 1 - P(X = 0).
b) To find the probability that exactly 4 children would draw the nickel too small, we can use the binomial probability formula. The formula is: P(X = k) = (nCk) * (p^k) * (q^(n-k)), where n is the number of trials, k is the number of successes, p is the probability of success, and q is the probability of failure.
In this case, n = 8 (as 8 children are chosen), k = 4 (as exactly 4 children drawing the nickel too small), p = 0.15 (as the probability of a child drawing the nickel too small), and q = 1 - p = 1 - 0.15 = 0.85.
So, the probability that exactly 4 children would draw the nickel too small is: P(X = 4) = (8C4) * (0.15^4) * (0.85^(8-4)).
c) To find the probability that at least one child would draw the nickel too small, we can use the complement rule. The probability of at least one success is equal to 1 minus the probability of no success.
The probability of no success (all children drawing the nickel of the right size) is given by: P(X = 0) = (8C0) * (0.15^0) * (0.85^8).
Therefore, the probability that at least one child would draw the nickel too small is: P(X ≥ 1) = 1 - P(X = 0).
to learn more about probability.
https://brainly.com/question/31828911
#SPJ11
15 customers increased by 200 percent
Answers
When given a line such as y + 2 = 1/2 (x + 20), how do I find the slope intercept form?
Answers
Given the equation of the line:
\(y+2=\frac{1}{2}(x+20)\)The slope-intercept form is: y = m * x + b
Where (m) is the slope
So, we will solve the given equation for (y)
\(\begin{gathered} y+2=\frac{1}{2}\cdot x+\frac{1}{2}\cdot20 \\ y+2=\frac{1}{2}x+10 \\ y=\frac{1}{2}x+10-2 \\ \\ y=\frac{1}{2}x+8 \end{gathered}\)so, the answer will be the slope-intercept form:
\(y=\frac{1}{2}x+8\)if i toss a fair coin five times and the outcomes are ttttt, then the probability that tails appears on the next toss is (a) 0.5. (c) greater than 0.5. (e) 1. (b) less than 0.5. (d) 0.
Answers
If there are a total of two probabilities, then the chance of one probability of happening is 0.5, no matter what.
Therefore, A (0.5), is correct.
an experimental design for a paired t test has pairs of identical twins. how many degrees of freedom are there in this t test?
Answers
The degrees of freedom are in a t test. Degrees of freedom refer to the number of values in a statistical calculation that are free to vary. In a paired t test, the degrees of freedom are calculated as the number of pairs minus 1.
In the case of using pairs of identical twins in an experimental design for a paired t test, each twin in the pair would be considered one observation. So if we have N pairs of identical twins, we would have a total of 2N observations. Since each pair of twins is considered one observation in the t test, we would have N pairs of observations. Therefore, the degrees of freedom in this t test would be N - 1.
In summary, for an experimental design using pairs of identical twins in a paired t test, the degrees of freedom would be equal to the number of pairs of twins minus 1. This is because each pair of twins is considered one observation in the t test.
To know more about Degrees of freedom visit:
https://brainly.com/question/31959834
#SPJ11
which of the following is a true statement [-2]<[1][1]<[0][-1]<[-2][1]>[-2]
Answers
Absolute represented by |x| where x is a number means making the numer positive irrespective of its formal state
1) |-2|<|1|
2< 1
The above statement is false
2) |1|<|0|
1<0
The above statement is also false
3) |-1|<|-2|
1<2
The above statement is true
4) |1| > |-2|
1 > 2
The above statement is false too
QUICK!!!HELP!!!!!!!!!!!!!!!!!!

Answers
Using the normal distribution, the probability that a worker selected at random makes between $500 and $550 is: 2.15%.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean mu and standard deviation sigma is given by:
Z = (X - mu)/sigma
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.The mean and the standard deviation are given as follows:
mu = 400, sigma = 50
The probability is the p-value of Z when X = 550 subtracted by the p-value of Z when X = 500, hence:
X = 550:
Z = (X - mu)/sigma
Z = (550 - 400)/50
Z = 3
Z = 3 has a p-value of 0.9987.
X = 500:
Z = (X - mu)/sigma
Z = (500 - 400)/50
Z = 2
Z = 2 has a p-value of 0.9772.
0.9987 - 0.9772 = 0.0215 = 2.15% probability.
More can be learned about the normal distribution at https://brainly.com/question/15181104
#SPJ1
write a fraction to show the value of each 9 in the decimal 0.999. how is the value of the 9 on the left related to the value of the 9 on the right? how is the value of the 9 on the rigth related to the value of the 9in the middle?
Answers
The fractions to show the value of each 9 in the decima 0.999 are 9/10, 9/100, 9/1000.
How to write decimal number in fractionTo write the fraction that shows the value of each 9 in the decimal 0.999, we can use the following method
The digit 9 in the tenths place represents 9/10 or 0.9.
The digit 9 in the hundredths place represents 9/100 or 0.09.
The digit 9 in the thousandths place represents 9/1000 or 0.009.
Thus, the fractions are
0.9 = 9/10
0.09 = 9/100
0.009 = 9/1000
The value of the 9 on the left is related to the value of the 9 in the middle by a factor of 10.
The value of the 9 on the right is related to the value of the 9 in the middle by a factor of 10, so the 9 on the right is one-tenth the value of the 9 in the middle.
Learn more on fraction on https://brainly.com/question/17220365
#SPJ4
A particle moves along the y-axis so that at time t≥0 its position is given by y(t)=t3−6t2+9t. Over the time interval 0
Answers
Therefore, the maximum displacement of the particle is 4 units, and it occurs at time t = 1.
To find the maximum displacement, we need to first determine the particle's velocity and acceleration.
The velocity of the particle is given by the derivative of its position function:
\(v(t) = y'(t) = 3t^2 - 12t + 9\)
The acceleration of the particle is given by the derivative of its velocity function: a(t) = v'(t) = 6t - 12
Now, to find the maximum displacement, we need to find the time at which the particle comes to rest.
This occurs when its velocity is zero:
\(3t^2 - 12t + 9 = 0\)
Simplifying this equation, we get:
\(t^2 - 4t + 3 = 0\)
This quadratic equation factors as:
(t - 1)(t - 3) = 0
So the particle comes to rest at t = 1 or t = 3.
Next, we need to determine whether the particle is at a maximum or minimum at each of these times.
To do this, we look at the sign of the acceleration:
When t = 1, a(1) = 6(1) - 12 = -6, which is negative.
Therefore, the particle is at a maximum at t = 1.
When t = 3, a(3) = 6(3) - 12 = 6, which is positive.
Therefore, the particle is at a minimum at t = 3.
Finally, we need to find the displacement of the particle at each of these times:
\(y(1) = 1^3 - 6(1)^2 + 9(1) = 4\)
\(y(3) = 3^3 - 6(3)^2 + 9(3) = 0.\)
For similar question on displacement.
https://brainly.com/question/1581502
#SPJ11
What is the circumference of a circle with a radius of 86 inches? use 3.14 for PI
Answers
Step-by-step explanation:
\(circumference = 2\pi\: r \: \\ = 2 \times 3.14 \times 86 \\ = 540.08\)
Answer:
540.08
Step-by-step explanation:
a probability distribution of the claim sizes for an auto insurance policy is given in the table below: claim size 20 30 40 50 60 70 80 probability 0.10 0.10 0.10 0.20 0.15 0.10 0.25 what percentage of the claims are within one standard deviation of the mean claim size?
Answers
55% of the claims are within one standard deviation of the mean claim size.
To find the percentage of claims that are within one standard deviation of the mean claim size, we first need to calculate the mean and standard deviation of the distribution.
The mean claim size is:
u = (20 × 0.10) + (30 × 0.10) + (40 × 0.10) + (50 × 0.20) + (60 × 0.15) + (70 × 0.10) + (80 × 0.25) = 54
The variance can be calculated as follows:
s^2 = [\((20-54)^{2}\) × 0.10] + [\((30-54)^{2}\) × 0.10] + [\((40-54)^{2}\) × 0.10] + [\((50-54)^{2}\) × 0.20] + [\((60-54)^{2}\) × 0.15] + [\((70-54)^{2}\) × 0.10] + [\((80-54)^{2}\) × 0.25] = 340
The standard deviation is the square root of the variance:
s = √340 ≈ 18.44
To find the percentage of claims that are within one standard deviation of the mean claim size, we need to find the range of claim sizes that fall within the interval (u - s, u + s).
(u - s) = 54 - 18.44 = 35.56
(u + s) = 54 + 18.44 = 72.44
We can see from the table that the claim sizes 40, 50, 60, and 70 fall within this range, and their probabilities add up to:
0.10 + 0.20 + 0.15 + 0.10 = 0.55
Therefore, 55 percentage of the claims are within one standard deviation of the mean claim size.
To learn more about standard deviation here:
https://brainly.com/question/23907081
#SPJ4
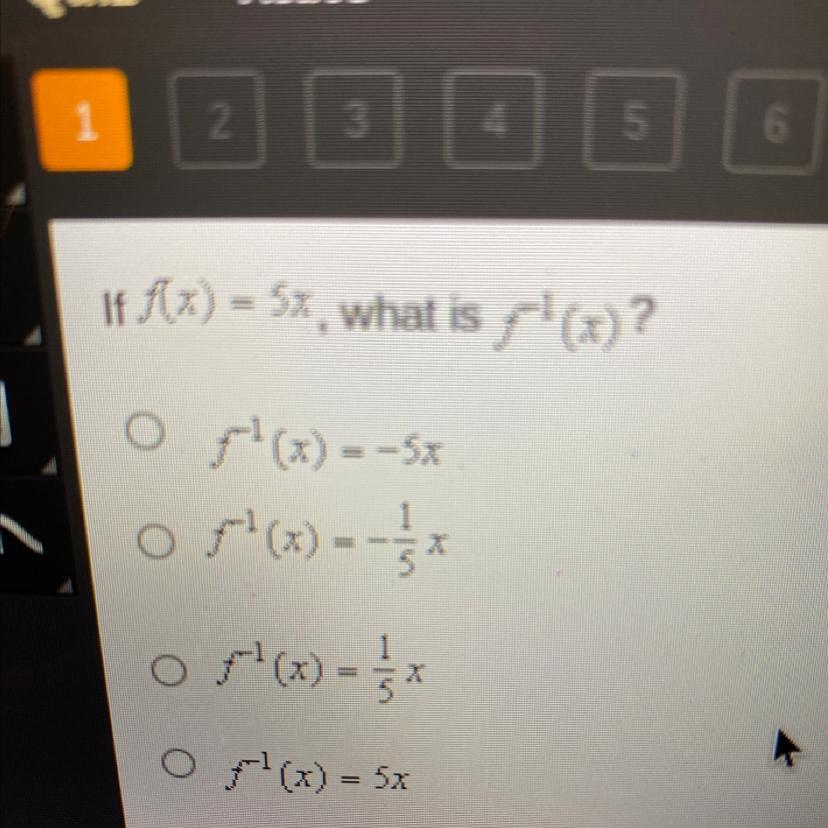
If f(x) = 5x, what is '(x)?
=
OF(x) = -5x
-
o (x) = -5
1=
1
F(
7
1
O x
or?(x) = 5*
Of(x) = 5x
Answers
Answer:
Your answer would be C
Step-by-step explanation:
Trust it's c and if it's not I am sorry but trust me.
here is a sequence of number 7, 5 ,3 ,1, - 1 find the next term in the sequence
Answers
Answer:
-3
Step-by-step explanation:
in every term we subtract 2 so
7-2=5
so in every answer subtract 2
5-2=3
3-2=1
1-2=-1
-1-2=-3
Answer:
- 3
Step-by-step explanation:
There is a common difference between consecutive terms in the sequence, that is
5 - 7 = 3 - 5 = 1 - 3 = - 1 - 1 = - 2
Thus subtracting 2 from the last term shown gives the next term
- 1 - 2 = - 3
a circle passes through the points (2,0) and (8,0) and has the y - axis at a tangent. Find the two possible equations for the circle
Answers
1
2
and has radius 12
1
2
, so the equation is (−12)2+2=12
(
x
−
1
2
)
2
+
y
2
=
1
2
.