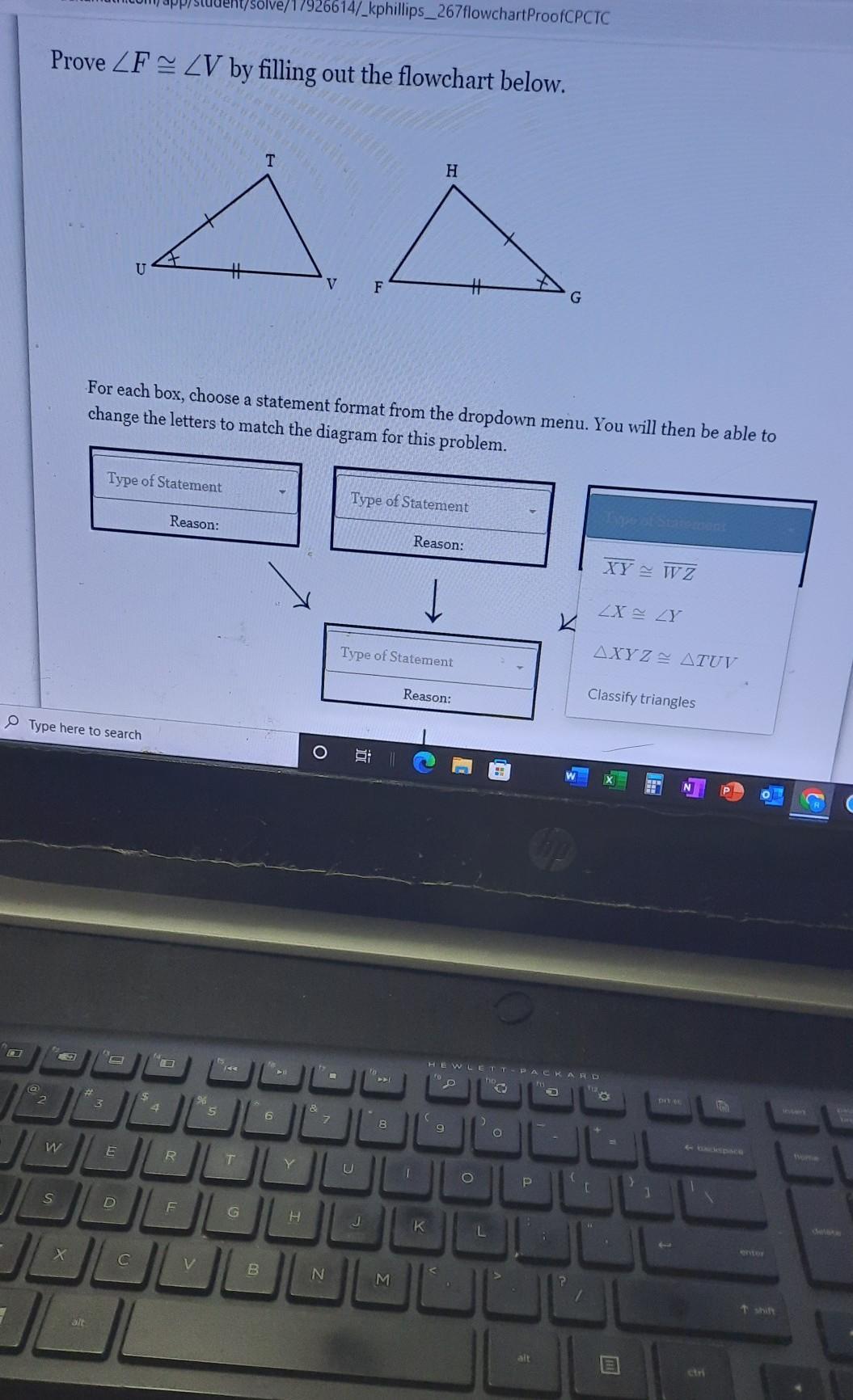
Answers
The two column proof is written as follows
Statement Reason
line UT ≅ line GH given
line UV ≅ line GH given
< U ≅ < G given
Δ TUV ≅ Δ BEC Congruent triangles by SAS
< F ≅ < V CPCTC theorem
What is congruency of triangle?Triangles are said to be congruent when the sides and angles equal in accordance to to the triangle congruency rules
Some of the rules include
Side - Side - Side = SSS
Side - Angle - Side = SAS
Angle - Side - Angle = ASA
Angle - Angle - Side = AAS
Hypotenuse and one leg = HL
The problem requires the prove by Side - Angle - Side = SAS to ensure that the the triangles are congruent
The SAS have it that the two sides of the triangles being compared should be equal and the included angles are equal
The given sides and the included angle are
line UT ≅ line GH Side
< U ≅ < G included angel
line UV ≅ line GH Side
< F ≅ < V CPCTC theorem
According to the CPCTC theorem, whenever two triangles are congruent, then each of their corresponding parts are also congruent. In other words, if two or more triangles are congruent, then their corresponding sides and angles are also congruent or equivalent in size.
Learn more about angles here:
https://brainly.com/question/29393764
#SPJ1
Related Questions
2. The table represents equivalent ratios. What is the missing value of x in the table? (1 point)
xy
8 4
? 3
42
2 1
9
7
6
5
Answers
There is no proportional relationship between x and y.
No, all ratios yx are not equivalent.
We have,
"Two or more number or variable are said to be in proportion if the ratio between them are equivalent to each other."
According to the question,
Given x : 8 , 10, 12, 14
y : 5, 7, 9, 11
Ratio between different values of x and y are not equivalent
( 8 /5) ≠ (10 / 7)≠ (12 /9) ≠(14 /11)
We conclude there is no proportional relationship between x and y.
Hence, Option(1) is the correct answer.
Learn more about Proportion here
brainly.com/question/2548537
#SPJ1
complete question:
Is there a proportional relationship between x and y? Explain.
x 8 10 12 14
y 5 7 9 11
1. No; all ratios yx are not equivalent.
2.Yes; each x value and y value increases by 2.
3.Yes; the difference between each x value and y value is 3.
4.No; all ratios xy are greater than 1.
Correct answer get brainliest!! Determine if the following triangles are congruent if yes state what theorem proves them to be
congruent. Explain your reasoning.

Answers
Answer: AAS
Step-by-step explanation:
We know that \(\angle TSN \cong \angle HSU\) because they are vertical angles, meaning the triangles are congruent by AAS.

What is the slope of line segment E F?
A)1/3
B)3/2
C)2/3
D)-3/2

Answers
Step-by-step explanation:
the picture even tells you the formula.
what ? you cannot do these simple subtractions yourself ? what don't you understand there ? please tell me, so that I can help you with that.
as the formula says, the slope is y difference / x difference between the 2 points.
E = (-2, -4)
F = (2, 2)
for the difference calculation it is just important that you do both in the same direction.
x difference = 2 - -2 = 4
y difference = 2 - -4 = 6
so the slope is 6/4 = 3/2
therefore, B 3/2 is the correct answer
that's it. that is all there was to this.
FYI - the slope indicates how many units y changes, when x changes a certain amount of units when you go from one point on the line to another.
On a test that has a normal distribution, a score of 29 falls three standard deviations above the mean, and a score of 23 falls one standard deviation above the mean. Determine the mean of this test.
Answers
The mean of the test is 20.
To determine the mean of the test, we need to use the information provided about the scores falling above the mean in terms of standard deviations.
Let's denote the mean of the test as μ, and the standard deviation as σ.
We are given that a score of 29 falls three standard deviations above the mean, so we can write this as:
29 = μ + 3σ
Similarly, we are told that a score of 23 falls one standard deviation above the mean, which can be expressed as:
23 = μ + σ
Now we have a system of two equations with two variables (μ and σ). We can solve this system of equations to find the values of μ and σ.
From the second equation, we can isolate μ:
μ = 23 - σ
Substituting this value into the first equation, we have:
29 = (23 - σ) + 3σ
Simplifying the equation, we get:
29 = 23 + 2σ
2σ = 29 - 23
2σ = 6
σ = 3
Substituting the value of σ back into the second equation, we find:
μ = 23 - 3
μ = 20
For more such questions on mean
https://brainly.com/question/29368683
#SPJ8
Given f(x) = (-1)(x) + 2, f(4) is equal to:
Hint: Replace the x in the function with 4.
Answers
Answer:
f(4) = -2
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
FunctionsFunction NotationStep-by-step explanation:
Step 1: Define
f(x) = (-1)(x) + 2
f(4) is x = 4 for function f(x)
Step 2: Evaluate
Substitute in x [Function]: f(4) = (-1)(4) + 2Multiply: f(4) = -4 + 2Add: f(4) = -2Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2
which of the following rotational symmetry is applied to the regular not

Answers
9514 1404 393
Answer:
yesyesStep-by-step explanation:
A regular nonagon has vertices that are 360°/9 = 40° apart. Any rotation by a multiple of 40° will make the figure indistinguishable from the original.
Rotational symmetry of 40° applies.
Rotational symmetry of 200° applies.
Need Help With Math Problem

Answers
each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
A materials engineer wants to test whether or not a certain device spends an average of more than 30 seconds soaking a component part in solution. Therefore, she goes out and takes a simple random sample of n =16 parts, and finds that the sample mean is 33.4 seconds with a sample standard deviation of s =8.0 seconds.
At α= 0.05, the Shapiro-Wilk Test for Normality has a p-value of p = 0.0667.
Suppose the engineer goes back and she selects a 17th sample unit. Using a 95% confidence level, provide the lower end point of a two-tailed interval that would be used to predict the range of values that this 17th sampled unit would be in with respect to seconds soaking a component part in solution.
Answers
Answer:
Using a 95% confidence level, the lower end point of a two-tailed interval that would be used to predict the range of values that this 17th sampled unit would be in with respect to seconds soaking a component part in solution is of 29.137 seconds.
Step-by-step explanation:
We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.
The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So
df = 16 - 1 = 15
95% confidence interval
Now, we have to find a value of T, which is found looking at the t table, with 15 degrees of freedom(y-axis) and a confidence level of \(1 - \frac{1 - 0.95}{2} = 0.975\). So we have T = 2.1315
The margin of error is:
\(M = T\frac{s}{\sqrt{n}} = 2.1315\frac{8}{\sqrt{16}} = 4.263\)
In which s is the standard deviation of the sample and n is the size of the sample.
The lower end of the interval is the sample mean subtracted by M. So it is 33.4 - 4.263 = 29.137 seconds.
Using a 95% confidence level, the lower end point of a two-tailed interval that would be used to predict the range of values that this 17th sampled unit would be in with respect to seconds soaking a component part in solution is of 29.137 seconds.
Measurement of a circle
(Giving brainliest to correct answer)
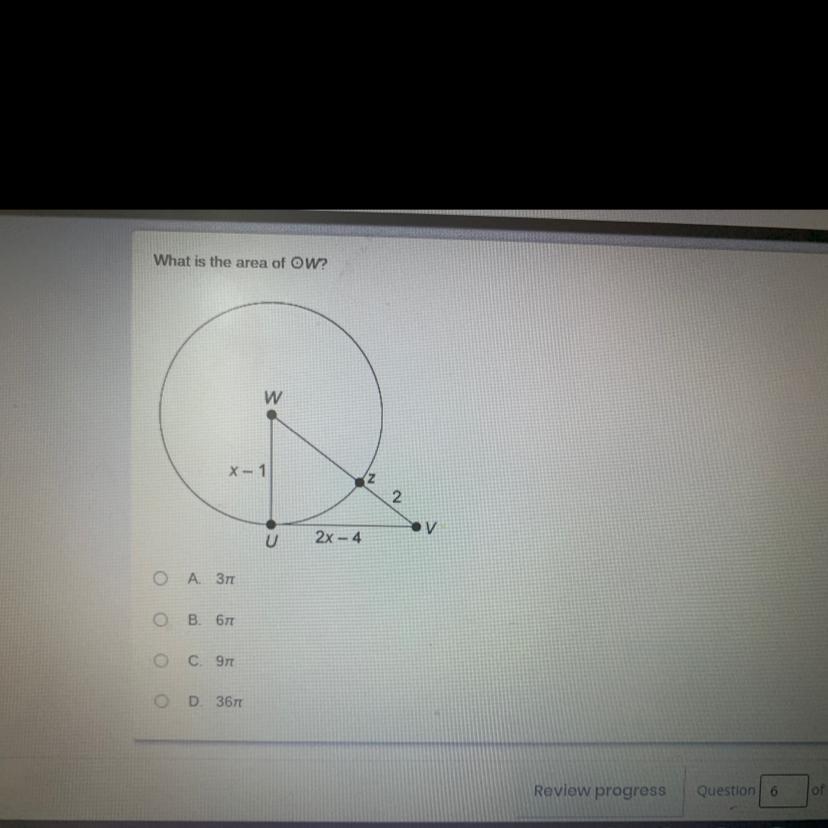
Answers
Answer:
C. \( 9\pi \)
Step-by-step explanation:
VU is tangent \( \odot W\) at point U and WU is radius.
\( \therefore WU \perp VU\)
\( \implies m\angle VUW=90\degree\)
\( \therefore \triangle VUW\) is right angle triangle.
WZ = WU = x - 1 (Radii of same circle)
WV = x - 1 + 2 = x + 1
By Pythagoras Theorem:
\( WU^2 + VU^2 = WV^2 \)
\( (x-1)^2 +(2x-4) ^2 = (x+1)^2 \)
\(x^2 -2x +1+ 4x^2 -16x + 16=x^2 +2x +1\)
\(4x^2 -20x + 16=0\)
\(x^2 -5x + 4=0\)
\(x^2 -5x + 4=0\)
Equating it with
\(ax^2 +bx +c=0\)
We find:
a = 1, b = - 5, c = 4
\( b^2 - 4ac =(-5)^2 - 4(1)(4)= 25-16 =9\)
\( x=\frac{-b\pm \sqrt{b^2 - 4ac}}{2a} \)
\( x=\frac{-(-5)\pm \sqrt{9}}{2\times 1} \)
\( x=\frac{5\pm 3}{2} \)
\( x=\frac{5+3}{2}, \: x =\frac{5-3}{2} \)
\( x=\frac{8}{2}, \: x =\frac{2}{2} \)
\( x=4, \: x =1 \)
When x = 4, radius (r) = 4 - 1 = 3
When x = 1, radius (r) = 1 - 1 = 0, which is not possible.
Area of \( \odot W \)
\( =\pi r^2 \)
\( =\pi (3)^2 \)
\( =9\pi \)
Hai has 24 video games. Six of his games are sports related and the rest are the number of his role-playing games to the total number of games?Hai has 24 video games. Six of his games are sports related and the rest are role-playing games. Which ratio represents the number of his role-playing games to the total number of games?
Answers
The ratio of his role-playing games to all of his other games is 3:4.
What is ratio?An ordered pair of integers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. For instance, you might express the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls) There are 1 in 4 boys and 3 in 4 girls. Ratios contrast two figures by typically dividing them. A/B would be your formula if you were comparing one data point (A) to another data point (B). This indicates that you are multiplying information A by information B. For instance, your ratio will be 5/10 if A is 5 and B is 10.
Here,
If he has 24 video games and 6 are sports games,
24-6=18
The role play games are 18.
Ratio of the number of his role-playing games to the total number of games,
=18/24
=3/4
=3:4
The ratio of the number of his role-playing games to the total number of games is 3:4.
To know more about ratio,
https://brainly.com/question/29467965
#SPJ1
Answer one of the following questions

Answers
Laniqua trains for the long jump each week. She writes this function to model the relationship between
the number of weeks, w , she trains and the distance, f ( w ) , in inches, she can jump.
f ( w ) = 2w + 180
What does the slope of this function represent
Answers
Answer: the number of inches Laniqua’s jump distance increases per week of training
The sum of 12 data values is 942. What is the average of the data values?
Answers
Answer:
To find the average (also known as the arithmetic mean) of the data values, we need to divide the sum of the values by the number of values. We are given the sum of 12 data values, which is 942. So:
Average = Sum of values / Number of values
Average = 942 / 12
We can simplify this by dividing both the numerator and denominator by their greatest common factor, which is 6:
Average = (942 ÷ 6) / (12 ÷ 6)
Average = 157 / 2
Average = 78.5
Therefore, the average of the 12 data values is 78.5.
Step-by-step explanation:
Don has 6 pieces of pipe. Each piece is 2 feet 6 inches long.
If Don joins the pieces end to end to make one long pipe, how long will the new pipe be?
The pipe will be
feet
inches long.
Answers
Answer: 15 feet
Step-by-step explanation:
First you start with 2ft and 6in and convert it all into into inches.
If you know that 1 ft=12in then you know that 2 feet is the same as saying
12+12=24. If you don't understand use this chart-
1 ft=12in
2ft= 24in
3ft= 36in
4ft =48in
5ft= 60in
6ft= 72in
see I am counting by 12's.
Now take 2ft and convert it into inches. That would be 24 in (look in the chart).
now take the 24in(2ft) and add it to the 6in. So 24+6 =30
So now you know that one piece of pipe is 30in long.
But in the text it states that Don has 6 pieces, so...
because it says that he has 6 pieces of pipe then you are going to take that and multiply that number(6) by how long each piece is. look up and it shows how long each pieces is. They are all each 30in long. Take 30 and multiply that by 6 because there are 6 pipes and you will get 120in.
But it says that they need an answer of feet and inches or just feet if it exactly a some sort of foot like 43feet or 2 feet.
So then we are going to convert 180 into feet by dividing 180 by 12 and you get 15. So the answer is 15.
I hope this helps. Have fun learning!!
Answer:
The pipe will be 15 feet 0 inches long.
Step-by-step explanation:
1 pipe is 2 feet 6 inches long
There are 6 pieces
6×2= 12 feet 6×6= 36 inches
The pipe will be 12 feet 36 inches long, however, there are 12 inches in a foot so we can covert the inches to feet
36 inches ÷ 12 inches = 3 feet
12 feet + 3 feet = 15 feet
The pipe will be 15 feet 0 inches long.
Raina drove 464 miles in 8 hours.
At the same rate, how long would it take her to drive 638 miles?
0 hours
X
S
Answers
s= 464/8 = 58mi/hr
t = d/s
= 638/58 = 11 hours
Select the correct answer from each drop-down menu.
The total area of the three triangles is
square units.
The area of the figure is
square units.
Answers
The total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
What is the triangle?The triangle can be defined as a three-sided polygon in geometry, and it consists of three vertices and three edges. The sum of all the angles inside the triangle is 180°.
From the figure, the area of triangles can be calculated using the:
Area = (1/2)height×base length
Area of three triangle = 1/2(4×6) + 1/2(6×4) + 1/2(4×6)
Area of three triangle = 1/2(24×3) = 36 square units
Area of the figure = area of three triangle + area of the rectangle
= 36 + 6×4
= 60 square units
Thus, the total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
Learn more about the triangle here:
brainly.com/question/25813512
#SPJ1

Use a geometric tool to draw a circle. Draw and measure a radius and a diameter of the circle .
Answers
Answer:
Attached is an example of a circle with a radius of 5 and a diameter of 10.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

the unit rate for each option. 9. Option A: $15.40 for 3.5 lbs of gummy bears
Answers
The unit rate for Option A is $4.4 per pound of gummy bears.
The unit rate for each option is a mathematical expression that compares two quantities of different measures by dividing one quantity by the other.
The unit rate is used to determine how much an item costs per unit of measure.
To find the unit rate for each option, we can use the following formula: Unit rate = price ÷ weight Option A: $15.40 for 3.5 lbs of gummy bears Unit rate = 15.40 ÷ 3.5Unit rate = $4.4 per pound of gummy bears.
Therefore, the unit rate for Option A is $4.4 per pound of gummy bears.
For more such questions on gummy bears
https://brainly.com/question/25831000
#SPJ8
Here is the complete question given below:
The unit rate for each option. 9. Option A: $15.40 for 3.5 lbs of gummy bears. $7.65 for 1.8 Ibs of gummy bears.
Find a slope of the line that passes through (7,9) and (1,14)
Answers
Answer:
-5/6
Step-by-step explanation:
Use rise over run (change in y divided by change in x):
slope = Δy / Δx = \(\frac{y_{2} - y_{1}}{x_{2} - x_{1}}\)
= (14 - 9) / (1 - 7) = 5 / -6 = -5/6
3x-1/4y=-2 solve for y
Answers
Answer:
y= 1/4(2+3x)
Step-by-step explanation:
The solution of the expression for the value of y is y = 8 + 12x.
What is an expression?Expression in maths is defined as the collection of numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
Numbers (constants), variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.
The given expression is 3x-1/4y=-2. The value of y will be calculated as below:-
3x-1/4y=-2
-(1/4)y = -2 - 3x
y = 4 ( 2 + 3x)
y = 8 + 12x
Therefore, the solution of the expression for the value of y is y = 8 + 12x.
To know more about an expression follow
https://brainly.com/question/723406
#SPJ2
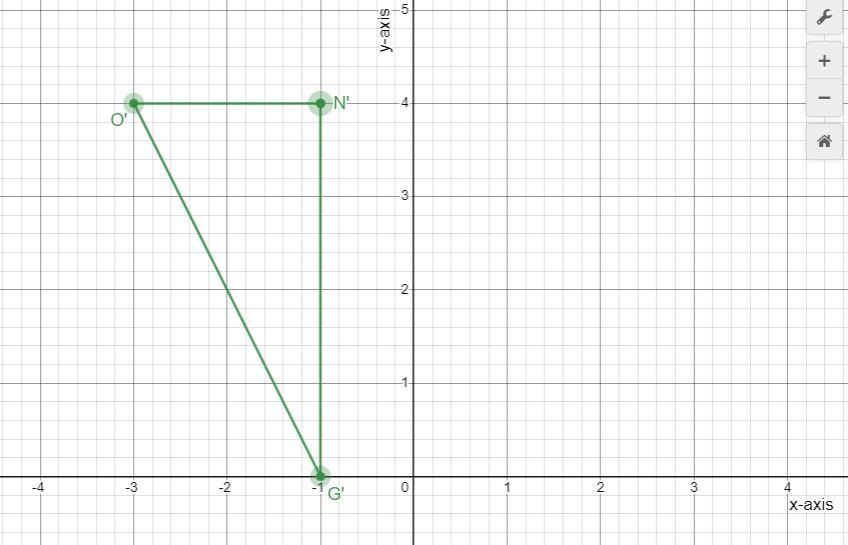
Rotation 90° clockwise about the origin
N
O
G

Answers
An image of triangle NOG after a rotation 90° clockwise about the origin is shown below.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation which moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
Next, we would apply a rotation of 90° clockwise about the origin to the coordinate of this triangle NOG in order to determine the coordinate of its image;
(x, y) → (y, -x)
Point N = (-4, -1) → Point N' (-1, 4)
Point O = (-4, -3) → Point O' (-3, 4)
Point G = (0, -1) → Point G' (-1, 0)
Read more on rotation here: brainly.com/question/28854313
#SPJ1
Could you explain to me the relationship of angles with three parallel lines cut by a transversal line? I have a project and need to understand how alternate exterior, alternate interior, etc angles relate in that picture…
Answers
We can draw the lines and relate the angles as:
Angles with one li

Say that a supplier claims they are 99% confident that their products will be in the interval of 50.02 to 50.38. You take samples and find that the 99% confidence interval of what they are sending is 50.01 to 50.39. What conclusion can be made
Answers
Answer:
The supplier becomes less accurate than they otherwise would have tried to claim. A further explanation is below.
Step-by-step explanation:
According to the provider, this same width of that same confidence interval would be as follows:
= \(50.38 - 50.02\)
= \(0.36\)
Depending on the input observed, the width including its confidence interval would be as follows:
= \(50.39 - 50.01\)
= \(0.38\)
As even the width of that interval again for survey asserted > the width including its confidence interval according to the provider's statement, we could conclude that such is the appropriate reaction.
What’s the answer pls I need help w my ixl hsjdhdhshshshddhdhdhdhdhdbdhzhzbxbxbx

Answers
Answer:
In explanation
Step-by-step explanation:
x= -1
3(-1)^2+7=0
= 10
x= 0
3(0)^2+7
y=7
x=1
3(1)^2+7
y=10
x=2
3(2)^2+7
=3(4)+7
=12+7
y=19
Solve using tangent and cosine

Answers
The value of side length x in diagram a) is 4.3mm and side length x in diagram b) is 309.7 m.
What are the sides of the triangle labelled x?The figures in the image are right triangles.
A)
angle D = 17 degree
Adjacent to angle D = 14 mm
Opposite to angle D = x
To solve for the missing side length x, we use the trigonometric ratio.
Note that: tangent = opposite / adjacent
Hence:
tan( 17 ) = x/14
x = tan( 17 ) × 14
x = 4.3mm
B)
angle Z = 82 degree
Adjacent to angle Z = 43.1 m
Hypotenuse = x
Using trigonometric ratio,
cosine = adjacent / hypotenuse
cos( 82 ) = 43.1 / x
x = 43.1 / cos( 82 )
x = 309.7 m
Therefore, the measure of x is 309.7 meters.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Suppose a certain outlet chain selling appliances has found that for one brand of
stereo system, the monthly demand is 240 when the price is $900. However, when
the price is $850, the monthly demand is 315. Assuming that the demand function
for this system is linear, write the equation for the demand function. Use p for
price and q for quantity. Find equilibrium point as well.
Answers
Using p for price and q for quantity, the demand function is; q = -3/2p + 1590
What is the demand function?Given that at;
The monthly demand at a price of $900 = 240
The monthly demand at a price of $850 = 315
We are told that the system is a linear function. Therefore demand function would be in the form of slope intercept form as;
q = mp + c
Where;
q = quantity demanded
p = price
m = slope
c = y-intercept
At a price of $900 with a monthly demand of 240 gives the equation;
240 = 900m + c ---(1)
At a price of $850 with a monthly demand of 315 gives the equation;
315 = 850m+ c ------(2)
Subtracting eqn 2 from 1 gives;
-75 = 50m
m = -75/50
m = -3/2
Substituting m = -3/2 into equation 1;
240= -3/2(900) + c
c = 240 + 3/2(900)
c = 1590
Therefore the demand function can be given as; substituting m and c into equation 5, we have; q = -3/2p + 1590
Read more about Demand Function at; https://brainly.com/question/14375213
#SPJ1
Please answer this correctly

Answers
Answer:
5 cm
Step-by-step explanation:
Use lenght times wight times height
So, you need to do 4 times 4 times ________ is 80
The function ƒ(x) = x−−√3 is translated 3 units in the negative y-direction and 8 units in the negative x- direction. Select the correct equation for the resulting function.

Answers
Answer:
\(f(x)=\sqrt[3]{x}\) \(3~units\: down\)
\(f(x)=\sqrt[3]{x} -3\) \(8 \: units \: left\)
\(f(x+8)=\sqrt[3]{(x+8)} -3\)
----------------------------
Hope it helps..
Have a great day!!
Answer:
its not B that what i put and i missed it
Step-by-step explanation: