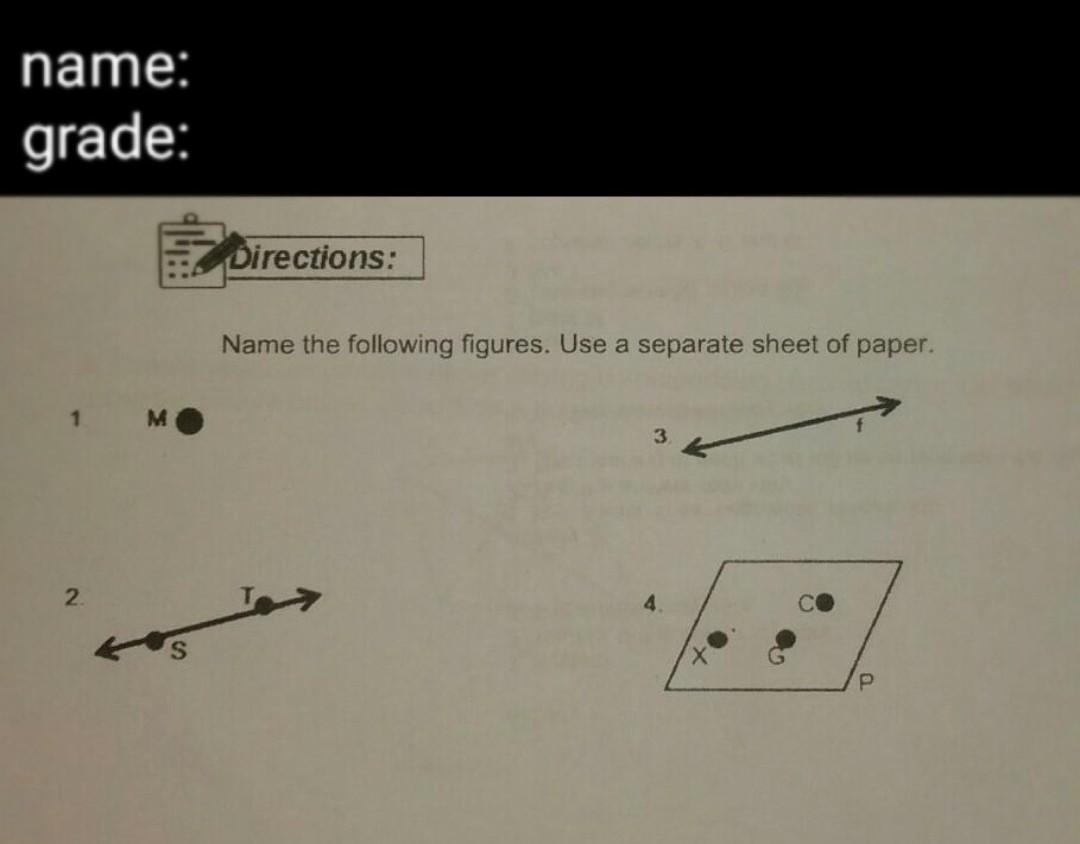
Answers
I can only answer 1, 2, and 4 :')
1. point
2. line
3. ?
4. plane
Related Questions
Find an equation of a plane through the point (-5, -5, -2) which is parallel to the plane 4x - 5y + 3z -6 in which the coefficient of x is 4.
Answers
An equation of the plane through the point (-5, -5, -2) that is parallel to the plane 4x - 5y + 3z - 6 = 0 and has a coefficient of x as 4 is 4x - 5y + 3z + 1 = 0.
To find an equation of a plane through the point (-5, -5, -2) that is parallel to the plane 4x - 5y + 3z - 6 = 0 and has a coefficient of x as 4, we can use the concept that parallel planes have the same normal vectors.
The given plane has a normal vector (4, -5, 3) since the coefficients of x, y, and z represent the components of the normal vector. To find an equation of a parallel plane, we can use the same normal vector.
Using the point-normal form of the equation of a plane, the equation can be written as:
4(x - x₁) - 5(y - y₁) + 3(z - z₁) = 0
Substituting the coordinates of the given point (-5, -5, -2) as (x₁, y₁, z₁):
4(x + 5) - 5(y + 5) + 3(z + 2) = 0
Expanding and simplifying the equation:
4x + 20 - 5y - 25 + 3z + 6 = 0
4x - 5y + 3z + 1 = 0
Therefore, an equation of the plane through the point (-5, -5, -2) that is parallel to the plane 4x - 5y + 3z - 6 = 0 and has a coefficient of x as 4 is 4x - 5y + 3z + 1 = 0.
Learn more about coefficient here:-
https://brainly.com/question/30524977
#SPJ11
PLEASE HEP ME WITH THIS ONE

Answers
Answer:
Your answer is about 50.27 or 50.26548
Step-by-step explanation:
A = pi*r²
A = pi*4²
A = 50.26548
50 POINTS MARKING BRAINLEIST PLS ANSWER ASAP

Answers
ANSWER IN THE ATTACHMENT ABOVE......

Find fog, gof, and gº g. f(x) = -3x, g(x) = x + 7 (a) fog (b) gof (c) gᵒg
Answers
The functions f(x) = -3x and g(x) = x + 7 into the composition is a. fog(x) = -3x - 21. b. gof(x) = -3x + 7. c. gºg(x) = x + 14.
To find fog, gof, and gºg, we need to substitute the functions f(x) = -3x and g(x) = x + 7 into the composition formulas.
(a) fog:
fog(x) = f(g(x))
fog(x) = f(x + 7)
fog(x) = -3(x + 7)
fog(x) = -3x - 21
Therefore, fog(x) = -3x - 21.
(b) gof:
gof(x) = g(f(x))
gof(x) = g(-3x)
gof(x) = -3x + 7
Therefore, gof(x) = -3x + 7.
(c) gºg:
gºg(x) = g(g(x))
gºg(x) = g(x + 7)
gºg(x) = (x + 7) + 7
gºg(x) = x + 14
Therefore, gºg(x) = x + 14.
Learn more about functions here
https://brainly.com/question/25638609
#SPJ11
find the area of the polygon

Answers
Answer:
Area=78m^2
Step-by-step explanation:
4*12=48m^2 <-- The area of a rectangle LxW
12*5=60 60/2=30 <-- The area of a triangle (HxB)/2
30+48=78m^2 Add them together to get the total area
In triangle ABC, ZA-25°, ZC-55° and AB-60. What are the approximate measures of the remaining side lengths of
the triangle?
Answers
We can use the Law of Sines and some trigonometric functions to approximate the remaining side lengths of the triangle ABC. We find that the length of side BC is approximately 48.4 and the length of side AC is approximately 54.1.
Let's start by using the Law of Sines, which states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides of the triangle. We can use this law to find the ratio of the lengths of the sides of triangle ABC.
sin(A)/a = sin(B)/b = sin(C)/c
Since we know the measure of angle B and the length of side AB, we can use this ratio to find the length of side BC:
sin(60°)/AB = sin(55°)/BC
Solving for BC, we get:
BC ≈ AB * sin(55°) / sin(60°) ≈ 48.4
Next, we can use the Law of Cosines to find the length of side AC. This law relates the lengths of the sides of a triangle to the cosine of one of its angles:
c^2 = a^2 + b^2 - 2ab*cos(C)
We know the length of side AB and can use the Law of Sines to find the sine of angle A:
sin(A)/AB = sin(60°)/BC
sin(A) ≈ AB * sin(60°) / BC ≈ 0.866
Now we can use the fact that the sum of the angles in a triangle is 180° to find the measure of angle C:
C = 180° - A - B ≈ 100°
Substituting the given values into the Law of Cosines, we can solve for the length of side AC:
AC^2 = AB^2 + BC^2 - 2ABBCcos(C)
AC ≈ sqrt(AB^2 + BC^2 - 2ABBCcos(C)) ≈ 54.1
Therefore, the approximate measures of the remaining side lengths of triangle ABC are BC ≈ 48.4 and AC ≈ 54.1.
Learn more about Triangle:
brainly.com/question/2773823
#SPJ11
A crane has a cable with a breaking strain of 6400kg measured to 2 significant figures it is used to lift crates which weigh 90kg measured to the nearest 10kg what is the greatest number of crates that can safely be lifted at one time without breaking the cable some working must be shown
Answers
Answer:
100/2=50
lower bound of 6400kg = 6350kg
10/2=5
upper bound of 90kg = 95kg
6350kg/95kg=66kg
Step-by-step explanation:
this is right
Please help me for brainliest!! There is a picture! Answer choices : 2, 4, 6, 8

Answers
Answer:
x = 2
Step-by-step explanation:
The 2 triangles are similar, thus the ratios of corresponding sides are equal, that is
\(\frac{x}{8}\) = \(\frac{3.5}{14}\) ( cross- multiply )
14x = 28 ( divide both sides by 14 )
x = 2
Solve for d.
26 = 100d
d= 26
d= 0.26
d= 2.6
d= 0.026
Answers
Have a lovely day :)
how have the lines been transformed? Line B is ___, ___, and shifted ___.

Answers
A line is said to be flat when it has a small slope, while a line is said to be steep when it has a large slope.
Let's find the slope of both lines.
Apply the slope formula:
\(m=\frac{y2-y1}{x2-x1}\)• Slope of line A
Take the points:
(x1, y1) ==> (-1, 1)
(x2, y2) ==> (-2, 4)
\(m=\frac{4-1}{-2-(-1)}=\frac{4-1}{-2+1}=\frac{3}{-1}=-3\)• Slope of line B
Take the points:
(x1, y1) ==> (4, -1)
(x2, y2) ==> (0, -1)
\(m=\frac{-1-(-1)}{4-0}=\frac{-1+1}{4-0}=\frac{0}{4}=0\)The slope of line A is -3( negative slope)
The slope of line B is 0
The greater the slope, the steeper the line.
• Since line B has a greater slope than line A, we can say it is steeper.
,• Also since Line B is a horizontal line, it is flatter than line A
,• The slope of a horizontal line is greater than the slope of a line with a neagtive slope, we can say that line B shifted upward
Thus, we can say:
Line B is flatter, horizontal and shifted upward
ANSWER:
Line B is flatter, horizontal, and shifted upward
hey can someone help this is due today

Answers
Answer:
Step-by-step explanation:
rectangle
parallelogram
Quadrilateral
A population proportion is to be estimated. Estimate the minimum sample size needed to achieve the specified margin of error with a 95% degree of confidence. E=0.012. Please show step by step and explain where you pull actual numbers from.
Answers
The minimum sample size required is 666.
Let's discuss it further below.
To estimate the minimum sample size needed to achieve a specified margin of error (E) with a 95% degree of confidence, we can use the following formula:
n = (Z^2 * p * (1-p)) / E²
Here, n is the sample size, Z is the Z-score for the desired confidence level, p is the population proportion, and E is the margin of error.
Step 1: Determine the Z-score
For a 95% degree of confidence, the Z-score is 1.96. This value comes from a standard normal distribution table, which provides the Z-scores for different confidence levels.
Step 2: Determine the population proportion (p)
Since we don't have information about the population proportion, we'll assume the worst-case scenario, which is when p = 0.5 (50%). This will give us the maximum variance and result in the largest required sample size.
Step 3: Plug the values into the formula
n = (1.96^2 * 0.5 * (1-0.5)) / 0.012²
Step 4: Calculate the sample size
n = (3.8416 * 0.5 * 0.5) / 0.000144
n ≈ 665.28
Since we cannot have a fraction of a sample, we need to round up to the nearest whole number. So, the minimum sample size required is 666.
Learn more about standard normal distribution.
brainly.com/question/29509087
#SPJ11
Find the discriminant value of 25q^2-40q+16=0
Please show work!!!
Answers
The discriminant value of a quadratic equation is b^2 - 4ac.
We can see here, in this quadratic equation, 25 is a, 40 is b and 16 is c (as in ax^2 + bx + c)
Applying it to the discriminant value = 40^2 - 4 x 25 x 16 = 1600 - 1600 = 0.
(And since the discriminant value is 0, the quadratic function has 1 repeated real root.)
Evaluate, given f(x) = 6x – 9.
a) f(4)
B) f(1/2)
Answers
B)f(1/2)=6(1/2)-9=3-9= -6
please help ill mark brilliant

Answers
Answer:
i think its 12
Step-by-step explanation:
what is 30 grams in ounces?
Answers
Answer:
1.05821886 ounces
Step-by-step explanation:
To convert 30 grams to ounces, use the conversion factor 1 ounce = 28.3495 grams.
how many times does 50 go into 264
Answers
Answer:
5 times. Remaining is 7/25.
Step-by-step explanation:
"How many times does 50 into 264" represents 264/50.
Let's divide 264 by 50:
264 / 50 = 5 with the remaining of 14.
Let's turn 14 into a simplified fraction:
14/50
=7/25.
Your simplified answer is:
50 goes into 264 5 and 7/25 times.
Write the equation of the line in slope-intercept form that passes through (3, 5) and is perpendicular to the line
3y + 4x = 12
Answers
Answer:
Step-by-step explanation:
find the gradient of given equation:
3y+4x=12
3y= -4x+12
y= -4/3x+4
gradient= -4/3
perpendicular gradient:
m1xm2=-1
-4/3m2=-1
-4m2=-3
m2= 3/4
find y-intercept by inputting coordinates in y=mx+c
5=3/4(3)+c
5=9/4+c
5-9/4=c
c= - 11/4
equation:
y=3/4x-11/4
Can someone please help me?

Answers
3] Question 5 Consider the vector field F(x, y, z) = y cos (xy) i + x cos (xy)j – sin zk. (i) Calculate the curl of the vector field F. State whether F is conservative. (ii) Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve r(t) = n* i + t}j + tcos atk, 15t52. Calculate the scalar line integral of the vector field. F. dr. F.dr.
Answers
Given vector field, F(x, y, z) = y cos (xy) i + x cos (xy) j – sin z k To calculate the curl of F, we need to take the curl of each component and subtract as follows,∇ × F = ( ∂Q/∂y - ∂P/∂z ) i + ( ∂P/∂z - ∂R/∂x ) j + ( ∂R/∂x - ∂Q/∂y ) k...where P = y cos(xy), Q = x cos(xy), R = -sin(z)
Now we calculate the partial derivatives as follows,
∂P/∂z = 0, ∂Q/∂y = cos(xy) - xy sin(xy), ∂R/∂x = 0...
and,
∂P/∂y = cos(xy) - xy sin(xy), ∂Q/∂z = 0, ∂R/∂y = 0
Therefore,
∇ × F = (cos(xy) - xy sin(xy)) i - sin(z)j
The curl of F is given by:
(cos(xy) - xy sin(xy)) i - sin(z)j.
To state whether F is conservative, we need to determine if it is a conservative field or not. This means that the curl of F should be zero for it to be conservative. The curl of F is not equal to zero. Hence, the vector field F is not conservative. Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve:
r(t) = n* i + t}j + tcos atk, 15t52.
The curve C is defined as follows,r(t) = ni + tj + tk cos(at), 0 ≤ t ≤ 1Given vector field, F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk Using the curve parameterization, we get the line integral as follows,∫CF.dr = ∫10 F(r(t)).r'(t)dt...where r'(t) is the derivative of r(t) with respect to t
= ∫10 [(t cos(at))(cos(n t)) i + (n cos(nt))(cos(nt)) j + (-sin(tk cos(at)))(a sin(at)) k] . [i + j + a tk sin(at)] dt
= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) + (-a t sin(at) cos(tk))(a sin(at))] dt
= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) - a^2 (t/2) (sin(2at))] dt
= [sin(at) sin(nt) - (a/2) t^2 cos(2at)]0^1
= sin(a) sin(n) - (a/2) cos(2a)
The vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is given. Firstly, we need to calculate the curl of F. This involves taking the curl of each component of F and subtracting. After calculating the partial derivatives of each component, we get the curl of F as (cos(xy) - xy sin(xy)) i - sin(z)j. Next, we need to determine whether F is conservative. A conservative field has a curl equal to zero. As the curl of F is not equal to zero, it is not a conservative field. In the second part of the problem, we have to calculate the scalar line integral of the vector field F. dr along the curve C joining the origin to the point with coordinates (1, 2V2, 2). We use the curve parameterization to calculate the line integral. After simplifying the expression, we get the answer as sin(a) sin(n) - (a/2) cos(2a).
The curl of the given vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is (cos(xy) - xy sin(xy)) i - sin(z)j. F is not conservative as its curl is not zero. The scalar line integral of the vector field F along the curve C joining the origin to the point with coordinates (1, 2V2,2) is sin(a) sin(n) - (a/2) cos(2a).
To learn more about curve parameterization visit:
brainly.com/question/12982907
#SPJ11
HELP!!!
A car manufacturer collects data on the number of gallons of gasoline left in the gas tank after driving for different numbers of miles. The manufacturer creates a scatter plot of the data and determines that the correlation coefficient is −0.92.
Select each true statement based on this correlation coefficient.
A.) There is a weak correlation between the number of miles driven and the gallons of gasoline left in the tank.
B.) There is a negative correlation between the number of miles driven and the gallons of gasoline left in the tank.
C.) There is no correlation between the number of miles driven and the gallons of gasoline left in the tank.
D.) There is a linear correlation between the number of miles driven and the gallons of gasoline left in the tank.
E.) There is a strong correlation between the number of miles driven and the gallons of gasoline left in the tank.
Answers
The statement that is true about the variables analyzed is that there is a negative correlation between the number of miles driven and the gallons of gasoline left in the tank.
What is correlation?This refers to the relation or connection between two or more variables. In this case:
Amount of gasolineNumber of milesWhat does -0.92 mean?This has the sign -, which shows the correlation is negative. This implies that as the number of miles increase the amount of gasoline decreases.
Learn more about gasoline in: https://brainly.com/question/12847098
#SPJ1
at a student government fundraiser, a notebook costs $6 and a t-shirt costs $12. if the total received for 90 items was $600, how many notebooks were sold?
Answers
As per the given costs, 80 notebooks were sold at the student government fundraiser.
Let the number of notebooks sold be = N
Let the number of t-shirts sold be = T
Setting the equation, representing the total number of items sold
N + T = 90
or N = 90 - T.
Setting the equation, representing the total amount -
6N + 12T = 600
Substituting this value of N into the second equation -
6(90 - T) + 12T = 600
540 - 6T + 12T = 600
6T = 600 - 540
6T = 60
T = 60 / 6
T = 10
Substituting the value of T back into the first equation to find the value of n or total notebooks -
N + 10 = 90
N = 90 - 10
N = 80
Read more about costs on:
https://brainly.com/question/19104371
#SPJ4
Calculate the variance and standard deviation for samples with the
following statistics.
Calculate the variance and standard deviation for samples with the following statistics. a, n = 11, Σx = 88, Σx=22 b. n=42, Σx = 385, Σx=90 c. n = 20, Σx = 15, Σχ=14 a. The variance is The stan
Answers
The variance for the sample is not valid. The variance is -352.98 and the standard deviation is 18.77 for sample (b), while for sample (c), the variance is -10.263 and the standard deviation is 3.20.
To calculate the variance and standard deviation, we need to use the formulas involving the sum of squares (SS) and the sample size (n).
(a) We have: n = 11, Σx = 88, Σx² = 22
The variance (σ²) is calculated as:
σ² = (Σx² - (Σx)²/n) / (n - 1)
Substituting the values into the formula:
σ² = (22 - (88)²/11) / (11 - 1)
= (22 - 7744/11) / 10
= (-7700/11) / 10
= -700/11
= -63.636
Since variance cannot be negative, the variance for this sample is not valid.
The standard deviation (σ) is the square root of the variance:
σ = √(-700/11)
= √(-63.636)
= √(63.636)i
= 7.982i
(b) We have: n = 42, Σx = 385, Σx² = 90
Using the same formulas:
σ² = (Σx² - (Σx)²/n) / (n - 1)
= (90 - (385)²/42) / (42 - 1)
= (90 - 14822/42) / 41
= (-14552/42) / 41
= -352.98
The variance is -352.98.
σ = √(-352.98)
= √(352.98)i
= 18.77i
(c) We have: n = 20, Σx = 15, Σx² = 14
Using the same formulas:
σ² = (Σx² - (Σx)²/n) / (n - 1)
= (14 - (15)²/20) / (20 - 1)
= (14 - 225/20) / 19
= (-195/20) / 19
= -10.263
The variance is -10.263.
σ = √(-10.263)
= √(10.263)i
= 3.20i
In summary:
(a) The variance is not valid as it is negative.
(b) The variance is -352.98 and the standard deviation is 18.77.
(c) The variance is -10.263 and the standard deviation is 3.20.
To know more about variance refer here:
https://brainly.com/question/10687815#
#SPJ11
PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!!PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!!

Answers
Answer:
268.083
Step-by-step explanation:
volume of a sphere = 4/3 times pi times r^3. 4/3(pi)(4^3) = 268.083
what is the total force on the bottom of a swimming pool 28.5 m by 7.5 m whose uniform depth is 1.6 m ?
Answers
The total force on the bottom of the swimming pool is 3.35 × 10⁶ N.
The total force on the bottom of a swimming pool can be calculated by using the formula: F = pA, where F is the force, p is the pressure, and A is the area of the bottom of the pool.
First, we need to calculate the area of the bottom of the pool:
A = 28.5 m × 7.5 m = 213.75 m²
Next, we need to calculate the pressure on the bottom of the pool. The pressure is equal to the weight of the water above the bottom of the pool, which can be calculated by multiplying the density of water (ρ), the acceleration due to gravity (g), and the height of the water (h):
p = ρgh = (1000 kg/m³)(9.8 m/s²)(1.6 m) = 15680 N/m²
Finally, we can calculate the total force on the bottom of the pool by multiplying the pressure and the area:
F = pA = (15680 N/m²)(213.75 m²) = 3.35 × 10⁶ N
For more similar questions on force :
brainly.com/question/25239010
#SPJ11
Find the value of x. Round your answer to the nearest tenth.
7
sin 330
IX
Answers
Step-by-step explanation:
first u should write value of sin 330
sin 330 =-12
the nearest tenth 7 ×-12
what is the answer please i need help -2.6f+0.4f-14-4
Answers
Answer: \(-2.2f-18\)
Step-by-step explanation:
\(-2.6f+0.4f-14-4=f(-2.6+0.4)+(-14-4)=-2.2f-18\)
Find the volume of the pyramid, Write your answer as a fraction or mixed number.

Answers
4 divided by 3= 1 1/3
Length(l) of rectangular pyramid = 2ft.
Width(w) of the rectangular pyramid = 1ft.
Hight(h) of the rectangular pyramid = 2ft.
Formula Used:-Volume of Rectangular Pyramid = \(\sf{\frac{1}{3}×Length×Width×Hight}\)
Solution:-➾\(\sf{\frac{1}{3}×l×w×h}\)(putting the value of l, w and h from above.)
➾\(\sf{\frac{1}{3}×2×1×2}\)
➾\(\sf{\frac{1}{3}×4}\)
➾\(\sf{\frac{4}{3}}\)
Therefore, volume of the given rectangular pyramid = \(\sf{\frac{4}{3} ft^3}\).
And it can be rewritten in the form of mixed fraction as \(\sf{\frac1{1}{3} ft^3}\).
Line t passes through (4, 5) and is perpendicular to the line shown on the coordinate grid. a coordinate plane with a line passing through two points at 0 comma 3 and 7 comma 2 What is the equation of line t in standard form?
Answers
The equation of line t in standard form is: B. 7x - y = 23.
How to determine an equation of this line?In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):
y - y₁ = m(x - x₁)
Where:
x and y represent the data points.m represent the slope.First of all, we would determine the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (2 - 3)/(7 - 0)
Slope (m) = -1/7
Since the equation of this line is perpendicular to the line t, the slope is given by;
m₁ × m₂ = -1
-1/7 × m₂ = -1
m₂ = -7/-1
Slope, m₂ = 7
At data point (4, 5) and a slope of 7, a linear equation for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - 5 = 7(x - 4)
y = 7x - 23
7x - y = 23
Read more on point-slope here: brainly.com/question/24907633
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Answer:
7x - y = 23
Step-by-step explanation: 7x - y = 23**
If P(B)=
4
1
,P(A∪B)=
2
1
and P(A∣B)=
3
2
, then which of the following statements is true? A) P(A)=
3
1
B) P(A∩B)=
12
1
C) P(B∣A)=
5
1
D) A and B are not independent.
Answers
None of the statements A, B, or C can be determined to be true based on the given information. we do not have enough information to determine the values of P(A), P(A∩B), or P(B|A) from the given probabilities.
To determine which statement is true, let's analyze the given information. We have:
P(B) = 4/1
P(A∪B) = 2/1
P(A|B) = 3/2
Let's evaluate each statement:
A) P(A) = 3/1
This statement is not directly supported by the given information. We cannot determine the value of P(A) solely based on the provided probabilities.
B) P(A∩B) = 12/1
This statement is also not supported by the given information. We do not have enough information to determine the value of P(A∩B).
C) P(B|A) = 5/1
This statement is not supported by the given information. We do not have any direct information about P(B|A), so we cannot determine its value.
D) A and B are not independent.
To determine whether A and B are independent, we can check if P(A∩B) = P(A) * P(B). However, as mentioned earlier, we do not have enough information to determine the value of P(A∩B). Therefore, we cannot conclude whether A and B are independent based on the given information.
In summary, none of the statements A, B, or C can be determined to be true based on the given information. The only conclusion we can draw is that we do not have enough information to determine the values of P(A), P(A∩B), or P(B|A) from the given probabilities.
Learn more about probabilities.
https://brainly.com/question/29381779
#SPJ11