hola , alguien me podria decir cuanto es x+y=47 , tomando en cuenta que 40 alumnos y 14 profesores van de viaje , y en el hotel que se quedaran , los alumnos dormiran en cuartos dobles (2 camas) y los profesores en sencillas (1 cama) , y sumando en total son 47 habitaciones y 79 camas , y la incognita x es las habitaciones sencillas y la incognita y son las habitaciones dobles
Answers
Answer:
Step-by-step explanation:
40s=40×2=x
14t=14×1=y
40s=80
x=80
14t=14
y=14
Related Questions
A point P(3, k) is first transformed by E¹[0, 2] and then by E²[0,3/2] so that the final image is (9, 12), find the value of k.
![A point P(3, k) is first transformed by E[0, 2] and then by E[0,3/2] so that the final image is (9, 12),](https://i5t5.c14.e2-1.dev/c-qa-images/contents/attachments/1eOlyY8yY58OVpLHEWTFwopNqYjHDzo4.jpeg)
Answers
Hello,
The first transform E1 is the homothetie of center (0,0) and ratio=2
The second transform E2 is the homothetie of center (0,0) and ratio=3/2
P=(3,k)
P'=E1(P)= E1((3,k))=(2*3,2*k)=(6,2k)
P''=E2(P')=E2(6,2k)=(3/2*6,3/2*2*k)=(9,3k)=(9,12)
==> 3k=12
k=4
Solve the Following expression d=5 2d+4d-9-7=
Answers
Answer:
14
Step-by-step explanation:
d=5 so
2(5)+4(5)-9-7
10+20-9-7
30-9-7
21-7
14
Answer:
2×5+4×5-9-7.
10+20-9-7.
=14.
Answer:
2×5+4×5-9-7.
10+20-9-7.
=14.
what is the dilation of this the bigger one is the original size.

Answers
Point P(6,6)
Point P'(2, 2)
To determine the dilation:
\(\begin{gathered} 6x=2 \\ x=\frac{2}{6} \\ x=\frac{1}{3} \end{gathered}\)The dilation of this image is 1/3.
im lost!! can someone please help me. will vote brainliest

Answers
Answer:
Answer is >= 1. The reason is that you can't take the square root of a number and it be a rational number. So you have to avoid having a number that is negative under the square root symbol. In addition, you have to make sure you don't have a zero in the denominator because that would make the answer undefined.
Answer is C
Step-by-step explanation:
Answer:
I belive the answer is c
Try using desmos cauculater ;)
The box plots show the weights, in pounds, of the dogs in two different animal shelters.One-half of the dogs in each shelter are between which weights?
Answers
One-half of the dogs in each shelter are between the weights represented by the first and third quartiles, which are approximately 20-55 pounds for the first shelter and 25-65 pounds for the second shelter, respectively.
A box plot is a visual representation of a set of data that shows the median, quartiles, and outliers of the data. The box represents the middle 50% of the data, with the bottom and top edges of the box representing the first and third quartiles, respectively. The line inside the box represents the median, or the middle value of the data set. The "whiskers" extend from the edges of the box to the minimum and maximum values of the data set, but outliers beyond the whiskers are represented as individual points.
Now, let's look at the two box plots showing the weights of dogs in two different animal shelters. One-half of the dogs in each shelter are between the first and third quartiles, which are represented by the edges of the box in each plot.
If we take the first box plot, we can see that the first quartile is approximately 20 pounds and the third quartile is approximately 55 pounds. Therefore, one-half of the dogs in this shelter weigh between 20 and 55 pounds.
To know more about shelter visit:-
https://brainly.com/question/14394978
#SPJ11
Help please thanks!!!
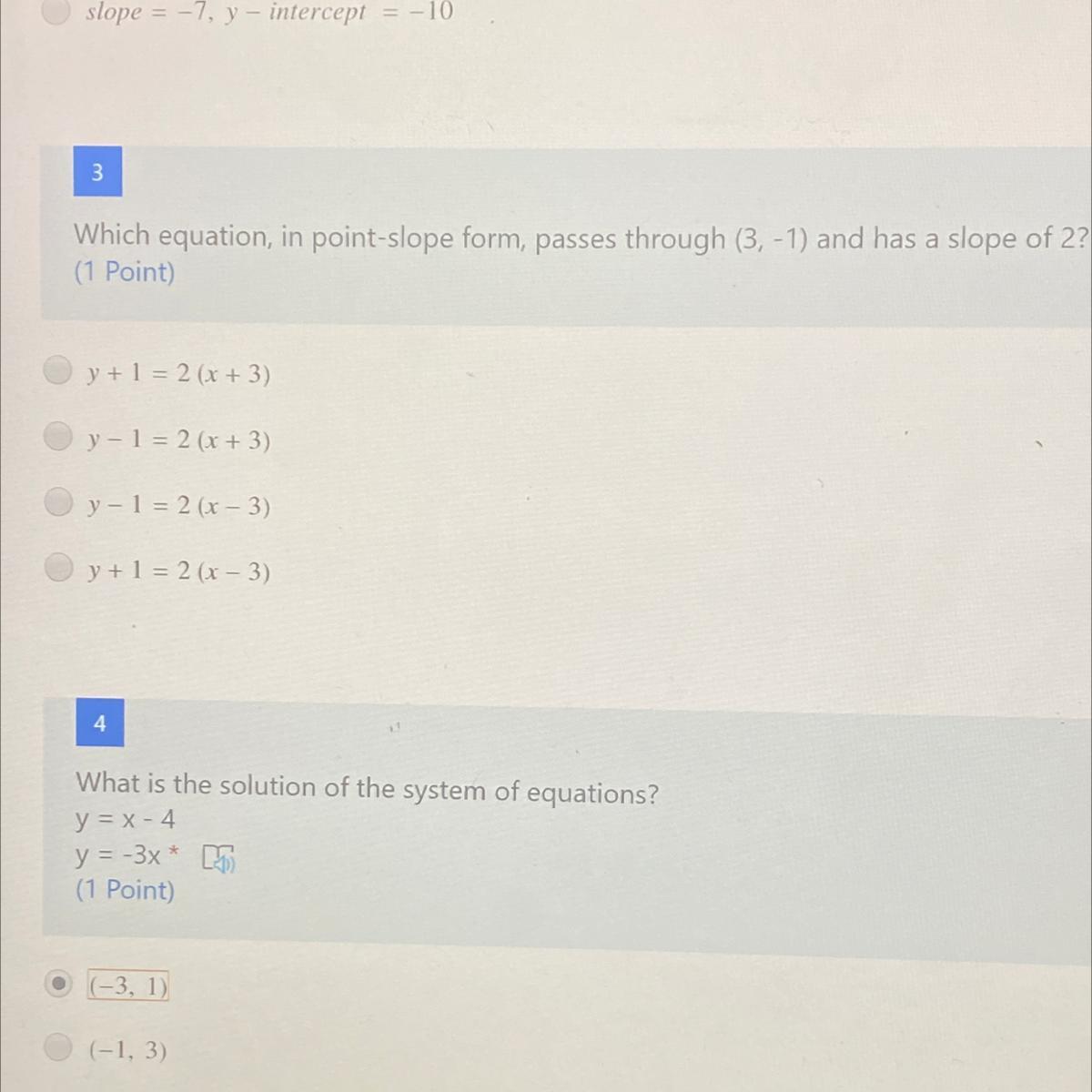
Answers
Answer:
The 4th choice which is y+1=2(x-3)
The three principles that result in high reliability include having a _____ sample, less-variable observations, and many cases.
Answers
High reliability is a term used in scientific research that describes measures that are consistent, valid, and trustworthy. Reliable measures are crucial in any discipline where research is conducted, including psychology. It is important to have reliable measures because researchers want their results to be consistent and replicable.
There are three principles that result in high reliability: large sample sizes, less-variable observations, and numerous cases. A large sample size is necessary to ensure research results are consistent and more representative of the population. In addition, less-variable observations are needed to avoid extraneous variables that could influence observations and lead to inconsistencies over time. Researchers can create controlled settings to eliminate extraneous variables, and by doing so, develop more reliable measures.
Finally, researchers must test the same theory or hypothesis on many cases. By doing so, researchers can observe whether their hypothesis is valid across a large number of cases. This is important because observing many cases allows researchers to generalize their findings to the population. These three principles combined contribute to the development of more reliable measures, resulting in high reliability.
Know more about High reliability here:
https://brainly.com/question/32509658
#SPJ11
Which is the correct representation of 6/1?

Answers
The correct representation of 6/1 is in figure A.
Given:
The four figures with shaded regions and unshaded regions.
To find:
The figure with the correct representation of 6/1.
Solution:
In figure A
Fraction of one box =\(\frac{1}{1}\)
There are six individual boxes that will be represented as:
\(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}=\frac{6}{1}\)
In figure B
The number of shaded regions = 5
The total number of regions = 6
The representation will be :
\(\frac{\text{Shaded region}}{\text{Total regions}}=\frac{5}{6}\)
In figure C
Fraction of one box =\(\frac{1}{1}\)
There are five individual boxes that will be represented as:
\(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}=\frac{5}{1}\)
In figure D
The number of shaded regions = 1
The total number of regions = 1
The representation will be:
\(\frac{\text{Shaded region}}{\text{Total regions}}=\frac{1}{6}\)
The correct representation of 6/1 is in figure A.
Learn more about fraction here:
brainly.com/question/1301841?referrer=searchResults
brainly.com/question/1301963?referrer=searchResults
The sociology of sport journal examined the sat scores of male student athletes at ncaa division 1 institutions. the sat score is used to determine whether athletes are eligible to participate in athletics during their first year, with the ncaa requiring a minimum score of 700. suppose that sat scores of athletes on scholarship have an average of 950 and a standard deviation of 200. assuming the distribution of sat scores is approximately normal, what percentage of athletes will not be eligible their first year?
Answers
Using the properties of standard deviation , 10.56% of people will not be eligible in the first year.
A standard normal table is a mathematical representation of the values of the components of the normal distribution's cumulative distribution functions.
It is also referred to as the Z table or the unit normal table .The likelihood that a statistic will be observed below, above, between, or on the normal distribution, which comprises all normal distributions, is determined using this formula. It is common practice to transform a normal to a standard normal before using the standard normal table to calculate probabilities since there are an unlimited number of possible normal distributions, making it impossible to write probability tables for each one.Given mean = 950
SD = 200
data value = 700
Z score = (700-950) ÷ 200 = -1.25
Therefore the p-value corresponding to the z-score is : 0.1056
therefore the required percentage = 10.56%
Hence 10.56% of people will not be eligible in the first year.
To learn more about standard deviation visit:
https://brainly.com/question/12402189
#SPJ4
pls help asap if you can!!

Answers
The ∆ABC is an isosceles triangle and have the base angles m∠A and m∠C equal to 51° and the angle m∠B is equal to 78°.
What is an Isosceles triangleAn isosceles triangle have the measure of its base angles to be equal, and the sum of the interior angles sum up to 180°.
Given that sides AB ≅ BC, then the triangle ∆ABC has two sides with similar length and base angles so;
angles m∠A and m∠C are the base angles are both equal to 51°
m∠B = 180° - (51 + 51)° {sum of interior angles of a triangle}
m∠B = 180° - 102°
m∠B = 78°
Therefore, the isosceles triangle ∆ABC have the base angles m∠A and m∠C equal to 51° and the angle m∠B is equal to 78°.
Read more about Isosceles triangle here:https://brainly.com/question/1475130
#SPJ1
3x^2y^2/6xy
please answer asap
Answers
Answer:
-3xy • (xy - 2)
Step-by-step explanation:
if ur supposed to be simplyfying it that should be the answer i think
Answer: 3xy⋅(xy−2) Your Welcome:)
:
passes through (-6,2) and is parallel to the line whose equation is 2x-3y=12
Answers
\(Answer:\large\boxed{y=\frac{2}{3} x+6}\)
Step-by-step explanation:
First let's convert 2x - 3y = 12 into \(y = mx + b\) form.
In order to do this, solve for y.
\(2x-3y=12\)
\(-3y=-2x+12\)
\(y=\frac{2}{3} x-4\)
This shows us that the slope is \(\boxed{\frac{2}{3}}\)
Now we use the point-slope formula:
\((y-y1)=m(x-x1)\)
where m is the slope and y1 and x1 are the point the line passes through
Using the point (-6,2) and slope, 2/3, we can find the equation:
\((y-2)=\frac{2}{3} (x-(-6))\)
\((y-2)=\frac{2}{3} (x+6)\)
\((y-2)=\frac{2}{3} x+4\)
\(\large\boxed{y=\frac{2}{3} x+6}\)
Use the equation F= (HG/S)+ G-A in my case is F=(1000/2)+0-15 please solve
F=father
HG=Hours on Genshin Impact
S=Showers
G= girls
A = age
Answers
The given equation and values, the value of F, which represents "father" in this context, is 485.
Using the equation F=(HG/S)+G-A, and substituting the given values, we get:
F = (1000/2) + 0 - 15
F = 500 + 0 - 15
F = 485
Therefore, based on the given equation and values, the value of F, which represents "father" in this context, is 485.
It's important to note that this equation is not a scientifically valid or meaningful equation, and is not intended for serious use in any context.
for such more question on equation
https://brainly.com/question/17482667
#SPJ11
Calculate the distance between two points (-8,9) and (4,4)
Answers
If A=(-8,9) and B=(4,4), using the formula for distance between two points, we get:
\(\begin{gathered} d(A,B)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \Rightarrow d(A,B)=\sqrt[]{(4-(-8))^2+(4-9)^2}=\sqrt[]{(12)^2+(-5)^2} \\ \Rightarrow d(A,B)=\sqrt[]{144+25}=\sqrt[]{169}=13 \\ d(A,B)=13 \end{gathered}\)Therefore, the distance between A and B is 13 units
Formula for distance between two points:
\(d(A,B)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}\)Various types of doctors attended a large medical conference. Someone leading a session asked the 30
doctors in attendance how many years of experience they each had. The 15 dermatologists at the session
had an average of 8 years of experience.
For which population is 8 years a legitimate estimate of the average experience?
Choose 1 answer:
The dermatologists at that session only
B
All doctors at that session only
С
All dermatologists at that conference only
All doctors at that conference only
Answers
Answer: The dermatologists at that session only
Step-by-step explanation:
It was on a Khan Academy practice.
A charity is holding a benefit at an Italian restaurant. The owner of the restaurant offers to donate $200 in addition to $4 for each person that
attends. Write an equation where d is the total donation and p in the number of people that attend.
Answers
Answer:
200 divided 4
Step-by-step explanation:
A box of mass 20 kg is being pushed up a slope of 15 m long with a
constant speed of 30 m/s as shown in the figure below. What is the
gravitational potential energy? (g= 9.8m/s²)
Answers
The gravitational potential energy is 2940 Joules
What is potential energy?The formula for gravitational potential energy is expressed as;
Gravitational Potential energy = m g h
Where;
m is the massg is the acceleration due to gravityh is the height of the objectSubstitute the values into the formula;
⇒ 20 × 9. 8 × 15
Multiply through
⇒ 2940 Joules
Thus, the gravitational potential energy is 2940 Joules
Learn more about gravitational potential energy here:
https://brainly.com/question/15896499
#SPJ1
Someone help me with these math problems please !! (It is not obligatory to put the explanation so I save time and you will answer me more quickly please!

Answers
Answer:
I don't know the selection options, so please pick them from the explanation below.
Step-by-step explanation:
"like terms" are in this contexts in one group all expressions with x, and in another group all expressions without x.
so,
3x and -2x/9
3x - 2x/9 = 27x/9 - 2x/9 = 25x/9
-1/5 ... = 124/5
... = 125/5 = 25
so, we end up with
25x/9 = 25
x/9 = 1
x = 9
14. Write a quadratic function in standard form
whose graph satisfies the given conditions.
passes through (-4,0),(2,0), and (4,40)
Answers
The standard form of the required quadratic function is y = (4/3)x² + 10x + 64/3.
What is a quadratic function?The quadratic function is defined as a function containing the highest power of a variable is two.
The standard form of a quadratic function is
y = ax² + bx + c.
The required function passes through the points (-4,0), (2,0), and (4,40)
For points (-4,0)
0 = a(-4)² + b(-4) + c
0 = 16a - 4b + c ...(i)
For points (2,0)
0 = a(2)² + b(2) + c
4 = 4a + 2b + c ...(ii)
For points (4,40)
400 = a(4)² + b(4) + c
16a + 4b + c = 40 ...(iii)
Now subtract equation (ii) from (i) and (iii)
0 - 4= 16a - 4b + c - (4a + 2b + c)
12a - 2b = -4 ....(iv)
40 - 4 = 16a + 4b + c - (4a + 2b + c)
12a + 2b = 36 ....(v)
Now add equation (iv) from (v)
12a - 2b + 12a + 2b = -4 + 36
24a = 32
a = 32 / 24
a = 4/3
Substitute the value of a = 4/3 in the equation (iv)
12(4/3) - 2b = -4
16 - 2b = -4
2b = 16 +4
b = 20 / 2
b = 10
Substitute the values of a = 4/3 and b = 10 in the equation (iii)
16(4/3) + 4(10) + c = 40
64/3 + 40 + c = 40
c = 40 - 64/3 - 40
c = 64/3
Thus, the standard form of the required quadratic function is y = (4/3)x² + 10x + 64/3.
Learn more about quadratic function here:
brainly.com/question/14083225
#SPJ1
persevere fifteen boys and fifteen girls entered a drawing for four free movie tickets. what is the probability that all four tickets were won by girls? express your answer as a fraction in simplest form.
Answers
We are given that fifteen boys and fifteen girls entered a drawing for four free movie tickets. We want to find the probability that all four tickets were won by girls.
To solve this problem, we need to consider the total number of possible outcomes and the number of favorable outcomes.
Total number of outcomes:
The total number of outcomes represents all the possible ways to choose four winners from the thirty participants (boys and girls). We can calculate this using the combination formula:
C(30, 4) = 30! / (4!(30 - 4)!) = 27,405
Here, C(n, r) represents the combination of choosing r objects from a set of n objects.
Favorable outcomes:
We want to determine the number of ways to select all four winners from the group of fifteen girls. This can also be calculated using the combination formula:
C(15, 4) = 15! / (4!(15 - 4)!) = 1365
Probability calculation:
The probability is the ratio of the favorable outcomes to the total number of outcomes. So, we divide the number of favorable outcomes by the total number of outcomes:
P(Girls winning all four tickets) = 1365 / 27,405
Simplifying the fraction, we find:
P(Girls winning all four tickets) = 1 / 20
Therefore, the probability that all four tickets were won by girls is 1/20.
In summary, out of all the possible combinations of selecting four winners from the thirty participants, only one out of every twenty combinations will result in all four tickets being won by girls.
Learn more about combination formula here : brainly.com/question/19916016
#SPJ11
4•n-7=29
1f7 less than 4 times a number is 29. Find the number.
n=number
Hn-7=29
What’s n?
Answers
Answer:
N=9
Step-by-step explanation:
4n - 7 =29
+7 +7
4n = 36
n= 9
36-7=29
expiation: i got this answer by adding 29+7 to get 36. which is also a way you can check your answer!
i hope this helps! have a wonderful day! :)
Q2) For total cost: TC(q)=10−6q+q2 determine: a. the production level (q∗) that minimizes total cost. b. The amount of Total cost for the q∗, in other words TC(q∗) ? (10 pints)
Answers
The amount of total cost at q* is 1.
To determine the production level that minimizes total cost, we need to find the value of q (production level) at which the derivative of the total cost function TC(q) is equal to zero. Let's begin by finding the derivative of TC(q):
TC(q) = 10 - 6q + q^2
To find the minimum point, we differentiate TC(q) with respect to q:
d(TC(q))/dq = -6 + 2q
Setting the derivative equal to zero and solving for q:
-6 + 2q = 0
2q = 6
q = 3
So the production level q* that minimizes the total cost is 3.
To find the amount of total cost at q*, we substitute q = 3 into the total cost function TC(q):
TC(q*) = 10 - 6(3) + (3)^2
TC(q*) = 10 - 18 + 9
TC(q*) = 1
Therefore, the amount of total cost at q* is 1.
Learn more about cost from
https://brainly.com/question/25109150
#SPJ11
Let X and Y be normal random variables with means 0 and 1, respectively, and variances 1 and 4, respectively. (a) Find P(X ≤ 1.5) and P(X ≤ -1) (b) Find the probability density function (PDF) of (Y-1)/2. (c) Find P(-1 ≤ Y ≤ 1).
Answers
The probability for the given mean and variance is given by ,
P(X ≤ 1.5) ≈ 0.9332
P(X ≤ -1) ≈ 0.1587
PDF of (Y - 1) / 2 is φ(z).
P(-1 ≤ Y ≤ 1) is approximately 0.6826
Mean = 0
Variance = 1
P(X ≤ 1.5),
Calculate the cumulative distribution function (CDF) of the normal distribution.
Use standardization by subtracting the mean and dividing by the standard deviation, evaluated at 1.5.
Z
= (X - mean) / standard deviation
= (X - 0) / 1
= X
Using the Z-score calculator, find the corresponding probability for Z ≤ 1.5, which is approximately 0.9332.
P(X ≤ 1.5) ≈ 0.9332
To find P(X ≤ -1), similarly standardize and find the probability for Z ≤ -1,
Z
= (X - mean) / standard deviation
= (X - 0) / 1
= X
Using the Z-score table or a calculator, we find the probability for Z ≤ -1 to be approximately 0.1587.
P(X ≤ -1) ≈ 0.1587
To find the probability density function (PDF) of (Y - 1) / 2,
Use the properties of linear transformations of random variables.
Let Z = (Y - 1) / 2. To find the PDF of Z,
Compute its mean and variance.
The mean of Z can be found as follows,
E[Z]
= E[(Y - 1) / 2]
= (1/2) × E[Y - 1]
= (1/2) × (E[Y] - E[1])
= (1/2) × (1 - 1)
= 0
The variance of Z can be found as follows,
Var[Z]
= Var[(Y - 1) / 2]
= (1/4) × Var[Y - 1]
= (1/4) × Var[Y]
= (1/4) × 4
= 1
Since Z follows a standard normal distribution mean 0 and variance 1,
the PDF of Z is the standard normal distribution's PDF, denoted as φ(z).
Therefore, the PDF of (Y - 1) / 2 is φ(z).
To find P(-1 ≤ Y ≤ 1), we can use the cumulative distribution function (CDF) of the normal distribution with mean 1 and variance 4.
P(-1 ≤ Y ≤ 1) = P(Y ≤ 1) - P(Y ≤ -1)
To calculate these probabilities, we need to standardize the values,
For Y ≤ 1
Z1
= (1 - mean) / standard deviation
= (1 - 1) / 2
= 0
For Y ≤ -1,
Z2
= (-1 - mean) / standard deviation
= (-1 - 1) / 2
= -1
Using the Z-score calculator, we find,
P(Y ≤ 1) ≈ 0.8413
P(Y ≤ -1) ≈ 0.1587
P(-1 ≤ Y ≤ 1)
= P(Y ≤ 1) - P(Y ≤ -1)
≈ 0.8413 - 0.1587
≈ 0.6826
P(-1 ≤ Y ≤ 1) is approximately 0.6826.
Learn more about probability here
brainly.com/question/31421202
#SPJ4
as with simple linear regression, we desire the residuals to (select all that apply)
Answers
In simple linear regression, we desire the residuals to have certain characteristics. Specifically, we want the residuals to be:
Random: The residuals should not follow a specific pattern or exhibit any systematic behavior. Random residuals indicate that the model captures the underlying relationship between the variables adequately.
1. Normally distributed: The residuals should follow a normal distribution. This assumption allows for the use of statistical inference and hypothesis testing techniques based on normality.
2. Zero mean: The average of the residuals should be close to zero. A zero mean indicates that, on average, the model is not biased and accurately represents the data.
3. Homoscedastic: The residuals should have constant variance across all levels of the independent variable. Homoscedasticity ensures that the model's performance is consistent throughout the range of values.
By satisfying these criteria, we can ensure that the model is valid, reliable, and provides accurate predictions.
Learn more about linear regression here: brainly.com/question/32505018
#SPJ11
Plot a point on the coordinate plane to represent each of the ratio values in the table.
Time (s)Distance (m)
A table displaying Time in seconds in one column and Distance in meters in the other. The time column contains 1, 2, 4, and 6. The distance column contains 3, 6, 12, and 18.
Answers
Answer:
Refer the attached graph.
Step-by-step explanation:
Given : Time (h) Distance (km) able displaying Time in hours in one column and Distance in kilometers in the other. The time column contains 1, 3, 6, and 9. The distance column contains 2, 6, 12, and 18.
To plot : The points on the coordinate plane.
Solution :
Time is independent variable so it is taken on x-axis.
Distance is taken on y-axis.
x y
1 2
3 6
6 12
9 18
When we plot these points in the coordinate plane, we get a linear equation.
The linear equation form is
Refer the attached graph.

Step-by-step explanation:
Plot a point on the coordinate plane to represent each of the ratio values in the table shows me how to point the ratio values in the table
if the frequency of q of a trait is 0.4, what is the frequency of p? responses 0.2 0.2 0.4 0.4 0.6 0.6 1
Answers
The frequency of p is equal to 1 - q, so q = 0.4, then p = 1 - 0.4 = 0.6
The frequency of p is equal to the inverse of q, so if q has a frequency of 0.4, then p has a frequency of 1 - 0.4 = 0.6. In other words, if the frequency of q is 0.4, then the frequency of p is 0.6. This means that the frequency of p is equal to 0.6, or 60%, while the frequency of q is 0.4, or 40%.
The inverse of q is the opposite of what q represents. In this case, if q has a frequency of 0.4, then this means that q appears 40% of the time. The inverse of q is 1 - 0.4, or 0.6, which means that p appears 60% of the time. Therefore, the frequency of p is equal to 0.6, or 60%, while the frequency of q is 0.4, or 40%. This means that when considering the two frequencies together, p appears 60% of the time and q appears 40% of the time.
learn more about frequency here
https://brainly.com/question/14289798
#SPJ4
A manufacturer determines that the number of toys it can sell is given by the formula
T=-4p2+160p-305, where p is the price of the toys in dollars.
At what price will the manufacturer sell the maximum number of toys and what is the maximum
number of toys that can be sold?
Answers
Answer:
The price where the manufacture sells the maximum number of toys is $20
Step-by-step explanation:
The given equation for that represents the number of toys the manufacturer can sell is given as follows;
T = -4·p² + 160·p - 305
Where;
p = The price of the toys in dollars
At the point where the manufacture sells the maxim number of toys on the graph of the equation T = -4·p² + 160·p - 305, which is the top of the graph, the slope = 0
Therefore, at the maximum point;
The slope = 0 = dT/dp = d(-4·p² + 160·p - 305)/dp = -8·p + 160
∴ -8·p + 160 = 0
160 = 8·p
8·p = 160
p = 160/8 = 20
The price where the manufacture sells the maximum number of toys is = p = 20 dollars
g gravel is being dumped from a conveyor belt at a rate of 15 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. how fast is the height of the pile increasing when the pile is 6 ft high? (round your answer to two decimal places.)
Answers
The height of the pile increasing when the pile is 6 ft high is approx 0.531 ft/min..
The volume of a cone V = (1/3)πr²h
Since we are given that h = 2r (where 2r is the diameter),
From h = 2r the value of r = h/2
Substitute the value of r in the formula of volume of cone
V = (1/3)π(h/2)²h
V = (1/3)π(h²/4)h
V = (1/12)πh³..................(1)
The rate of the volume change in time is given; it is 15 ft³/min.
Therefore
15 = dV/dt
15 = (dV/dh) · (dh/dt)
We can calculate dV/dh from the equation 1.
From the equation 1
dV/dh = (3/12)πh²
dV/dh = (1/4)πh²
Substitute the value
15 = (1/4)πh² · (dh/dt)
From the question h = 6 ft.
Substitute the value of h
15 = (1/4)π(6)² · (dh/dt)
15 = (1/4)π × 36 · (dh/dt)
15 = 9π · (dh/dt)
Divide by 9π on both side, we get
dh/dt = 15/9π
Substitute the π = 3.14
dh/dt = 15/(9 × 3.14)
dh/dt = 15/28.26
dh/dt = 0.531
At this moment, the height of the cone is increasing at the rate of 0.531 ft/min. (approximately)
To learn more about volume of a cone link is here
brainly.com/question/1984638
#SPJ4
6. (15%) Give the complexity in (g(n)) for the following five expressions ((a) to (e)). Use the simplest g(n) possible. Prove your answer for expression (a) based on the mathemat- ical definition of Big-O. (No need to give proofs for the other expressions.)
(a) √8n2+2n - 16,
(b) log(n³) + log(n²),
(c) 20-2" + 3",
(d) 7n log n + 3n15,
(e) (n+1)! +2".
Answers
(a) To determine the complexity in terms of g(n) for the expression √(8n^2 + 2n) - 16, we need to simplify it and find the dominant term.
√(8n^2 + 2n) - 16 can be rewritten as √(8n^2) * √(1 + 1/(4n)) - 16.
Ignoring the constant terms and lower-order terms, we are left with √(8n^2) = 2n.
Therefore, the complexity of expression (a) can be represented as g(n) = O(n).
Now let's discuss the complexities of the other expressions without giving formal proofs:
(b) log(n³) + log(n²):
The logarithm of a product is the sum of the logarithms. So, this expression simplifies to log(n³ * n²) = log(n^5).
The complexity of this expression is g(n) = O(log n).
(c) 20 - 2^n + 3^n:
The exponential terms dominate in this expression. Therefore, the complexity is g(n) = O(3^n).
(d) 7n log n + 3n^15:
The dominant term here is 3n^15, as it grows much faster than 7n log n. So, the complexity is g(n) = O(n^15).
(e) (n+1)! + 2^n:
The factorial term (n+1)! grows faster than the exponential term 2^n. Therefore, the complexity is g(n) = O((n+1)!).
To summarize:
(a) g(n) = O(n)
(b) g(n) = O(log n)
(c) g(n) = O(3^n)
(d) g(n) = O(n^15)
(e) g(n) = O((n+1)!)
Please note that these are simplified complexity representations without formal proofs.
Learn more about logarithm here:
https://brainly.com/question/30226560
#SPJ11
Find the work done by F over the curve in the direction of increasing t.
F = y/z i+ x/z j + x/y k; C : r(t) = t⁹i + t⁷j + t⁵k, 0 ≤ t ≤ 1
Choose the correct letter for the answer
A. W = 167/77
B. W = 0
C. W = 21
D. W = 1
Answers
Answer:
A. W = 167/77
Step-by-step explanation:
To find the work done by the vector field F over the curve C in the direction of increasing t, we can use the line integral formula:
W = ∫(F · dr)
where F is the vector field, dr is the differential vector along the curve, and the integral is evaluated over the curve C.
Given:
F = (y/z)i + (x/z)j + (x/y)k
C: r(t) = t^9i + t^7j + t^5k, 0 ≤ t ≤ 1
We need to evaluate the dot product F · dr and integrate it over the curve C.
First, we find dr:
dr = dx i + dy j + dz k
Since r(t) = t^9i + t^7j + t^5k, we can differentiate r(t) to find dr:
dr = (9t^8)i + (7t^6)j + (5t^4)k
Now, let's evaluate F · dr:
F · dr = (y/z)(dx) + (x/z)(dy) + (x/y)(dz)
Substituting the components of F and dr:
F · dr = [(y/z)(dx)] + [(x/z)(dy)] + [(x/y)(dz)]
= [(y/z)(9t^8) + (x/z)(7t^6) + (x/y)(5t^4)] dt
Next, we need to substitute the components of r(t) into the expression for F · dr:
F · dr = [(t^7/t^5)(9t^8) + (t^9/t^5)(7t^6) + (t^9/t^7)(5t^4)] dt
= (9t^16 + 7t^16 + 5t^16) dt
= 21t^16 dt
Now, we can integrate W with respect to t over the interval [0, 1]:
W = ∫(0 to 1) 21t^16 dt
= [21(t^17)/17] (0 to 1)
= (21/17)(1^17 - 0^17)
= (21/17)(1 - 0)
= 21/17
Therefore, the correct answer is:
A. W = 167/77
The work done by the vector field F over the curve C can be found using the line integral formula. Given that F = y/z i + x/z j + x/y k and C is defined by the parameterization r(t) = t⁹i + t⁷j + t⁵k for 0 ≤ t ≤ 1.
To find the work done, we need to evaluate the line integral ∫C F · dr, where F = y/z i + x/z j + x/y k and C is the curve defined by r(t) = t⁹i + t⁷j + t⁵k for 0 ≤ t ≤ 1.
First, we compute the differential of the parameterization: dr = 9t⁸i + 7t⁶j + 5t⁴k dt.
Next, we evaluate the dot product F · dr:
F · dr = (y/z)(9t⁸) + (x/z)(7t⁶) + (x/y)(5t⁴)
= (t⁷/z)(9t⁸) + (t⁹/z)(7t⁶) + (t⁹/t⁷)(5t⁴)
= 9t¹⁶/z + 7t¹⁵/z + 5t⁵
Taking the integral of F · dr over the curve C, we have:
∫C F · dr = ∫₀¹ (9t¹⁶/z + 7t¹⁵/z + 5t⁵) dt
= [((9/17)t¹⁷ + (7/16)t¹⁶ + (5/6)t⁶) / z] from 0 to 1
= (9/17z + 7/16z + 5/6) - 0
= 9/17z + 7/16z + 5/6
Since the value of z is not given, we cannot determine the exact numerical value of the work done. However, it can be concluded that the work done is in the form of (9/17z + 7/16z + 5/6), which does not match any of the given options. Therefore, none of the options A, B, C, or D is correct.
Learn more about work done here : brainly.com/question/13662169
#SPJ11