Homer Simpson finds himself in a panic attempting to meet the April 15th tax deadline. If Homer and his wife have an income of $60,000, earned $1200 in interest, invested $2500 in a tax-deferred savings plan, and have a total of $12,000 in exemptions and deductions, what would be his taxable income?
Answers
Answer:
As given, Income of Homer and his wife = $60000
Interest earned = $1200.
Adding this to total income, we have total taxable amount = 60000+1200 = $61200
Now, investment in tax deferred savings plan = $ 2500
This amount will be subtracted from total taxable income, so amount becomes = 61200-2500 = $58700
We will also subtract the exemptions and deductions = $12000
Amount becomes = 58700-12000 = $46700
Hence, Net taxable income is $46,700
Step-by-step explanation:
Related Questions
...................................................................................................

Answers
Answer:
60 in.²
Step-by-step explanation:
A = (B + b)h/2
A = (14 in. + 6 in.)(6 in.)(1/2)
A = 60 in.²
Answer:
60 in^2
Step-by-step explanation:
solution Given:
Area of the shaded region or trapezoid = Area of Rectangle ABCD - Area of triangle CDE
we have
Area of Rectangle ABCD= length* breadth =BC*AB=14*6=84 in^2
Area of Triangle CDE= 1/2* base*height=1/2*DE*CD=1/2*8*6=24 in ^2
Now
Area of the shaded region or trapezoid = Area of Rectangle ABCD - Area of triangle CDE
=84 in^2-24in^2
=60 in^2
Similarly, we have another way to calculate the area of the trapezoid;
Area = 1/2*h*(side1*side2)
=1/2*AB*(AE+BC)
=1/2*6*(6+14)
=60 in^2
The equation C=24n+2 represents the cost
Answers
Jim did not buy any tickets (n_Jim = 0).
Larry bought 7 more tickets than Jim.
To determine the number of tickets Larry bought more than Jim, we need to find the values of n for Larry and Jim's ticket purchases.
For Larry:
Let's substitute C = $170 into the equation C = 24n + 2 and solve for n:
$170 = 24n + 2
Subtracting 2 from both sides:
$168 = 24n
Dividing both sides by 24:
n = 7
For Jim:
We can calculate the number of tickets Jim bought by subtracting 12 from Larry's number of tickets:
n_Jim = n_Larry - 12
n_Jim = 7 - 12
n_Jim = -5
Since we cannot have a negative number of tickets, we can conclude that Jim did not buy any tickets (n_Jim = 0).
To find the difference in the number of tickets bought, we subtract the number of tickets Jim bought from the number of tickets Larry bought:
n_difference = n_Larry - n_Jim
n_difference = 7 - 0
n_difference = 7
Therefore, Larry bought 7 more tickets than Jim.
for such more question on quantity
https://brainly.com/question/29792134
#SPJ8
Question
The equation C=24n+2 represents the cost, C, in dollars, of buying n tickets to a play. J $170. How many more tickets did Larry buy than Jim? 12
The phone company Splint has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses 380 minutes, the monthly cost will be $173. If the customer uses 570 minutes, the monthly cost will be $249.
A) Find an equation in the form
y
=
m
x
+
b
,
where
x
is the number of monthly minutes used and
y
is the total monthly cost of the Splint plan.
Answer:
y
=
B) Use your equation to find the total monthly cost if 942 minutes are used.
Answer: If 942 minutes are used, the total cost will be
dollars.
Answers
The solution of the given problem of equation comes out to be total cost for 942 minutes is $1044.
What is an equation?The similar symbol (=) is used in arithmetic equations to signify equality between two statements. It is shown that it is possible to compare various numerical factors by applying mathematical algorithms, which have served as expressions of reality. For instance, the equal sign divides the number 12 or even the solution y + 6 = 12 into two separate variables many characters are on either side of this symbol can be calculated. Conflicting meanings for symbols are quite prevalent.
Part A:
Given:
customer uses 380 minutes, the monthly cost will be $173.customer uses 570 minutes, the monthly cost will be $249.To find an equation,
Where x is number of monthly minutes.
and y is total monthly of splint plan.
So, equation is:
\(\rightarrow \text{y} =\text{mx} +\text{b}\)
For the first case:
\(\rightarrow\bold{173 = 380x + b}\)
Second case:
\(\rightarrow\bold{249= 570x + b}\)
Solve for x:
\(\rightarrow{173 - 380\text{x}=249- 570\text{x}\)
\(\rightarrow{-207=-321\)
\(\rightarrow \text{x} =\dfrac{321}{207}\)
\(\rightarrow \text{x} =\dfrac{107}{69}\)
\(\rightarrow \text{x} \thickapprox1.55\)
For value of b
\(\rightarrow 173 = 380(1.55) + \text{b}\)
\(\rightarrow 173 - 589 = \text{b}\)
\(\rightarrow -416 = \text{b}\)
Part B:
\(\rightarrow \text{y} = 942(1.55) - 416\)
\(\rightarrow \text{y} = 1460.1 - 416\)
\(\rightarrow \text{y} \thickapprox1044\)
Therefore, the solution of the given problem of equation comes out to be total cost for 942 minutes is $1044.
To know more about the equation, visit:
https://brainly.com/question/29657983
Is this correct or not?
If not please provide correct answer

Answers
Answer:
It is correct please I do not want yo sound rude can you give me brainliest answer.
Answer:
correct steps
Step-by-step explanation:
if asked to find angles in terms of the ratios, then don't forget to shift sin / cos / tan across the equal sign and change it to arc sin / cos / tan.
Write the quadratic function in vertex form, then identify the vertex
h(x)=x^2+20x+90
h(x)=
Vertex:
I need this answered ASAP please !

Answers
Answer:
vertex = (- 10, - 10 )
Step-by-step explanation:
The equation of a quadratic in vertex form is
y = a(x - h)² + k
where (h, k ) are the coordinates of the vertex and a is a multiplier
To obtain this form use the method of completing the square.
Given
h(x) = x² + 20x + 90
add/subtract ( half the coefficient of the x- term )²
h(x) = x² + 2(10)x + 100 - 100 + 90
= (x + 10)² - 10 ← in vertex form
with (h, k ) = (- 10, - 10 )
Write the equation of the line that goes through the points A(3,-2) and B(5,4)
Answers
Answer:
y = 3x - 11
Step-by-step explanation:
(3, -2) and (5, 4)
m = 4+2/5-3
m = 6/2
m = 3
y = 3x + b
4 = 3(5) + b
4 = 15 + b
b = -11
y = 3x - 11
is 2x^2+y =3x - 1 a function quadratic
Answers
Answer:
Step-by-step explanation: yes because when rewritten in standard form the x term will still be raised to the 2nd power.
James wants to earn money by selling cold water bottles. He buys a pack that costs $8.00. He plans to charge $2.00 for each bottle of water he sells. Calculate the amount of profit James will make if sells 24 water bottles.
Answers
Subtract 7 from each side.Divide each side by 3.Add 7 to each side.Multiply each side by 3.

Answers
Given:
\(\frac{h}{3}+7=5\)Required:
To find the second step in solving the given equation.
Explanation:
Consider
\(\frac{h}{3}+7=5\)The first step is, subtract 7 on both side.
\(\begin{gathered} \frac{h}{3}+7-7=5-7 \\ \\ \frac{h}{3}=-2 \end{gathered}\)The second step is, multiply each side by 3.
\(\begin{gathered} \frac{h}{3}\times3=-2\times3 \\ \\ h=-6 \end{gathered}\)Final Answer:
The second step is multiply each side by 3.
i need help asap
than you!

Answers
The highest height for the daily rainfall were for 5 and 6 inches
How to Interpret Dot Plots?Dot plots are used to present data in the form of points or small circles. It is similar to a simplified histogram or bar graph in that the height of the bar made up of points represents the numerical value of each variable. Dot plots are used to represent small amounts of data.
From the given dot plot, we see the number of times for each height of rainfall.
Thus, we see that the highest number of times of rainfall height was from that of 5 and 6 inches.
Thus, we conclude those were the highest heights for the daily rainfall.
Read more about Dot plots at: https://brainly.com/question/24309209
#SPJ1
The business college computing center wants to determine the proportion of business students who have personal computers (PC's) at home. If the proportion differs from 30%, then the lab will modify a proposed enlargement of its facilities. Suppose a hypothesis test is conducted and the test statistic is 2.5. Find the P-value for a two-tailed test of hypothesis.
Answers
The probability of observing such an extreme result by chance alone is 0.0124.
To find the P-value for a two-tailed test of hypothesis, we need to first determine the significance level (alpha) of the test. Let's assume a significance level of 0.05, which is a common choice.
Since this is a two-tailed test, we need to find the probability of observing a test statistic as extreme or more extreme than 2.5 in either direction. We can find this probability using a standard normal distribution table or a calculator.
Using a standard normal distribution table, we can find that the probability of observing a z-score of 2.5 or greater is 0.0062. The probability of observing a z-score of -2.5 or smaller is also 0.0062. Therefore, the P-value for the two-tailed test of hypothesis is:
P-value = 2 * 0.0062
P-value = 0.0124
This means that if the true proportion of business students who have personal computers at home differs from 30%, with a significance level of 0.05, and we obtain a test statistic of 2.5, then the probability of observing such an extreme result by chance alone is 0.0124.
To learn more about Probability :
brainly.com/question/24756209
#SPJ11
For each of the number lines, write an absolute value equation that has the solution set -4 and -8

Answers
The absolute value equation that has the solution set is |x + 6| = 2
How to write the absolute value equation that has the solution setFrom the question, we have the following parameters that can be used in our computation:
Solution set = -4 and -8
The midpoint of the above solution is
c = (-4 - 8)/2
So, we have
c = -6
So, we have
|x + 6| = d
Using any of the points, we have
|-4 + 6| = d
Evaluate
d = 2
So, we have
|x + 6| = 2
Hence, the absolute value equation that has the solution set is |x + 6| = 2
Read more about absolute value equation at
https://brainly.com/question/26954538
#SPJ1
Which expression shows the result of applying the distributive property to 3(1/5x - 1/7)?
O 3/5 x - 3/7
O - 3/5 x - 3/7
O - 3/5 x + 3/7
O 3/5 x + 3/7 PLEASE HELP WILL GIVE BRAINIEST
Answers
Answer:
3/5x - 3/7
Do let me know if you need any clarification :)

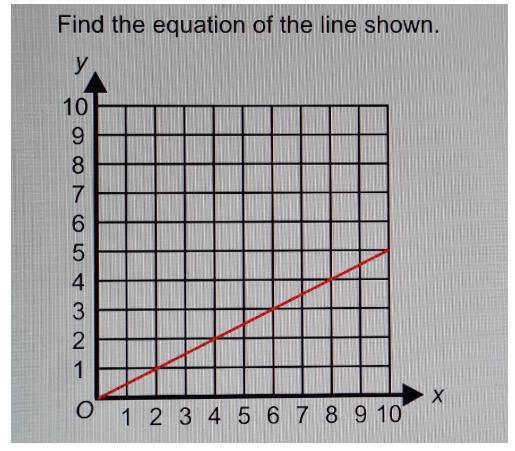
Find the equation of the line shown.
I need it quick pls
Answers
The equation of the line shown is y = 2x.
What is a proportional relationship?In Mathematics, a proportional relationship can be defined as a type of relationship that generates equivalent ratios and it can be modeled or represented by the following mathematical expression:
y = kx
Where:
x and y represents the variables or data points.k represents the constant of proportionality.Next, we would determine the constant of proportionality (k) as follows:
Constant of proportionality, k = y/x
Constant of proportionality, k = 2/1 = 4/2
Constant of proportionality, k = 2.
Therefore, the required equation is given by:
y = kx
y = 2x
Read more on proportional relationship here: brainly.com/question/28350476
#SPJ1
PLEASE ANSWER QUICK, ITS URGENT!

Answers
Step-by-step explanation:
which part of the question do you need
find the slope of the line that passes through the points (3,0) and (-11,-15) ✨
Answers
Answer:
m=15/14
Step-by-step explanation:
Find an ordered pair (x, y) that is a solution to the equation.
3x-y=6
Answers
For example, if we let x = 2, then:
3x - y = 6
3(2) - y = 6
6 - y = 6
-y = 0
y = 0
So, when x = 2, y = 0, and the ordered pair (2, 0) is a solution to the equation 3x - y = 6.
What are the solutions to x³ = -2 – 2i in polar form?
Answers
Therefore, the solutions to x³ = -2 - 2i in polar form are x₁ = √6 + √2i, x₂ = -√2 + √6i, and x₃ = -√6 - √2i.
What is complex number?A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, defined as the square root of -1. The real part of the complex number is a, and the imaginary part is bi. Complex numbers are often used in mathematics and engineering to represent quantities that involve both a real part and an imaginary part, such as electrical impedance, wave functions, and solutions to polynomial equations. Complex numbers can be added, subtracted, multiplied, and divided using rules similar to those for real numbers, and they can be plotted in a two-dimensional coordinate system called the complex plane, with the real part along the x-axis and the imaginary part along the y-axis.
Here,
To find the solutions to the equation x³ = -2 - 2i in polar form, we first convert the complex number -2 - 2i to polar form:
|-2 - 2i| = sqrt((-2)^2 + (-2)^2) = 2*sqrt(2)
arg(-2 - 2i) = tan⁻¹((-2)/(-2)) = tan⁻¹(1) = π/4 (in the second quadrant)
So, -2 - 2i in polar form is 2√2∠(π/4).
Next, we can write x³ in polar form as |x³|∠(3θ), where |x³| = |x|³ and 3θ is the angle formed by rotating θ three times. So we have:
|x³| = |-2 - 2i| = 2*sqrt(2)
3θ = arg(-2 - 2i) + 2kπ, where k is an integer
Substituting the value of arg(-2 - 2i), we have:
3θ = π/4 + 2kπ
Dividing both sides by 3, we get:
θ = π/12 + (2kπ)/3
So the three solutions in polar form are:
x₁ = 2√2∠(π/12)
x₂ = 2√2∠(5π/12)
x₃ = 2√2∠(9π/12)
Simplifying, we have:
x₁ = √6 + √2i
x₂ = -√2 + √6i
x₃ = -√6 - √2i
To know more about complex number,
https://brainly.com/question/20566728
#SPJ1
Figure ABCD is a parallelogram
A
B
D
C
Which transformations will carry figure ABCD onto itself?
Select all that apply.
A
A 180° rotation about the midpoint of AB.
B. A 360° rotation about the midpoint of AB.
C.
A reflection about the line joining the midpoints of AB and DC
D. A reflection about the diagonal AC
E A 180° rotation about the intersection of the two diagonals of ABCD
Answers
Answer:
A. A 180 degree rotation about the midpoints of AB.
Step-by-step explanation:
The rotation of a shape less than 360 degrees will carry the figure onto itself. A parallelogram is a rectangular shape which is slight diagonal shaped. The parallelogram will carry transformation when its rotation is about 180 degrees.
assume that x is uniformly distributed on [0,3]. using the central limit theorem, find the shortest interval (around hn) that has 95% probability of containing the true value of h. (such an interval is known as 95% confidence interval for h).
Answers
The probability density function (pdf) for the uniform distribution has the basic formula: f(x) = 1/ (B-A) for A x B.
A continuous probability distribution, the uniform distribution is concerned with equally likely outcomes. It is referred to as having a rectangular distribution on the interval [a,b] or having a uniform distribution for the continuous random variable X. Above is a representation of the probability density function of a continuous uniform distribution. The probability of drawing a heart, club, diamond, or spade is equally likely; hence, the area under the curve is 1, which makes sense given that the total of all probabilities in a probability distribution is 1.
Learn more about uniform here-
brainly.com/question/28841819
#SPJ4
$46 for 5 toys
$ / toy
Answers
Answer:
$9.20 for 1 toy
Step-by-step explanation:
If it's $46 for 5 toys, we can divide both $46 and 5 to get $9.20 for 1 toy.
Evaluate Piecewise Functions. (Everything you need to know is in the photo. You can also use the word "undefined" next to the answer only if necessary).

Answers
Answer:
f(-1) = 6
Explanation:
Looking at the piecewise function given, we see that
f(x) = -3x -5
for x different from -1
And
f(x) = 6
for x = -1
So, we choose the suitable one, since x = -1
Mariana and her best friend are attending a concert in a large auditorium. They just climbed up 125 steps. The number of steps they climbed can be represented by
zero
positive
negative
Answers
The number of steps they climbed can be represented by positive
How to represent the number of steps?From the question, we understand that they climbed up
Upward movements are usually represented by the positive sign
This means that:
Steps = 125 or +125
Hence, the number of steps they climbed can be represented by positive
Read more about positive numbers at
https://brainly.com/question/1782403
#SPJ1
Graph t > -3 on the number line.

Answers
Answer:
Read explanation
Step-by-step explanation:
t is greater than -3. This means it doesn't include -3 itself. So place an open dot at -3 on the number line, with the arrow pointing right because the inequality is greater than [-3].
Match each expression with A, B, C or D.
A=a^3
B=6a
C=12a
D=3a^2
i)3a x 4
ii)a^2xa
iii) 6 1/2 a^2

Answers
The matching expressions are:
\(i) 3a x 4 = C (12a)\\ii) a^2 x a = A (a^3)\\iii) 6 × 1/2 a^2 = D (3a^2)\)
i) 3a x 4 can be represented as C (12a) since multiplying 3a by 4 gives 12a.
ii) a^2 x a can be represented as A (a^3) since multiplying a^2 by a gives a^3.
iii) \(6 \times 1/2 a^2\) can be represented as D (3a^2) since multiplying 6 by 1/2 and then by a^2 gives 3a^2.
To understand the matching expressions, let's break down each one:
i) 3a x 4:
This expression represents multiplying a variable, 'a', by a constant, 4. The result is 12a, which matches with C (12a).
ii) a^2 x a:
This expression represents multiplying the square of a variable, 'a', by 'a' itself. This results in a^3, which matches with A (a^3).
iii) 6 × 1/2 a^2:
This expression involves multiplying a constant, 6, by a fraction, 1/2, and then multiplying it by the square of 'a', a^2. The final result is 3a^2, which matches with D (3a^2).
Therefore, the matching expressions are:
i) 3a x 4 = C (12a)
ii) a^2 x a = A (a^3)
iii) 6 × 1/2 a^2 = D (3a^2)
for such more question on matching expressions
https://brainly.com/question/12270624
#SPJ8
Find the sum and express it in simplest form.
(-6b²2b-1) + (-2b² + 4b)
100
Clear all
Enter the correct answer.
000
DONE
Answers
Answer:
-8b^2 + 4b
Step-by-step explanation:
To simplify the expression (-6b^2 2b-1) + (-2b^2 + 4b), we need to combine like terms.
First, let's distribute the negative sign to the terms inside the first set of parentheses:
(-6b^2) + (-2b^1) = -6b^2 - 2b^1
Now let's combine the terms inside the second set of parentheses:
(-2b^2) + (4b) = -2b^2 + 4b
Finally, let's add the two expressions:
(-6b^2 - 2b^1) + (-2b^2 + 4b) = -6b^2 - 2b^1 - 2b^2 + 4b
Simplifying, we get:
-8b^2 + 4b = -8b^2 + 4b
The final simplified expression is: -8b^2 + 4b.
A car’s gas tank will hold 24 gallons when full. The car’s tank is presently 1/3 full. How much more gas will it take to fill the tank?
Answers
The additional gas it will take to fill the tank is 16 gallons
How much more gas will it take to fill the tank?From the question, we have the following parameters that can be used in our computation:
Capacity = 24 gallons
Current volume = 1/3 full
This means that
Remaning volume = 1 - 1/3
Evaluate
Remaning volume = 2/3
The additional gas it will take to fill the tank is
Additional = 2/3 * 24
Evaluate
Additional = 16
Hence, the additional gas it will take to fill the tank is 16 gallons
Read more about proportion at
https://brainly.com/question/12024093
#SPJ1
When an object is weighed on a scale, the number displayed may vary from the object’s actual weight by at most 0.4 pounds. The scale says the object weighs 125.8 pounds. Part A: Write an absolute value inequality that describes the range of the actual weight of the object. Use the variable w to represent the actual weight of the object. Part B: Solve the absolute value inequality for w. Express your answer as a compound inequality.
Answers
The compound inequality that represents the range of the actual weight of the object is 125.4 ≤ w ≤ 126.2.
Part A: The absolute value inequality that describes the range of the actual weight of the object is:
|w - 125.8| ≤ 0.4
Part B: To solve the absolute value inequality, we can break it down into two separate inequalities:
w - 125.8 ≤ 0.4 and - (w - 125.8) ≤ 0.4
Solving the first inequality:
w - 125.8 ≤ 0.4
Add 125.8 to both sides:
w ≤ 126.2
Solving the second inequality:
-(w - 125.8) ≤ 0.4
Multiply by -1 and distribute the negative sign:
-w + 125.8 ≤ 0.4
Subtract 125.8 from both sides:
-w ≤ -125.4
Divide by -1 (note that the inequality direction flips):
w ≥ 125.4
Combining the solutions, we have:
125.4 ≤ w ≤ 126.2
The object is 125.4 ≤ w ≤ 126.2.
for more questions on compound
https://brainly.com/question/3989769
#SPJ8
A company is producing picture frames as well as the glass for the front of the frames. The amount of wood required
for the frame is represented by the function W/(x), and the amount of glass is represented by the function G(x). The
frames have lengths represented by the function f(x) and widths represented by g(x).
X
2
3
4
5
W(x)=2[(f+g)(x)]
14
24
34
44
G(x) = (f-g)(x)
6
27
60
105
Which statement describes the combined functions W(x) and G(x)?
O The amount of glass required has a constant rate of change, but the amount of wood does not.
O The amount of wood required has a constant rate of change, but the amount of glass does not.
O Both the amount of wood required and the amount of glass required have a constant rate of change.
ONeither the amount of wood required nor the amount of glass required has a constant rate of change.
Answers
Answer:The combined functions W(x) and G(x) represent the amount of wood and glass required to produce a picture frame. Based on the information provided,
W(x)= 2[(f+g)(x)] and G(x) = (f-g)(x)
By looking at the values of the given table, it can be observed that the rate of change in the amount of glass required (G(x)) is not constant, it increases as x increases.
On the other hand, the rate of change in the amount of wood required (W(x)) is not constant as well, it increases as x increases too.
It's not mentioned any information about constant rate of change for f and g.
Therefore, the correct statement that describes the combined functions W(x) and G(x) is: "Neither the amount of wood required nor the amount of glass required has a constant rate of change."
It's important to mention that the problem provided does not have a unique solution, because the values for f and g are not defined so it's not possible to infer their behaviour over time.
It is only possible to infer the behaviour of the functions W(x) and G(x) given the information provided, and it is clear that the rate of change for both functions does not remain constant, but it increases as x increases.
Step-by-step explanation:
Jessie designed a sculpture that is shaped like a circle. The circumference of the sculpture is π meters.
Which measurement is closest to the area of the sculpture in square meters?
31.4 m²
78.5 m²
62.8 m²
314 m²
Answers
The required area of the sculpture that is shaped like a circle is \(78.5m^2\).
Given that,
Jessie designed a sculpture that is shaped like a circle,
The circumference of the sculpture is 10π meters.
We have to determine,
Which measurement is closest to the area of the sculpture in square meters.
According to the question,
Circumference of the circle = \(2\pi r\)
Where, circumference = \(10\pi\)
Then,
\(10\pi =2\pi r\)
\(r=\frac{10\pi }{2\pi }\)
\(r=5m\)
Therefore,
Jessie designed a sculpture that is shaped like a circle.
Area of the circle = \(\pi r^2\)
Where, r = 5m
Then,
Area of the circle is given by,
\(=\pi r^2\)
\(=3.14\) × \((5)^2\)\(=3.14\) × \(25\)\(=78.5m^2\)
Hence, The required area of the sculpture that is shaped like a circle is \(78.5m^2\).
To know more about Circle click the link given below.
https://brainly.com/question/20908820