Answers
Answer:
12>7
Step-by-step explanation:
4x -3= 4x*3
4x*3= 12x
12x< 7
12> 7
I think this is right im not 100% sure thouh
Related Questions
a big is a full of candies and the following data is provided: the lower specification limit is 48 pound and upper specification limit is 56 pound, the population mean weight of the candy bag is 50 pound with a standard deviation of 1.75 pound. (normal distribution exist) (8pts) a) what percentage of the bag contain less than 48 pound? (4 pts) b) what would be average weight of the bag if we desire 4% of the bag to be below 48 pound (4 pts)
Answers
12.65% of the bag contains less than 48 pounds. 44.94 is the average of the bag if we desire 4% of the bag to be below 48 pounds.
As per the given question,
Lower specification limit = 48 poundsUpper specification limit = 56 poundsThe mean weight of the candy bag = 50 poundsThe Standard Deviation of the candy bag = 1.75 pounds.⇒ The z-value at 48 = ( Value - mean ) / Standard deviation
= ( 48 - 50 ) / 1.75
= ( -2 ) / 1.75
= -1.142857143
∴ p( z-value ) = 0.1265 ≅ 12.65% ( using Normsinv )
⇒ z-value( 0.04 ) = -1.75069 ( using Normsinv( 0.04 ) )
∵ The z-value at 48 = ( Value - mean ) / Standard deviation
⇒ -1.75069 = ( 48 - Mean ) / 1.75
⇒ Mean = ( -1.75069 × 1.75 ) + 48
= ( -3.0637075 ) + 48
∴ Mean = 44.9362925 ≅ 44.94
Therefore, The percentage of bag that contains less than 48 pounds is 12.65% and the average weight of the bag if we desire 4% of the bag to be below 48 pounds is 44.94.
To know more about mean using z-value refer to:
https://brainly.com/question/28074946
#SPJ4
In AUVW, the measure of ZW=90°, the measure of ZU=61°, and VW =
3 feet. Find the length of UV to the nearest tenth of a foot.
Answers
The length of the UV is 3.7 feet.
Right Triangle:All triangles have interior angles adding to 180°. When one of those interior angles measures 90°, it is a right angle and the triangle is a right triangle. In drawing right triangles, the interior 90° angle is indicated with a little square □ in the vertex.
In ΔUVW , The sides and angles are :
∠W = 90°
∠U = 61°
VW = 3 feet.
Let, taking UV be x
So, Accordingly to right angle triangle,ΔUVW
Sin ∠U = \(\frac{VW}{UV}\)
Sin 61° = \(\frac{3}{x}\)
Sin 61° ≈ 0.87
Plug the values in above formula:
x = \(\frac{3}{0.87}\)
x = 3.7
Learn more about Triangle at:
https://brainly.com/question/29083884
#SPJ4
Please help! :)
Will give brainliest, thank you

Answers
Answer:
y=-3/5x+2
Step-by-step explanation:
slope is -3/5
starting point is 2
Which of the following numbers is irrational?
OA) -7.8 repeating
OB) 25
OC) 25.8125
OD 0.025
Answers
The rest can be solved as rational. Negative numbers are not rational.
Answer:
OA) -7.8 repeating... is irrational number
Step-by-step explanation:
I. Repeating Decimal is on of irrational number
II. Pie.value is also irrational number, but in computer science, we can find pie value with the quantum computer.
Can someone help me with this math homework please!
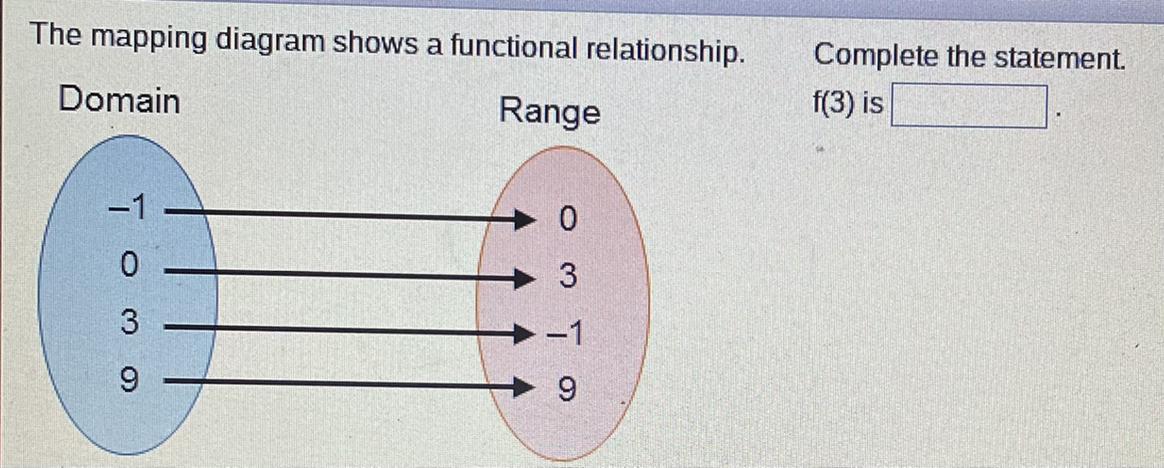
Answers
Answer:
-1
Step-by-step explanation:
we match the input to the output to find that f(3) points towards -1
Which answer choice gives three lengths that WILL form a triangle when put together?
Answers
Using the side length property of the triangle, which is called the triangle inequality theorem, we found that none of the choices will form a triangle.
What is a triangle?
A triangle is a polygon with three vertices and three sides. The angles of the triangle are formed by the connection of the three sides end to end at a point. The triangle's three angles add up to 180 degrees in total. Any three locations that are not collinear provide a distinct triangle and a distinct plane.
The options given in the question are:
a)5,7,13
b) 12, 18, 35
c) 107,8,9
d) 4,5,10
One of the properties of the length of the sides of a triangle is as follows:
The sum of the length of any two sides of a triangle should be always greater than the third side.
Using this property, we can find which sides can be used to form a triangle.
a) 5 + 7 = 12
12 is not greater than 13.
So this cannot form a triangle.
b) 12+18 = 30
30 not greater than 35.
So this cannot form a triangle.
c) 8+9 = 17
17 not greater than 107.
So this cannot form a triangle.
d) 4+5 = 9
9 is not greater than 10.
So this cannot form a triangle.
Therefore using the side length property of the triangle, which is called the triangle inequality theorem, we found that none of the choices will form a triangle.
To learn more about triangles, follow the link.
https://brainly.com/question/30115347
#SPJ1
Scenario 2 Magnifi Co. produces a high-end amplifier for musical aficionados. Historically, only 85% of the 200 amplifiers produced per month on average have met the company's demanding standards for
Answers
Scenario 2 Magnifi Co. produces a high-end amplifier for musical aficionados. Historically, only 85% of the 200 amplifiers produced per month on average have met the company's demanding standards for quality control. Suppose a random sample of 50 amplifiers is taken from a month's production..
What is the probability that less than 40 of the amplifiers will meet the company's quality standards? b) What is the probability that between 40 and 45 inclusive of the amplifiers will meet the company's quality standards? c) What is the probability that more than 45 of the amplifiers will meet the company's quality standards? a) In order to solve for the probability that less than 40 amplifiers will meet the company's quality standards, we can use the binomial distribution formula: P(X < 40) = Σi=0^39 C(50, i) (0.85)i(1-0.85)50-i
This can be solved using a computer, calculator, or by using a binomial probability table. Using a binomial table, we can find that P(X < 40) = 0.024. Therefore, there is a 0.024 probability that less than 40 amplifiers will meet the company's quality standards. b) To solve for the probability that between 40 and 45 amplifiers inclusive will meet the company's quality standards, we can use the binomial distribution formula again. We need to solve for P(40 ≤ X ≤ 45): P(40 ≤ X ≤ 45) = Σi=40^45 C(50, i) (0.85)i(1-0.85)50-i This can also be solved using a computer, calculator, or binomial table. Using a binomial table, we can find that P(40 ≤ X ≤ 45) = 0.435. Therefore, there is a 0.435 probability that between 40 and 45 amplifiers inclusive will meet the company's quality standards. c) To solve for the probability that more than 45 amplifiers will meet the company's quality standards, we can use the binomial distribution formula one more time. We need to solve for P(X > 45): P(X > 45) = Σi=46^50 C(50, i) (0.85)i(1-0.85)50-i Once again, this can be solved using a computer, calculator, or binomial table. Using a binomial table, we can find that P(X > 45) = 0.056. Therefore, there is a 0.056 probability that more than 45 amplifiers will meet the company's quality standards.Overall, it can be concluded that the probability that less than 40 amplifiers will meet the company's quality standards is low, the probability that between 40 and 45 amplifiers inclusive will meet the company's quality standards is relatively high, and the probability that more than 45 amplifiers will meet the company's quality standards is relatively low.
To know more about amplifier visit:
https://brainly.com/question/32812082
#SPJ11
a connected graph has nine vertices and twelve edges. does it have a circuit? why or why not? the graph has a circuit because a connected graph with n
Answers
Yes, it does have a circuit. This is because a connected graph with nine vertices and twelve edges is guaranteed to have at least one circuit.
A circuit is a path that starts and ends at the same vertex while visiting all other vertices exactly once. A connected graph with n vertices and 2n edges is guaranteed to have at least one circuit. This is because each edge in the graph contributes to two paths (one in each direction), and the total number of paths must be equal to the number of edges. Since a graph with nine vertices and twelve edges has more edges than vertices, it is guaranteed to have at least one circuit. Therefore, the graph does indeed have a circuit.
The complete question is : a connected graph has nine vertices and twelve edges. does it have a circuit? why or why not? the graph has a circuit because a connected graph with n vertices and 2n edges is guaranteed to have at least one circuit.
Learn more about graph here
https://brainly.com/question/17267403
#SPJ4
What would 3/7 x 14 = ?
Please show work if you are able too! :)
Answers
Explanation:
You want to put the 14 over 1 so that you’re working with 2 fractions.
After that you’re able to divide the 7 and 14 by 7. That will leave you with 3 times 2.

Find the missing length in a figure.

Answers
Answer:
5 cm
Step-by-step explanation:
Opposite sides are equal in a rectangle.
So, Area of missing length = 16-11 = 5 cm

25 points!!!!!!!!!!!!!!!!!!

Answers
Answer:
cos 32° = 12/x
x = 14.15
Step-by-step explanation:
What is the value of x ?

Answers
Answer:
61°
Step-by-step explanation:
For parellel lines cut by a transversal corresponding angles are equal.
what is the probability that 113 or fewer people in this sample have had chickenpox in their childhood? (round your answer to four decimal places.)
Answers
The answer to the probability that 113 or fewer people in this sample have had chickenpox in their childhood is 0.1422
The probability that 113 or fewer people in this sample have had chickenpox in their childhood is 0.1422(rounded to four decimal places).
Step-by-step explanation : We can use the binomial probability formula to solve this problem. Let's assume p be the probability that a person had chickenpox in their childhood. q = 1 - p is the probability that a person did not have chickenpox in their childhood. n is the sample size which is 400. The formula is as follows:P(X ≤ 113) = P(X = 0) + P(X = 1) + ... + P(X = 113)P(X = k) = C(n, k) * p^k * q^(n-k) where C(n, k) is the combination of n objects taken k at a time which is given by n!/k!(n-k)! Substituting the values of n, p, q, and k in the formula we get, P(X ≤ 113) = ∑ C(400, k) * p^k * q^(n-k) , for k = 0 to k = 113.
We can calculate the probability using a calculator or Microsoft Excel.
Using the Excel formula = BINOM.DIST(113,400,0.17,TRUE) we get the answer as 0.1422(rounded to four decimal places).Therefore, the probability that 113 or fewer people in this sample have had chickenpox in their childhood is 0.1422 (rounded to four decimal places).
To know more about probability refer here :
https://brainly.com/question/30034780#
#SPJ11
Problem of Tartaglia (1500-1577): among all positive numbers a, b whose sum is 8, find those for which the product of the two numbers and their difference is largest. (Enter your answers as a comma-separated list.)
a, b = _____
Let x = a - b and express abx in terms of x alone.
Answers
As per the information provided, a = 4√3/3 + 4, b = 4 - 4√3/3 the answer can be calculated with optimization method. it will be as follows:
Sum of a and b is 8, we get
a+b=8
b=8−a
Now, let x=a−b
Then we get,
\(x=a−(8−a) \\ x=2a−8 \\ x+8=2 \\ 1 \div 2x+4=a
\)
we use this to answer to solve for b
\(b=8−a \\ =8−(1 \div 2x+4) \\ =4−1 \div 2x
\)
Now we use the product of two numbers and its difference. This can be expressed as:
\(a⋅b⋅x=(1 \div 2x+4)(4−1 \div 2x) \\ x=2 {x}^{2} − \frac{1}{4} {x}^{3} +16x−2x^{2} \\ =−14x^{3} +16x
\)
Thus, this expression that we need to maximize. Take the derivative, set it equal to zero, and solve for x
\(−3 \div 4x ^{2} +16=0 \\ 16 =3 \div 4 x ^{2} \\ 643=x \\ 28√3 \div 3=x\)
Now for us to check that this is a maximum, we have to note that the second derivative is
\(−3 \div 2x
\\ At \\
x=8√3 \div 3
\)
the second derivative is −4√3. Since this number is negative, the point is a maximum.
Now we must find the values of a and b for this x. We have to use the relationship
\(a=1 \div 2x+4\)
\(a=1 \div 2 \times 8√3 \div 3+4 \\ =4√3 \div 3+4\)
now we use the relationship b=8−a
\(b=8−(4√3 \div 3+4) \\ =4−4√3 \div 3\)
The first step in determining a function's maximum or minimum value is differentiating it. Then, set this derivative to zero and conduct the computation.
x. This will reveal the location of a function's maximum or minimum, but it won't reveal which.
Take the second derivative to get more details. A local maximum occurs when both the first and second derivatives are negative. You have a local minimum when both the first derivative and the second derivative are zero.
To learn more about optimization: https://brainly.com/question/28970005
#SPJ4
In an arithmetic sequence, a_(4)=19 and a_(7)=31. Determine a formula for a_(n), the n^(th ) term of this sequence.
Answers
To determine a formula for the n-th term of an arithmetic sequence, we need to find the common difference (d) first.
The common difference is the constant value that is added or subtracted to each term to get to the next term.
In this case, we can find the common difference by subtracting the fourth term from the seventh term:
d = a₇ - a₄
d = 31 - 19
d = 12
Now that we have the common difference, we can use it to find the formula for the n-th term of the arithmetic sequence. The formula is given by:
aₙ = a₁ + (n - 1)d
In this formula, aₙ represents the n-th term, a₁ represents the first term, n represents the position of the term, and d represents the common difference.
Since we don't have the first term (a₁) given in the problem, we can find it by substituting the known values for a₄ and d:
a₄ = a₁ + (4 - 1)d
19 = a₁ + 3(12)
19 = a₁ + 36
a₁ = 19 - 36
a₁ = -17
Now we can substitute the values of a₁ and d into the formula to get the final formula for the n-th term:
aₙ = -17 + (n - 1)(12)
Therefore, the formula for the n-th term (aₙ) of the given arithmetic sequence is aₙ = -17 + 12(n - 1).
Learn more about Arithmetic sequence here -: brainly.com/question/30194025
#SPJ11
If a hypothesis test leads to the rejection of the null hypothesis, a _____ have been committed.
Answers
If a hypothesis test leads to the rejection of the null hypothesis, a Type I error has been committed.
Type I error:
Rejecting the null hypothesis when it is in fact true is a Type I mistake. It entails drawing conclusions about outcomes that are statistically significant when, in fact, they were just the consequence of chance or unrelated causes.
The significance level you select (alpha or ) determines the likelihood that you will make this mistake. You determined that figure at the start of your research to determine the statistical likelihood of getting your results (p value).
The typical significance level is 0.05 or 5%. If the null hypothesis is accurate, your results only have a 5% chance or less of occurring.
A Type I error has been made if a hypothesis test results in the rejection of the null hypothesis.
To learn more about hypothesis test click here:
brainly.com/question/17099835
#SPJ4
Can you please help my brother !!!!!!

Answers
Answer:
5/4 = 5/8 times 2
1
2
4
5
7
16/5 = 8 times 2/5
9 and 8 the last two
Step-by-step explanation:
Factor expressions x^2+4x+4
Answers
Answer:
Your answer is:
(x+2)^2
Factor x2+4x+4
x2+4x+4
The middle number is 4 and the last number is 4.
Add together to get 4
Multiply together to get 4
2+2 = 4
2*2 = 4
(x+2)(x+2) or (x+2)^2
Find the area of the front face of the shed. Please help asap.

Answers
Answer:
8.25cm²
Step-by-step explanation:
the area of the triangle = (half x base x height )=
(1.5x3)÷2= 2.25cm²
the area of the rectangle= length x width = 3x2= 6cm²
total = 2.25+6= 8.25cm²
_____________are the most powerful computers at any given time, but are built especially for assignments that require arithmetic speed.
Answers
Supercomputers are the most powerful computers at any given time, but are built especially for assignments that require arithmetic speed.
The supercomputers, which are the most advanced and high-performance computers available, are specifically constructed to handle assignments that demand rapid arithmetic processing.
These machines are optimized for executing complex mathematical operations and simulations, enabling them to tackle problems that require immense computational power.
By harnessing parallel processing, massive memory capacities, and specialized architectures, supercomputers excel in solving scientific, engineering, and research challenges that necessitate exceptional arithmetic speed.
Their capabilities contribute to advancements in various fields, including weather forecasting, molecular modeling, astrophysics, and cryptography.
For more questions like Supercomputers click the link below:
https://brainly.com/question/30227199
#SPJ11
The graphs of the functions f and g are shown in the figure.
The x y coordinate plane is given. There are 2 functions on the graph.
The function labeled f consists of 3 line segments. Function f begins at the point (−2, 0.5), goes linearly down and right to the origin where it sharply changes direction, goes linearly up and right, passes through the point (1, 2), sharply changes direction at the point (2, 4), goes linearly down and right, passes through the point (5, 3), and ends approximately at the point (7, 2.3).
The function labeled g consists of 2 line segments. Function g begins at the point (−2, 4), goes linearly down and right, passes through the point (-1, 3), crosses the y-axis at y = 2, passes through the point (1, 1), sharply changes direction at the point (2,0), goes linearly up and right, passes through the point (5, 2), and ends approximately at the point (7, 3.2).
Let u(x) = f(x)g(x) and
v(x) =
f(x)
g(x)
.
Answers
The output of each function include the following:
u'(1) = 0.
v'(5) = -2/3
How to determine the output of each function?By critically observing the graph of the functions f and g, we can logically deduce the following parameters;
f(1) = 2 f(5) = 3
g(1) = 1 g(5) = 2
f'(1) = 2 f'(5) = -1/3
g'(1) = -1 g'(5) = 2/3
Next, we would take the first derivative of u with respect to x and then, substitute the x-value into the composite function, and then evaluate as follows;
u(x) = f(x)g(x)
u'(x) = f'(x)g(x) + g'(x)f(x)
u'(1) = f'(1)g(1) + g'(1)f(1)
u'(1) = 2(1) + (-1)2
u'(1) = 2 - 2
u'(1) = 0.
For v'(5), we have the following function by applying quotient rule:
\(v'(x) = \frac{f'(x)g(x)\;-\;f(x)g'(x)}{g^2(x)} \\\\v'(5) = \frac{f'(5)g(5)\;-\;f(5)g'(5)}{g^2(5)} \\\\v'(5) = \frac{\frac{-1}{3} \times 2 - (3 \times \frac{2}{3}) }{2^2}\)
v'(5) = -8/3 × 1/4
v'(5) = -2/3
Read more on function here: https://brainly.com/question/31048166
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

one friday night, two large groups of people called wildgrove taxi service. the first group requested 1 sedan and 2 minivans, which can seat a total of 13 people. the second group asked for 3 sedans and 2 minivans, which can seat a total of 19 people. how many passengers can each type of taxi seat?
Answers
Each sedan can seat 2 passengers per type of taxi seat and each minivan can seat 2 passengers per type of taxi seat.
Total no. of sedans requested by the first group = 1
Total no. of minivans requested by the first group = 2
Total no. of people that can be seated = 13
Total no. of sedans requested by the second group = 3
Total no. of minivans requested by the second group = 2
Total no. of people that can be seated = 19
Now, the total no. of people for each type of taxi can seat = 13 passengers / 3 taxis.
By rounding up to the nearest value, 4 passengers per taxi.
No. of sedan seats = No. of passengers of a minivan.
By implementing division,
So, the total no. of passengers for each type of taxi can seat = 4/2 = 2 passengers.
Therefore, each sedan can seat 2 passengers per type of taxi and each minivan can seat 2 passengers per type of taxi.
To learn more about division:
https://brainly.com/question/28749372
#SPJ4
On average, Margo scores a goal for her field hockey team every 2 out of 3 shots. Margo uses a number cube to simulate her next three shots. She assigns 1 to 4 as goals and 5 and 6 as missed shots. Why does this assignment of numbers on the number cube make it a valid simulation?
Answers
Answer:
Margo makes 2/3 shots and making 4 shots and missing 2 shots equals 6 so 4/6 reduces to 2/3.
Step-by-step explanation:
4/6 = 2/3
find the unknown angle

Answers
Answer:
X&Y
Step-by-step explanation:
simple
very nice questions
Answer:
d: x equals 50 degrees and y equals 90 degrees
Step-by-step explanation:
thats the answer for the first one
A cone has a radius of 6 m and a height of 24 m. What is the volume of the cone in terms of π? 864π m3 432π m3 288π m3 144π m3
Answers
The volume of the cone in terms of π is 288π cubic meters, which corresponds to option (c) in the given answer choices.
The formula for the volume of a cone is:
V = (1/3)πr^2h
where V is the volume, r is the radius, and h is the height of the cone.
Plugging in the given values, we get:
V = (1/3)π(6 m)^2(24 m)
V = 288π m^3
Therefore, correct option is C.
This is because π is an irrational number that cannot be expressed as a finite decimal or fraction, so any approximation would be less precise than the exact value in terms of π.
To learn more about cone click on,
https://brainly.com/question/3302159
#SPJ4
help meeeeeeeeeeessss

Answers
Answer:
I think its c but just so you know I'm not really smart so I might be wrong
If you bought a stock last year for a price of $68, and it has gone down 6.5% since then how much is the stock worth now, to the nearest cent?
Answers
Answer:
Step-by-step explanation:
10.4615384615
PLEASE HELP (15 POINTS!!) PLEASE

Answers
Answer:
(4,9)
Step-by-step explanation:
To solve this, you can use substitution or elimination. In this case I would use substitution. To do this, you have to isolate a variable. x is already isolated so we can skip this step. plug x into 5x-7y=-43. This will make the equation 5(2y-14)-7y=-43. Simplify this to get 10y-70-7y=-43. Simplify this to get 3y-70=-43. Add 70 in both sides to isolate y. This will make the equation 3y=27. Divide both sides by 3 to make y equal to 1. This will make the equation y=9. Now you know that y=9. Plug 9 into any equation. x=2(9)-14. Simplify this to get x=18-14. x=4. Now put the numbers as an ordered pair which is (x,y). We know that x=4 and y=9 so it is (4,9).
If this answer has helped you please mark as brainliest.
Answer:
Where are you from ??
Step-by-step explanation:
From New Zealand ??
Use the following statements to write a compound
statement for the disjunction -p or -q. Then find its truth
value.
p: There are 14 inches in 1 foot.
q: There are 3 feet in 1 yard.
Answers
The disjunction of -p or -q can be written as (-p) v (-q). So, we have to find the truth value of (-p) v (-q). So, the compound statement for the disjunction of -p or -q is (-p) v (-q), and its truth value is true.
using the following statements: p: There are 14 inches in 1 foot.
q: There are 3 feet in 1 yard.
Solution: We know that 1 foot = 12 inches, which means that there are 14 inches in 1 foot can be written as 14 < 12. But this statement is false because 14 is not less than 12. Therefore, the negation of this statement is true, which gives us (-p) as true.
Now, we know that 1 yard = 3 feet, which means that there are 3 feet in 1 yard can be written as 3 > 1. This statement is true because 3 is greater than 1. Therefore, the negation of this statement is false, which gives us (-q) as false.
Now, we can use the values of (-p) and (-q) to find the truth value of (-p) v (-q) using the disjunction rule. The truth value of (-p) v (-q) is true if either (-p) or (-q) is true or both (-p) and (-q) are true. Since (-p) is true and (-q) is false, the disjunction of (-p) v (-q) is true. Hence, the compound statement for the disjunction of -p or -q is (-p) v (-q), and its truth value is true.
For more questions on: compound statement
https://brainly.com/question/28794655
#SPJ8
Sean is cutting construction paper into rectangles for a project. He needs to cut one rectangle that is 16 inches × 15 1/4 inches. He needs to cut another rectangle that is 10 1/2 inches by 10 1/4 inches. How many total square inches of construction paper does Sean need for his project?
Answers
Answer:
the total square inches of the construction paper is 351.63 square inches
Step-by-step explanation:
The computation of the total square inches of the construction paper is shown below;
= (16 × 15 1 ÷ 4) + (10 1 ÷2 × 10 1 ÷ 4)
= (16 × 61 ÷ 4) + (21 ÷ 2 × 41 ÷ 4)
= (16 × 15.25) + (10.5 × 10.25)
= 244 + 107.625
= 351.63 square inches
Hence, the total square inches of the construction paper is 351.63 square inches
We simply added these two
