how do you calculate the area and perimeter of a slope triangle?
Answers
Answer:
How you find the area of a triangle is by, multiplying two of the sides together then multiplying that by 1/2 or .5 . To find the perimeter of the triangle add all the three sides together!
Step-by-step explanation:
Related Questions
HELP ASAP!!
Which letter is the spinner least likely to land on?
The spinner is least likely to land on
Blank 1:

Answers
what is the probability that washing dishes tonight will take me between 15 and 16 minutes? give your answer accurate to two decimal places.
Answers
The probability of washing dishes by me tonight will take between 15 and 16 minutes is 14.29%.
The term "uniform distribution" refers to a type of probability distribution in which the likelihood of each potential result is equal.
Let's consider, the lower limit for this distribution as a and the upper limit for this distribution as b.
The following formula gives the likelihood that we will discover a value for X between c and d,
\(P(c\leq X\leq d)=\frac{d-c}{b-a}\)
Given the time it takes me to wash the dishes is 11 minutes and 18 minutes. From this, a = 11 and b = 18.
Then,
\(P(15\leq X\leq 16)=\frac{16-15}{18-11}=0.1429=14.29\%\)
The answer is 14.29%.
The complete question is -
The time it takes me to wash the dishes is uniformly distributed between 11 minutes and 18 minutes. What is the probability that washing dishes tonight will take me between 15 and 16 minutes?
To know more about uniform distribution:
https://brainly.com/question/17091893
#SPJ4
Enter the correct answer in the box.
Consider this expression.
x² + x - 72
Replace the values of a and b to rewrite the given expression.
(x+ a)(x+b)
Answers
(x + 9)(x - 8), where a = 9 and b = -8 or a = -8 and b = 9
The correct values of a and b to rewrite the expression as (x + a)(x + b) are:
a = 9
b = -8
So, (x + 9)(x - 8) is the correct form of the given expression.
Here, we have to rewrite the expression x² + x - 72 in the form (x + a)(x + b), we need to find two numbers a and b such that when multiplied,
it give us the constant term -72 and when added, it give us the coefficient of the x term, which is 1.
The expression x² + x - 72 can be factored as follows:
x² + x - 72
= x² + 9x - 8x - 72
=x(x+9) -8(x+9)
= (x + 9)(x - 8)
Therefore, the correct values of a and b to rewrite the expression as (x + a)(x + b) are:
a = 9
b = -8
So, (x + 9)(x - 8) is the correct form of the given expression.
To learn more on Expression click:
brainly.com/question/14083225
#SPJ7
PLEASE HELP ASAP
Apply the square root principle to solve (x-3)² + 9 = 0.
a. x=0,6
b. x=0,-6
c. x=-3+3i, -3 -3i
d. x=3+31,3-3i
Answers
The obtained value of x after solving the equation (x-3)² + 9 = 0 by the square root principle will be x=3+31,3-3i. Option d is correct.
What is the equation?An equation is a statement that two expressions, which include variables and/or numbers, are equal. In essence, equations are questions, and efforts to systematically find solutions to these questions have been the driving forces behind the creation of mathematics.
It is given that,
(x-3)² + 9 = 0
(x-3)²= -9
(x-3)=√-9
(x-3)=√9×√-1
(x-3)=±3i
x=3±3i
Thus, the obtained value of x after solving the equation (x-3)² + 9 = 0 by the square root principle will be x=3+31,3-3i. Option d is correct.
Learn more about the equation here,
https://brainly.com/question/10413253
#SPJ1
Convert the fraction below into a decimal: 7 3/4
Answers
Answer:
7.75
Step-by-step explanation:
7 is a whole so stays as such, 1/4 is 0.25 so 3/4 is 0.75
What is the value of x? Enter your answer in the box.
x =

Answers
Answer: 12
Step-by-step explanation:
A straight line has a measurement of 180° so these two angles added together will equal 180°.
(10x - 20)° + (6x + 8)° = 180°
10x° + 6x° + 8° - 20° = 180°
16x° -12° = 180°
16x° = 192°
x = 12
Supplementary angles
10x-20+6x+8=18016x-12=18016x=180+1216x=192x=192/16x=12a. Use any analytical method to find the first four nonzero terms of the Taylor series centered at 0 for the following function. You do not need to use the definition of the Taylor series coefficients
Answers
the first four nonzero terms of the Taylor series for the given function centered at 0 are 1, 5x, -2x^2, and x^3/3.
To find the Taylor series centered at 0 for a function, we can use the concept of derivatives evaluated at 0. The Taylor series expansion of a function f(x) centered at 0 is given by f(x) = f(0) + f'(0)x + (f''(0)x^2)/2! + (f'''(0)x^3)/3! + ...
For the given function, we need to compute the first four nonzero terms of its Taylor series centered at 0. Let's denote the function as f(x) = x^3 - 2x^2 + 5x + 1.First, we evaluate f(0) which is simply f(0) = 1.Next, we calculate the first derivative of f(x) and evaluate it at 0. The first derivative is f'(x) = 3x^2 - 4x + 5. Evaluating at 0, we get f'(0) = 5.Then, we find the second derivative f''(x) = 6x - 4 and evaluate it at 0, yielding f''(0) = -4.Finally, we compute the third derivative f'''(x) = 6 and evaluate it at 0, giving f'''(0) = 6.Now, we can substitute these values into the Taylor series expansion to obtain the first four nonzero terms:
f(x) = 1 + 5x - (4x^2)/2! + (6x^3)/3! + ...
Simplifying this expression, we have f(x) = 1 + 5x - 2x^2 + x^3/3 + ...
Learn more about Taylor series here:
https://brainly.com/question/32235538
#SPJ11
How do you find the scale factor of a dilation with a center of dilation?
Answers
The scale factor of dilation can be found by using the formula\((x_0=\frac{kx_1-x_2}{k-1}, y_0=\frac{ky_1-y_2}{k-1})\).
What is dilation?
A dilation is a transformation that creates an image that has the same shape as the original but is larger.
• An enlargement is a dilation that produces a larger image.
• A reduction is a dilation that produces a smaller image.
• A dilation expands or contracts the original figure.
A dilation is a stretch or a shrink in the size and location of a figure or point.
The scale factor in a dilation is the amount by which the figure is stretched or shrunk.
The center of dilation is a reference point used to appropriately scale the dilation of a figure. Given a point on the pre-image, \((x_1, y_1)\)and a corresponding point on the dilated image \((x_2, y_2)\)and the scale factor,
k, the location of the center of dilation, \((x_0,y_0)\) is
\((x_0=\frac{kx_1-x_2}{k-1}, y_0=\frac{ky_1-y_2}{k-1})\)
Hence, the scale factor of dilation can be found by using the formula\((x_0=\frac{kx_1-x_2}{k-1}, y_0=\frac{ky_1-y_2}{k-1})\).
To learn more about dilation, visit:
brainly.com/question/11914738
#SPJ4
Please help
What is the union of (a, e, i, o, u} and {q, r, s, t}?
Answers
Answer:
a, e, u, o, q, r, s, t, u is the union
6p- 2q for p = 3 and q = -7
Answers
Answer:
32
Step-by-step explanation:
plug in the values of the variables then simplify
Answer:
\(\boxed{32}\)
Step-by-step explanation:
Hey there!
Well given the expression,
6p - 2q
and p and q we need to plug them in.
6(3) - 2(-7)
Simplify
18 - -14
18 + 14
= 32
Hope this helps :)
Find the vertex of the graph of f(x)=-4(x-1)(x+5)
Answers
The vertex of the graph is (h, k) = (- 2, 36).
How to find analytically the vertex of a quadratic equation
In this question we have a quadratic equation of the form f(x) = a · (x - r₁) · (x - r₂) and we need to transform the expression into its vertex form of determine the coordinates of the vertex. First, we need to exprand the expression:
f(x) = - 4 · (x - 1) · (x + 5)
f(x) = - 4 · (x² + 4 · x - 5)
f(x) = - 4 · x² - 16 · x + 20
Now we proceed to complete the square:
f(x) = - (4 · x² + 16 · x - 20)
- f(x) = 4 · x² + 16 · x - 20
- f(x) = (2 · x)² + 8 · (2 · x) - 20
- f(x) + 36 = (2 · x)² + 8 · (2 · x) + 16
- f(x) + 36 = (2 · x + 4)²
- f(x) + 36 = 4 · (x + 2)²
f(x) - 36 = - 4 · (x + 2)²
The vertex of the graph is (h, k) = (- 2, 36).
To learn more on quadratic equations: https://brainly.com/question/17177510
#SPJ1
Victor must choose one pair of pants, one shirt, and one tie to wear to work. His possible choice combinations are shown in the tree diagram below.
If Victor chooses these work clothes at random, what is the probability that he will choose tan pants, a white shirt, and a red tie?
1/12
1/4
3/7
4/9

Answers
Answer:
should be 3/7 I think that's right
Graph the following equations by plotting 3 points and then connecting the points to form a line. Show your work to find the 3 points and then list the ordered pairs you used as part of your answer.


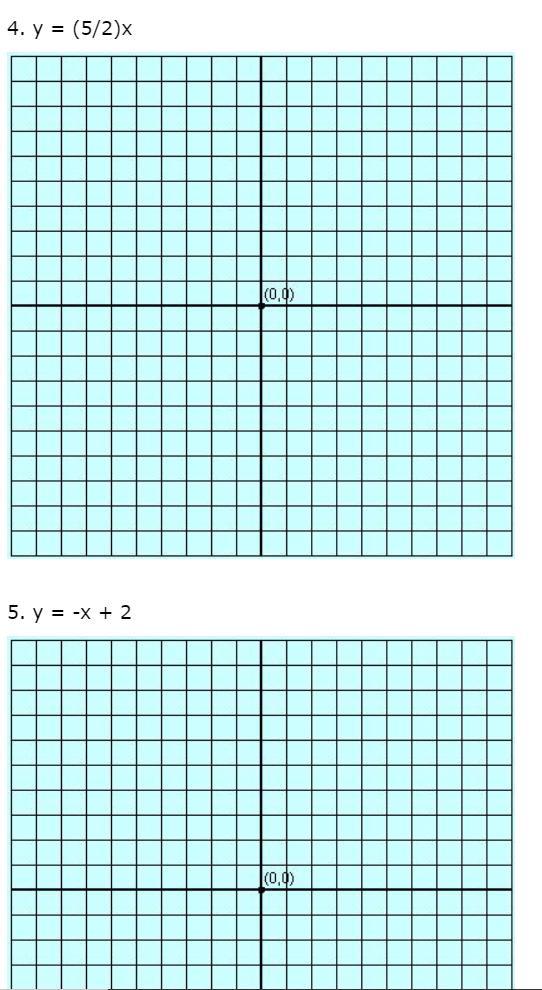


Answers
Answer:
The way I would tackle these types of problems would be to make a table, then graph the points using the results I get.
Step-by-step explanation:
So explaining the table is kinda hard since I suck at explaining, so I've attached a file showing the table I've made for number 1.
First Step:
Make the table. Make it a 3x4 table. For the top row, put y, the equation (I put 'y=2x' as shown in number 1), then x. Then for the left column, go down by one box, then put: -1, 0, 1. Really, you can put any numbers, but to make it easy for yourself, just write the numbers I've listed. These will be your y-values you'll be substituting.
Second Step:
a.) Plugging in the numbers. For the middle column, I've put down y=2x in each box, as shown in my table. Then for each of those boxes, plug in the numbers to the left of them and substitute them for the y-value. For example, look at the second row. The left box has '-1', so I replaced the 'y' in the equation and got '(-1)=2x'.
b.) After substituting the y-values, solve for x. For this case, you'll need to divide both sides by 2. If it doesn't make much sense, think about a seesaw. If you have 5 pounds on both sides, the seesaw will stay balanced. Add an additional 5 pounds to one side, then the seesaw will start tipping towards the heavier sides. So in order to keep an equation balanced, you must do any action to both sides of the equation. After diving both sides by 2, you'll get the value for x.
Final Step:
After finding the x-values for each of the y-values, it's time to graph the equations. Remember, x is left to right and y is down to up. To graph them, let's use the second row for example. y=-1 and x=-0.5. So all you need to do is to start from the origin (0,0), then go half a unit to the left, as x is negative, then go a unit down, as y is negative, then make a point. The rest should be pretty straight forward.
After making all three points, just get a ruler or any straight edge, then align it along those three points, then just make a line, and boom! You've solved number 1! For the purpose of saving my time, I'm pretty sure you can solve the rest using what I've just told you. Good luck!
Emily is 62 years old. Colin is 3 years older than Emily. Dan is 8 years younger than Emily. What is the total of their combined ages?
ASAP
thanks
example?
Answers
Dan’s age is 62-8=54 years old
The total is 65+54+62=181
Answer:
181
Step-by-step explanation:
Emily = 62
Collin = 3 years + Emily = 3 + 62 = 65
Dan = Emily - 8 years = 62 - 8 = 54
So, for finding the combined age,
=> 62 + 65 + 54
=> 181
If my answer helped, kindly mark me as the brainliest!!
Thank You!!
Quadrilateral ABCD is plotted on the grid below.121110987AB654321DС-12 -11 -10 9 8 76 5-4 3 2123-1 0-156789 10 11 12-2-56-78-9-10-11-12Part AOn the graph, draw the image of quadrilateral ABCD after a counterclockwise rotation of 180° about theorigin. Label the image A'B'C'D'.Part BOn the lines below, explain how the coordinates of A changed to the coordinates of A'.

Answers
The coordinates of the quadrilateral
A(5,6)
B(10,6)
C(8,1)
D(3,1)
Part A.
The rule for a rotation counterclockwise of 180°
\((x,y)\rightarrow(-x,-y)\)A'=(-5,-6)
B'=(-10,-6)
C'=(-8,-1)
D'=(-3,-1)
Then we will draw the quadrilateral
the original is the red
and the rotate is the blue
Part B
the coordinate change as the given rule seen previously for rotation of 180° counterclockwise
\((x,y)\rightarrow(-x,-y)\)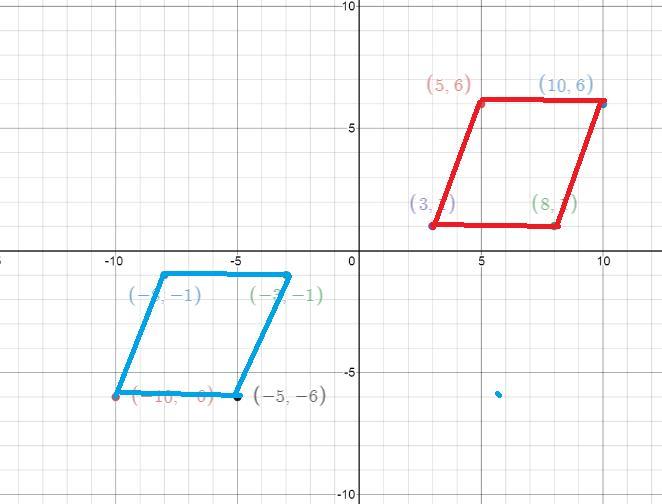
Two congruent ellipses are perpendicular to each other. Squares fill the gaps between the two ellipses as shown. Show that the side of the square equals half the minor axis of the ellipse.
Answers
The side of the square equals half the minor axis of the ellipse.
To show that the side of the square is half the minor axis of the ellipse, we must prove that the angles of the ellipses and the squares are congruent. To do this, we must first draw in the diagonals of the square, which will form two additional isosceles triangles.
Since the ellipses are perpendicular, the angles of the ellipses and the squares will be the same. Since the angles of the isosceles triangles are equal, the side of the square must be equal to half of the minor axis of the ellipse. Therefore, the side of the square is equal to half of the minor axis of the ellipse.
For more questions like Minor axis click the link below:
https://brainly.com/question/29054958
#SPJ4
during the two hours of the morning rush from 8 a.m. to 10 a.m., 100 customers per hour arrive at a coffee shop. this coffee shop has a capacity of 80 customers per hour. on average, how long does a customer arriving during the morning rush wait to be served?
Answers
Therefore, on average, a customer arriving during the morning rush would wait approximately 2.17 hours to be served.
To determine the average waiting time for a customer arriving during the morning rush at the coffee shop, we need to consider the arrival rate and the capacity of the shop.
Given that 100 customers per hour arrive at the coffee shop during the two-hour morning rush, and the shop has a capacity of 80 customers per hour, we can conclude that there will be more customers arriving than the shop can accommodate.
To calculate the average waiting time, we need to account for the time spent by customers who have to wait due to the shop being at full capacity. For simplicity, let's assume that customers arrive uniformly throughout the two-hour period.
During the first hour (8 a.m. to 9 a.m.), there will be 100 customers arriving, but the shop can only serve 80 customers. Therefore, 20 customers will have to wait for their turn to be served.
During the second hour (9 a.m. to 10 a.m.), again, 100 customers will arrive, but since the shop is already at full capacity, all 100 customers will have to wait for their turn.
In total, during the two-hour morning rush, there will be 20 customers who wait for one hour and 100 customers who wait for the entire two hours.
To calculate the average waiting time, we can sum up the waiting times and divide by the total number of customers:
Average waiting time = (20 * 1 hour + 100 * 2 hours) / (20 + 100) = (20 + 200) / 120 = 2.17 hours
To know more about morning rush,
https://brainly.com/question/22236958
#SPJ11
Which expression represents a number that is 4 times as great as the quotient of 25 and 5?
A. (25 x 5) x 4
B. 4 ÷ ( 25 ÷ 5 )
C. 4 x ( 25 ÷ 5 )
D. (25 ÷ 5 ) ÷ 4
Answers
Answer:
(25 ÷ 5 ) ÷ 4
Step-by-step explanation:
solve the equation for the variable. Then plug that variable value into the expression and simplify to get the answer.
Answer:
C
Step-by-step explanation:
the quotient of 25 and 5 is 25 ÷ 4 , then multiply this by 4 , so
4 × (25 ÷ 5 ) → C
The size (in millimeter) of a crack in a structural weld described by a random variable X with the following PDF: f_X(x) = {x/8 0 < x ≤2 1/4 2 < x ≤ 5 0 elsewhere. (a) Sketch the PDF and CDF on a piece of graph paper. (b) Determine the mean crack size. (c) What is the probability that a crack will be smaller than 4 mm?
Answers
The mean crack size is 1.25 mm.
How to calculate mean crack size?(a) To sketch the PDF and CDF, we can plot the given probability density function (PDF) on a graph paper.
The PDF f_X(x) is defined as follows:
f_X(x) = {
x/8 for 0 < x ≤ 2,
1/4 for 2 < x ≤ 5,
0 elsewhere
}
First, let's plot the PDF on the graph paper:
| . .
1/4 | . .
| . .
| . .
| . .
| . .
| . .
| . .
| . .
| . .
0.2 | . .
| . .
| . .
| . .
| . .
| . .
| . .
| . .
| . .
| . .
0.1 | . . . .
| . . . . . . . .
+----------------
0 2 4 6
The height of the PDF corresponds to the probability density at a given value of x.
Next, let's calculate the cumulative distribution function (CDF) to sketch it on the graph paper.
The CDF is obtained by integrating the PDF from negative infinity to x:
F_X(x) = ∫[0,x] f_X(t) dt
For 0 ≤ x ≤ 2:
F_X(x) = ∫[0,x] (t/8) dt = (1/8) * ∫[0,x] t dt = (1/8) * (t^2/2)|[0,x] = (1/8) * (x^2/2) = x^2/16
For 2 < x ≤ 5:The height of the PDF corresponds to the probability density at a given value of x.
Next, let's calculate the cumulative distribution function (CDF) to sketch it on the graph paper.
The CDF is obtained by integrating the PDF from negative infinity to x:
F_X(x) = ∫[0,x] f_X(t) dt
For 0 ≤ x ≤ 2:
F_X(x) = ∫[0,x] (t/8) dt = (1/8) * ∫[0,x] t dt = (1/8) * (t^2/2)|[0,x] = (1/8) * (x^2/2) = x^2/16
For 2 < x ≤ 5:The height of the PDF corresponds to the probability density at a given value of x.
Next, let's calculate the cumulative distribution function (CDF) to sketch it on the graph paper.
The CDF is obtained by integrating the PDF from negative infinity to x:
F_X(x) = ∫[0,x] f_X(t) dt
For 0 ≤ x ≤ 2:
F_X(x) = ∫[0,x] (t/8) dt = (1/8) * ∫[0,x] t dt = (1/8) * (t^2/2)|[0,x] = (1/8) * (x^2/2) = x^2/16
For 2 < x ≤ 5:F_X(x) = ∫[0,2] (t/8) dt + ∫[2,x] (1/4) dt = (1/8) * ∫[0,2] t dt + (1/4) * ∫[2,x] dt = (1/8) * (t^2/2)|[0,2] + (1/4) * (t)|[2,x] = (1/8) * 2 + (1/4) * (x-2) = 1/4 + (1/4) * (x-2) = 1/4 + (x-2)/4 = (x+1)/4
For x > 5:
F_X(x) = 1
Now, let's plot the CDF on the same graph paper:
| . . . . . . . .
1 | . . . . . . . .
| . . . . . . . .
| . . . . . . . .
| . . . . . . . .
0.8 | . . . . . . . .
| . . . . . . . .
| . . . . . . . .
| . . . . . . . .
0.6 | . . . . . . . .
| . . . . . . . .
| . . . . . . . .
| . . . . . . . .
0.4 | . . . . . . . .
|
Learn more about probability density
brainly.com/question/31039386
#SPJ11
Ramona is climbing a hill with a 10 incline and wants to know the height of the rock formation. She walks 100 ft up the hill and uses a clinometer to measure the angle of elevation to the top of the formation. What is the height h of the rock formation?

Answers
Answer:
40.4026226 aka 40.403
Step-by-step explanation:
tan 22 degrees = h/100
after how many years of follow-up would we expect the cumulative incidence of blindness to be 10% among 30-year-old iddm women, if the incidence rate remains constant over time? (round your answer to one decimal place.) years
Answers
After 13 years of follow-up would we expect the cumulative incidence of blindness to be 10% among 30-year-old iddm women, if the incidence rate remains constant over time.
In this question we have been given the annual incidence rate of blindness per year was 0.67% among 30- to 39-year-old male insulin-dependent diabetics (IDDM) and 0.74% among 30- to 39-year-old female insulin-dependent diabetics.
We need to find the number of years after which we expect the cumulative incidence of blindness to be 10% among 30-year-old IDDM females, if the incidence rate remains constant over time.
Let n be the number of years to expect the cumulative incidence of blindness to be 10% among 30-year-old IDDM females.
The probability of becoming blind over n years is 0.10
Given that the annual incidence rate of blindness per year was 0.74% IDDM females.
This means the rate r = 0.0074
For n years the annual incidence rate of blindness 0.0074n
We need to find the value of n,
0.0074n = 0.10
n = 13.51
n ≈ 13 years
Therefore, the number of years to expect the cumulative incidence of blindness to be 10% among 30-year-old IDDM females = 13
Learn more about the rate here:
https://brainly.com/question/199664
#SPJ4
The complete question is:
A study [12] of incidence rates of blindness among insulin-dependent diabetics reported that the annual incidence rate of blindness per year was 0.67% among 30- to 39-year-old male insulin-dependent diabetics (IDDM) and 0.74% among 30- to 39-year-old female insulin-dependent diabetics.
After how many years of follow-up would we expect the cumulative incidence of blindness to be 10% among 30-year-old IDDM females, if the incidence rate remains constant over time?
Someone help and explain please.

Answers
Answer:
k = 5/6
Step-by-step explanation:
The √ can be rewrite as a power, and this power is 1/2
So √a = a^1/2, and it is multiplying a, so we add the powers: a¹•a^1/2 = a^(1+1/2) = a^3/2
And the ³√ can be rewrite as the power 1/3, but the a inside the ³√ is to the power of 2, so we can rewrite it like this: (a²)^1/3
And to evaluate this we have to multiply the powers, so we will have: a^2/3
Now we have this fraction:
\( \frac{ {a}^{ \frac{3}{2} } }{ {a}^{ \frac{2}{3} } } \)
A fraction with powers in the same base can be rewrite like a subtraction of the powers, so let's do that:
\( \frac{ {a}^{ \frac{3}{2} } }{ {a}^{ \frac{2}{3} } } = {a}^{ \frac{3}{2} - \frac{2}{3} } = {a}^{ \frac{5}{6} } \)
Which of the following relations represent a function?
{(-1,-3),(3,2),(3,7)}
{(-1,4),(2,7),(3,7)}
{(-3,7),(3,-7),(3,7)}
{(-1,4),(-1,7),(3,5)}
Answers
You can only use the same value for x once
Answer: B is correct
Step-by-step explanation:
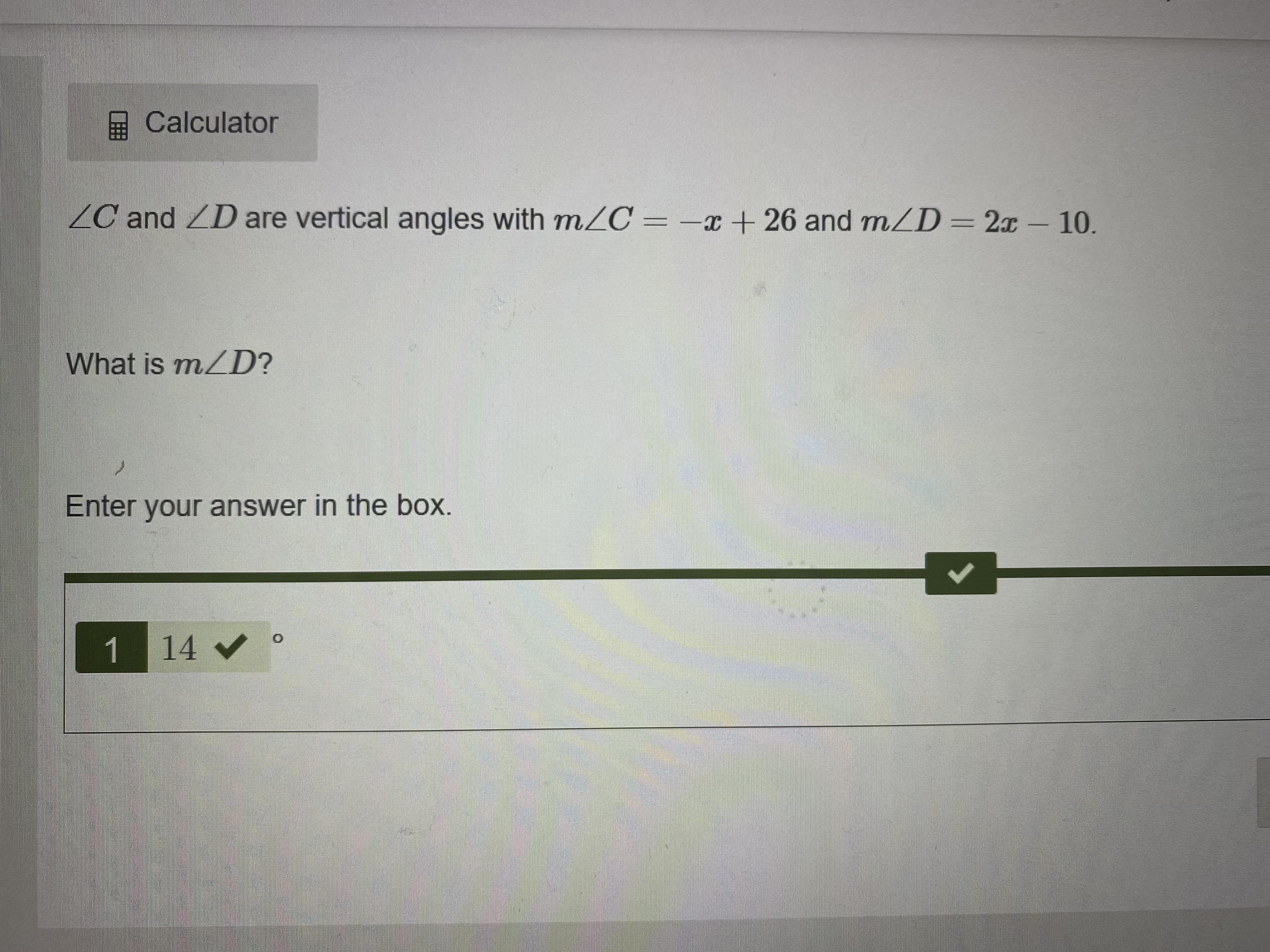
Angle C and angle D are vertical angles with m angle C = -x + 26 and m angle D = 2x - 10.
What is m angle D?

Answers
The answer is m<D=14*
−10. 74=u−(−11)minus, 10, point, 74, equals, u, minus, left parenthesis, minus, 11, right parenthesis
Answers
The given equation [−10. 74=u−(−11)] yields the value of u as "-21.74".
The equation is [−10. 74=u−(−11)]
In order to solve this equation simple mathematical operations are perfromed. Steps by step solution is given here:
[−10. 74=u−(−11)]
[-10.74 = u + 11]
To determine the value of u, it is required to take constants to one side the equation, so
[-10.74 - 11 = u]
[-21.74 = u]
The value of u is -21.74.
So after solving the given equation which is [−10. 74=u−(−11)] , the value of u to be determined is "-21.74."
You can learn more about equation at
https://brainly.com/question/25976025
#SPJ4
Ainsley works for the owners of a bookstore. Her starting salary was 24,500, and she gets a 3% raise each year. Write an equation in function notation to represent subsidy’s salary as a function of the number of years she has been working at the bookstore. What will Ainselys salary be when she begins her fourth year working at bookstore?
Answers
Answer:
if x is the number of years she is working that the equation would be: 24,500+x*((3/100)*24,500)
Step-by-step explanation:
For her 4th year x would be 4, so for the equation above x=4:
24500+4*((3/100)*24500)=27440
White Water season pass cost $52 with a one time fee of $16. A six flags season pass is $60per person. How many people will it take for the white water pass and the six flags season pass to cost the same
Answers
Explanation: Since we want the two passes to cost the same, we can set them equal to each other.
Thus, we have 52p+16=60p
Solving for p gives us 2. 60*2=120; 52(2)+16=120
Can you answer this question for me Thank you For the school cafeteria, 15 pounds of vegetables were ordered by the chef. If each student usually gets 3/8 of a pound of vegetables each day for lunch, how many students could be fed with the vegetables in one day?
Answers
Answer:
The answer could be 40. I might be wrong.
Step-by-step explanation:
15 divided by 3/8 = 40
Help with both questions please

Answers
First one is -1. The second one is 1/2.
1: -1
2: 1/2
2) A 4-digit number will be formed using the digits 1, 2, 3, 4, 5, 6, 7,9. Each digit will only be used once, if at all. Note that there is no 8. a) How many possible 4-digit numbers are possible? TOTAL: b) Assume four of the digits are randomly chosen and randomly permuted in order to form the 4-digit number. Then each of the possible 4-digit numbers in part a) are equally likely. Find the probability that the 4-digit number ends up being an odd number greater than or equal to 6000? Hint: Partition the event that the number is odd and greater than or equal to 6000 into: • the event that the number is odd and between 6000 & 6999 inclusive • the event that the number is odd and greater than or equal to 7000. (odd numbers in [6000,6999 ways (odd numbers 7000 or more) ways PROBABILTY:
Answers
The possible 4-digit numbers are 1,680.
Probability that 4-digit number ends up being an odd number greater than or equal to 6000 is 57.14%.
How to calculate probability?a) The number of possible 4-digit numbers that can be formed using the given digits without repetition is given by the permutation formula:
P(8,4) = 8! / (8 - 4)! = 8 x 7 x 6 x 5 = 1,680
Therefore, there are 1,680 possible 4-digit numbers using the given digits.
b) The total number of 4-digit numbers that can be formed from the given digits is 1,680, as calculated in part a).
To find the probability that the 4-digit number is odd and greater than or equal to 6000, we need to calculate the number of odd 4-digit numbers in the range [6000, 6999] and the number of odd 4-digit numbers greater than or equal to 7000, and divide each by the total number of 4-digit numbers.
Number of odd 4-digit numbers in [6000, 6999]:
The last digit must be 1, 3, 5, or 7 (4 choices). The first three digits can be any of the remaining 7 digits (7 choices for the first digit, 6 choices for the second digit, and 5 choices for the third digit). Therefore, the number of odd 4-digit numbers in [6000, 6999] is:
4 x 7 x 6 x 5 = 840
Number of odd 4-digit numbers greater than or equal to 7000:
The first digit must be 7 (1 choice). The last digit must be 1, 3, 5, or 7 (4 choices). The second and third digits can be any of the remaining 6 digits (6 choices for the second digit and 5 choices for the third digit). Therefore, the number of odd 4-digit numbers greater than or equal to 7000 is:
1 x 4 x 6 x 5 = 120
The total number of odd 4-digit numbers is 840 + 120 = 960.
Therefore, the probability that the 4-digit number is odd and greater than or equal to 6000 is: 960 / 1,680 = 0.5714 or approximately 57.14%.
Learn more on probability here: https://brainly.com/question/24756209
#SPJ1