How does the average change if the minimum number is
removed from the list below? Round your answer to the nearest hundreths.
24 36 10 56 12 6 41 28
A
Increase by 2.95
B
Decrease by 2.95
Increase by 0.75
D Decrease by 0.75
E
Decrease by 3.12
Answers
9514 1404 393
Answer:
A Increase by 2.95
Step-by-step explanation:
Suppose the current average is A. Then the sum of the 8 items being averaged is 8A. We observe the minimum of those items is 6, so removing that from the sum gives 8A-6. The new average of the 7 remaining items is ...
A' = (8A -6)/7
The difference between the new average and the old one is ...
A' -A = (8A -6)/7 -A = (A -6)/7
The average of the given items is ...
(24 +36 +10 +56 +12 +6 +41 +28)/8 = 26.625
so the change in the average will be ...
(26.625 -6)/7 ≈ 2.9464 ≈ 2.95 . . . an increase
The removal of the minimum number from the average will increase it by about 2.95.
_____
Additional comment
The average is always greater than the minimum item, so removing the minimum item from the list will always increase the average. The amount of increase depends on the relationship between the average and the minimum, as we calculated above.
Related Questions
Find a point on the line and the line's slope. y - 1 = -4/3 (x -4)
point on line:
slope:
Answers
Answer:
\(\displaystyle\text{Slope: } -\frac{4}{3}\)
Point (4,1)
Step-by-step explanation:
The Equation of the Line
The point-slope form of the equation of a line is:
y - k = m ( x - h )
Where m is the slope and (h,k) is a point through which the line passes.
The given line is:
\(\displaystyle y-1=-\frac{4}{3}(x-4)\)
If we compare the equation of this line, both the slope and the point through which is passes are clearly identifiable:
Slope:
\(\mathbf{\displaystyle -\frac{4}{3}}\)
Point (4,1)
area of triangle۔ab =154،bc=346،ac=349
Answers
Therefore, the area of the triangle ABC is approximately 18096.3 square units.
What is the area of the triangle?
To calculate the area of a triangle, use the formula area = 1/2 * base * height.
We can use Heron's formula to find the area of the triangle ABC when the lengths of its three sides are known:
\(Area = {\sqrt{(s(s-a)(s-b)(s-c))}\)
where "s" is the semiperimeter of the triangle, which is half the sum of the lengths of its three sides:
s = (a + b + c)/2
In this case, we have:
a = AB = 154
b = BC = 346
c = AC = 349
So the semiperimeter is:
s = (a + b + c)/2 = (154 + 346 + 349)/2 = 424.5
Now we can use Heron's formula to find the area of the triangle
\(Area = \sqrt{(s(s-a)(s-b)(s-c))}\\\\Area = \sqrt{(424.5(424.5-154)(424.5-346)(424.5-349))}\\\\Area= 18096.3\)
Therefore, the area of the triangle ABC is approximately 18096.3 square units.
To know more about area of the triangle visit,
https://brainly.com/question/17335144
#SPJ1
A rock climber is planning to climb a mountain cliff over two days. The climb begins at an altitude of 6,400 feet above sea level. The rock climber figures
he can climb at an average pace of 360 feet per hour. He wants to climb to an altitude higher than 8,020 feet above sea level by the end of the first day of
climbing.
Which inequality and solution describe how many hours the climber must climb on the first day to reach his goal?
A
360h + 6,400 < 8,020, with a solution of h < 4
2
B
360h + 6,400 < 8,020, with a solution of h < 7
71
C
360h + 6,400 > 8,020, with a solution of h > 75
18
D
360h + 6,400 > 8,020, with a solution of h > 4.
2

Answers
Answer:
D
Step-by-step explanation:
360h+6,400 >8,020, with a solution is h> 4.
An account with a $250 balance accrues 2% annually.
Answers
A car travels a distance of 112km at an average Speed of 70km/h. It then Travells Further for 60km at an average Speed of 50 km/hr. Calculate for the entire Journey of the total time taken.
Answers
The total time taken for the entire journey is 2.8 hours.
To calculate the total time taken for the entire journey, we can use the formula:
Time = Distance / Speed
For the first part of the journey, the car travels a distance of 112 km at an average speed of 70 km/h. Using the formula, the time taken for this part is:
Time1 = 112 km / 70 km/h = 1.6 hours
For the second part of the journey, the car travels a further distance of 60 km at an average speed of 50 km/h. Again, using the formula, the time taken for this part is:
Time2 = 60 km / 50 km/h = 1.2 hours
To find the total time for the entire journey, we sum up the times for both parts:
Total Time = Time1 + Time2 = 1.6 hours + 1.2 hours = 2.8 hours
For more such questions on time
https://brainly.com/question/26862717
#SPJ8
after 6 hours of burning, it has a height of 25.2 centimeters. after 24 hours of burning , its height is 19.8 centimeters, what is the height of the candle after 19 hours
need answers quickly please
Answers
Answer:
21.3 cm
Step-by-step explanation:
first find the rate of change (RISE/RUN)
\(\frac{19.8-25.2}{24-6}\) which gives you -0.3
Next, create an equation. You can choose any point, but I chose (6,25.2) because it is given.
y - 25.2 = -0.3(x-6)
y - 25.2 = -0.3x + 1.8
y = -0.3x + 27
Finally, plug in 19 for x...
y = -0.3(19) + 27 = 21.3 cm
Workers at a quarry are removing rock at a daily rate of 0.1%. There are 3.2 tons of rock when the work begins.
Which function can be used to find the number of tons of rock left at the end of d days?

Answers
Answer:
c
Step-by-step explanation:
H
6:00 PM
What is a frostbite?
Answers
Are the triangles below right, obtuse or acute?

Answers
The figure shows four box-and-whisker plots. These represent variation in travel time for four different types of transportation from the beginning to the end of one route.
Conrad is at one end of the route. He is trying to decide how to get to an appointment at the other end. His appointment is in 30 minutes. Which type of transportation is LEAST likely to take more than 30 minutes?
Select one:
a.
bus
b.
car
c.
subway
d.
train

Answers
Comparing the median of each box-and-whisker plot, the type of transportation that is LEAST likely to take more than 30 minutes is: d. train.
How to Interpret a Box-and-whisker Plot?
In order to determine the transportation that is LEAST likely to take more than 30 minutes, we have to compare the median of each data set represented on the box-and-whisker plot for each transportation.
The box-and-whisker plot that has the lowest median would definitely represent the the transportation that is LEAST likely to take more than 30 minutes, since median represents the typical minutes or center of the data.
Therefore, from the box-and-whisker plots given, the one for train has the lowest median. Therefore train would LEAST likely take more than 30 minutes.
Learn more about box-and-whisker plots on:
brainly.com/question/27849170
#SPJ1
Right triangle LMN has vertices L(7, –3), M(7, –8), and
N(10, –8). The triangle is translated on the coordinate plane so the coordinates of L’ are (–1, 8).
Answers
In this case we have a translation of 8 units to the left and 11 units upwards.
How to find the translation?To find the translation, we just need to compare the two known vertices before and after the translation.
If we have a translation of a units in the x-axis and b units in the y-axis, we will get:
T(a, b)L ---> L'
We know that L = (7, -3) and L' = (-1, 8)
Then we can write:
(7 + a, -3 + b) = (-1, 8)
Then we have two equations:
7 + a = -1 ---> a = -1 - 7 = -8
-3 + b = 8 ---> b = 8 + 3 = 11
Then we have a translation of 8 units to the left and 11 units up-.
Learn more about translations at:
https://brainly.com/question/1046778
#SPJ1
Complete question:
"Right triangle LMN has vertices L(7, –3), M(7, –8), and
N(10, –8). The triangle is translated on the coordinate plane so the coordinates of L’ are (–1, 8).
Find the translation done"
A function is defined by f(x)=x/4 What is f(-8)
Answers
Answer:
f(-8) = -2
Step-by-step explanation:
f(x)=x/4
Let x = -8
f(-8)=-8/4
f(-8) = -2
The distance from the tip of a slice of pizza to the crust is 7 inches.
Does this represent diameter, circumference, or radius?
ANSWER ASAP THANK YOU
Answers
Answer:
radius
Step-by-step explanation:
square with a perimeter of 240 inches is dilated by a scale factor of 1.5. what is the area of the dilated image of the square?
Answers
the awnser: is 960 inches
Margo brought 7 pens from a book store some pens cost $3.00 EACH and the rest cost $4.00 . If she paid a total of 23.00 for the pens how many of the $3.00 pens did she buy
Answers
Answer:
5
Step-by-step explanation:
Margo bought 7 pens for $23.
Some pens are $3 and some $4.
We need to find how many $3 pens she bought.
Let the number of $3 pens be represented by p and let the number of $3 pens be represented by r. So:
p = $3 and r = $4
Now we know 7 pens were purchased so is we add the number of $3 pens purchased to the number of $4 pens purchased, we will get 7.
p + r = 7
We know that the total cost of the pens is $23 so that equation would be found by takign the $3 pen multiplied by the number of $3 pens purchsed added to the $4 pen multiplied by the number of $4 pens purchsed, which equals $23.
$3p + $4r = $23
Now we have 2 equations and 2 unknowns.
p + r = 7
$3p + $4r = $23
Let's solve for r in the first equation.
p + r = 7 Subtract p from both sides.
p - p + r = 7 - p The p on the left cancels.
r = 7 - p
Now that we know r, we can substitute it into the second equation and solve for p.
$3p + $4r = $23
3p + 4( 7 - p) = 23 Multiply it out.
3p + 4*7 - 4*p = $23
3p + 28 - 4p = 23 Combine like terms.
3p - 4p + 28 = 23
- 1p + 28 = 23 Subtract 28 from both sides.
- p + 28 - 28 = 23 - 28
- p = - 5 Divide each side by -1
- p/- 1 = - 5/ - 1 The negative cancels on each side.
p = 5
We can see Margo bought 5 $3 pens.
For fun, let's solve for how many $4 pens she bought. We know p, so we plug it in the first equation and solve for r.
p + r = 7
5 + r = 7 Subtract 5 from each side
5 - 5 + r = 7 - 5
r = 7 - 5
r = 2
So Margo bought 5 $3 pens and 2 $4 pens!
5
Enter the correct answer in the box.
Solve the quadratic equation by completing the square.
2x² + 12x = 66
Fill in the values of a and b to complete the solutions.
x=a-√b
x=a+√b
Answers
The values of a and b are a = -3 and b = 42. The solutions for x can be written as:
x = -3 - √42
x = -3 + √42
To solve the quadratic equation 2x² + 12x = 66 by completing the square, we need to follow these steps:
Step 1: Move the constant term to the right side:
2x² + 12x - 66 = 0
Step 2: Divide the equation by the leading coefficient (2):
x² + 6x - 33 = 0
Step 3: To complete the square, we take half of the coefficient of x, square it, and add it to both sides of the equation:
x² + 6x + (6/2)² = 33 + (6/2)²
x² + 6x + 9 = 33 + 9
x² + 6x + 9 = 42
Step 4: Rewrite the left side as a perfect square:
(x + 3)² = 42
Step 5: Take the square root of both sides:
√(x + 3)² = ±√42
x + 3 = ±√42
Step 6: Solve for x:
x = -3 ± √42.
For such more questions on Solutions:
https://brainly.com/question/24644930
#SPJ11
Triangle in space with vertices P= (1, 0, 0), Q = (0,1,0), R=(0, 0, 2), find angle at P P=
Answers
Answer:
71.6°
Step-by-step explanation:
The angle can be found from the dot product of PQ and PR.
PQ·PR = |PQ|×|PR|×cos(α)
where α is the angle between the two segments.
cos(α) = (Q -P)·(R -P)/(|Q -P|×|R -P|)
= ((0, 1, 0) -(1, 0, 0))·((0, 0, 2) -(1, 0, 0))/(|Q -P|×|R -P|)
= (-1, 1, 0)·(-1, 0, 2)/(√(((-1)² +1²)((-1²) +2²)) = (1+0+0)/√10
α = arccos(1/√10) ≈ 71.6°
The angle at P is about 71.6°.
_____
Additional comment
The side lengths of the triangle are √2, √5, √5. As we have seen, the angle at P is bounded by the sides of length √2 and √5. The law of cosines can also be used to arrive at the angle between these sides.
There are 6 fiction books and 8 nonfiction books on a reading list. Your teacher randomly assigns you 4 books to read over summer. What is the probability that you are assigned all nonfiction books?
Answers
Answer:
Step-by-step explanation:

help im bad at math AHHHHHHHHHHHHHHHHHHHHH

Answers
Answer:
36
Step-by-step explanation:
Answer:
The answer is D
Step-by-step explanation:
because am very good at math
Find the surface area of a cylinder with a height of 8 and a base radius of 5 m.
Use the value 3.14 for, and do not do any rounding.
Be sure to include the correct unit.

Answers
Using the height and radius given, the surface area of the cylinder is 408.2m²
What is surface area of a cylinder?The surface area of a cylinder is the combined area of its curved surface (lateral surface) and its two circular bases. The formula for the surface area of a cylinder is:
A = 2πrh + 2πr²
where:
A is the surface area of the cylinder,π is the mathematical constant r is the radius of the base of the cylinder, andh is the height (or length) of the cylinder.In the given question, the data are;
h = 8mr = 5mSubstituting the value into the formula
A = 2π(5 * 8) + 2π(5)²
A = 408.2m²
Learn more on surface area of cylinder here;
https://brainly.com/question/27440983
#SPJ1
Which is the correct value of Z for the solution to true system?
2x+3y-z=4
x-3y+2z=-3
3x+y-z=5

Answers
The correct value of Z for the solution to true system is -2
How to determine the correct value of Z for the solution to true system?From the question, we have the following parameters that can be used in our computation:
2x + 3y - z = 4
x - 3y + 2z = -3
3x + y - z = 5
Transform the third equation
So we have
2x + 3y - z = 4
x - 3y + 2z = -3
9x + 3y - 3z = 15
Eliminate y in the equations by subtraction
So we have
x - 3z = 7
10x - z = 12
Multiply x - 3z = 7 by 10
10x - 30z = 70
10x - z = 12
Subtract the equations
-29z = 58
So, we have
z = -2
Hence, the correct value of Z is -2
Read more about equations at
https://brainly.com/question/148035
#SPJ1
I think i need assistance
please help
and if you do i will give u a brain list thing
5 mins left

Answers
Answer:
4(2x - 1) + 3(2x + 5)
Step-by-step explanation:
4(2x - 1) + 3(2x+5)
Multiply 4 with 2x - 1 and multiply 3 with 2x + 5,
8x - 8 + 6x + 15 = 0
Arrange x and constant,
8x + 6x = 8 - 15
14x = - 7
14x = - 7
x = -7/14
x = -1/2
x = -0.5
Hope this helps! Recheck the answers.
number 5 find the general solution to the differentiabel equation

Answers
To solve the differential equation, proceed as follows:
\(\begin{gathered} \frac{dy}{dx}=2y-1 \\ \frac{1}{2y-1}dy=1dx \end{gathered}\)Integrate each side of the equation:
\(\begin{gathered} \int \frac{1}{2y-1}dy=\int 1dx \\ \frac{1}{2}\ln |2y-1|=x+C \end{gathered}\)Solve for y:
\(\begin{gathered} \ln |2y-1|=2x+C \\ e^{\ln |2y-1|}=e^{2x+C} \\ 2y-1=e^{2x}e^C \\ 2y=Ce^{2x}+1 \\ y=\frac{Ce^{2x}+1}{2} \end{gathered}\)Substitution method:
\(\begin{gathered} \int \frac{1}{2y-1}dy \\ u=2y-1 \\ du=2dy \\ dy=\frac{du}{2} \\ \int \frac{1}{2u}du \\ \frac{1}{2}\int \frac{1}{u}du \\ \frac{1}{2}\ln |u| \\ \frac{1}{2}\ln |2y-1| \end{gathered}\)A telephone company charges $30 a month and gives the customer 200 free minutes. After the 200 min, the company charges $0.03 a minute.
(a) Write the function using function notation.
(b) Find the cost for talking 350 min in a month
(c) Find the number of minutes used if the monthly charge is $34.68
Answers
Answer:
(a)
f(x) = 30, for x ≤ 200
f(x) = 0.03(x - 200) + 30, for x > 200
(b) $34.50
(c) 356
Step-by-step explanation:
Let x = number of minutes.
(a)
f(x) = 30, for x ≤ 200
f(x) = 0.03(x - 200) + 30, for x > 200
(b)
Here, x = 350, so x > 200.
f(x) = 0.03(x - 200) + 30
f(350) = 0.03(350 - 200) + 30
f(350) = 0.03(150) + 30
f(350) = 4.5 + 30
f(350) = 34.5
$34.50
(c)
f(x) = 0.03(x - 200) + 30
0.03(x - 200) + 30 = 34.68
0.03(x - 200) = 4.68
x - 200 = 156
x = 356
Marsha pays $25 each month for a car wash membership. Which of the following represents the total amount subtracted from her account after 4 months of having the membership?
A. −4|25| = −$100
B. 4|−25| = $100
C. |−25| − |4| = $21
D. |−25| − 4 = $21
Answers
Answer:
B. 4|−25| = $100
Step-by-step explanation:
Hope this helps!
Which of the following is not a polynomial? HELP QUICK

Answers
Use Polya's four-step problem-solving strategy and the problem-solving procedures presented in this lesson to solve the following exercise.
Find the following sums without using a calculator or a formula. Hint: Apply the procedure used by Gauss. (See the Math Matters on page 31.)
+393 +394 + 395
(a) 1+2+3+4+...+392
(b) 1+2+3+4
x
546 + 547 +548 + 549
(c) 2+4+6+8+...+76 + 78 + 80 +82
Answers
(a) The sum of the series 1+2+3+4+...+392 is 77,028.
(b) The sum of the series 1+2+3+4...x is (x/2)(1 + x).
(c) The sum of the series 546 + 547 + 548 + 549 is 2,190.
To solve the exercise using Polya's four-step problem-solving strategy, we will apply the procedures presented in the lesson.
(a) For the series 1+2+3+4+...+392:
Using the arithmetic series formula Sn = (n/2)(a + l), where n is the number of terms, a is the first term, and l is the last term, we can substitute the values: Sn = (392/2)(1 + 392) = 196(393) = 77,028.
(b) For the series 1+2+3+4...x:
To find the sum of this series, we need to know the number of terms (n) based on the value of x. Since the series follows a consecutive pattern, the number of terms will be equal to x itself. Thus, the sum of the series would be Sn = (x/2)(1 + x).
(c) For the series 546 + 547 + 548 + 549:
Using the arithmetic series formula Sn = (n/2)(a + l), we can determine the number of terms (n) by subtracting 546 from 549 and then adding 1: n = 549 - 546 + 1 = 4. Substituting the values into the formula: Sn = (4/2)(546 + 549) = 2(1095) = 2,190.
The final answer for each part is:
(a) The sum of the series 1+2+3+4+...+392 is 77,028.
(b) The sum of the series 1+2+3+4...x is (x/2)(1 + x).
(c) The sum of the series 546 + 547 + 548 + 549 is 2,190.
for such more question on series
https://brainly.com/question/29062598
#SPJ8
The coordinates of the point that is a reflection of Y(-4, -2) across the x-axis are ( , ). The coordinates of the point that is a reflection of Y across the y-axis are ( , ).
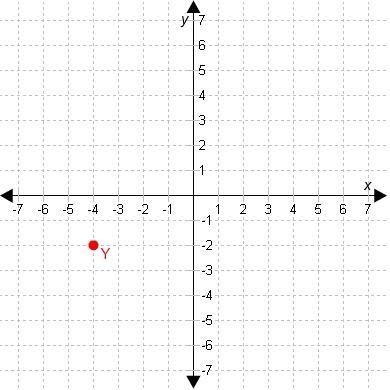
Answers
Answer:
Reflection across the x-axis: (-4,2)
Reflection across the y-axis: (4,-2)
Step-by-step explanation:
Going based off of what I see, a reflection across the x axis changes "y" & the same rule applies to the y axis.
It should be an L shape.
If f (p) = 7p³ - 5p² + 1/3p what is f(3)

Answers
Answer: f(3) = 145 ==> 1st option
Step-by-step explanation:
f(p) = 7p³ - 5p² + 1/3p
f(p) = 7p³ - 5p² + p/3
f(3) = 7(3)³ - 5(3)² + (3)/3
f(3) = 7(27) - 5(9) + 1
f(3) = 189 - 45 + 1
f(3) = 144 + 1
f(3) = 145 ==> 1st option
Find the value of x in the equation 13 - X =21
Answers
Answer:
x=-9
Step-by-step explanation:
\(13-x=21\\\\12-x+x=21+x\\\\12+0=21+x\\\\21+x=12\\\\21-21+x=12-21\\\\0+x=-9\\\\x=-9\)
Answer:
- 8
Step-by-step explanation:
13 - x = 21
-x = 8 Subtract 13 from both sides
x = -8 Divide both sides of -1 since x still has a negative.