How many permutations of S9, have cycle strucrure 3^3?
Answers
There is only 1 permutation in S9 with a cycle structure of \(3^3\).
To find the number of permutations of S9 with a cycle structure of \(3^3\), we can use the concept of cycle index.
In a permutation with a cycle structure of\(3^3\), we have three cycles of length 3. The cycle index of S9 with respect to cycles of length 3 can be determined using the Polya enumeration theorem.
The cycle index of S9 with respect to cycles of length 3 is given by:
\(Z(S9, t1, t2, t3) = (t1^3 + t3^3)^3\)
Expanding this expression, we get:
\(Z(S9, t1, t2, t3) = (t1^3 + t3^3)^3\\\= (t1^9 + 3t1^6t3^3 + 3t1^3t3^6 + t3^9)\)
To count the number of permutations with the desired cycle structure, we need to find the coefficient of the term \(t1^9t3^9\).
From the expanded form, we see that the coefficient \(t1^9t3^9\) is 1.
Therefore, there is only one permutation in S9 with a cycle structure of \(3^3\)
In summary, there is 1 permutation of S9 that has a cycle structure of \(3^3\).
Read more about Permutation at;
brainly.com/question/12468032
#SPJ4
Related Questions
PLEASE HELP AND EXPLAIN HOW YOU GOT THE ANSWER. I WILL MARK YOU BRAINLIEST
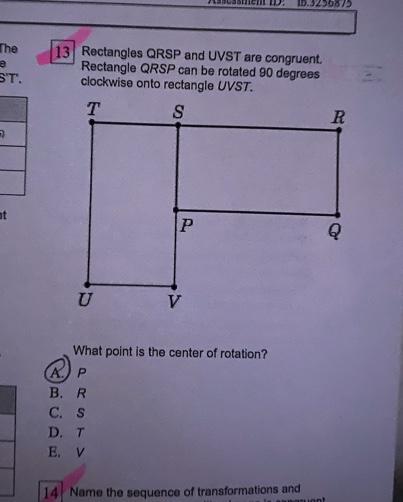
Answers
Answer:
The point that is the center of rotation is S!
Take this second rectangle, the one on the right, and see where the two rectangles share a point? (QRSP and UVST both share an S). Imagine you’re putting a pin in it- this point should not move. Now rotate R, Q, and P down and to the right- clockwise! After a 90° rotation, all four corners will meet. Does that make sense? I can find a different way to explain if needed!
Solve the quadratic for x. Select all that apply.
x? + 7x - 30 = 0
O A. X=3
O B. X=-6
C. X=-10
D. X=-3
O E.X=5
O F.x=6

Answers
Hope this helps
Help please I need to catch up on work

Answers
Answer:
Step-by-step explanation:
y = -6x + 3
When x = -5 ; y = -6*(-5) + 3 = 30 + 3 = 33
When x = -1 ; y = -6*(-1) +3 = 6 + 3 = 9
When x = 0 ; y = 0+3 = 3
When x = 1 ; y = -6 *1 + 3 = - 6 + 3 = - 3
Answer:
1.33
2.9
3.3
4.-3
Step-by-step explanation:
hope u caught up with your work
Find the general solution of the following equations by integrating. N.B. Please use A for the first constant of integration, B for the second and C for the third.
(a) y′=4t3+t
Solution: y=
(b) y′′=4t3+t Solution:
y=
(c) d3xdt3=4t3+t
Solution: x=
(d) 2y′=3t+2 Solution:
y=
Answers
a) The general solution is y = t^4/4 + t^2/2 + A, b) The general solution is y = t^5/20 + t^3/6 + At + B, c) the general solution is x = t^6/120 + t^4/24 + At^2/2 + Bt + C d) The general solution is y = 3t^2/4 + t + A/2
(a) To find the general solution of y′=4t^3+t, we need to integrate both sides of the equation with respect to t. This gives us:
y = ∫(4t^3+t)dt = t^4/4 + t^2/2 + A
So the general solution is y = t^4/4 + t^2/2 + A, where A is the first constant of integration.
(b) To find the general solution of y′′=4t^3+t, we need to integrate both sides of the equation twice with respect to t. This gives us:
y′ = ∫(4t^3+t)dt = t^4/4 + t^2/2 + A
y = ∫(t^4/4 + t^2/2 + A)dt = t^5/20 + t^3/6 + At + B
So the general solution is y = t^5/20 + t^3/6 + At + B, where A is the first constant of integration and B is the second constant of integration.
(c) To find the general solution of d^3x/dt^3=4t^3+t, we need to integrate both sides of the equation three times with respect to t. This gives us:
d^2x/dt^2 = ∫(4t^3+t)dt = t^4/4 + t^2/2 + A
dx/dt = ∫(t^4/4 + t^2/2 + A)dt = t^5/20 + t^3/6 + At + B
x = ∫(t^5/20 + t^3/6 + At + B)dt = t^6/120 + t^4/24 + At^2/2 + Bt + C
So the general solution is x = t^6/120 + t^4/24 + At^2/2 + Bt + C, where A is the first constant of integration, B is the second constant of integration, and C is the third constant of integration.
(d) To find the general solution of 2y′=3t+2, we need to integrate both sides of the equation with respect to t. This gives us:
2y = ∫(3t+2)dt = 3t^2/2 + 2t + A
y = (3t^2/2 + 2t + A)/2 = 3t^2/4 + t + A/2
So the general solution is y = 3t^2/4 + t + A/2, where A is the first constant of integration.
Learn more about the general solutions:https://brainly.com/question/30465681
#SPJ11
A backpack that normally sells for $39 is on sale for $25. Find the
percent of change.
Answers
Answer: To find the discount, simply multiply the original selling price by the %discount:
ie: 39 x 33/100= $12.87
So, the discount is $12.87.
Step-by-step explanation: To find the sale price, simply minus the discount from the original selling price:
ie: 39- 12. 87= 26.13
So, the sale price is $26.13
How many different 7-place license plates are possible if the first 2 places are for letters and the other 5 for numbers probability?
Answers
The total number of possible 7-place license plates are 67600000.
Given: A 7-plate license plate. 2 places are for letters and 5 places are for numbers. To find how many different 7-plate license plates are possible
Let's solve the given problem:
The license plate has 7 places. 2 places are for letters and the remaining 5 places are for numbers.
Combination of letters: As there are no restrictions given in the question, so the first letter can be any alphabet out of the 26 alphabets (A, B, C, D, ......... Z). So the first place for the letter can be filled in ²⁶C₁ ways that are 26 ways. Also for the second place, as the letters can repeat so it can be filled in ²⁶C₁ ways too which are 26 ways. Therefore, the possible ways in which the place for two letters can be filled is 26 × 26 ways = 676 ways.Combination of numbers: As there are no restrictions given in the question so the first number can be any of the numbers out of the 10 numbers (10, 1, 2, 3, ....... 9). So the first number can be filled in ¹⁰C₁ = 10 ways. Similarly, as the numbers can repeat so the 2nd, 3rd, 4th and 5th numbers can be filled in ¹⁰C₁ ways that all the other places can be filled in 10 ways each. Therefore the total number of ways in which the place for 5 numbers can be filled is 10 × 10 × 10 × 10 × 10 ways = 100000 ways.Therefore, the total number of ways in which the 7-place license plate can fill are: Total possible ways in which the two letters can be filled × Total possible ways in which the 5 number places can be filled
= 676 × 100000
= 67600000 ways
Hence the total number of possible 7-place license plates are 67600000.
Know more about "permutations and combinations" here: https://brainly.com/question/13387529
#SPJ6
Solve each equation. Check your solutions. x /2 = x + 1/4
Answers
⊂ Hey, ausemkattom2559 ⊃
Answer:
x = 1
Step-by-step explanation:
Given:Solve each equation.
Check your solutions.
x /2 = x + 1/4
Solving:
From the given: \(\frac{x}{2}=\frac{x+1}{4}\)
Applying fraction cross multiply: \(\mathrm{if\;\frac{a}{b}=\frac{c}{d}\mathrm{\:then\:}a\cdot \:d=b\cdot \:c}\)
\(x\cdot \:4=2\left(x+1\right)\)
Distribute:
\(x\cdot \:4=2x+2\)
Subtract 2x from both sides:
\(x\cdot \:4-2x=2x+2-2x\)
\(2x=2\)
Divide both sides by 2:
\(\frac{2x}{2}=\frac{2}{2}\)
x = 1
As a result, x = 1
Check Answer:
We can substitute to check our solution:
1/2 = 1 + 1/4
1/2 = 1/2
Hence, x = 1
xcookiex12
9/12/2022
Which expression is equivalent to 586c + 736c, if c+ 0?

Answers
Answer:
C.
\(12 \sqrt[3]{6c} \)
Step-by-step explanation:
\(5 \sqrt[3]{6c} + 7 \sqrt[3]{6c} \\ = (5 + 7)( \sqrt[3]{6c}) \\ = 12 \sqrt[3]{6c} \)
la) 43 - 2x = 11 its regular equations
Answers
Answer:
x = 16
Step-by-step explanation:
Hope this helps!!
Please help meeeeeee

Answers
Answer: An arithmetic sequence has a constant difference between each term.
For example: 2,4,6,8,10,12,…
We can see clearly that all the terms differ by +2.
We call this the common difference, d.
A geometric sequence has a constant ratio (multiplier) between each term.
An example is: 2,4,8,16,32,…
So to find the next term in the sequence we would multiply the previous term by 2.
This is called the common ratio, r.
These sequences are closely related as they both have the same first term, but I hope you can see how different they become if they have a common difference or a common ratio.
We can create a decreasing arithmetic sequence by choosing a negative common difference.
Similarly, a decreasing geometric sequence would have a common ratio of less than 1.
Step-by-step explanation: I think that should answer for you.
Flagpole The world's tallest unsupported flagpole is a 282-ft-tall steel pole in
Surrey, British Columbia. The shortest shadow cast
by the pole during the year
is 137 ft long. To the nearest degree, what is the angle of elevation of the sun
when the shortest shadow is cast?
Answers
Check the picture below.
\(tan(\theta )=\cfrac{\stackrel{opposite}{282}}{\underset{adjacent}{137}}\implies \theta =tan^{-1}\left( \cfrac{282}{137} \right)\implies \theta \approx 64^o\)
Make sure your calculator is in Degree mode.

What is the missing step in solving the inequality 4(x – 3) + 4 < 10 + 6x? 1. The distributive property: 4x – 12 + 4 < 10 + 6x 2. Combine like terms: 4x – 8 < 10 + 6x 3. The addition property of inequality: 4x < 18 + 6x 4. The subtraction property of inequality: –2x < 18 5. The division property of inequality: ________ x < –9 x > –9 x < x is less than or equal to negative StartFraction 1 Over 9 EndFraction. x > –x is greater than or equal to negative StartFraction 1 Over 9 EndFraction.
Answers
The inequality 4(x – 3) + 4 < 10 + 6x is solved as x > -9. Then the variable x is greater than the negative 9. Then the correct option is B.
What is inequality?Inequality is defined as an equation that does not contain an equal sign.
The inequality equation is given below.
4(x – 3) + 4 < 10 + 6x
Then the steps of solving are given below.
1. The distributive property: 4x – 12 + 4 < 10 + 6x
2. Combine like terms: 4x – 8 < 10 + 6x
3. The addition property of inequality: 4x < 18 + 6x
4. The subtraction property of inequality: –2x < 18
5. The division property of inequality: x > –9
Then x is greater than the negative 9.
Then the correct option is B.
More about the inequality link is given below.
https://brainly.com/question/19491153
#SPJ1
the early income of a girl is rupees 150000 the tax free allowance is rupees 100000 if the text for the first rupees 20000 is 12% and for the remaining is 15% how much tax should she pay in a year ?
Answers
Answer:
Rs 6900
Step-by-step explanation:
To calculate the tax amount the girl should pay in a year, we need to determine the taxable income and then apply the corresponding tax rates.
The taxable income is calculated by subtracting the tax-free allowance from the girl's early income:
Taxable Income = Early Income - Tax-Free Allowance
Taxable Income = 150,000 - 100,000
Taxable Income = 50,000
Now, we can calculate the tax amount based on the given tax rates:
For the first 20,000 rupees, the tax rate is 12%:
Tax on First 20,000 = 20,000 * 0.12
Tax on First 20,000 = 2,400
For the remaining taxable income (30,000 rupees), the tax rate is 15%:
Tax on Remaining 30,000 = 30,000 * 0.15
Tax on Remaining 30,000 = 4,500
Finally, we add the two tax amounts to get the total tax she should pay in a year:
Total Tax = Tax on First 20,000 + Tax on Remaining 30,000
Total Tax = 2,400 + 4,500
Total Tax = 6,900
Therefore, the girl should pay 6,900 rupees in tax in a year.
What Is the fraction 3/8+1/6
Answers
Answer:
13/24
Step-by-step explanation:
3/8 + 1/6
We need to get a common denominator of 24
3/8 *3/3 + 1/6*4/4
9/24 + 4/24
13/24
Find the missing integer that makes the statement true.
____+(-3) = 2

Answers
Explanation:
Think of the problem as x-3 = 2 where x is the blank that we need to fill in.
Adding on -3 is the same as subtracting 3, so that's why x+(-3) is the same as x-3.
To solve x-3 = 2, we add 3 to both sides and we'll get x = 5
Then note how 5-3 = 2 to help confirm the answer.
Answer:
5
Step-by-step explanation:
5 + (-3) = 5 - 3
A 95% confidence interval for the population mean implies that if samples are drawn repeatedly and confidence intervals for μ are constructed, then 95% of the confidence intervals computed will contain the population mean (true or false)
Answers
True.
A 95% confidence interval for the population mean means that if we draw multiple samples from the same population and construct confidence intervals for the mean using each sample, then 95% of those intervals will contain the true population mean. This is because the confidence interval is computed based on the sample mean and the sample's standard deviation, which are random variables that are expected to vary from sample to sample. Therefore, we cannot be 100% certain that the true population mean is within any particular confidence interval, but we can be confident (95% confident, in this case) that most of the intervals we construct will contain the true mean. A 95% confidence interval for the population mean implies that if samples are drawn repeatedly and confidence intervals for μ are constructed, then 95% of the confidence intervals computed will contain the population mean. This means that you can be 95% confident that the true population mean lies within the calculated interval.
Learn more about standard deviation here: brainly.com/question/23907081
#SPJ11
answerrrrrr plssss ill giveee brainliesttttt

Answers
\(m\angle E=\sin \dfrac{\sqrt{10}}{2\sqrt5}=\sin \dfrac{\sqrt2}{2}=45^{\circ}\)
Find all the second order partial derivatives of the given function. f(x, y) = x^2 + y - e^x + y^2 f/x^2 = 1 - e^x + y;^2 f/y^2 = -e^x + y;^2f/y x =^f/x y = -e^x + y^2 f/x^2 = 2 - e^x + y;^2 f/y^2 = -e^x + y;^2f/y x =^f/x y = -e^x + y^2 f/x^2 = 2 - y^2 e^x + y;^2 f/y^2 = -x^2 e^x + y;^2f/y x =^f/x y = -y^2 e^x + y^2 f/x^2 = 2 + e^x + y;^2 f/y^2 = -e^x + y;^2f/y x =^f/x y = -e^x + y Solve the problem. Evaluate dw/dt at t = 1/2 pi for the function w(x, y) = x^2 - y^2 + 10x; x = cost, y = sin t. a)6 b)-10 c)3 d)8
Answers
The second-order partial derivatives of \(\(f(x, y) = x^2 + y - e^x + y^2\)\)are:
\(\(\frac{{\partial^2 f}}{{\partial x^2}} = 2 - e^x\), \(\frac{{\partial^2 f}}{{\partial y^2}} = 2\),\(\frac{{\partial^2 f}}{{\partial x \partial y}} = 0\),\(\frac{{\partial^2 f}}{{\partial y \partial x}} = 0\)\) . The value of \(\(w(x, y) = x^2 - y^2 + 10x\)\) at \(\(t = \frac{1}{2}\pi\)\) is -1. The value of \(\(\frac{{dw}}{{dt}}\)\)at \(\(t = \frac{1}{2}\pi\)\) is -10.
The second-order partial derivatives of the function f(x, y) = x² + y - eˣ+ y² are as follows:
The second partial derivative with respect to x, denoted by (∂²f)/(∂x²), evaluates to 2 - eˣ. This derivative represents the rate of change of the rate of change of f with respect to x.
The second partial derivative with respect to y, (∂²f)/(∂y²), simplifies to 2. It represents the rate of change of the rate of change of f with respect to y. The mixed partial derivatives, (∂²f)/(∂x∂y) and (∂²f)/(∂y∂x), both evaluate to 0. This indicates that the order of differentiation does not affect the result, implying symmetry in the mixed partial derivatives.
To evaluate the function \(w(x, y) = x^2 - y^2 + 10x\) at t = 1/2π, we substitute x = cos(t) and y = sin(t). Substituting these values into the expression for w yields w(cos(t), \(sin(t)) = cos^2(t) - sin^2(t) + 10cos(t)\). Plugging in t = 1/2π, we find w(0, 1) = -1.
Finally, to find dw/dt at t = 1/2π, we differentiate w with respect to t and substitute t = 1/2π. By taking the derivative, we obtain dw/dt = -2sin(t)cos(t) - 2sin(t)cos(t) - 10sin(t). Substituting t = 1/2π gives dw/dt|t=1/2π = -10.
Learn more about derivative here: https://brainly.com/question/32963989
#SPJ11
Please Helpp Asap It’s due Tomorrow

Answers
Answer:
y = 2.5
Step-by-step explanation:
if y = 0
x= 2.5
u do the y as 0 and x as 2.5
and then draw a straight line
Data where the difference between data values has meaning but there is no defined starting point
Answers
Examples of such data include stock prices, economic indicators, and meteorological data such as temperature, wind speed, and barometric pressure.
These types of data often have a trend or pattern, but the difference between the data points has meaning and does not necessarily have a defined starting point.
1. Data where the difference between data values has meaning but there is no defined starting point can be defined as data that is not linearly dependent.
2. Examples of such data include stock prices, economic indicators, and meteorological data. These types of data often have a trend or pattern, but the difference between the data points has meaning and does not necessarily have a defined starting point.
3. Stock prices, economic indicators, and meteorological data all have different scales and can move in different directions, making it difficult to track the exact difference between data points.
4. Despite this, these types of data still allow for meaningful analysis and can be used to make predictions and draw conclusions.
Learn more about data here
https://brainly.com/question/14893265
#SPJ4
I forgor to add the options for the term part, please help!!! 45 points, please only choose from the options..

Answers
This is due tomorrow
April 20-2023
If you help thank you! :)

Answers
Answer:
54 cm squared
Step-by-step explanation:
8 x 5 = 40cm
7 x 2 = 14cm
14 cm + 40 cm = 54 cm squared
What is the measure of RST?
A. 77°
B. 62°
C. 47°
D. 124
Answers
The calculated measure of RST in the circle is (b) 62
Calculating the measure of RST in the circleFrom the question, we have the following parameters that can be used in our computation:
The circle
Assuming that all lines which appear tangent are actually tangent, we have the following equation
RST = 1/2 * (47 + 77)
The above equation is theorem of angle between two chords
So, we have
RST = 1/2 * 124
Evaluate
RST = 62
Hence, the value of RST in the circle is (b) 62
Read more about circle at
brainly.com/question/25871159
#SPJ1

there are two separate stacks of circular coins. the first stack has h coins stacked ontop of each other to form a cylinder. the second stack has h coins stacked on top of each other to form an oblique cylinder.do the cylinders have the same volume? why or why not?
Answers
The cylinders formed by stacking circular coins on top of each other will not have the same volume if they are formed in different ways. In this case, the first stack forms a cylinder with a vertical axis, while the second stack forms an oblique cylinder with an axis that is not vertical.
The volume of a cylinder is given by the formula V = πr^2h, where r is the radius of the base and h is the height of the cylinder. Since both stacks have the same number of coins stacked on top of each other (h coins), the height of both cylinders will be the same. However, the radius of the base will be different for the two cylinders.
In the case of the first stack, the coins are stacked directly on top of each other to form a cylinder with a base that is perfectly circular. Therefore, the radius of the base is the same for every coin in the stack. This means that the radius of the base of the cylinder will be constant, and the volume of the cylinder will only depend on the height.
On the other hand, in the case of the second stack, the coins are not stacked directly on top of each other. Instead, they are arranged in a slanted manner, forming a base that is not perfectly circular. As a result, the radius of the base will vary depending on the position of the coin in the stack. This means that the volume of the oblique cylinder will depend on both the height and the varying radius of the base.
Therefore, the cylinders formed by the two separate stacks of circular coins will have different volumes due to the difference in the base shape and the varying radius of the base in the oblique cylinder.
To learn more about oblique cylinder :brainly.com/question/30941473
#SPJ11
please help me!! confused lol

Answers
Answer: y= -3x -1
you should calculate the gradient of the line using the points shown in the question (-1, 2) and (1, -4)
Gradient formula: \(m = \frac{y2-y1}{x2-x1}\) (next you should substitute the values from
the points)
\(m= \frac{2-(-4)}{-1-1} \\m=-3\)
Please help me with this geometry question

Answers
4x6x2=48 this is the cut out area
7x10x2=140 this is it all together
140-48=92 this is the area of the shaded area
Pls tell me if I'm wrong
Have a good day! :)
Doubling the size of the sample will a. double the standard error of the mean b. have no effect on the standard error of the mean c. reduce the standard error of the mean to approximately 70% of its current value d. reduce the standard error of the mean to one-half its current value
Answers
Using the Central Limit Theorem, it is found that the correct option regarding the standard error of the mean is given by:
c. reduce the standard error of the mean to approximately 70% of its current value.
What does the Central Limit Theorem states about the standard error of the mean?By the Central Limit Theorem, the sampling distribution of sample means of size n has standard error \(s = \frac{\sigma}{\sqrt{n}}\).
Doubling n, we have that:
\(s_d = \frac{\sigma}{\sqrt{2n}} = \frac{1}{\sqrt{2}}\left(\frac{\sigma}{\sqrt{n}}\right) = 0.7\left(\frac{\sigma}{\sqrt{n}}\right) = 0.7s\)
Hence option C is correct.
More can be learned about the Central Limit Theorem at https://brainly.com/question/24663213
#SPJ1
a tennis player hits the ball with an initial speed of 58 feet per second at an angle of 19°, from a height of 1.9 feet. how far away does the ball land in feet? 63.495 feet 65.369 feet 69.836 feet 71.437 feet
Answers
The tennis player hits the ball with an initial speed of 58 feet per second at an angle of 19°, from a height of 1.9 feet. The ball lands at a distance of 65.369 feet from the initial point.
We need to determine how far away the ball land in feet. The horizontal and vertical motions of the ball are independent of each other. The horizontal motion is unaffected by the vertical motion of the ball. It means the ball will move with a constant horizontal velocity of Vx = Vo × cos θ
Where
Vx is the horizontal velocity
Vo is the initial velocity
θ is the angle of the velocity vector with respect to the horizontal axis
Thus, the horizontal component of the initial velocity is given by:
Vx= 58 ft/s cos (19°)
Vx = 55.4 ft/s
Similarly, the vertical component of the initial velocity is given by:
Vy = Vo × sin θ
Vy = 58 ft/s sin (19°)
Vy = 18.8 ft/s
The time of flight (t) can be found using the vertical motion of the ball. Using vertical motion, the distance traveled in the horizontal direction can be found using
d = Vx × t.
The time of flight can be calculated as
t = 2Vy / g
where g is the acceleration due to gravity,g = 32.2 ft/s
2t = 2(18.8) / 32.2
t = 1.16 s
Therefore, the distance traveled in the horizontal direction can be calculated as:
d = Vx × td
= 55.4 × 1.16d
= 64.1 feet
The ball lands at a distance of 64.1 feet from the initial point. Hence, the correct option is 65.369 feet (rounded off to three decimal places).
You can learn more about the initial speed at: brainly.com/question/12787359
#SPJ11
The question asks about the range of a tennis ball hit under specific conditions. Using the formula for the range of a projectile, and the given values for speed, angle, and gravity, it is found that the tennis ball will land approximately 63.495 feet away.
Explanation:The subject of the question is Physics, specifically kinematics, and the motion of projectiles. This is a problem of projectile motion. We will determine where the tennis ball lands in terms of horizontal distance also known as range.
To calculate the range, we use the formula: Range = (v² sin (2θ)) / g, where v is the initial velocity of the ball, θ is the angle at which it's thrown, and g is the acceleration due to gravity. Here, v= 58 feet per second, θ= 19°, and g= 32.2 feet/second² respectively.
Through calculations, we will find that the tennis ball lands approximately 63.495 feet away from the starting point.
Learn more about Projectile Motion here:https://brainly.com/question/20627626
#SPJ12
What does an expression never have.
A.variables
B.numbers
C.equals sign
Answers
Answer:
C
Step-by-step explanation:
An Expression has no equal sign, because it is not complete. Yet an equation does.
Please help me I am really confused and need help with this.

Answers
Answer:
Step-by-step explanation:
y=10