How to find the median of even number of data ? A. you must list the data in order from least to greatest. Then calculate the mean of the smallest and largest numbers to find the median of the set. B. you must list the data from least to greatest. Then calculate the mean of the middle two data points to find the median. of the set. C. To find the median of the set , calculate the mean of the middle two data points . D. You must list the data in order from least to greatest. Then divide the mean of the set by 2. to find the median of the set.
Answers
Answer:
D
Step-by-step explanation:
is the answer...if you have an odd number divide by 2 and round up and if you have an even number divide by 2.
The value of the middle-most observation obtained after arranging the data in ascending order is called the median of the data.
What is median of data?The median is the value in the middle of a data set, meaning that 50% of data points have a value smaller or equal to the median and 50% of data points have a value higher or equal to the median. For a small data set, you first count the number of data points (n) and arrange the data points in increasing order.
The median represents the middle value for any group. It is the middle value of a sorted list of given numbers.
For an even set of numbers Median = ((n/2)th observation+(n/2 +1)th observation)/2
Therefore, the value of the middle-most observation obtained after arranging the data in ascending order is called the median of the data.
Learn more about the median here:
https://brainly.com/question/28060453.
#SPJ6
Related Questions
Suppose the given confidence level is 85%, what is the corresponding z critical value?
Answers
Given:
A. sin(x)
B. cos(x)
C. cos(y)
D. sin(y)
Use the drop-down menus in the derivation of the sine sum identity:
sin(x + y)
= cos (StartFraction pi Over 2 EndFraction minus (x + y))
= Cosine ((StartFraction pi over 2 EndFraction minus x) minus y)
= Cosine (StartFraction pi Over 2 EndFraction minus x)
A
+ Sine (StartFraction pi Over 2 EndFraction minus x)
A
sin(x)cos(y) + cos(x)sin(y)
Answers
Trigonometric functions can be simply defined as the functions of an angle of a triangle.
The basic trigonometric functions are sine, cosine, tangent, cotangent, secant and cosecant.
sine sum identity: \(sin(x+y)=sin(x)cos(y)+cos(x)sin(y)\)
In sine sum identity , sin(x), cos(x), sin(y) and cos (y) is used.
Some identities shown below,
\(sin(x-y)=sin(x)cos(y)-cos(x)sin(y)\\\\cos(x-y)=cos(x)cos(y)+sin(x)sin(y)\\\\\\cos(x+y)=cos(x)cos(y)-sin(x)sin(y)\\\\\)
Learn more:
https://brainly.com/question/20094605
Answer:
C, D
Step-by-step explanation:
Y=x^3Can you please give a graph use color for function, asymptotes, etc.A short table of easy pointsThe domain and rangePlease identify and label the asymptotes (please work this as if you didn’t have a calculator)
Answers
ANSWER
STEP-BY-STEP EXPLANATION
Given information
\(y=x^3\)Step 1: Graph the above function
Step 2: Find the asymptotes?
The asymptotes of the given function are zero because the function is not a rational function.

use the point-slope form to find the ewuation of the line through the points (-5,2) and (-2,6)
Answers
Answer:
The equation of the line through the points (-5, 2) and (-2, 6) is \(y = \frac{4}{3}\cdot x +\frac{26}{3}\).
Step-by-step explanation:
The point-slope form of the equation of the line is defined by this formula:
\(y-y_{1} = m\cdot (x-x_{1})\) (1)
Where:
\(x\) - Independent variable.
\(y\) - Dependent variable.
\(m\) - Slope.
\(x_{1}\), \(y_{1}\) - Coordinates of the first point.
In addition, the slope of the line can be determined in terms of two distinct points:
\(m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) (2)
Where \(x_{2}\), \(y_{2}\) are the coordinates of the second point.
If we know that \(x_{1} = -5\), \(y_{1} = 2\), \(x_{2} = -2\) and \(y_{2} = 6\), then the equation of the line is:
\(m = \frac{6-2}{-2-(-5)}\)
\(m = \frac{4}{3}\)
\(y-2 = \frac{4}{3}\cdot (x+5)\)
\(y = \frac{4}{3}\cdot x +\frac{26}{3}\)
The equation of the line through the points (-5, 2) and (-2, 6) is \(y = \frac{4}{3}\cdot x +\frac{26}{3}\).
for a repair job an electrician charges an hourly rate of d dollars plus a flat fee of 50 the electricion charged a total if 114 for a 4-hour repair job. Part B. What is the value of D

Answers
Answer:
B. 4d + 50 = 114
Step-by-step explanation:
Given parameters:
Hourly rate = $d/hr
Flat fee = $50
Charge for the 4hrs = $114
Number of hours = 4hrs
To find d;
Total cost = $114;
$114 = Flat fee + (rate per hour x number of hours)
$114 = $50 + 4d
The value of d can be calculate using;
4d + 50 = 114
The value of d is 4d + 50 = 114
A marching band performs on the football field at half-time. As they perform, the members of the band stand in
the shape of a sinusoidal function. While playing, they move, but still maintain the sinusoidal function,
transforming it in different ways.
Darla is a member of the marching band. As the band begins to play she is positioned in the exact center of the
field. The person closest to her on the same horizontal line, stands 10 yards away. The sinusoidal function
extends to the ends of the playing field.
The playing area of football field measure 300 feet by 160 feet. Place the playing area of a football field on the
coordinate plane such that the origin is the lower left comer of the football field.
(Score for Question 1: of 2 points)
1. What is the period and the amplitude of the sine function representing the position of the band members as
they begin to play?
Answer.
Answers
The period of the sine function representing the position of the band members is 60 feet, and the amplitude is approximately \(170.3 feet.\)
What is the coordinate plane?Since the band members are standing in the shape of a sinusoidal function, we can assume that their positions can be represented by the equation:
\(y = A sin(Bx)\)
where y is the vertical position of a band member, x is the horizontal position on the field, A is the amplitude, and B is the period.
Since Darla is positioned in the exact center of the field, and the person closest to her on the same horizontal line stands 10 yards away, we can assume that the sinusoidal function has a phase shift of 0. This means that the midline of the function passes through the point (0, 0).
To find the amplitude, we need to determine the maximum and minimum heights of the function.
Since the playing area of the football field measures 300 feet by 160 feet, the distance between the two farthest points on the field is the diagonal distance, which can be calculated using the Pythagorean theorem:
\(sqrt(300^2 + 160^2) \approx 340.6 feet\)
Since the distance between the farthest points on the field is equal to the distance between two peaks or two valleys of the sinusoidal function, the amplitude is half of this distance:
\(A = 340.6/2 \approx170.3 feet\)
To find the period, we can use the fact that the distance between two consecutive peaks or valleys is equal to the period of the function.
Since the person closest to Darla stands 10 yards away, or 30 feet away, we can assume that this person is standing at a peak or a valley of the function. This means that the period is twice the distance between Darla and the person closest to her:
\(P = 2(30) = 60 feet\)
Therefore, the period of the sine function representing the position of the band members is 60 feet, and the amplitude is approximately \(170.3 feet.\)
Learn more about coordinate here:
https://brainly.com/question/16634867
#SPJ9
Table I contains outputs of the function f(x) = b* for some 2 values, and Table Il contains outputs of the
function g(x) = log: (x) for some e values. In both functions, b is the same positive constant.
Fill in the missing values in the tables. If necessary, round your answer to three decimal places.

Answers
Table 1: 1.683 Table 2: 9
The missing values in the table will be 11.452.
What is a logarithm?Logarithms are another way of writing exponent. A logarithm with a number base is equal to the other number. It is just the opposite of the exponent function.
The given data from the table;
\(\rm f(x)=b^x\)
For the first function;
\(\rm b^(0.683)= 3 \\\\ b= 4.995\)
The blank data is found as;
\(\rm b^x = 8 \\\\ \rm (4.995)^x = 8 \\\\ x \ log \ 4.995 =8 \\\\ x=11.452\)
Hence the missing values in the table will be 11.452.
To learn more about the logarithm refer to the link;
https://brainly.com/question/7302008
Determine whether each statement below is true or false. Justify each answer. a. The equation Axb is referred to as a vector equation. Choose the correct answer below. A. False. The equation Axb is referred to as a matrix equation because A is a matrix. B. True. The equation Axb is referred to as a vector equation because A is constructed from column vectors. C. True. The equation Axb is referred to as a vector equation because it consists of scalars multiplied by vectors. D. False. The equation Axb is referred to as a linear equation because b is a linear combination of vectors.
Answers
What is the distance, rounded to the nearest tenth, between the points (-2,4) and (6,-4)?
Answers
HOPE ITS HELP
A small plane travels at 450 miles in 3 hours. At this rate, how far can it travel in 7 hours?
Answers
Answer:
1050 miles
Step-by-step explanation:
velocity=distance/time
Distance=450 miles
Time=3 hours
Velocity=150 miles/hours
if time is 7 and velocity is 150 distance is 7x150=1050 miles
Last week, a candy store sold 6 1/3
pounds of white chocolate. It sold 4 times as much milk chocolate as white chocolate. DUE NOWW HELP
Question 1
How many pounds (in mixed number form) of milk chocolate did the candy store sell last week?
Responses
A 24 2/3
B. 25 2/3
C. 25 1/3
D. 24 1/3
Question 2
How many more pounds of milk chocolate were sold than white chocolate at the candy store last week?
Responses
A. 19 2/3
B. 18
C. 19
D. 18 2/3
Answers
1)The number of milk chocolate that sold last week is = \(25\frac{2}{3}\) B is correct
2)white chocolate at the candy store last week is 19.
Last week, a candy store sold \(5\frac{1}{3}=\frac{16}{3}\) pounds of white chocolate. It sold 4 times as much milk chocolate as white chocolate.
The number of milk chocolate did the candy store sell last week.
Since the candy store sold 4 times as much milk chocolate as white chocolate, it sold:
\(4 *\frac{ 19}{3 } =\frac{ 76}{3}\\ pounds\ of\ milk\ chocolate.= 25 \frac{2}{3}\)
option B is correct.
2)
To find out how many more pounds of milk chocolate were sold than white chocolate at the candy store last week, we can subtract the amount of white chocolate sold from the amount of milk chocolate sold:
\(\frac{76}{3} - \frac{19}{3} \\= \frac{57}{3}\\ = 19\ pounds.\)
option C is correct
learn more about the number
https://brainly.com/question/17429689
#SPJ1
Which ordered pair solves this linear system?
Y= -x
Y= 2x
Answers
The ordered pair that solves the system of equation is (0, 0).
To solve this system, we can substitute the first equation into the second equation to eliminate y:
x = 2x
Solving for x, we get x = 0.
Substituting x = 0 into the first equation, we get y = 0.
Therefore, the ordered pair that solves the system is (0, 0).
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Solve the system by substitution.5x - 2y + 3z =62x - 4y - 3z = - 23X + 6y - 8z = 1X =Y =Z =
Answers
X=1
Y=4
Z=3
Explanation
\(\begin{gathered} 5x-2y+3z=6\Rightarrow equation(1) \\ 2x-4y-3z=-23\Rightarrow equation(1) \\ x+6y-8z=1\Rightarrow equation(1) \end{gathered}\)
Step 1
b) isolate the x variable in equaiton (1) and equation(2)
so
\(\begin{gathered} 5x-2y+3z=6\Rightarrow equation(1) \\ \text{add 2y in both sides} \\ 5x-2y+3z+2y=6+2y \\ 5x+3z=6+2y \\ \text{subtract 3z in both sides} \\ 5x+3z-3z=6+2y-3z \\ 5x=6+2y-3z \\ \text{divide both sides by 5} \\ \frac{5x}{5}=\frac{6+2y-3z}{5} \\ x=\frac{6+2y-3z}{5}\Rightarrow equation(1A) \end{gathered}\)and
\(\begin{gathered} 2x-4y-3z=-23\Rightarrow equation(2) \\ 2x=-23+4y+3z \\ x=\frac{-23+4y+3z}{2} \end{gathered}\)b) now replace x value from equaton (1) into equation (3)
\(\begin{gathered} x+6y-8z=1 \\ \frac{6+2y-3z}{5}+6y-8z=1 \\ \frac{6+2y-3z}{5}=1-6y+8z \\ 6+2y-3z=5(1-6y+8z) \\ 6+2y-3z=5-30y+40z \\ 6-5+2y+30y-3z-40z=0 \\ 1+32y-43z=0 \\ 32y-43z=-1\Rightarrow equation(4) \end{gathered}\)c) now replace x value from equaton (2) into equation (3)
\(\begin{gathered} x+6y-8z=1 \\ \frac{-23+4y+3z}{2}+6y-8z=1 \\ \frac{-23+4y+3z}{2}=1-6y+8z \\ -23+4y+3z=2(1-6y+8z) \\ -23+4y+3z=2-12y+16z \\ -23+4y+3z-2+12y-16z=0 \\ -25+16y-13z=0 \\ 16y-13z=25\Rightarrow equation(5) \end{gathered}\)Step 2
now, use equation (4) and equation(5) to
\(\begin{gathered} 32y-43z=-1\Rightarrow equation(4) \\ 16y-13z=25\Rightarrow equation(5) \end{gathered}\)a) isolate the y value from equation(1) and substitute into equation(2)
z=
\(\begin{gathered} 32y-43z=-1\Rightarrow equation(4) \\ 32y=-1+43z \\ y=\frac{-1+43z}{32} \\ \text{replace in eq(5)} \\ 16y-13z=25\Rightarrow equation(5) \\ 16(\frac{-1+43z}{32})-13z=25 \\ (\frac{-1+43z}{2})-13z=25 \\ (\frac{-1+43z}{2})=25+13z \\ -1+43z=2(25+13z) \\ -1+43z=50+26z \\ 43z-26z=50+1 \\ 17z=51 \\ z=\frac{51}{17} \\ z=3 \end{gathered}\)so
Z= 3
b) replace the z value in equation (4) to find z
\(\begin{gathered} 32y-43z=-1\Rightarrow equation(4) \\ 32y-43(3)=-1 \\ 32y=-1+129 \\ 32y=128 \\ y=4 \\ \end{gathered}\)Y=4
c) finally,l replace the Z and Y value in equation (1A)
\(\begin{gathered} x=\frac{6+2y-3z}{5}\Rightarrow equation(1A) \\ x=\frac{6+2(4)-3(3)}{5} \\ x=\frac{6+8-9}{5}=\frac{5}{5}=1 \end{gathered}\)so
X=1
therefore, the answer is
X=1
Y=4
Z=3
I hope this helps you
Find the missing number in the following fraction calculation
/7 ÷10 =3/35
Answers
x=6
Step-by-step explanation:
x ÷ 7 ÷10 = 3/35
(Use trial & error - since I knew x<7)
6/7 ÷ 10 = 3/35
Or
3/35 x 10
(then, simplify it to 6/7 or ÷ that by 1/7 to get 6)
Hope this helps!
g (3 points)Set up but do no solve the integral required to calculate the volume formed by rotating the region bounded by f(x) = 1/x,g(x) = 1/x^3, andx= 2, andx= 4 around they-axis. Also draw a picture of the region (non-revolved).
Answers
Answer:
Hello,
Step-by-step explanation:
\(\displaystyleV=2*\pi*\int\limits^4_2 {(\dfrac{1}{x}-\dfrac{1}{x^3} )*x } \, dx \\=2*\pi*\int\limits^4_2 {(1-\dfrac{1}{x^2} ) } \, dx \\=2*\pi* [x+\dfrac{1}{x}]^4_2\\\\\boxed{V=\dfrac{7\pi}{2}}\\\)

Use the Pythagorean Theorem to find the distance between (-3, 4) and (6, 1). Show all calculations.
Answers
Answer:
9.48683
Step-by-step explanation:
using the formula:
d = √((x2-x1)2 + (y2-y1)2)Find the difference between coordinates:
(x2-x1) = (6 - -3) = 9
(y2-y1) = (1 - 4) = -3
Square the results and sum them up:
(9)2 + (-3)2 = 81 + 9 = 90
Now Find the square root and that's your result:
Exact solution: √90 = 3√10
Approximate solution: 9.4868
50 Points! Multiple choice geometry question. Photo attached. Thank you!
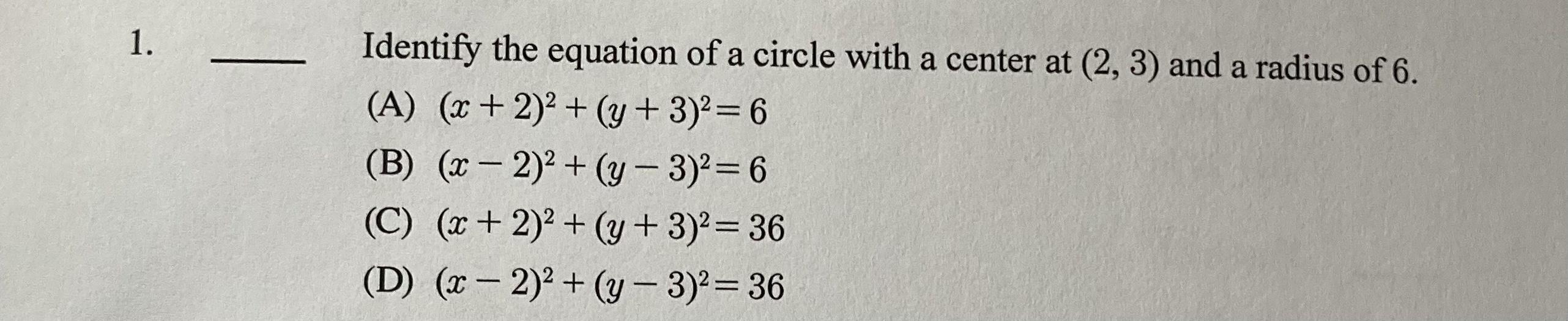
Answers
The equation of the circle is (x - 2)² + (y - 3)² = 36
Determining the equation of the circleFrom the question, we have the following parameters that can be used in our computation:
The circle
Where, we have
Center = (a, b) = (2, 3)
Radius, r = 6 units
The equation of the circle is represented as
(x - a)² + (y - b)² = r²
So, we have
(x - 2)² + (y - 3)² = 6²
Evaluate
(x - 2)² + (y - 3)² = 36
Hence, the equation is (x - 2)² + (y - 3)² = 36
Read more about circles at
brainly.com/question/24810873
#SPJ1
15% of 940 is what number?
Answers
141 multiplied by 15% which can be put into a calculator or workers out as 0.15 is equal to 141 glad to help
Y= 15% * 940
convert to decimal— 0.15
y= 0.15 * 940
y= 141
which geometric figure must have 4 right angles
Answers
Answer: Quadrilateral or if thats not right Square or Rectangle
Step-by-step explanation:
Which of the following statements are true?
Select all that apply.
A. 4 is a perfect cube.
B. 16 is a perfect square.
C. 2,197 is both a perfect square and a perfect cube.
D. 8 is a perfect cube.
E. 18 is neither a perfect square nor a perfect cube.
Answers
The statements that are true are B and D.
Given are some statements we need to check which is true.
Let's analyze each statement:
A. 4 is a perfect cube.
False. 4 is not a perfect cube because there is no integer that can be cubed to give 4.
B. 16 is a perfect square.
True. 16 is a perfect square because it can be expressed as 4^2, where 4 is an integer.
C. 2,197 is both a perfect square and a perfect cube.
False. 2,197 is not a perfect square because there is no integer that can be squared to give 2,197.
However, it is a perfect cube because 13³ equals 2,197.
D. 8 is a perfect cube.
True. 8 is a perfect cube because it can be expressed as 2³, where 2 is an integer.
E. 18 is neither a perfect square nor a perfect cube.
True. 18 is neither a perfect square nor a perfect cube because there is no integer that can be squared or cubed to give 18.
Therefore, the statements that are true are B and D.
Learn more about perfect cube and perfect square click;
https://brainly.com/question/13326108
#SPJ1
The balance on a credit card, that charges a 15.5%
APR interest rate, over a 1 month period is given in
the following table:
Days 1-3: $150 (initial balance)
Days 4-20: $200 ($50 purchase)
Days 21-30: $50 ($150 payment)
What is the finance charge, on the average daily
balance, for this card over this 1 month period?

Answers
Answer:
The finance charge on the average daily balance for this card over the 1 month period is $2.53.
Step-by-step explanation:
To calculate the finance charge, we need to find the average daily balance first. We can do this by adding up the balances for each day and dividing by the number of days in the billing period:
((3 x 150) + (17 x 200) + (10 x 50)) / 30 = 156.67
So the average daily balance is $156.67.
To calculate the finance charge, we can use the following formula:
finance charge = average daily balance x daily periodic rate x number of days
The daily periodic rate is calculated by dividing the APR by 365 days:
daily periodic rate = 0.155 / 365 = 0.00042466
Plugging in the numbers, we get:
finance charge = 156.67 x 0.00042466 x 30 = $2.53
So the finance charge on the average daily balance for this card over the 1 month period is $2.53.
Calculate the rate of change for the table of values.
X
у
2
50
3
75
4.
100
5
125
rate of change =

Answers
Answer:
25
Step-by-step explanation:
50:2=25
75:3=25
100:4=25
125:5=25
The rate of change of the given data in the table will be 25.
What is the rate of change?The momentum of a variable is represented by the rate of change, which is used to mathematically express the percentage change in value over a specified period of time.
The formula for the rate of change is straightforward: it simply divides the current value of a stock or index by the value from a previous time period.
The rate of change will be calculated by using the following formula:-
rate of change = ( y₂ - y₁ ) / ( x₂ - x₁ )
The rate of change will be calculated as below:-
50:2=25
75:3=25
100:4=25
125:5=25
Therefore, the rate of change of the given data in the table will be 25.
To know more about the rate of change follow
https://brainly.com/question/8728504
#SPJ2
The following inequalities represent a system.
y ≥ 5x + 2
y > −3x − 2
Which of the following graphs represents the system?




Answers
See the image linked below.

To graph system of inequalities y ≥ 5x + 2 and y > -3x - 2, draw lines for y = 5x + 2 and y = -3x - 2, then shade areas above each line. The intersection of shaded areas shows solutions to the system of inequalities.
Explanation:In order to graph the system of inequalities y ≥ 5x + 2 and y > -3x - 2 you would start by graphing each inequality as if it was an equality. For the first inequality, you would graph the line y = 5x + 2 and shade the area above the line because it's y 'greater than or equal to'. For the second inequality, you draw the line y = -3x - 2 and also shade the area above because it's y 'greater than'. The intersection of the shaded areas represents the solution to the system of inequalities. Therefore, the graph would have two shaded lines, with the common shaded area above both lines representing the solutions to the system of inequalities.
Learn more about Graphing Inequalities here:https://brainly.com/question/19491153
#SPJ3
For which inequality is x = 5 a solution
Answers
Answer:
4<x<6
Step-by-step explanation:
4 is smaller than x
and x is samller than 6
so its 5
Find the perimeter of this
Tringle
8 cm
7 cm
5 cm
answer is
A. 35 cm
B. 40 cm
C. 20 cm
D. 12.5 cm
Answers
Answer:
C) 20cm
Step-by-step explanation:
Perimeter is the distance around the edge of the shape.
8 + 7 + 5 = 20
Answer:
20 is answer
Step-by-step explanation:
as perimeter= sum of all side
= 8 +7+5=2ocm
saloman was told the written paper on his science experiment should express measurements in liters. Which shows how to calculate the number of liters if he used 5 cups of water
Answers
Answer:
Step-by-step explanation:
Divide 5 by 4.22
Just took the test and this is the right answer
Answer: multiply 5 by 4.22
Step-by-step explanation:
Find the fist 4 terms of a geometric series with first term of 8 and the sum to infinity of 12
Answers
Step-by-step explanation:
the sum of an infinite geriatric series with |r| < 1 is
s = a1/ (1 - r)
in our case we have
a1 = 8
12 = 8/(1 - r)
12(1 - r) = 8
1 - r = 8/12 = 2/3
-r = -1/3
r = 1/3
so, the first 4 terms (I added a5 too, just in case your teacher meant the NEXT 4 terms) are
a1 = 8
a2 = a1 × 1/3 = 8/3
a3 = a2 × 1/3 = 8/9
a4 = a3 × 1/3 = 8/27
a5 = a4 × 1/3 = 8/81
...
Answer:
\(8,\quad \dfrac{8}{3},\quad \dfrac{8}{9},\quad\dfrac{8}{27}\)
Step-by-step explanation:
Sum to infinity of a geometric series:
\(S_\infty=\dfrac{a}{1-r} \quad \textsf{for }|r| < 1\)
Given:
\(a\) = 8\(S_\infty\) = 12Substitute given values into the formula and solve for \(r\):
\(\implies 12=\dfrac{8}{1-r}\)
\(\implies 1-r=\dfrac{8}{12}\)
\(\implies r=1-\dfrac{8}{12}\)
\(\implies r=\dfrac{1}{3}\)
General form of a geometric sequence: \(a_n=ar^{n-1}\)
(where a is the first term and r is the common ratio)
Substitute the found values of \(a\) and \(r\):
\(\implies a_n=8\left(\dfrac{1}{3}\right)r^{n-1}\)
The first 4 terms:
\(\implies a_1=8\left(\dfrac{1}{3}\right)r^0=8\)
\(\implies a_2=8\left(\dfrac{1}{3}\right)r^1=\dfrac{8}{3}\)
\(\implies a_3=8\left(\dfrac{1}{3}\right)r^2=\dfrac{8}{9}\)
\(\implies a_4=8\left(\dfrac{1}{3}\right)r^3=\dfrac{8}{27}\)
Figure A - Figure B. Find the volume of figure B.

Answers
Answer:
use this to help you
Step-by-step explanation:
In math, volume is the amount of space in a certain 3D object. For instance, a fish tank has 3 feet in length, 1 foot in width and two feet in height. To find the volume, you multiply length times width times height, which is 3x1x2, which equals six.
Please Help Marked for all my points and will Brainliest
Different sizes of ribbon need to be cut to go around various shapes. All of the following sizes are in inches.
π,√6,2√6,√7
(a) Without using your calculator, approximate the decimal equivalent of each number to the nearest tenth.
(B) Order the ribbon sizes from least to greatest.
Answers
The requreid,
(a) Approximate values of the given numbers are π ≈ 3.1, √6 ≈ 2.4, 2√6 ≈ 4.8, and √7 ≈ 2.6.
(b) √6 < √7 < π < 2√6
(a)
π ≈ 3.1 (since π is between 3 and 4, and is closer to 3.1 than to 3.2)
√6 ≈ 2.4 (since 6 is between 4 and 9, and the square root of 6 is closer to 2.4 than to 2.5)
2√6 ≈ 4.8 (since 2√6 is approximately twice the value of √6, which is 2.4)
√7 ≈ 2.6 (since 7 is between 4 and 9, and the square root of 7 is closer to 2.6 than to 2.7)
(b)
Order from least to greatest:
√6 < √7 < π < 2√6
Learn more about simplification here:
https://brainly.com/question/9912600
#SPJ1
What is the range of the function f(x) = 4x - 3 given the domain D = {0, 1, 2, 3}?
A. R = {-1, 0, 5, 9}
B. R = {-3, 1, 5, 9}
C.R = {-9, -5, 1, 3}
D.R = {-1, 0, 5, 10}
Answers
The range of the function is R = {-3, 1, 5, 9}.
B. R = {-3, 1, 5, 9}How to find the rangeTo find the range of the function
f(x) = 4x - 3 for the given domain D = {0, 1, 2, 3},
we need to evaluate the function for each value in the domain and list the resulting outputs.
When x = 0, f(0) = 4(0) - 3 = -3
When x = 1, f(1) = 4(1) - 3 = 1
When x = 2, f(2) = 4(2) - 3 = 5
When x = 3, f(3) = 4(3) - 3 = 9
So, the answer is B. R = {-3, 1, 5, 9}.
Learn more about domain at:
https://brainly.com/question/2264373
#SPJ1