How to simply ((4/x)-2)/((1/x)+3)
Answers
\(\cfrac{~~ \frac{4}{x}-2~~}{\frac{1}{x}+3}\implies \cfrac{~~ \frac{4-2x}{\underset{\textit{using this LCD}}{x}}~~}{\frac{1 + 3x}{\underset{\textit{using this LCD}}{x}}}\implies \cfrac{4-2x}{~~\begin{matrix} x \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~ }\cdot \cfrac{~~\begin{matrix} x \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~ }{1+3x}\implies \cfrac{2(2-x)}{1+3x}\)
Related Questions
Factor out the expression: -2xy3 - 8xy2 + xy
Answers
After factoring the given expression -2xy³ - 8xy² + xy, the resultant answer is -2xy²(xy-4).
What are expressions?The concept of algebraic expressions is the use of letters or alphabets to represent numbers without providing their precise values.
A group of terms coupled with the operations +, -, x, or form an expression, such as 4 x 3 or 5 x 2 3 x y + 17.
A statement with an equal sign, such as 4 b 2 = 6, asserts that two expressions are equal in value and is known as an equation.
So, we have the expression:
-2xy³ - 8xy² + xy
Now, factor out as follows:
= -2xy³ - 8xy² + xy
= xy(-2xy² - 8xy)
= -2xy²(xy-4)
Therefore, after factoring the given expression -2xy³ - 8xy² + xy, the resultant answer is -2xy²(xy-4).
Know more about expressions here:
https://brainly.com/question/1859113
#SPJ1
N
50°
AOMN~ ARPQ
Find 0.
M
Ө
0 = [?]°
<
P
70°
R
![N50AOMN~ ARPQFind 0.M0 = [?]<P70R](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/veKTlRrJcwtcPEhjGPeUEj7WPgDpy10G.png)
Answers
Answer:
60°
Step-by-step explanation:
In similar triangles, the corresponding angles are congruent.
∠O = R
O = 70°
In ΔOMN,
∠O + ∠M + ∠N = 180 {Angle sum property of triangle}
70 + 50 + Ф = 180
120 + Ф = 180
Subtract 120 from both sides,
Ф = 180 - 120
Ф = 60°
Write the following expression without negative exponents and without parentheses. 5x^-2
Answers
Solution:
5x^-2
5 * x^-2
5 * 1/x^2
5/x^2
Best of Luck!
The given expression without negative exponent is \(\frac{5}{x^2}\)
Exponents and indicesGiven the indices expression
5x^-2
We are to express with the negative exponent:
According to the indices expression
\(x^{-n}=\frac{1}{x^n}\)
Hence the given expression is \(\frac{5}{x^2}\)
Learn more on indices here; https://brainly.com/question/10339517
Kerry invited 23 friends to his pool party. They played a game where everyone had to separate into groups. Each group had the same number of children.The game could not be played with all 24 children in one group and each group had to have more than two children. Which of the following are ways that they could divide into groups? Choose all that apply.
Answers
Answer:
24:
6 of 4
or
8 of 3
Step-by-step explanation:
6x4=24
8x3=24
help hep help help help help
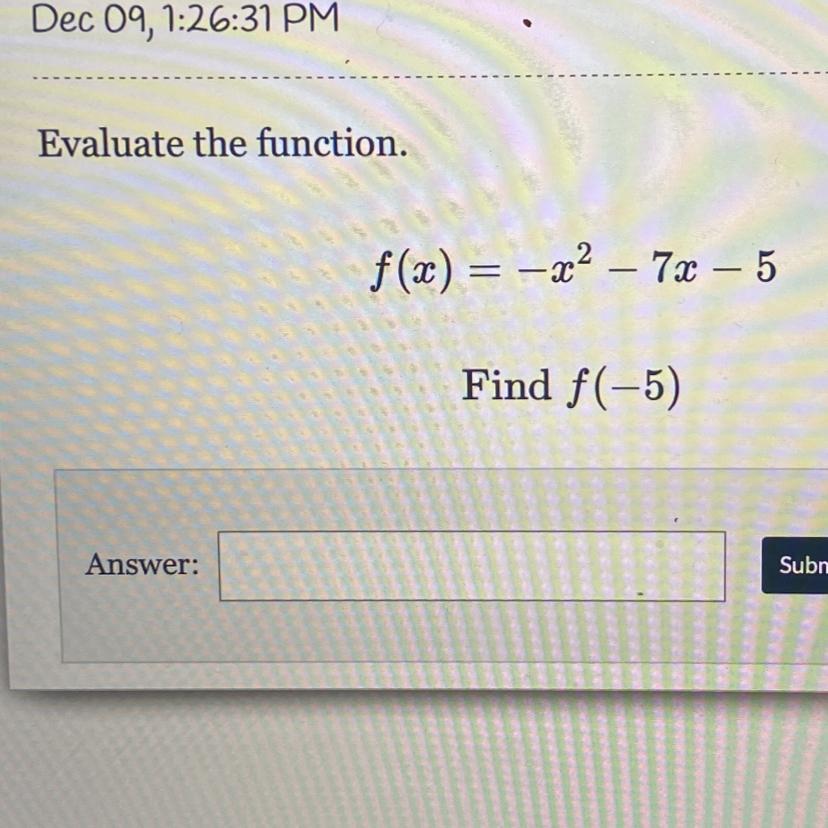
Answers
Answer:
should be 5!
Step-by-step explanation:
100%
Đ
X
A doctor treated 24, 27, 31, 19, 26, 15, and 19 patients during the past 7 days.
Which is the median number of
patients treated by the doctor?
A 15
B. 19
C. 23
D. 24
E. 31

Answers
Answer:
C. 23
Step-by-step explanation:
Add then divide by 7
I need someone to solve b ASAP please help

Answers
b) The 99% confidence interval for the population proportion is given as follows: (0.57, 0.68).
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The confidence level is of 99%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.99}{2} = 0.995\), so the critical value is z = 2.575.
The parameters for this problem are given as follows:
\(n = 520, \pi = \frac{325}{520} = 0.625\)
Then the lower bound of the interval is given as follows:
\(0.625 - 2.575\sqrt{\frac{0.625(0.375)}{520}} = 0.57\)
The upper bound of the interval is given as follows:
\(0.625 + 2.575\sqrt{\frac{0.625(0.375)}{520}} = 0.68\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
Solve for k. simplify the answer
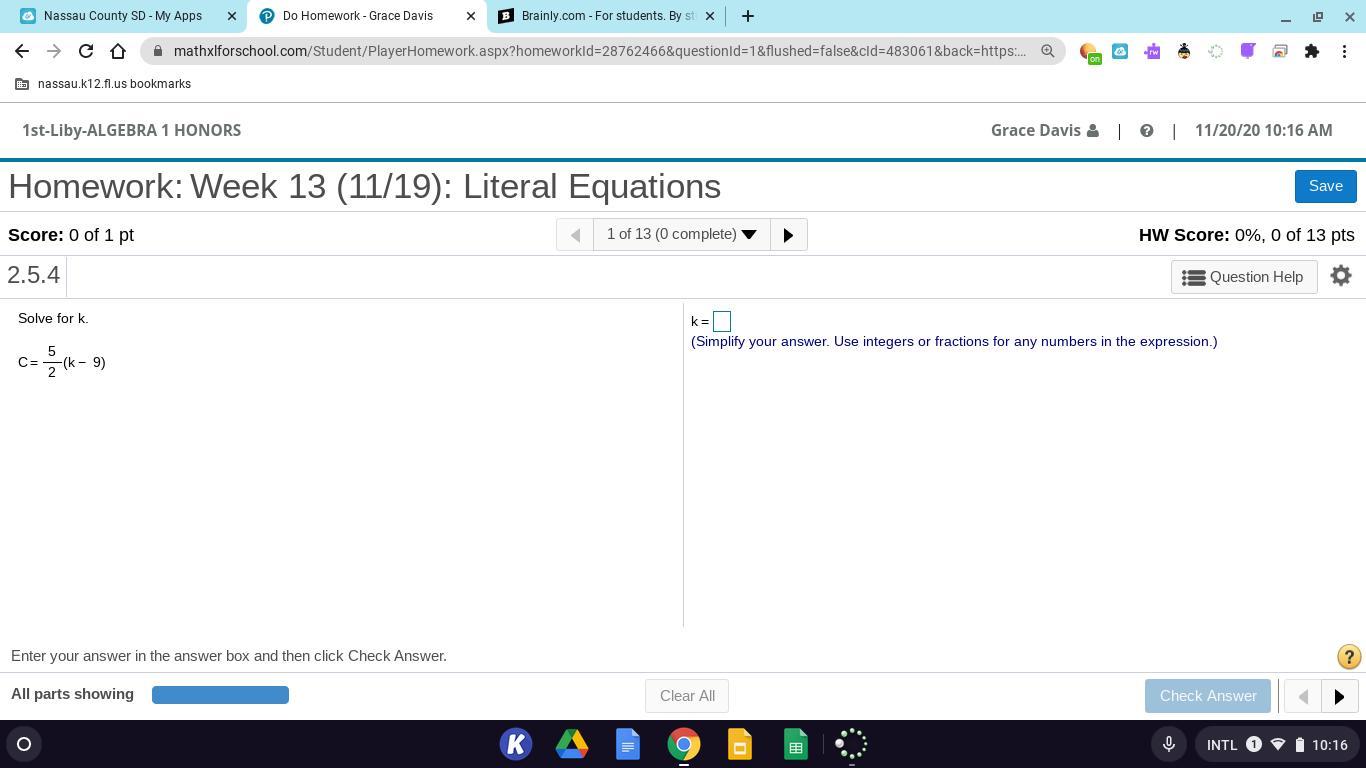
Answers
Answer:
c=5/2k+ −45/2
Step-by-step explanation:
Answer:
K= 9 + 2/5C
Step-by-step explanation:
1. Remove the parentheses
C= 5/2 x (k-9)
2. Multiply both sides
C= 5/2k- 45/2
3. Move the terms
2C= 5k- 45
4. Divide both sides
-5k= -45- 2C
5. Write in parametric form
k=9 + 2/5C
A six sided die is rolled 60 times and the die landed on the number five a total of 12 times.
What is the THEORETICAL probability that the die should land on 5
Answers
Answer:
1/5
Step-by-step explanation: 60/12+48-53+5
The measures of the angles of a triangle are shown in the figure below. Solve
for X.

Answers
Answer:
x = 4
Step-by-step explanation:
The sum of the interior angles of a triangle equal 180.
2x + 15 + 67 + 90 = 180 Combine like terms
2x + 172 = 180 Subtract 172 from both sides
2x + 1752 - 172 = 180 - 172
2x = 8 Divide both sides by 2
\(\frac{2x}{2}\) = \(\frac{8}{2}\)
x = 4
Answer:
x= 4
Step-by-step explanation:
To Find: Angle Measure X67+2x+15+90=180 (Sum of measures of a Triangle)
2x + 172 = 180
2x=180-172
2x=8
x=\(\frac{8}{2}\)
x= 4
Mark Me BrainliestHow many ways can 10 books be arranged on a shelf?
Answers
Place them horizontally or vertically
Which graph shows an increasing linear function? p.s dont mind the tabs lol!!!

Answers
According to R.L. Polk & Co., the average age of cars and light trucks in the U.S. is 10.8 years. Assume that the standard deviation for this population is 3.7 years. A sample of 35 randomly selected vehicles was selected. What is the probability that the sample mean will be greater than 10 years?
Answers
Answer:
10.03% probability that the sample mean will be greater than 10 years
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question, we have that:
\(\mu = 10.8, \sigma = 3.7, n = 35, s = \frac{3.7}{\sqrt{35}} = 0.6254\)
What is the probability that the sample mean will be greater than 10 years?
This is 1 subtracted by the pvalue of Z when X = 10. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{10 - 10.8}{0.6254}\)
\(Z = -1.28\)
\(Z = -1.28\) has a pvalue of 0.1003
10.03% probability that the sample mean will be greater than 10 years
Find the general solution, in implicit form, to the differential equation dy/dx = 9 + 5x ^1/2 / 8+ (13y)^1/2 x>0, y>0Then, rearrange the solution that you get into the form f (x,y) = C, for some constant C.
Answers
A general solution is one which involves the integer 'n' and gives all solutions of a trigonometric equation.
What is general and particular solution of differential equation?A specific differential equation solution is one with the formula y = f(x), which lacks any arbitrary constants. The arbitrary constants a and b are used in the differential equation's general solution, which has the form y = f(x) or y = axe + b.The differential equation's solution can be quickly and easily found by integrating each variable once it has been separated. The formulas are: f(x)dx+g(y)dy=0, where f(x) and g(y) are respectively constants or functions of x and y.Any equation involving the unknown function y=f(x) and one or more of its derivatives is known as a differential equation. A function y=f(x) that satisfies the differential equation when f and its derivatives are replaced into the equation is a solution to a differential equation.Given data :
dy / dx = 9 + \(\frac{9 + (5x)^{1/2} }{8 + (13y)^{1/2} }\) ; x > 0
The general solution of a differential equation in implicit form is obtained as follows
dy / dx = h(x) / g(y)
g(y)dy = {8 + (13y)^{1/2}
h(x) dx = {9 + (5x)^{1/2}
F(x,y) = C
Learn more about differential equation refer to :
https://brainly.com/question/17004129
#SPJ4
The blueprint for a circular gazebo has a scale of 2 inches=5 feet. The blueprint shows that the gazebo has a diameter of 5.1 inches. What is the actual diameter of the gazebo? What is its area? Use 3.14 for π.
Answers
The actual diameter of the gazebo is 12.75 feet and has an area of
127.6 square inches.
What is a scale factor?The scale factor defines a variable in a ratio of two different measurements.
Sometimes drawings of large models are represented in a scale factor of a smaller unit.
Given, The blueprint for a circular gazebo has a scale of 2 inches = 5 feet.
So, The scale factor is (5/2) = 2.5 or 1 inch = 2.5 feet.
Also given, The gazebo has a diameter of 5.1 inches.
Therefore, The actual diameter of the gazebo is = 5.1×2.5 = 12.75 feet.
The area of the gazebo is π(12.75/2)² = 127.6 square inches.
learn more about scale factors here :
https://brainly.com/question/30215119
#SPJ1
Mrs Martin has $7000 in her saving account. Alonzo has 1/10 as much money in his account as Mrs Martin. How much money does Alonzo have in his account?
Answers
Answer:
7000*1/10
In a calculator type in 7000*(1/10)
700
Step-by-step explanation:
[-12] + [4] find the absolute value of each integer then add them
Answers
Hello there!
Answer:
16
Step-by-step explanation:
\( |x| = x \: \: \: if \: \: x \: \geqslant 0 \\ |x| = - x \: \: \: if \: \: \: x \: \leqslant 0\)
-12 < 0 so |-12| = -(-12) = 12
4 > 0 so |4| = 4
|-12| + |4| = 12 + 4 = 16
Answer:
16
Step-by-step explanation:
Hello! This question is looking for the absolute value of integers. The absolute value is the distance the number has from zero. For example, -12 as twelve numbers away from zero, twelve away in the negative direction. The absolute value of -12, then, is just twelve. An easy way to remember this is to take away the negative sign when taking the absolute value, since an absolute value can never be negative. The absolute value sign is represented by a squarish bracket [ and ].
This question says to find the absolute value of each integer and then add the two. First we have [-12]. This is 12 away from zero, and we can take away the - sign from the asked integer and we get 12.
The second integer given is 4, and when we take the absolute value of 4, [+4], we get positive four. This is because four is four spaces away from zero on the number line.
Thus, we have +12 and +4 as are values to add since they are the absolute values and we can form this equation
12+4=16
Thus, the answer is 16.
Hope this helps! Remember the hint, when something has brackets like that or asks for the absolute value, take away a negative sign and make it positive! Have a great day!
The height of a rectangular box is 7 ft. The length is 1 ft longer than thrice the width x. The volume is 798 ft³.
(a) Write an equation in terms of x that represents the given relationship.
The equation is
Answers
The equation in terms of x that represents the given relationship is 114 = (1 + 3x) * (Width)
Let's break down the information given:
Height of the rectangular box = 7 ft
Length of the rectangular box = 1 ft longer than thrice the width (x)
Volume of the rectangular box = 798 ft³
To write an equation that represents the given relationship, we need to relate the length, width, and height to the volume.
The volume of a rectangular box is given by the formula: Volume = Length * Width * Height.
Given that the height is 7 ft, we can substitute this value into the equation.
Volume = (Length) * (Width) * (7)
Now, let's focus on the length. It is described as 1 ft longer than thrice the width.
Length = 1 + (3x)
Substituting this value into the equation, we have:
Volume = (1 + (3x)) * (Width) * (7)
Since the volume is given as 798 ft³, we can set up the equation as follows:
798 = (1 + (3x)) * (Width) * 7
Simplifying further, we get:
798 = 7 * (1 + 3x) * (Width)
Dividing both sides of the equation by 7, we have:
114 = (1 + 3x) * (Width)
Therefore, the equation in terms of x that represents the given relationship is:
114 = (1 + 3x) * (Width)
For more question on equation visit:
https://brainly.com/question/17145398
#SPJ8
A student is taking a history course and an English course. He decides that the probability of passing the history course is .75 and the probability of passing the English course is .84. If these events are independent, what is the probability that (a) he passes both courses; (b) he passes exactly one of them
Answers
Answer:
a. 0.63
b. 0.33
Step-by-step explanation:
Here is a probability question. When two events are independent, it means that the probability of one of the events happening has no effect on the probability on the other happening.
From the question, let P(H) be the probability of passing the history course while P(E) is the probability of passing the English course;
By representation;
P(H) = 0.75
P(E) = 0.84
a) Probability of passing both
This means that he passes history and also passes English;
Mathematically that would be represented as;
P(E) * P(H) = 0.84 * 0.75 = 0.63
b) Probability that he passes exactly one of the courses.
This means that he passes one and he fails the other. Mathematically, we should remember that the probability of an event not happening = 1 - probability of the event happening
Let P’(H) and P’(E) be the probability of failing the history and english courses respectively;
Thus; P’(H) = 1 - 0.75 = 0.25
while P’(E) = 1-0.84 = 0.16
Now the probability that he passes exactly one means he passes one and fails the other.
So in this case, we have two scenarios; He passes History and fail English or passes English and fails history.
Thus, we have;
[P(H) and P’(E) or P(E) and P’(H)]
In probability, and means multiplication while or means addition; thus we have;
{P(H) * P’(E) } + {P’(H) * P(E)}
= ( 0.75 * 0.16) + (0.25 * 0.84)
= 0.12 + 0.21 = 0.33
Is this correct or not?
If not please provide correct answer

Answers
Answer:
It is correct please I do not want yo sound rude can you give me brainliest answer.
Answer:
correct steps
Step-by-step explanation:
if asked to find angles in terms of the ratios, then don't forget to shift sin / cos / tan across the equal sign and change it to arc sin / cos / tan.
Name the property illustrated If g = 3h and 3h = 16, then g = 16
3
Answers
The property illustrated ca be classified as the transitive property of equality
Transitive property of equalityEquation are expressions separated by an equal sign. For transitive property, if two system of equation are equal, and the first is equal to the second, then they 2nd is equal to the third, they are transitive.
According to the transitive property of equality, two quantities that are equal to the same thing are equal to each other. For instance If x = 10 and 10 = y, then x = y.
Given that g = 3h and 3h = 16, then g = 16, then the property illustrated ca be classified as the transitive property of equality
Learn more on transitive property here: https://brainly.com/question/4083674
#SPJ1
Determine the probability of rolling a die and getting a 2
then a 5.
Answers
The probability of rolling a die and getting a 2, then a 5, is 1/36.
To determine the probability of rolling a die and getting a 2, then a 5, we need to multiply the probabilities of each event happening.
First, let's consider the probability of rolling a die and getting a 2. Since there are six equally likely outcomes when rolling a fair six-sided die (numbers 1 to 6), the probability of rolling a 2 is 1/6.
Now, let's consider the probability of rolling a die and getting a 5. Again, there are six equally likely outcomes, so the probability of rolling a 5 is also 1/6.
To find the probability of both events happening, we multiply the probabilities:
Probability of rolling a 2 and then a 5 = (1/6) * (1/6) = 1/36.
Therefore, the probability of rolling a die and getting a 2, then a 5, is 1/36.
It's important to note that each roll of the die is an independent event, meaning that the outcome of one roll does not affect the outcome of the next roll. Therefore, the probability of rolling a 2 and then a 5 remains constant at 1/36 regardless of previous rolls or the order in which they occur.
For more such questions on probability visit:
https://brainly.com/question/251701
#SPJ8
Please solve this ASAP!!! :)

Answers
Answer:
1). Area = 37 cm²
2). Area = 120 cm²
Step-by-step explanation:
Figures in the picture attached are the examples of composite figures.
1). Area of the composite figure = Area of rectangle A + Area of rectangle B
Since area of rectangle = Length × width
Area of rectangle A = 8 × 2 = 16 cm²
Area of rectangle B = 3 × 7 = 21 cm²
Area of the composite figure = 16 + 21 = 37 cm²
2). Area of the composite figure = Area of C + Area of D
= (3×4) + (9×12)
= 12 + 108
= 120 cm²
The table shows a linear function.
Which equation represents the function?
x f(x)
-6 -1
-3 4
0 9
3 14
A. f(x)= -5/3x+9
B. f(x)= -5/3x-9
C. f(x)= 9x+5/3
D. f(x)= 5/3x+9
Answers
Answer:
D.
Step-by-step explanation:
Try A:
x = -6, f(x) = -1:-
f(-6) = -5/3(-6) + 9
= 10 + 9 = 19 NOT A.
Try B:
f(-3) = -5/3(-3) - 9
= 5 - 9 = -4 NOT B
Try C:
9(0) + 5/3 = 5/4 NOT C
Try D:
f(3) = 5 + 9 = 14
f(0) = 9, f(-6) = -1 and f(-3) = 4
PLEASE HELP NOW
HURRY

Answers
Answer:
13
Step-by-step explanation:
we us the pythagorean theorem
sqrt( 144 + 25) = 13
-4(6x + 7) = -316 What is the answer?
Answers
Answer:
\(x=-\frac{43}{3}\)
Step-by-step explanation:
\(-4(6x+7)=-316 \\ \\ 6x+7=-79 \\ \\ 6x=-86 \\ \\ x=-\frac{43}{3}\)
Answer:
x=12
Step-by-step explanation:
hope this helps! -4(6x + 7) = -316=x=12

URGENT!! ILL GIVE
BRAINLIEST!!!! AND 100 POINTS!!!!!

Answers
11x+4x=180
15x=180
x=12
house designer uses computer-aided drawings to illustrate new houses. She likes to show her drawings to clients on a large screen. She often uses the zoom-in function to enlarge the drawings so that clients can see certain features better.
Each click of the zoom-in button results in a 10 percent increase in the size of a drawing.
(a) On a certain drawing of a house, the width of the front door is 3 inches on screen, using the default settings. Make a table of values to show the width of the door on screen after each of the first four clicks of the zoom-in button. These values should be accurate to the thousandths place.
(b) Write an algebraic rule for the function that will give the display size of the door for any number of clicks.
c) To show clients a detail on the front door, she needs to zoom in so the door is approximately 3 feet wide on screen. How many clicks of the zoom-in button will be needed to make this enlargement? Explain how you got your answer.
d) Suppose one click of the zoom-out button results in a 10 percent decrease in the size of the drawing. How many clicks of the zoom-out button would it take to transform the display of the door from 3 feet wide back to a width of approximately 3 inches?
Explain how you got your answer.


Answers
(a) Clicks Width of Door (inches)
1 3.3
2 3.63
3 3.99
4 4.39
(b) The function is y = 3 (1.1)ˣ.
(c) It would take about 15 clicks of the zoom-in button to make the door approximately 3 feet wide on the screen.
(d) It would take about 12 clicks of the zoom-out button to transform the display of the door from 3 feet wide back to a width of approximately 3 inches.
(a)
Clicks Width of Door (inches)
1 3.3
2 3.63
3 3.99
4 4.39
(b) Let x be the number of clicks and y be the width of the door on the screen. Then, we can write the algebraic rule as:
y = 3 (1.1)ˣ
(c) To make the door approximately 3 feet wide on screen, we need to convert 3 feet to inches, which is 36 inches. Then, we need to solve for x in the equation:
3 (1.1)ˣ = 36
Dividing both sides by 3, we get:
(1.1)ˣ = 12
Taking the logarithm of both sides (with base 1.1), we get:
x = log(12) / log(1.1) ≈ 14.7
So, it would take about 15 clicks of the zoom-in button to make the door approximately 3 feet wide on the screen.
(d) To transform the display of the door from 3 feet wide back to a width of approximately 3 inches, we need to find the number of clicks of the zoom-out button that will result in a width of approximately 3 inches. We can use the same formula as before, but with the initial width of 36 inches (since we are zooming out):
36 (0.9)ˣ = 3
Dividing both sides by 36, we get:
(0.9)ˣ = 1/12
Taking the logarithm of both sides (with base 0.9), we get:
x = log(1/12) / log(0.9) ≈ 11.5
So, it would take about 12 clicks of the zoom-out button to transform the display of the door from 3 feet wide back to a width of approximately 3 inches.
To learn more about the exponential function;
https://brainly.com/question/14344314
#SPJ1
Question 2 of 10
Which value of x is in the domain of f(x)=√x-11?
O A. x= 13
OB. x= 10
OC. x= -4
OD. X=0
Answers
The value of x in the domain of function f(x) = √(x - 11) will be 13. Then the correct option is A.
What is a function?A function is an assertion, concept, or principle that establishes an association between two variables. Functions may be found throughout mathematics and are essential for the development of significant links.
The domain means all the possible values of x and the range means all the possible values of y.
The function is given below.
f(x) = √(x - 11)
The value inside the square root should be greater than or equal to zero. Then we have
x - 11 ≥ 0
x ≥ 11
The value of x in the domain of function f(x) = √(x - 11) will be 13. Then the correct option is A.
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ9
Any help with this? It's a proof, but not a long one

Answers
KL is congruent to JM (given)
Angle N is congruent to angle N (reflexive)
Triangle JNM is congruent to triangle KNL (AAS)
LN is congruent to MN (CPCTC)