Answers
\(\huge\fbox\pink{Answer}\)
6.) ∆DAY
7.) SAS
Reason:- SN corresponds to DY UN corresponds to AYhence, ∆SUN is congruent to ∆DAY
SN = DY UN = AY<N = <Yhence, both the triangles are congruent due to SAS
I hope this helps
Related Questions
Please help! I am timed here. I am not sure about this question.

Answers
Answer:
it would be -12
Step-by-step explanation:
Find the volume of a square pyramid if the area of the base is 441 ft2 and the height is 24 ft.? Round to the nearest tenth.
Answers
Answer:
440
Step-by-step explanation:
Use the definition of Taylor series to find the Taylor series (centered at c) for the function. Use the definition of Taylor series to find the Taylor series (centered at c) for the function. f(x) = cos x, c = pi/4 f(x) = sigma^infinity_n = 0 Use the definition of Taylor series to find the Taylor series (centered at c) for the function. Use the definition of Taylor series to find the Taylor series (centered at c) for the function. f(x) = ln(x), c = 1 f(x) = sigma^infinity_n = 0 Find the Maclaurin series for the function. (Use the table of power series for elementary functions.) Find the Maclaurin series for the function. (Use the table of power series for elementary functions.) f(x) = ln (1 + x^9) f(x) = sigma^infinity_n = 1
Previous question
Answers
1. The Taylor series for f(x) = cos(x) centered at c = π/4 is:
f(x) = cos(π/4) - sin(π/4)(x - π/4) + (1/2)cos(π/4)(x - π/4)^2 - (1/6)sin(π/4)(x - π/4)^3 + ...
2. The Taylor series for f(x) = ln(x) centered at c = 1 is:
f(x) = ln(1) + (x - 1) - (x - 1)^2/2 + (x - 1)^3/3 - ...
3. The Maclaurin series for f(x) = ln(1 + x^9) is:
f(x) = x^9 - (1/2)x^18 + (1/3)x^27 - ...
1. The Taylor series expansion for cos(x) centered at c is derived by using the derivatives of the function evaluated at c. The general form of the series includes terms with alternating signs and higher powers of (x - c).
2. Similarly, the Taylor series expansion for ln(x) centered at c is obtained by finding the derivatives of the function and evaluating them at c. The resulting series includes powers of (x - c) with coefficients derived from the derivatives.
3. For the Maclaurin series, we center the Taylor series at c = 0. In the case of f(x) = ln(1 + x^9), we use the power series expansion of ln(1 + x) and substitute x^9 in place of x. The resulting series includes terms with positive powers of x^9 and coefficients determined by the power series for ln(1 + x).
To know more about series refer here:
https://brainly.com/question/32235538#
#SPJ11
Simplify the following expression by combining liker terms: 4x +9 -6x +6
10X-15
10x+15
-2x+15
2x+15
Explain your thinking.
Answers
Answer:
its very simple you just need to collect like terms...
which is 4x-6x+6+9 which is
-2x+15.
This is my answer I hope it helps you.
Answer:
i think its -2x+15
Step-by-step explanation:
you do 4x-6x (-6 cuz it has a neg. in front) which gives you -2x then 9+6 and it gives you 15
Evaluate f(g(0)) when
f(x) = x-3 and g(x) = -x^2 - 4x
Answers
Answer:
-3
Step-by-step explanation:
g(0) = 0
f(g(0)) = 0 - 3 = -3
What are 2 digit multiples of 27?
Answers
The first 20 multiples of 27 are as follows:
27, 54, 81, 108, 135, 162, 189, 216, 243, 270, 297, 324, 351, 378, 405, 432, 459, 486, 513, and 540.
What are multiples?A multiple in mathematics is created by multiplying any number by an integer.
In other words, if b = na for some integer n, known as the multiplier, it can be said that b is a multiple of a given two numbers, a and b.
This is equivalent to stating that b/a is an integer if an is not zero.
A is known as a divisor of b when a and b are both integers and b is a multiple of a.
First 20 multiples of 27:
27, 54, 81, 108, 135, 162, 189, 216, 243, 270, 297, 324, 351, 378, 405, 432, 459, 486, 513, and 540.
Therefore, the first 20 multiples of 27 are as follows:
27, 54, 81, 108, 135, 162, 189, 216, 243, 270, 297, 324, 351, 378, 405, 432, 459, 486, 513, and 540.
Know more about multiples here:
https://brainly.com/question/26856218
#SPJ4
Correct question:
What are the first 20 multiples of 27?
m=3 through (-1,-4) ............ (slope intercept equation)
Answers
Answer:
y=3x-1
Step-by-step explanation:
Fred has 155 orange balloons Fred has 31 times more orange balloons than Dan how many orange balloons does Dan have?
Answers
Answer:
5
Step-by-step explanation:
since Fred has 31 times more balloons then Dan, and Fred has 155, 155/31=5
Finding equations of exponential function

Answers
The exponential function are y = 10(2)^x, y = 1.270(1.389)^x, y = 5.656(0.957)^x and y = 6.567(0.870)^x.
What is the equation of the exponential function1. (a) To find the equation of the exponential function that passes through the points (0,10) and (3,80), we can use the formula:
y = a(b)^x
where a and b are constants that we need to find.
First, we can use the point (0,10) to solve for a:
10 = a(b)^0
10 = a
Next, we can use the point (3,80) to solve for b:
80 = 10(b)^3
8 = b^3
b = 2
Therefore, the equation of the exponential function is:
y = 10(2)^x
(b) To find the equation of the exponential function that passes through the points (0.18, 2.8) and (2, 8), we can use the same formula:
y = a(b)^x
First, we can use the point (0.18, 2.8) to solve for a:
2.8 = a(b)^0.18
Next, we can use the point (2, 8) to solve for b:
8 = a(b)^2
Dividing the second equation by the first, we get:
2.857 = (b)^1.82
b = 1.389
Substituting this value of b back into one of the equations to solve for a, we get:
2.8 = a(1.389)^0.18
a = 1.270
Therefore, the equation of the exponential function is:
y = 1.270(1.389)^x
2. (a) To find the equation of the exponential function that passes through the points (2, 5.12288) and (1.92, 2.192), we can again use the formula:
y = a(b)^x
First, we can use the point (2,5.12288) to solve for a:
5.12288 = a(b)^2
Next, we can use the point (1.92,2.192) to solve for b:
2.192 = a(b)^1.92
Dividing the second equation by the first, we get:
0.427 = (b)^(0.08)
b = 0.957
Substituting this value of b back into one of the equations to solve for a, we get:
5.12288 = a(0.957)^2
a = 5.656
Therefore, the equation of the exponential function is:
y = 5.656(0.957)^x
(b) To find the equation of the exponential function that passes through the points (1.192,5) and (5,0.75), we can use the same formula:
y = a(b)^x
First, we can use the point (1.192,5) to solve for a:
5 = a(b)^1.192
Next, we can use the point (5,0.75) to solve for b:
0.75 = a(b)^5
Dividing the second equation by the first, we get:
0.149 = (b)^3.808
b = 0.870
Substituting this value of b back into one of the equations to solve for a, we get:
5 = a(0.870)^1.192
a = 6.567
Therefore, the equation of the exponential function is:
y = 6.567(0.870)^x
3. To find the equation of the exponential function that passes through the points (2.14,7) and (7,205), we can use the same formula as before:
y = a(b)^x
First, we can use the point (2.14,7) to solve for a:
7 = a(b)^2.14
Next, we can use the point (7,205) to solve for b:
205 = a(b)^7
Dividing the second equation by the first, we get:
29.285 = (b)^(4.86)
b = 5.474
Substituting this value of b back into one of the equations to solve for a, we get:
7 = a(5.474)^2.14
a = 0.00061
Therefore, the equation of the exponential function is:
y = 0.00061(5.474)^x
Rounding a and b to the nearest hundred, we get:
a = 0.0006
b = 5.47
So, the final equation of the exponential function is:
y = 0.0006(5.47)^x
We can check if the points (2.14,7) and (7,205) fall on the curve by plugging them into the equation:
y = 0.0006(5.47)^x
When x = 2.14:
y = 0.0006(5.47)^2.14 ≈ 7
When x = 7:
y = 0.0006(5.47)^7 ≈ 205
So, the points do fall on the curve, which means that the equation we found is correct.
Learn more on exponential function here;
https://brainly.com/question/2456547
#SPJ1
epidemiologic studies are of significant value to scientists who use the information from these studies to formulate dose-response estimates to predict the risk of:
Answers
Epidemiologic studies are of significant value to scientists who use the information from these studies to formulate dose-response estimates to predict the risk of various health outcomes or diseases.
By analyzing data on exposure levels and corresponding health effects in a population, researchers can establish the relationship between the dose (amount of exposure) and the response (risk or occurrence of the outcome). This allows them to estimate the potential risks associated with different levels of exposure to specific factors such as environmental pollutants, medications, lifestyle choices, or occupational hazards. These dose-response estimates help inform public health interventions, risk assessments, and policy-making decisions aimed at minimizing the occurrence and impact of health risks in populations.
To know more about Epidemiologic studies,
https://brainly.com/question/31319245
#SPJ11
P is inversely proportional to q^3, when p has the value 27, q has the value 3. i) find the formula which expresses p in terms of q. P= r is directly proportional to q, when r has the value 10, q has the value 2. ii) prove that r=kp^n and so find the value of k and n.
Answers
Answer:
Step-by-step explanation:
i) If p is inversely proportional to q³, this is expressed as p ∝ q³
p = k/q³ where q is the proportionality constant.
Given p = 27 and q = 3
Substitute this values into the formula
27 = k/(3)³
27 = k/27
k = 27×27
k = 729
Substitute k = 1 into the formula
p = 729/(q)³
Hence the formula which expresses p in terms of q is p = 729/q³
ii) If r is directly proportional to q, it is expressed as r ∝ q
r = kq
If r = 10 and q = 2
Substitute
10 = 2k
k = 10/2
k = 5
The equation becomes
r = 5q... 1
From 1) p = 729/q³
q³ = 729/p
q = 9/³√p
q = 9/p^1/3....2
Substitute equation 2 into 1
r = 5(9/p^1/3)
r = 45p^-1/3
Compare r = 45p^-1/3 with r = kp^n
k = 45 and n = -1/3
Find the perimeter of the triangle XYZ with verticles X (1, 3) , Y(-4, -1) and Z(4, -1). Round your answer to two decimal places
Answers
Answer:
The perimeter is approximately 6.40.
Step-by-step explanation:
To find the perimeter of a triangle with vertices X (1, 3), Y (-4, -1), and Z (4, -1), we can first find the distance between each pair of points using the distance formula.The distance between points X and Y is:
$d(X,Y) = \sqrt{((1 - (-4))^2 + (3 - (-1))^2)} = \sqrt{25 + 16} = \sqrt{41}$
The distance between points Y and Z is:$d(Y,Z) =
\sqrt{((-4 - 4)^2 + ((-1) - (-1))^2)} = \sqrt{0 + 0} = 0$
The distance between points X and Z is:
$d(X,Z) = \sqrt{((1 - 4)^2 + (3 - (-1))^2)} = \sqrt{9 + 16} = \sqrt{25}$
We can then find the perimeter of the triangle by adding up the lengths of the sides. In this case, the perimeter is $d(X,Y) + d(Y,Z) + d(X,Z) = \sqrt{41} + 0 + \sqrt{25} = \sqrt{41} + \sqrt{25} = 6.40\ldots$.
Rounded to two decimal places, the perimeter is approximately 6.40.
what equation has the same solution as x^2-16x+20=-2
Answers
The equation that has the same solution as x² - 16x + 20 = -2 is x² - 16x + 22 = 0.
How did we arrive at this assertion?To find an equation with the same solution as the equation x² - 16x + 20 = -2, manipulate the given equation while preserving its solutions.
Starting with the given equation:
x² - 16x + 20 = -2
Move the constant term (-2) to the other side:
x² - 16x + 20 + 2 = 0
Simplifying:
x^2 - 16x + 22 = 0
Therefore, the equation that has the same solution as x² - 16x + 20 = -2 is x² - 16x + 22 = 0.
learn more about equation: https://brainly.com/question/22688504
#SPJ1
What is the answer for C = π/2
Answers
Answer:
C=5π/2
Step-by-step explanation:
Can you find the slope and type the correct code? Please remember to type in ALL CAPS with no spaces.
Answers
Yes, I can find the slope of a line and type the correct code. The SLOPE function will return the slope of the linear regression line that best fits the data.
The slope of a line is the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. The formula for finding the slope of a line is (y2 - y1)/(x2 - x1), where (x1, y1) and (x2, y2) are any two points on the line.
The slope is a measure of how steep the line is. It can be positive, negative, zero, or undefined. The code for finding the slope of a line in ALL CAPS with no spaces is SLOPE.
To use this function in Excel, you need to provide the range of x-values and the range of y-values.
To learn more about : slope
https://brainly.com/question/16949303
#SPJ11
Choose Yes or No to tell whether or not the symbol needs to flip when completing this inequality:
- 6w < 21
Answers
Answer:
yes ..................
1. A dog food company is interested in how much dog food a dog consumes based off of its weight. The company takes a random sample of dogs and finds that the best regression model to represent the data is as follows:Simple Linear Regression Results:Dependent Variable: Ounces of Food Consumed in a WeekIndependent Variable: WeightFood Consumed=−32.86+5.25×WeightSample Size: 500R2: 0.8129Estimate of error standard deviation: 7.8563121Suppose that a dog weighs 42.4 pounds, and typically eats 180 ounces of food per week. How many ounces of food would we predict the dog eats in a week, based on the least squares estimate? Provide your answer accurate to 1 digit past the decimal point.2. Suppose another dog weighs 24.7 pounds and consumes 70 ounces of food per week. What is the residual associate to this individual using the least squares estimate? Provide your answer accurate to 1 digit past the decimal point.
Answers
The residual associated with this individual is approximately -15.4 ounces, using the least squares estimate. This means that the actual amount of food consumed is about 15.4
We would predict that the dog would eat approximately 180.96 ounces of food in a week, based on the least squares estimate. the residual associated with this individual is approximately -15.4 ounces, using the least squares estimate. This means that the actual amount of food consumed is about 15.4 ounces less than what would be predicted based on the regression model.
Using the given regression model, we can estimate the amount of food a dog weighing 42.4 pounds would consume in a week as:
Food Consumed = -32.86 + 5.25 × Weight
Food Consumed = -32.86 + 5.25 × 42.4
Food Consumed ≈ 180.96 ounces
Therefore, we would predict that the dog would eat approximately 180.96 ounces of food in a week, based on the least squares estimate.
To find the residual associated with a dog weighing 24.7 pounds and consuming 70 ounces of food per week, we first need to calculate the predicted value of food consumed based on the given regression model:
Food Consumed = -32.86 + 5.25 × Weight
Food Consumed = -32.86 + 5.25 × 24.7
Food Consumed ≈ 85.38 ounces
The residual is then calculated as the difference between the actual value of food consumed (70 ounces) and the predicted value (85.38 ounces):
Residual = Actual Value - Predicted Value
Residual = 70 - 85.38
Residual ≈ -15.4 ounces
Therefore, the residual associated with this individual is approximately -15.4 ounces, using the least squares estimate. This means that the actual amount of food consumed is about 15.4 ounces less than what would be predicted based on the regression model.
Learn more about regression model
https://brainly.com/question/14983410
#SPJ4
Which shows how to multiply 2/5×4?
Responses
2×5÷4 you will be rewarded 10 points
2 times 5 divided by 4
2×4÷5
2 times 4 divided by 5
8×2÷5
8 times 2 divided by 5
4×5÷2
Answers
Answer:
i believe this is how you solve that problem... 2÷5×4
A local charity has put together 20 care packages for
people. Each package contains $15 worth of goodies
and $2.50 per food satchel added to it. If the charity
spent $800 on the care packages how many food
satchels were in each package? Write and solve an
equation for this scenario.
Answers
Answer:
The equation is 15x + 2.50y = 800, where x is the number of care packages and y is the number of food satchels. Solving for y, we get y = 32. Therefore, each package contained 32 food satchels.
Step-by-step explanation:
Find the derivative of the function. \[ h(t)=(t+4)^{2 / 3}\left(2 t^{2}-3\right)^{3} \]
Answers
Therefore, the derivative of h(t) is \(h'(t) = (4t2 - 6)(t + 4)-1/3(2t2 - 3)3 + 12t(t + 4)2/3(2t2 - 3)2.\)
We have to determine the derivative of the given function:
\(h(t) = (t + 4)2/3 (2t2 - 3)3\).
Using the product rule, we can find the derivative of h(t) as follows
\(h(t) = (t + 4)2/3 (2t2 - 3)3h'(t) = [(t + 4)2/3 (2t2 - 3)3]'h'(t) = [(t + 4)2/3]'(2t2 - 3)3 + (t + 4)2/3(3)(2t2 - 3)2(4t)h'(t) = [(2/3)(t + 4)-1/3](2t2 - 3)3 + (t + 4)2/3(3)(2t2 - 3)2(4t)h'(t) = [(2/3)(2t2 - 3)](t + 4)-1/3(2t2 - 3)3 + 12t(t + 4)2/3(2t2 - 3)2h'(t) = (4t2 - 6)(t + 4)-1/3(2t2 - 3)3 + 12t(t + 4)2/3(2t2 - 3)2\)Therefore, the derivative of h(t) is \(h'(t) = (4t2 - 6)(t + 4)-1/3(2t2 - 3)3 + 12t(t + 4)2/3(2t2 - 3)2.\)
To know more about derivative visit:
https://brainly.com/question/29144258
#SPJ11
Solve: -3+ h = 40
HELPPP

Answers
Answer:
answer: c, 43
Step-by-step explanation:
-3+h=40
+3 +3 add 3 to both sides
h=43
Answer:
Its c
Step-by-step explanation:-3 + h = 40 cause 43 -3 is 40
find the volume of the solid

Answers
V=5✖️3✖️6➕5✖️3✖️5➕5✖️3✖️3=210
Two sisters like to compete on their bike rides. Kristen can go 8 mph faster than her sister, Emily. If it takes Emily one hour longer than Kristen to go 58.5 miles, how fast can Emily ride her bike
Answers
Emily can ride her bike at a speed of 65 mph.
Let's use "x" to represent Emily's speed in mph.
We know that Kristen's speed is 8 mph faster, so her speed would be x + 8 mph.
We also know that Emily takes one hour longer than Kristen to travel 58.5 miles. So we can set up an equation:
\(\frac{58.5}{x} = \frac{58.5}{x+8} +1\)
This equation represents the fact that the time it takes for Emily to travel 58.5 miles is one hour more than the time it takes for Kristen to travel the same distance.
Now, let's solve for x:
Multiplying both sides by x(x+8), we get:
\(58.5(x+8) = 58.5x + x(x+8)\)
\(58.5x + 468 = 58.5x + x^2 + 8x\)
Simplifying, we get:
\(x^2 + 8x - 468 = 0\)
Now we can use the quadratic formula:
\(x = \frac{(-8 ± \sqrt{8^{2} - 4(1)(-468) }}{2(1)}\)
\(x = \frac{(-8±\sqrt{18976)}}{2}\)
\(x = \frac{(-8±132)}{2}\)
x = -73 or x = 65
Since Emily's speed can't be negative, we can discard the negative solution. Therefore, Emily can ride her bike at a speed of 65 mph.
To know more about "Quadratic formula" refer here:
https://brainly.com/question/22364785#
#SPJ11
Mary lou received $14,000 from her grandparents for her college education 7 years prior to her enrolling in college. mary lou invested the money at 5.5% compounded semiannually. how much money will she have in her savings account when she is ready to enroll in college?
Answers
Mary lou will have $20574.6 in her savings account when she is ready to enroll in college.
For given question,
Mary lou received $14,000, 7 years prior to her enrolling in college.
She invested the money at 5.5% compounded semiannually.
so the Principal(P) = $14000
Rate (R) = 5.5%
Period(t) = 7 years
First we find the rate of interest in decimal form.
5.5% = 5.5/100
5.5% = 0.055
so, r = 0.055
Using the formula for continuous compound interest,
\(\Rightarrow A = Pe^{rt}\\\\\Rightarrow A=14000\times e^{(0.055\times 7)}\)
⇒ A = 14000 × e^(0.385)
⇒ A = 14000 × 1.4696
⇒ A = $20574.6
This means, after 7 years she will have $20574.6 in her saving account.
Therefore, Mary lou will have $20574.6 in her savings account when she is ready to enroll in college.
Learn more about continuous interest here:
https://brainly.com/question/14295570
#SPJ4
match each equation to an equivalent equation written in slope intercept form

Answers
Answer:
2x+y=3 --> y= -2x+3
2y-6=x --> y= 1/2x+3
x-3y=-6 --> y= 1/3x+2
-x+1/2y=3 --> y= 2x+6
Step-by-step explanation:
i hope this helps :)
The solution to the system of equations is
2x + y = 3 ; y = -2x + 3
2y - 6 = x ; y = ( 1/2 )x + 3
x - 3y = -6 ; y = ( 1/3 )x + 2
-x + ( 1/2 )y = 3 ; y = 2x + 6
What is an Equation of a line?The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation be represented as A
Now , the value of A is
a)
Let the equation be 2x + y = 3
Subtracting 2x on both sides of the equation , we get
y = 3 - 2x
So , the equation in slope intercept form is y = 3 - 2x
b)
Let the equation be 2y - 6 = x
Adding 6 on both sides of the equation , we get
2y = x + 6
Divide by 2 on both sides of the equation , we get
y = ( 1/2 )x + 3
So , the equation in slope intercept form is y = ( 1/2 )x + 3
c)
Let the equation be x - 3y = -6
Adding 3y on both sides of the equation , we get
x = 3y - 6
Adding 6 on both sides of the equation , we get
3y = x + 6
Divide by 3 on both sides of the equation , we get
y = ( 1/3 )x + 2
So , the equation in slope intercept form is y = ( 1/3 )x + 2
d)
Let the equation be -x + ( 1/2 )y = 3
Adding x on both sides of the equation , we get
( 1/2 )y = 3 + x
Multiply by 2 on both sides of the equation , we get
y = 2x + 6
So , the equation in slope intercept form is y = 2x + 6
Hence , the equations are solved
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ2
Which table(s) can represent values of a function? Select all that apply
Answers
The tables that can represent values of a function are Table 1, Table 2, Table 4, and Table 5. These tables show a unique output value for each input value, which is the characteristic of a function
A function is a relation that assigns a unique output value to every input value. In Tables 1, 2, 3, and 4, there is a unique output value for each input value, which makes them all represent values of a function. In Table 5, however, there are repeated output values for different input values, which violates the definition of a function. Therefore, Table 5 does not represent values of a function.
Learn more about mathematics here: brainly.com/question/24600056
#SPJ4

given f(x)=2/3x-x^2 fine f(-3)
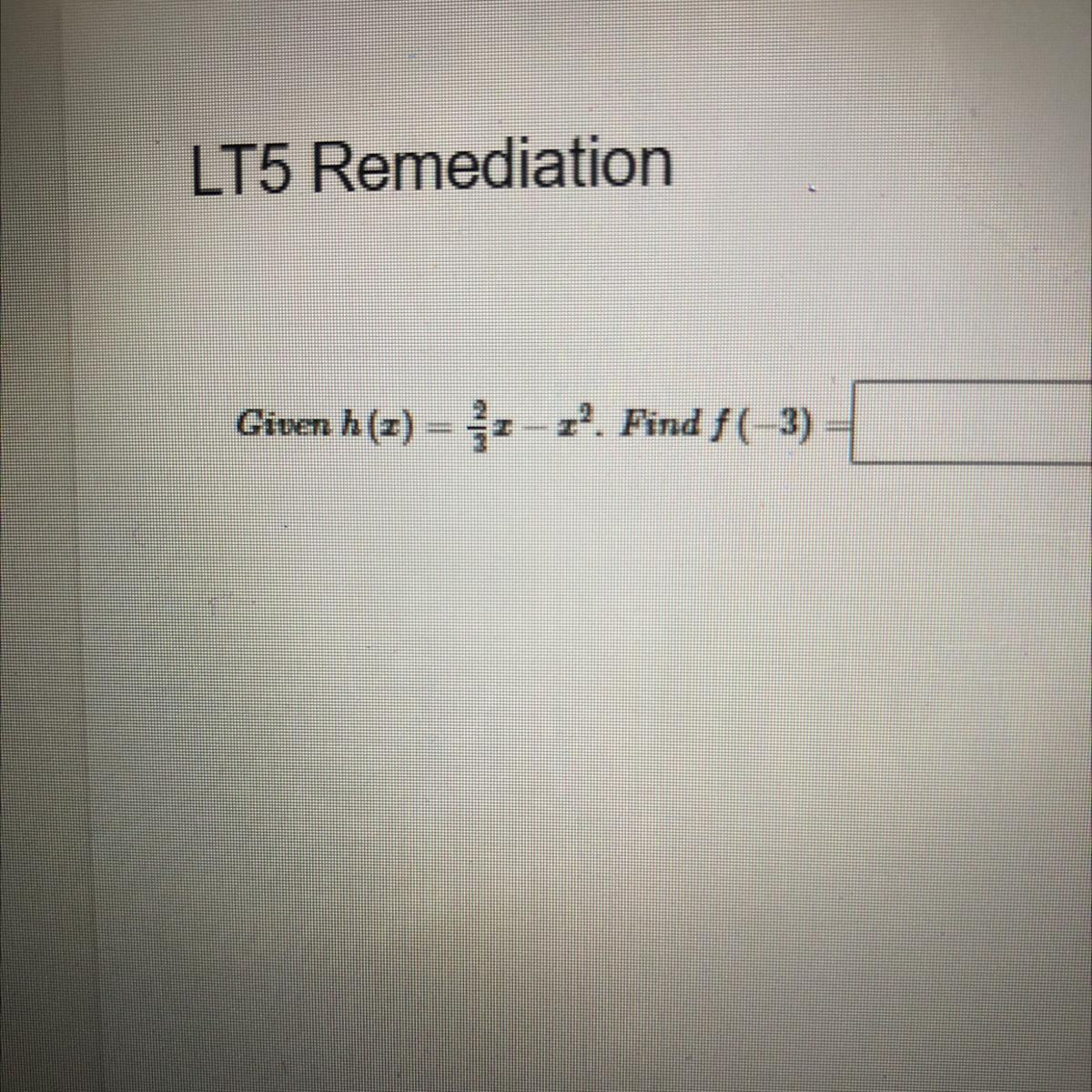
Answers
Answer:-4.5
Step-by-step explanation:
If u mind helping me some more it will be great thank u katie19

Answers
Less than <
Greater than >
Greater than >
-1/7,-1/2,-2/5,-3/10,-1/10
-2 2/3, -2, -1 2/3,
-1 1/3, -2/3
BRAINLIEST!!!! PLZZZZ SEE BELOW!!!

Answers
Answer:
b. 0.25
Step-by-step explanation:
40 + 120 = 160
40 / 160
answerrrrrr plssss ill giveee brainliesttttt

Answers
\(m\angle E=\sin \dfrac{\sqrt{10}}{2\sqrt5}=\sin \dfrac{\sqrt2}{2}=45^{\circ}\)
