I have 1 bag of marbles. I put in 3 extra marbles. There are now 9 marbles in the bag. How many were in the bag to begin with?
Please give me the formula and all too
Answers
Answer:
6 Marbles
Step-by-step explanation:
9-3=6
The bag of marbles had 6 marbles in it originally.
Answer:
6
x+3=9
Step-by-step explanation:
Related Questions
cual es el valor de "x" en la siguiente operación? 2x+1=11
Answers
Answer:
Subtract
1
1
1
from both sides of the equation
2
+
1
=
1
1
2
+
1
−
1
=
1
1
−
1
2
Simplify
3
Divide both sides of the equation by the same term
4
Simplify
Solution
=
5
Step-by-step explanation:
Answer:
5
Step-by-step explanation:
tienes que quitar 1 de 1 y 11 y te quedas con 10, despues divides 10 con 2x y tienes 5.
THIS IS 7TH GRADE MATH SO ITS EASY

Answers
Answer:
b
Step-by-step explanation:
Given: - 1/2 x > 6.
Choose the solution set.
{x | x R, x > -12}
{x | x R, x > -3}
{x | x R, x < -3}
{x | x R, x < -12}
Answers
Answer:
\(x > - 12\)
Step-by-step explanation:
\( - \frac{1}{2} x > 6 \\ \frac{ - \frac{1}{2} }{ - \frac{1}{2} } x > \frac{6} { - (\frac{ 1}{2} )} \\ x > 6 \times - \frac{2}{1}\)
Therefore:
\(x > - 12\)
You spin each spinner and find the sum. How many different sums are possible?
these are the spinners:

Answers
The different sums are possible are 18.
As, the number of different sums possible is given by the equation:
Number of different sums = n x m
In other words, we multiply the number of outcomes for the first spinner by the number of outcomes for the second spinner to get the total number of unique sums.
So, the different sums are possible
= 2 x 3 x 3
= 18
Learn more about outcome here:
https://brainly.com/question/32037007
#SPJ1
True or False: The height is always twice the length of tue base edge of any triangular pyramid.
Answers
Answer:
true
Step-by-step explanation:
3n3n3p0mdo98rueu33
Which of the following does NOT have a unit price of $24 for one sweater?
$38 for 2 sweaters
$72 for 3 sweaters
$96 for 4 sweaters
$120 for 5 sweaters
Answers
Answer:
$38 for 2 sweaters
Step-by-step explanation:
Every price for all other sweater options are divisible by 24, since it is the unit price (meaning 1 sweater = $24). 38 is not divisible by 24, but by 19. This means it does not follow the unit price. It would be a special sale.
Last week, Leah worked h
hours mowing lawns. She worked 5
hours more walking dogs than mowing lawns. She earned the same amount of money per hour for each job. The expression 24h+60
represents the total amount of money she earned last week. Enter a number in each box to create an equivalent expression which shows the amount of money she earned per hour.
Answers
The amount earned per an hour is -5/2.
What is Expression?An expression is combination of variables, numbers and operators.
Given that , Leah worked h hours mowing lawns.
Leah worked 5 hours more walking dogs than mowing lawns
Leah earned the same amount of money per hour for each job. The expression 24h+60 represents the total amount of money she earned last week.
We have to find the amount earned per an hour.
24h=-60
Divide both sides by 24
h=-5/2
Hence, the amount earned per an hour is -5/2.
To learn more on Expressions click:
https://brainly.com/question/14083225
#SPJ1
4x^2=x+3
Solve by factoring
Show your work please!
Answers
Answer:
x = - \(\frac{3}{4}\) , x = 1
Step-by-step explanation:
4x² = x + 3 ← subtract x + 3 from both sides
4x² - x - 3 = 0 ← in standard form
consider the factors of the product of the coefficient of the x² term and the constant term which sum to give the coefficient of the x- term.
product = 4 × - 3 = - 12 and sum = - 1
the factors are - 4 and + 3
use these factors to split the x- term
4x² - 4x + 3x - 3 = 0 ( factor the first/second and third/fourth terms )
4x(x - 1) + 3(x - 1) = 0 ← factor out (x - 1) from each term
(x - 1)(4x + 3) = 0 ← in factored form
equate each factor to zero and solve for x
4x + 3 = 0 ( subtract 3 from each side )
4x = - 3 ( divide both sides by 4 )
x = - \(\frac{3}{4}\)
x - 1 = 0 ( add 1 to both sides )
x = 1
solutions are x = - \(\frac{3}{4}\) , x = 1
Answer this question

Answers
Using the Pythagorean theorem and trig identities, it is proved sinθ + cosθ = 1.
The Pythagorean theorem states that for a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
In this case, we can use the Pythagorean theorem to prove that sinθ+cosθ=1.
Let's take a right triangle with an angle θ and sides a, b and c, as shown in the diagram below:
By the Pythagorean theorem, we have:
a² + b² = c²
Now, we can substitute a and b with the trigonometric functions for the sides of our triangle:
sin²θ + cos²θ = 1
We can simplify this expression by using the trigonometric identity:
sin²θ + cos²θ = 1
sin²θ + cos²θ = (sinθ + cosθ)²
Substituting (sinθ + cosθ)² back into the equation, we get:
(sinθ + cosθ)² = 1
Hence, using the Pythagorean theorem and trig identities, it is proved sinθ + cosθ = 1.
To learn more about the trigonometric equation visit:
brainly.com/question/23599274.
#SPJ1
PLEASE HELP ME!!! THANK YOU

Answers
The interval notation for the solution set is (-∞, -4] and the number line is on the image at the end.
How to find the solution set of the ienquality?Here we want to find the solution set of the inequality below:
x ≤ -4
First let's do the interval notation. This will be the set that contains all the numbers from negative infinity to -4 (with -4 included, so we need to have a closed set at that end)
This is written as:
(-∞, -4]
The use of the symbols [ ] means that the element belongs to the set.
Now to the number line, we will have a closed circle at x = -4 (because it is a solution) and a line that goes to the left of it. You can see an example in the graph at the end.
Learn more about inequalities at:
https://brainly.com/question/24372553
#SPJ1

what is the equation of the line that passes through the point (6,-5) and has a slope of -1/6
Answers
The equation of the line that passes through the point (6,-5) and has a slope of -1/6 is y = (-1/6)x - 4.
We know that, the slope intercept form of a line is given by:-
y = mx + c
Where,
m represents the slope of the line,
c represents the y -intercept and,
(x,y) represent the coordinates of each of the ordered pairs in the line
Hence, we can write,
m = -1/6
One of the ordered pairs, (x,y) is (6,-5).
Hence, we can write,
-5 = (-1/6)*6 + c
-5 = -1 + c
c = -5 + 1
c = - 4
Hence, the equation of the line is given by:-
y = (-1/6)x - 4
To learn more about equation of the line, here:-
https://brainly.com/question/21511618
#SPJ1
-2 3/4 divided by 1/2
Answers
Answer:
-11/2
Step-by-step explanation:
Help plssss!!! I would really appreciate it!

Answers
Answer:
The table represents a linear function.
Step-by-step explanation:
Graphed, the points go in a straight line, and you are able to draw a line through it. The equation for the line is y = 4x + 4.
Simplify the following expression. 3 11 5 ÷ 3 − 9 5 A. 12 B. 1 81 C. 81 D.
Answers
Answer:
A
Step-by-step explanation:
To simplify the expression 3 11 5 ÷ 3 − 9 5, let's break it down step by step:
First, let's simplify the division 3 11 5 ÷ 3:
3 11 5 ÷ 3 = (3 × 115) ÷ 3 = 345 ÷ 3 = 115.
Next, let's subtract 9 5 from the result we obtained:
115 - 9 5 = 115 - (9 × 5) = 115 - 45 = 70.
Therefore, the simplified expression is 70.
The correct answer is A. 70.
Using the given information, find the mean, median, and mode.

Answers
To calculate the mean, median, and mode, we first need to know what each of these terms represents. The mean, also known as the average, is the sum of all the values divided by the total number of values. To find the mean, add up all of the values and divide by the number of values. The median is the middle value in a set of data when it is arranged in order from least to greatest. The mode is the value that occurs most frequently in a set of data. Here's an example to illustrate these concepts:
Let's say we have a set of data consisting of the following values: 2, 5, 5, 7, 8, 10, 12. To find the mean, we add up all of the values and divide by the number of values. In this case, the sum of the values is 49 (2+5+5+7+8+10+12) and there are 7 values, so we divide 49 by 7 to get the mean, which is approximately 7. To find the median, we first need to arrange the data in order from least to greatest: 2, 5, 5, 7, 8, 10, 12. The middle value is 7, so that is the median. To find the mode, we look for the value that occurs most frequently. In this case, 5 occurs twice, which is more than any other value, so the mode is 5.
In conclusion, the mean, median, and mode are all measures of central tendency that can be used to describe a set of data. The mean is the average value, the median is the middle value, and the mode is the value that occurs most frequently. When calculating these measures, it is important to carefully consider the data and choose the appropriate method for finding each value.
For such more question on median
https://brainly.com/question/26177250
#SPJ8
Hot chocolate mix cost $6.48 for 3 boxes. How much does one box cost?
Answers
Answer:
$2.16
Step-by-step explanation:
The rate is \(\frac{6.48}{3} \\\).
Divide it to get one box:
6.48 ÷ 3 = 2.16
Therefore, one box of hot chocolate mix costs $2.16.
what is the kinetic energy of 1500 kg pick-up truck traveling at 31.0 m/sec.
Answers
The kinetic energy of a 1500 kg pick-up truck traveling at 31.0 m/sec will be 720 kJ.
What is kinetic energy?If the body of the mass (m) is moving with a velocity (v), then the body possesses the energy which is known as kinetic energy. The SI unit of the kinetic energy is Joule. Then the formula is given as,
KE = 1/2 x mv²
The kinetic energy of a 1500 kg pick-up truck traveling at 31.0 m/sec is given as,
KE = 1/2 x 1500 x 31²
KE = 720,750 Joule
KE = 720 kJ
The kinetic energy of a 1500 kg pick-up truck traveling at 31.0 m/sec will be 720 kJ.
More about the kinetic energy link is given below.
https://brainly.com/question/26472013
#SPJ9
What is the answer to this question and how to solve?

Answers
Answer:
Line ZL and line LZ.
Step-by-step explanation:
Since it is a line (because a line needs to have two or more points to be able to graph), it can be represented in two ways. The first being ZL, and the second being LZ.
Brainliest please.
Answer:
Step-by-step explanation
Oh
Suppose that the distribution of monthly revenues of a new startup business is not symmetric.
According to Chebyshev's Theorem, at least approximately what percentage of the revenues are within k=3.3 standard deviations of the mean?
Answers
According to Chebyshev's Theorem, approximately 91% of the revenues are within k = 3.3 standard deviations of the mean.
What is Chebyshev's Theorem?
The minimum percentage of observations that are within a given range of standard deviations from the mean is calculated using Chebyshev's Theorem. Several other probability distributions can be applied to this theorem. Chebyshev's Inequality is another name for Chebyshev's Theorem. For a large class of probability distributions, Chebyshev's inequality ensures that no more than a specific percentage of values can deviate significantly from the mean.
According to Chebyshev's Theorem, at least 1 - 1/k² of the revenues lie within k standard deviations of the mean.
So when k = 3.3
1 - 1/k² = 1 - 1/3.3² = 1 - 0.0918 = 0.9082 = 90.82% ≈ 91%
Therefore according to Chebyshev's Theorem, approximately 91% of the revenues are within k = 3.3 standard deviations of the mean.
To learn more about Chebyshev's Theorem, follow the link.
https://brainly.com/question/5179184
#SPJ1
if you’re good with set theory for math 30 please help with questions 34, 35, and 36!! real answers only !

Answers
Answer: 34) 15 35) 4, 4, 3 36) 1, 4
Step-by-step explanation:
34)
Let Triangle = T, Circle = C, and Square = S, and Pentagon = P
Top Row: 4T = 8 --> T = 2
2nd column: 2T + 2C = 10 --> C = 3
2nd row: S + T + 2C = 12 --> S = 4
1st column: T + 2S + P = 15 --> P = 5
3rd column: x = T + C + 2P
= 2 + 3 + 2(5)
= 15
35)
Fill in the puzzle as follows:
\(\begin{array}{cccc}2&4&1&\bold{3}\\3&1&\bold{4}&2\\1&2&3&4\\\bold{4}&3&2&1\end{array}\)
A = 4, B = 4, C = 3
36)
Notes:
U = {x | 3 ≤ x < 14, x ∈ N}
means that everything within the rectangular box (including the circles) contains the Natural Numbers of 3 through 14, including 3 but excluding 14.
R = {x | 5 ≤ x ≤ 8, x ∈ N}
means that everything within the circle of R (including the intersection with T) contains the Natural Numbers of 5 through 8, including 5 and 8.
T = {4, 7, 10, 13}
means that everything within the circle of T (including the intersection with R) contains 4, 7, 10, & 13.
Filling in the Venn Diagram (from left to right):
R (only) contains 5, 6, 8
R ∩ T (the middle section of R and T) contains 7
T (only) contains 4, 10, 13
outside the circles but inside the rectangle (usually written on the lower left corner) is 3, 9, 11, 12
Statements:
1) R ∩ T = {7}
means the intersection of R and T (the middle circle) contains 7 and nothing else.
Refer to your Venn Diagram. This statement is TRUE!
2) n(R ∪ T)' = 6
means the QUANTITY of numbers NOT in both R & T is 6.
The numbers that are not in either R or T are: 3, 9, 11, 12.
That results in 4 numbers (not 6). This statement is False.
3) n(R' ∩ T) = 2
means the QUANTITY of numbers that are NOT in R but are in T is 2.
The numbers that are not in R but are in T are: 4, 10, 13.
That results in 3 numbers (not 2). This statement is False.
4) n(R ∩ T') = 3
means the QUANTITY of numbers that are in R but NOT in T is 3.
The numbers that are in R but NOT in T are: 5, 6, 8.
That results in 3 numbers. This statement is True!
A baseball team has scheduled its opening game for April 1. If it rains on April 1, the game is postponed and will be played on the next day that it does not rain. The team purchases insurance against rain. The policy will pay 1000 for each day, up to 2 days, that the opening game is postponed. The insurance company determines that the number of consecutive days of rain beginning on April 1 is a Poisson random variable with mean 0.6.
Required:
What is the standard deviation of the amount the insurance company will have to pay?
Answers
Please help me with this problem

Answers
Answer:
B
Step-by-step explanation:
Please try and answer my questions aswell :) have good day
In the figure, m∠4=74°
and m∠3=43°
. Find m∠1
and m∠2
.

Answers
Answer:
Based on the information given, we know that angles 3 and 4 are supplementary (they add up to 180 degrees) and angles 2 and 4 are vertical angles (they are congruent). Therefore, we can write:
m∠4 + m∠3 = 180 (since angles 3 and 4 are supplementary)
m∠4 = m∠2 (since angles 2 and 4 are vertical angles)
Substituting m∠4 = m∠2 into the first equation, we get:
m∠2 + m∠3 = 180
Now we can solve for m∠2 and m∠3:
m∠3 = 43 (given)
m∠2 = 180 - m∠3 = 180 - 43 = 137
Since angles 1 and 2 are also supplementary, we can find m∠1 by subtracting m∠2 from 180:
m∠1 = 180 - m∠2 = 180 - 137 = 43
Therefore, m∠1 = 43 degrees and m∠2 = 137 degrees.
Pre calc, question 10, make the answer bold please, Thanks!

Answers
given:
f(x) = -1/4(x) - 1
To find the inverse; first we solve for x and then we change the variables, as follows:
y = -1/4(x) - 1
y - 1 = -1/4(x)
x = -4y - 4; so:
f⁻¹(x) = -4x - 4
Graphs: (red one is the original and blue comes into the inverse)

what is 8 2/10 minus 4 1/3
Answers
Answer:
Convert the mixed numbers to improper fractions, then find the LCD and combine.
Exact Form:
58 /15
Decimal Form:
3.8 6
Mixed Number Form:
3 13 /15
Step-by-step explanation:
=8+21−4−13
=
8
+
2
1
−
4
−
1
3
Solving the whole number parts
8−4=4
8
−
4
=
4
Solving the fraction parts
21−13=?
2
1
−
1
3
=
?
Find the LCD of 2/1 and 1/3 and rewrite to solve with the equivalent fractions.
LCD = 3
63−13=53
6
3
−
1
3
=
5
3
Simplifying the fraction part, 5/3,
53=123
5
3
=
1
2
3
Combining the whole and fraction parts
4+1+23=523
The answer is 5 2/3
g A zoologist spots what might be a rare subspecies of beetle, due to the pattern on its back. In the rare subspecies, 98% have the pattern. In the common subspecies, 5% have the pattern. The rare subspecies accounts for 1% of the population. Given that a beetle has the pattern, what is the probability that it belongs to the rare subspecies
Answers
Answer:
Given that a beetle has the pattern, 0.098 is the probability that it belongs to the rare subspecies
Step-by-step explanation:
Probability of having a pattern in rare subspecies \(= 0.98\\\)
Percentage of rare subspecies = 1 % = 0.01
Probability of a beetle with pattern belonging to rare subspecies is
\(=0.01 * 0.98 \\= 0.098\)
thirty is equal to twice a number decreased by four
Answers
Answer:
4-(2n)= 30
Step-by-step explanation:
N is 17
determine what type of model bets fits the given situation: A $500 raise in salary each year
Answers
The type of model that best fits the situation of a $500 raise in salary each year is a linear model.
In a linear model, the dependent variable changes a constant amount for constant increments of the independent variable.
In the given case, the dependent variable is the salary and the independent variable is the year.
You may build a table to show that for increments of 1 year the increments of the salary is $500:
Year Salary Change in year Change in salary
2010 A - -
2011 A + 500 2011 - 2010 = 1 A + 500 - 500 = 500
2012 A + 1,000 2012 - 2011 = 1 A + 1,000 - (A + 500) = 500
So, you can see that every year the salary increases the same amount ($500).
In general, a linear model is represented by the general equation y = mx + b, where x is the change of y per unit change of x, and b is the initial value (y-intercept).
In this case, m = $500 and b is the starting salary: y = 500x + b.
Which set of three angles could represent the interior angles of a triangle?

Answers
Answer:
As a claustrophobia, I can ????
O 35°, 35°, 20°
Please help and show work
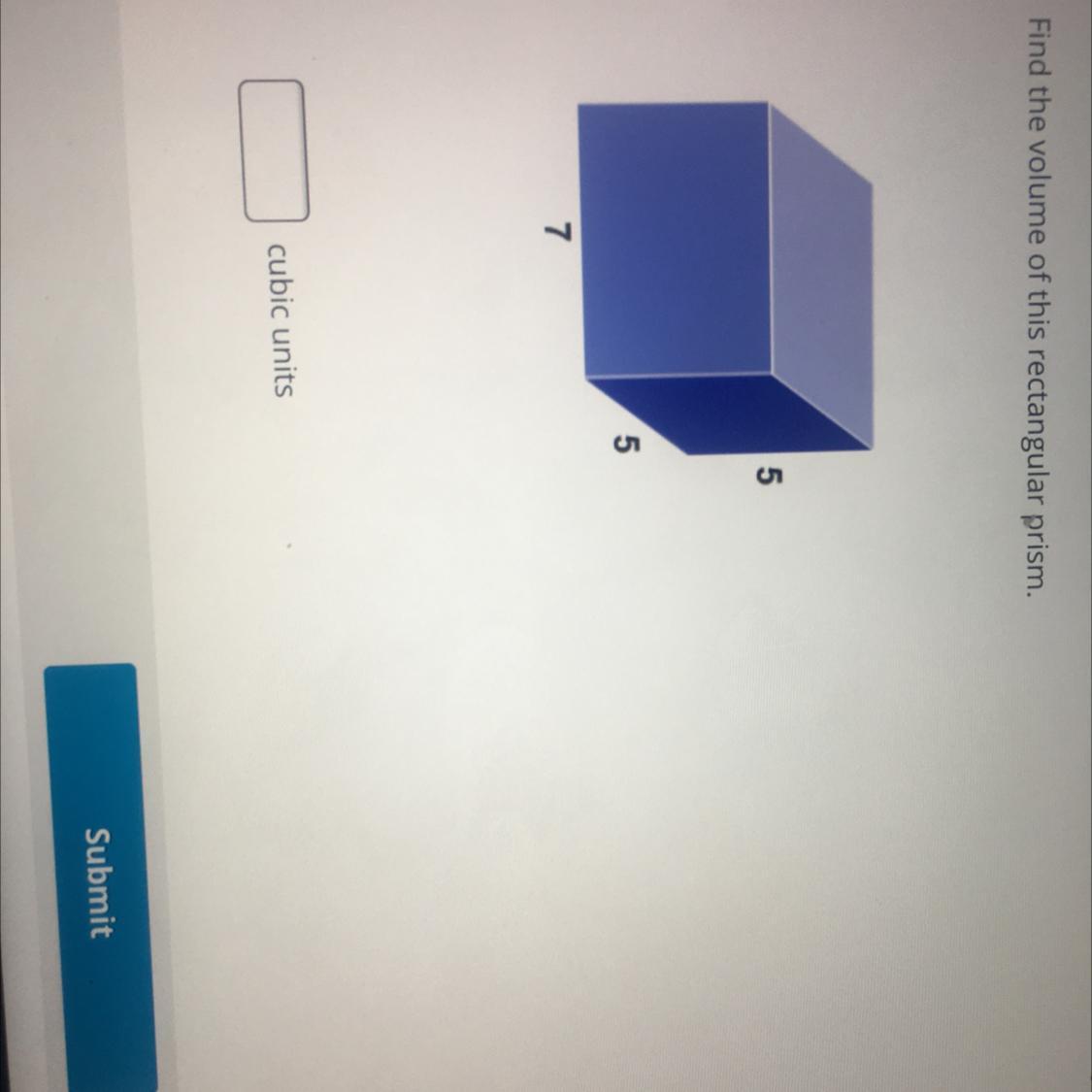
Answers
Answer:
175 is the answer
Step-by-step explanation:
5x5=25
25x7=175