I have a bag containing red, green, blue, and white marbles and the ratio $\text{red}:\text{green}:\text{blue}:\text{white}$ is $2:2:5:7$. I have 304 marbles. How many blue marbles do I have?
Answers
Answer:
95
Step-by-step explanation:
Let 2x be how many red/green marbles there are,
let 5x be how many blue marbles there are, and
let 7x be how many white marbles there are.
2x + 2x + 5x + 7x = 304
16x = 304
x = 19
As 5x is defined as how many blue marbles there are, we could just plug x for 19:
5*19 = 95
I hope this helped, and if it did please consider giving me brainliest :)
Answer:
95
Step-by-step explanation:
Let r, g, b, w be the number of red, green, blue, and white marbles, respectively. Since r : g : b : w = 2 : 2 : 5 : 7, there is some value of x for which r = 2 x, g = 2x, b = 5x, and w = 7x. Then, we have
304 = r + g + b + w
= (2x) + (2x) + (5x) + (7x)
= 16x
Dividing both sides of 16x = 304 by 16 gives x=19. This gives us r = 38, g = 38, b = 95, w = 133, so I have 95 blue marbles.
Related Questions
Please help me with this question

Answers
The depth of the water if the speed of the tsunami is 10 m/s is approximately 0.34 meters, or 34 centimeters, given by the equation d = s / (3v).
What is speed?Speed is the rate at which an object moves through a distance per unit of time. It is often expressed in meters per second (m/s) or kilometers per hour (km/h).
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It usually contains variables, constants, and mathematical operations, and can be solved to find the value of the variables.
According to the given information:
The equation relating the speed of a tsunami and the depth of the water is s = 3vd, where s is the speed of the wave (in m/s), v is the velocity of gravity (which is approximately 9.8 m/s²), and d is the depth of the water (in meters).
We can rearrange the equation to solve for d, which gives us:
d = s / (3v)
Plugging in the given values, we get:
d = 10 m/s / (3 × 9.8 m/s²)
Simplifying, we get:
d = 10 / 29.4
Therefore, the depth of the water is approximately 0.34 meters, or 34 centimeters.
So, if the speed of the tsunami is 10 m/s, the depth of the water is approximately 0.34 meters.
To know more about equation, speed visit:
https://brainly.com/question/751218
#SPJ1
Find the fraction and the ratio of No. Of prime numbers to the numbers up to 50
Answers
Answer:
3/ 10
Step-by-step explanation:
Count of numbers up to 50 = 50
Prime numbers up to 50 :
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}
Count of prime numbers up to 50 = 15
Hence, ratio of prime numbers to all numbers ;
15 : 50
3 / 10
Solve 2 log x = log 64. (1 point)
Answers
Answer:
8
Step-by-step explanation:
2log(x)=log(64)
By logarithms properties
\(xlog_{a}(b)=log_{a}(b^{x} ) \\\)
log(x²)=log(64)
When you have log or ln in both sites, you delete them and...
x²=64
\(\sqrt[]{x^{2} } =\sqrt{64} \\x=8\)
Write only vertical translation
And horizontal translation
For best answer I give brainiest!

Answers
Answer:
I hope this helps
Ex: vertical translation |x+5|-2 the graph will shift down 2 units. Or the same as (x+5)+2 in this case the graph will shift up 2 units.
Horizontal translation |x+5|-2 the graph will shift to the left 5 units. Or same as (x-5)-2 in this case the graph will shift over to the right 5 units.
Step-by-step explanation:
Vertical translation is when a graph is being shifted up or down.
Horizontal translation is when a graph is being shifted over left or right.
find the area of the triangle formed by the vertex and x-intercepts of parabola y=-x^2-3x+10
Answers
Answer:
42.875
Step-by-step explanation:
First you find the x-intercepts and the vertex of the equation.
(-5, 0), (-2, 0), (-3/2, 49/4)
You use those coordinates to find the sides of the triangle and then you use the lengths to find the semiperimeter.
Lastly, you use Heron's formula to compute the area.
The area of the triangle is required.
The area of the triangle is \(42.875\ \text{units}^2\)
\(y=-x^2-3x+10\)
The x intercepts are
\(-x^2-3x+10=0\\\Rightarrow x=\dfrac{-\left(-3\right)\pm \sqrt{\left(-3\right)^2-4\left(-1\right)\times 10}}{2\left(-1\right)}\\\Rightarrow x=-5,2\)
The x intercepts are
\((-5,0),(2,0)\)
Distance between them is
\(2-(-5)=7\ \text{units}\)
Vertex of a parabola is given by
\(x=-\dfrac{b}{2a}\\ =-\dfrac{-3}{2\times -1}\\ =-1.5\)
\(y=-(-1.5)^2-3(-1.5)+10=12.25\)
So,
Base = b = 7 units
Height = h = 12.25 units
Area is
\(A=\dfrac{1}{2}bh\\\Rightarrow A=\dfrac{1}{2}\times 7\times 12.25\\\Rightarrow A=42.875\ \text{units}^2\)
Learn more:
https://brainly.com/question/11952845?referrer=searchResults
An object shot into the air follows the path given by
r (t) = < at, bt − 4.9t2 >m
with t in seconds and a and b are unknown physical constants.
The launch speed is 500 m/s. If you need the object to land 14,000 meters downrange, what launch angle should you use? Measure the angle in degrees, counter-clockwise from the positive horizontal direction. Be accurate to two decimal places.
degrees
Answers
To land 14,000 meters downrange, the launch angle of the object should be approximately 38.88 degrees.
The horizontal distance traveled by the object is given by:
Range = R = b * t
where b is the coefficient of t in the r(t) equation.
The time taken by the object to reach the maximum height can be found by setting the vertical component of the velocity to zero:
v_y = b - 9.8t = 0
t = b/9.8
The maximum height attained by the object can be found by substituting the value of t in the r(t) equation:
h_max = r(b/9.8) = ab^2/(2 * 9.8)
The range can also be expressed in terms of the launch speed v and the launch angle θ:
R = v^2 * sin(2θ) / g
where g is the acceleration due to gravity.
Equating the two expressions for R, we get:
b * (2 * v^2 / g) * sin(θ) * cos(θ) = v^2 * sin(2θ) / g
tan(θ) = (2 * 4.9 * b) / (500)^2
θ = arctan[(2 * 4.9 * b) / (500)^2]
Substituting the value of b in terms of a, we get:
θ = arctan[(2 * 4.9 * a * tan(θ)) / (500)^2]
Using numerical methods or a graphical approach, we can find that the launch angle that gives a range of 14,000 meters is approximately 38.88 degrees.
For more questions like Downrange click the link below:
https://brainly.com/question/14570098
#SPJ11
HELP PLEASEEEEEEEEEEEEEEEEWEE

Answers
Steps:
b = measure 2
4b + b = 100
5b = 100
b = 100/5
b = 20
Check:
4(20) + 20 = 100
80 + 20 = 100
100 = 100 ✅
What is the area of the hexagon? 5 cm 8 cm 9.28 cm

Answers
Answer:
57.12 cm²
Step-by-step explanation:
The given dimensions of the hexagon are;
The side length of the hexagon, s = 5 cm
The distance across flats = 8 cm
The distance across corners = 9.28 cm
The area of a regular hexagon, 'A', is given as follows;
\(A = \dfrac{3 \cdot \sqrt{3} }{2} \cdot s^2= \dfrac{1}{2} \cdot P \cdot a = 3\cdot s\cdot h\)
Where;
a = The side length of the hexagon
P = The perimeter of the hexagon
h = The height of one of the triangles in the hexagon
However with the given dimensions, the area of the hexagon can be found by finding the sum of the areas of the triangles that make up the rectangle
A₁ = A₃ = A₄ = A₆ = (1/2) × 4.64 cm × 4 cm = 9.28 cm²
A₂ = A₅ = (1/2) × 5 cm × 4 cm = 10 cm₂
The area of the hexagon, A = A₁ + A₃+ A₄ + A₆ + A₂ + A₅ = 4 × A₁ + 2 × A₂
∴ A = 4 × 9.28 cm² + 2 × 10 cm² = 57.12 cm²
2 × (5×4/2 + 2×9.28/4×4) = 57.12 cm²
The area of the hexagon, A = 57.12 cm²

Based on the above data, if an individual exercises 20 minutes daily, his predicted % body fat would be _________.
Answers
If an individual exercises 20 minutes daily, the predicted percentage of body fat would be approximately 21.63%.
To determine the predicted percentage of body fat for an individual who exercises 20 minutes daily, we can use linear regression to estimate the relationship between exercise duration and percentage of body fat.
First, let's calculate the slope and intercept of the regression line:
Mean of Exercise (min):
(10 + 18 + 26 + 33 + 44) / 5 = 22.2
Mean of % Fat:
(30 + 25 + 18 + 17 + 14) / 5 = 20.8
Calculate the deviations from the means for Exercise (min) and % Fat:
Exercise (min) deviations: 10 - 22.2, 18 - 22.2, 26 - 22.2, 33 - 22.2, 44 - 22.2
% Fat deviations: 30 - 20.8, 25 - 20.8, 18 - 20.8, 17 - 20.8, 14 - 20.8
Sum of the product of the deviations:
Σ(Exercise deviation × % Fat deviation) = (10 - 22.2) × (30 - 20.8) + (18 - 22.2) × (25 - 20.8) + (26 - 22.2) × (18 - 20.8) + (33 - 22.2) × (17 - 20.8) + (44 - 22.2) × (14 - 20.8)
Sum of Exercise (min) deviations squared:
Σ(Exercise deviation²) = (10 - 22.2)² + (18 - 22.2)² + (26 - 22.2)² + (33 - 22.2)² + (44 - 22.2)²
Calculate the slope (b):
b = Σ(Exercise deviation × % Fat deviation) / Σ(Exercise deviation²)
Calculate the intercept (a):
a = mean of % Fat - (slope × mean of Exercise)
Now we can substitute the given exercise duration of 20 minutes into the equation to find the predicted percentage of body fat:
Predicted % Fat = a + (b × 20)
Let's calculate these values:
Exercise deviations: -12.2, -4.2, 3.8, 10.8, 21.8
% Fat deviations: 9.2, 4.2, -2.8, -3.8, -6.8
Σ(Exercise deviation × % Fat deviation) = (-12.2 × 9.2) + (-4.2 × 4.2) + (3.8 × -2.8) + (10.8 × -3.8) + (21.8 × -6.8) = -305.24
Σ(Exercise deviation²) = (-12.2)² + (-4.2)² + (3.8)² + (10.8)² + (21.8)² = 1154.68
b = (-305.24) / 1154.68 ≈ -0.2648
Mean of Exercise (min) = 22.2
Mean of % Fat = 20.8
a = 20.8 - (-0.2648 × 22.2) ≈ 26.9496
Predicted % Fat = 26.9496 + (-0.2648 ² 20) ≈ 21.63
Therefore, if an individual exercises 20 minutes daily, the predicted percentage of body fat would be approximately 21.63%.
Learn more about linear regression click;
https://brainly.com/question/32505018
#SPJ4
Complete question =
A researcher collects data on the relationship between the amount of daily exercise an individual gets and the percent body fat of the individual. The following scores are recorded.
Individual: 1, 2, 3, 4, 5
Excercise (min): 10, 18, 26, 33, 44
% Fat: 30, 25, 18, 17, 14
Based on the above data, if an individual exercises 20 minutes daily, his predicted % body fat would be ?
21.63
27.74
27.88
23.75
gross margin is calculated by subtracting ______ from ______.
Answers
Gross margin is calculated by subtracting the cost of goods sold from the total revenue.
To understand this calculation more comprehensively, let's break it down:
1. Total Revenue: Total revenue represents the total amount of money generated from the sales of goods or services.
It includes the selling price of the products or services and any additional income related to sales, such as shipping charges or discounts.
2. Cost of Goods Sold (COGS): Cost of Goods Sold refers to the direct costs incurred in producing or acquiring the goods that were sold.
It includes expenses such as the cost of raw materials, manufacturing costs, labor costs directly associated with production, and any other expenses directly tied to the production of goods.
By subtracting the COGS from the total revenue, we arrive at the gross margin, which represents the amount of money remaining after accounting for the direct costs associated with the production or acquisition of the goods sold.
Gross margin reflects the profitability of the core business operations before considering other indirect expenses such as overhead costs, marketing expenses, or administrative costs.
The formula for calculating gross margin can be represented as follows:
Gross Margin = Total Revenue - Cost of Goods Sold
To know more about Gross margin refer here:
https://brainly.com/question/30890680#
#SPJ11
4.5kg of bananas and 3.5kg of apples cost £6.75. ^kg of apples cost £5.40. Calculate the cost of 1kg of bananas.
Answers
Answer: Let's assume the cost of 1 kilogram of bananas is represented by 'x'.
According to the given information, 4.5 kg of bananas and 3.5 kg of apples together cost £6.75. We also know that the cost of 1 kg of apples is £5.40.
Using this information, we can set up the following equation:
4.5x + 3.5(£5.40) = £6.75
Now let's solve for 'x':
4.5x + 3.5(£5.40) = £6.75
4.5x + £18.90 = £6.75
4.5x = £6.75 - £18.90
4.5x = -£12.15
x = (-£12.15) / 4.5
x ≈ -£2.70
The cost of 1 kilogram of bananas, based on this calculation, is approximately -£2.70. However, it's important to note that a negative cost doesn't make sense in this context. It's possible there may be an error in the given information or the setup of the equation.
Find the equation of the line with a slope of 1/5 that passes through the point (10,9).
Answers
Answer:
The equation of the line with a slope of 1/5 that passes through the point (10,9) is:
\(y=\frac{1}{5}x+7\)Step-by-step explanation:
Given
Slope = m = 1/5
Point (10, 9)
To Determine
An equation of the line with a slope of 1/5 that passes through the point (10,9).
We know that the point-slope form of the line equation is
\(y-y_1=m\left(x-x_1\right)\)
where
m is the slope of the line(x₁, y₁) is the pointsubstituting the values m = 1/5 and the point (10, 9) in the equation
\(y-y_1=m\left(x-x_1\right)\)
\(y-9=\frac{1}{5}\left(x-10\right)\)
Add 9 to both sides
\(y-9+9=\frac{1}{5}\left(x-10\right)+9\)
\(y=\frac{1}{5}x-2+9\)
\(y=\frac{1}{5}x+7\)
Therefore, the equation of the line with a slope of 1/5 that passes through the point (10,9) is:
\(y=\frac{1}{5}x+7\)Explain how to depict the five numbers visually with a boxplot. Choose the correct answer below. Select all that apply.
O A. Draw a number line that spans all the values in the data set. Enclose the values from the lower to upper quartile in a box. Draw a vertical line through the box at the mean
O B. Draw a number line that spans all the values in the data set. Enclose the values from the lower to upper quartile in a box.
O C. Draw a number line that spans all the values in the data set. Enclose the values from the lower to upper quartile in a box. Draw a vertical line through the box at the median. Add "whiskers" extending to the low and high values.
O D. Draw a number line that spans all the values in the data set. Enclose the values from the lower to upper quartile in a box. Draw a vertical line through the box at the mean. Add "whiskers" extending to the low and high values.
Answers
C. Draw a number line that spans all the values in the data set. Enclose the values from the lower to upper quartile in a box. Draw a vertical line through the box at the median. Add "whiskers" extending to the low and high values.
Draw a number line that spans all the values in the data set. Enclose the values from the lower to upper quartile in a box. Draw a vertical line through the box at the median. Add "whiskers" extending to the low and high values. Quartiles are three values that divide the statistical data into four parts, each containing the same observation. A quarter is a type of quantity. First quartile: Also called Q1 or lower quartile. Second quartile: Also called Q2 or median. Third quarter: Also called Q3 or upper quarter.
Quartiles are values that divide a list of numeric data into quarters. The three-quarter median measures the center of the distribution and shows the data near the center. The lower half of the quartile represents only half of the dataset below the median, and the upper half represents the remaining half above the median. In summary, quartiles describe the distribution or distribution of a data set.
Learn more about Quartile:
brainly.com/question/24329548
#SPJ11
What is the greatest common factor of 16 , 24 , 48
Answers
Answer:
8
Step-by-step explanation:
The biggest common factor number is the GCF number. So the Greatest Common Factor 16, 24, 48 is 8.
please make my answer as brainelist
brainliest. please help
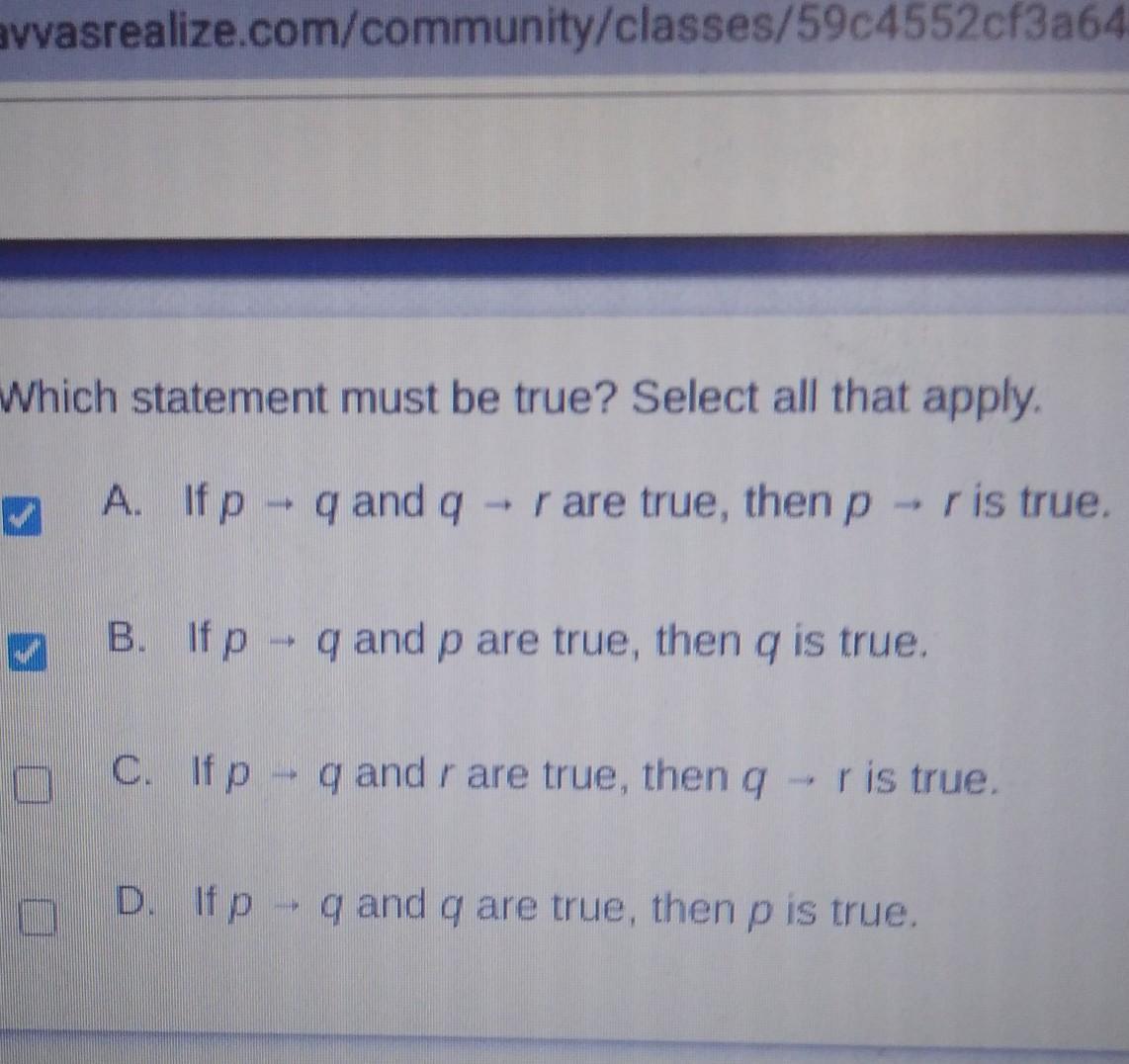
Answers
PLEASE HALP FAST ILL GIVE BRAINLIESTTT

Answers
Answer:
no one is equivalent to it
Harry goes to Hogwarts School of Witchcraft and Wizardry. He can travel to school and back in
3
33 different ways: by the Hogwarts Express, a flying car, or the Knight Bus. He's decided to choose his methods of transportation to and from Hogwarts at random this year.
Which of these tables lists all the different ways Harry can get to Hogwarts and back? (Each row represents one outcome.)
Choose all answers that apply:
Choose all answers that apply:
(Choice A) Table A
A
Table A
(Choice B) Table B
B
Table B
Table A:
To Hogwarts From Hogwarts
Knight Bus Knight Bus
Knight Bus Flying Car
Knight Bus Hogwarts Express
Flying Car Knight Bus
Flying Car Flying Car
Flying Car Hogwarts Express
Hogwarts Express Knight Bus
Hogwarts Express Flying Car
Hogwarts Express Hogwarts Express
Table B:
To Hogwarts From Hogwarts
Knight Bus Hogwarts Express
Flying Car Flying Car
Hogwarts Express Knight Bus
Knight Bus Knight Bus
Flying Car Hogwarts Express
Hogwarts Express Flying Car
Knight Bus Flying Car
Flying Car Knight Bus
Hogwarts Express Hogwarts Express
Answers
Table B lists all the different ways Harry can get to Hogwarts and back. See the attached tables.
What explanation justifies the above?One mus tnote that both tables detail all of the alternative routes Harry can take to and from Hogwarts, however Table B is the only one that lists all of the different modes of transportation.
Table B includes all of the potential scenarios in which Harry can use the Knight Bus, Flying Car, or Hogwarts Express to and from Hogwarts, including situations in which he uses the same form of transportation both times. Table A, on the other hand, simply covers transit combinations, not all conceivable outcomes. So it is correct to state that as a result, Table B is the right solution.
See attached tables.
Learn more about Tables:
https://brainly.com/question/10670417
#SPJ1

rewrite the equation so that y is a function of x. 2x+y = 7
Answers
What is the conversion of 2/5 in decimal ?
Answers
The conversion of a fraction number with denominator 5 and numerator 2 , 2/5 in decimals is equals to the 0.4 value.
A decimal number can be defined as a number whose whole number part and fractional part are separated by a decimal point. Writing 2/5 as a decimal number by converting the denominator to powers of 10. We multiply the numerator and denominator by a number so that the denominator is a power of 10.
2/5 = (2 × 2) / (5 × 2) = 4/10
Now move the decimal point to the left as many places as there are zeros in the denominator, which is a power of 10.
The decimal moved one place to the left because the denominator was 10. Therefore, 4/10 = 0.4. Hence, required value is 0.4.
To learn more about decimal, visit:
https://brainly.com/question/703656
#SPJ4
Sahara started the day with $80
.
She spent $60
.
What fraction of her money has Sahara spent?
Give your answer as a fully simplified fraction.
Answers
Answer:
She spent 3/4 of her money
Step-by-step explanation:
60/80 is .75, which translates to 3/4.
Answer:
3/4 or 75%
Step-by-step explanation:
60$/80$ = 3/4
What is the slope of a line that is perpendicular to the line y= -2/3x + 4?
Answers
Answer:
\( \frac{3}{2} \)
Step-by-step explanation:
Since the given line is in the slope- intercept form, its gradient can be seen from the coefficient of x, which is -2/3.
The product of the slopes of perpendicular lines is -1.
Let the slope of the line be m.
\(m( - \frac{2}{3} ) = - 1\)
\( m = - 1 \div ( - \frac{2}{3} )\)
\(m = - 1 \times ( - \frac{3}{2} )\)
\(m = \frac{3}{2} \)
Thus the slope of the line is 3/2.
How do you solve this anyone??? Triangle lmn is a dialation of triangle lmn. Find the scale factor of the dilation an classify it as an enlargement or a reduction.
Answers
Answer:
Triangle L'M'N' is an enlargement of triangle LMN
Suppose your parents agree to pay you
one cent today, two cents tomorrow (the first day after today), four cents the next day (second day after today), and so forth. Each time they double the amount they pay you. Write an equation expressing amount paid in terms of number of days after today. What kind of function is this? How much will they pay you the 30th day? Surprising?! Show that the amount paid today (0 days after today) agrees with the definition of zero exponents.
Answers
They will pay You $5368709.12 on the 30th day
What does the term "compound interest" mean?
Compound interest is when you receive interest on both your interest income and your savings.
You start with a one cent.
You have $0.01 x 2 the following day.
You have $0.01 x 2 x 2 the following day.
and so forth
You will have $0.01 x 2^n-1 on day n.
This means that on the 30th day, you have $0.01 x 2^29 = $5 368 709.12.
That is compound interest at work! It equates to daily payments of 100% interest. It immediately soars to inconceivable heights with even a penny as your initial investment!
Learn more about compound interest
https://brainly.com/question/24274034
#SPJ1
one spinner has three same-sized sectors labeled r, s, and t. a second spinner has two same-sized sectors labeled 3 and 5. each spinner is spun once. what is the sample space of outcomes?
Answers
The sample space of outcomes of the given experiment is {r3, r5, s3, s5, t3, t5}
One spinner has three same-sized sectors labeled = r, s and t
A second spinner has two same-sized sectors labeled = 3 and 5
Given that the each spinner is spun once
The sample space is defined as the set of all possible outcomes of the random experiments. Usually the sample space of the random experiment is represented by the letter S.
Here,
The sample spaces are
= {r3, r5, s3, s5, t3, t5}
The total number of outcomes = 6
Therefore, the sample space is {r3, r5, s3, s5, t3, t5}
Learn more about sample space here
brainly.com/question/28043513
#SPJ4
Find an equation equivalent to 2x + 3y = 6 in polar coordinates.
Answers
PLEASE GIVE ME BRAINLIEST! :)
Answer:
2 cos(θ) + 3 sin(θ) = 6/r
Step-by-step explanation:
To convert the equation 2x + 3y = 6 to polar coordinates, we need to express x and y in terms of r and θ.
Using the fact that x = r cos(θ) and y = r sin(θ), we get:
2(r cos(θ)) + 3(r sin(θ)) = 6
Simplifying this equation, we get:2r cos(θ) + 3r sin(θ) = 6
Dividing both sides by r, we get:2 cos(θ) + 3 sin(θ) = 6/r
This is an equation equivalent to 2x + 3y = 6 in polar coordinates.
500 gallon tank contain 200 gallons of water with 100ib of salt water containing 1ib of salt per gallon is entering at a rate of 3 gal/min and the mixture flows out at 2 gal./min. Find the amount of salt in the tank at any time prior to the instant when the solution begins to overflow. Find the concentration (in pounds per gallon) of salt in the tank when it is on the point of overflowing.
Answers
Summary:
To find the amount of salt in the tank at any time prior to overflowing and the concentration of salt when the tank is on the point of overflowing,
Let t be the time in minutes and S(t) be the amount of salt in the tank at time t. The rate of change of salt in the tank is given by the difference between the rate at which saltwater enters and the rate at which the mixture flows out. The rate at which saltwater enters the tank is 3 gallons per minute with a salt concentration of 1 pound per gallon, so the rate of salt entering is 3 pounds per minute. The rate at which the mixture flows out is 2 gallons per minute, which is equivalent to the rate at which the saltwater mixture flows out.
Using the principle of conservation of mass, we can set up the following differential equation: dS/dt = (3 lb/min) - (2 gal/min) * (S(t)/500 gal), where S(t)/500 represents the concentration of salt in the tank at time t. This differential equation can be solved to find the function S(t).
To find the concentration of salt in the tank when it is on the point of overflowing, we need to determine the time t at which the tank is full. This occurs when the volume of water in the tank reaches its capacity of 500 gallons. At that point, we can calculate the concentration of salt, S(t)/500, to find the concentration in pounds per gallon.
Learn more about principle of conservation of mass here:
https://brainly.com/question/9530080
#SPJ11
How do you write 1.27 repeating as a fraction
btw the repeating part is 7
Answers
Answer:
1 27/100
Step-by-step explanation:
Need a little help with this question.

Answers
Answer:
sorry we can't
Step-by-step explanation:
A ailen maked that thats cazy
Answer: 15
Step-by-step explanation:
when 2 sides have the same angle, it means it's isosceles..

Evaluate the expression 2p - (p + 3) +3. For p = 6
Use the CER strategy to show your work.
Answers
Answer: 9
Step-by-step explanation: sorry if it is wrong
Answer:
0
Step-by-step explanation:
2p - (p + 3) + 3
2(6) - (6 + 3) + 3
12 - (9) + 3
12 - 12 = 0
Assume that X, the starting salary offer for education majors, is normally distributed with a mean of $46,292 and a standard deviation of $4,320. The probability that a randomly selected education major received a starting salary offer greater than $52,350 is_____. The probability that a randomly selected education major received a starting salary offer between $45,000 and $52,350 is________. (Hint: The standard normal distribution is perfectly symmetrical about the mean, the area under the curve to the left (and right) of the mean is 0.5. Therefore, the area under the curve between the mean and a z-score is computed by subtracting the area to the left (or right) of the z-score from 0.5.) What percentage of education majors received a starting offer between $38,500 and $45,000? a. 65.38% b. 6.68% c. 93.32% d. 34.62% Twenty percent of education majors were offered a starting salary less than______.
Answers
The given problem statement can be solved by using the z-score formula, that is z = (x - μ)/ σ where x is the value, μ is the mean and σ is the standard deviation of the data set.
For the first part of the problem, we are required to find the probability that a randomly selected education major received a starting salary offer greater than $52,350. The formula to solve for the z-score is shown below:
z = (x - μ)/ σ
z = (52,350 - 46,292)/4,320
z = 1.4
The probability of the salary being greater than $52,350 can be found by using the Z-table or by using the formula P(Z > z) = 1 - P(Z < z). Here, P(Z < 1.4) = 0.9192
Therefore, P(Z > 1.4) = 1 - 0.9192 = 0.0808
For the second part of the problem, we are required to find the probability that a randomly selected education major received a starting salary offer between $45,000 and $52,350.
The formula to solve for the z-scores is shown below:
z1 = (45,000 - 46,292)/4,320z1 = -0.3z2 = (52,350 - 46,292)/4,320z2 = 1.4
The probability of the salary being between $45,000 and $52,350 can be found by using the formula
P(z1 < Z < z2) = P(Z < z2) - P(Z < z1).
Here, P(Z < -0.3) = 0.3821 and P(Z < 1.4) = 0.9192
Therefore, P(-0.3 < Z < 1.4) = 0.9192 - 0.3821 = 0.5371
To find the percentage of education majors that received a starting offer between $38,500 and $45,000, we first need to convert the values to z-scores. The formula to solve for the z-scores is shown below:
z1 = (38,500 - 46,292)/4,320
z1 = -1.8z2 = (45,000 - 46,292)/4,320
z2 = -0.3
The probability of the salary being between $38,500 and $45,000 can be found by using the formula P(z1 < Z < z2) = P(Z < z2) - P(Z < z1). Here, P(Z < -1.8) = 0.0359 and P(Z < -0.3) = 0.3821
Therefore, P(-1.8 < Z < -0.3) = 0.3821 - 0.0359 = 0.3462
Converting this probability to a percentage, we get:0.3462 x 100% = 34.62%
Therefore, the answer is d. 34.62%.
Therefore, the probability that a randomly selected education major received a starting salary offer greater than $52,350 is 0.0808. The probability that a randomly selected education major received a starting salary offer between $45,000 and $52,350 is 0.5371. The percentage of education majors that received a starting offer between $38,500 and $45,000 is 34.62%.Twenty percent of education majors were offered a starting salary less than 41,969.2$.
To know more about z-score visit:
brainly.com/question/31871890
#SPJ11