Answers
Answer:
2nd Option
Step-by-step explanation:
m=6
y=-3
so from equation
y=mx+c
y=6x-3
is the req ...... equation..
Answer: 2nd Option is the answer for this
Step-by-step explanation:
Related Questions
Help! “Ms.Day drew a rectangle on the board with a width of 14 cm and a digo al length of 50 cm. Find the length of this rectangle in centimeters.”

Answers
Answer:
length=48cm
Step-by-step explanation:
a²+14²=50²
a²+196=2500
a²=2304
a=48
Problem 2. Show that a damped harmonic oscillator ä + ax +w²x = 0 can be described by a Lagrangian.
Answers
The Lagrangian for a damped harmonic oscillator is given by L = (1/2) * m * (dx/dt)² - (1/2) * w² * x².
To show that a damped harmonic oscillator can be described by a Lagrangian, we need to derive the Lagrangian function for the system.
Let's consider a one-dimensional damped harmonic oscillator with position x(t) and damping coefficient a. The equation of motion for this system is given by:
m * ä + a * ä + w² * x = 0,
where m is the mass of the oscillator and w is the angular frequency.
We can rewrite the above equation as:
( m + a ) * ä + w² * x = 0.
Now, let's define the Lagrangian function L as the kinetic energy minus the potential energy:
L = T - V,
where T is the kinetic energy and V is the potential energy.
The kinetic energy T is given by:
T = (1/2) * m * v²,
where v = dx/dt is the velocity of the oscillator.
The potential energy V is given by:
V = (1/2) * w² * x².
Now, we can calculate the Lagrangian function:
L = T - V = (1/2) * m * v² - (1/2) * w² * x².
Next, we need to express the Lagrangian in terms of the generalized coordinates and their derivatives. In this case, the generalized coordinate is the position x.
The derivative of the position with respect to time is:
v = dx/dt.
Substituting this into the Lagrangian, we have:
L = (1/2) * m * (dx/dt)² - (1/2) * w² * x².
Now, let's calculate the Euler-Lagrange equation:
d/dt * (∂L/∂(dx/dt)) - ∂L/∂x = 0.
Taking the derivatives, we have:
d/dt * (m * (dx/dt)) - (-w² * x) = 0,
m * d²x/dt² + w² * x = 0,
which is the equation of motion for the damped harmonic oscillator.
Therefore, we have shown that the damped harmonic oscillator can be described by a Lagrangian, given by:
L = (1/2) * m * (dx/dt)² - (1/2) * w² * x².
To know more about Lagrangian, refer here:
https://brainly.com/question/32584067
#SPJ4
If I was to sketch the graph of y=4x+2
What would the graph look like?
Would it be a straight line or a curved line?
Where would it cross the y-axis?
What does 4 in 4x tell us?
Answers
Answer:
see explanation
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = 4x + 2 ← is in slope- intercept form
Thus its graph is a straight line
crosses the y- axis at (0, 2 ) , that is c = 2
the 4 in 4x is the slope m of the line
please help with all of question 5

Answers
Volume of a right cone with base radius r cm and height h cm :
V = 1/3 π r² h cm³
Surface area :
A = (π r² + π r √(h² + r²)) cm²
Volume of a sphere with radius r cm :
V = 4/3 π r³ cm³
Surface area :
A = 4 π r² cm²
Volume of a cuboid with dimensions r cm × r cm × h cm :
V = r² h cm³
Surface area :
A = 2 r² + 4 r h
a. If the cone and sphere have the same volume, then
1/3 π r² h = 4/3 π r³ ⇒ h = 4r
b. If the area of the cuboid is 98 cm², then
2 r² + 4 r h = 98 ⇒ r (r + 2 h) = 49
c. Since h = 4r, substituting this into the equation from (b) gives
r (r + 8 r) = 9 r² = 49 ⇒ r² = 49/9 ⇒ r = 7/3
d. With r = 7/3, we have
h = 4 × 7/3 = 28/3
and so the volume of the cuboid is
V = (7/3 cm)² (28/3 cm) = 1372/27 cm³
A construction crew has just built a new road. They built the road at a rate of 3 kilometers per week. They built 18.75 kilometers of road. How many weeks did
it take them?
Answers
Answer:
6.25 weeks
Step-by-step explanation:
Take 18.75 and divide it by 3, since the crew is finishing 3 km per week. You get 6.25, so it took the crew 6.25 weeks to finish the road.
Hopefully this helps- let me know if you have any questions!
according to the usgs, how much total copper was contained in world reserves as of 2018?(1 point)
Answers
According to the US Geological Survey (USGS), the total copper contained in world reserves as of 2018 was estimated to be approximately 830 million metric tons.
The USGS gathers and analyzes data on global mineral reserves, including copper. In their 2018 report, they estimated that the total identified copper resources worldwide were approximately 2.2 billion metric tons. However, not all of these resources are economically recoverable. To determine the amount of copper in world reserves, the USGS considers factors such as geology, mining methods, and economic viability.
Based on their analysis, the USGS estimated that around 38% of the identified copper resources were classified as reserves in 2018. Therefore, the calculated amount of copper in world reserves was approximately 830 million metric tons (2.2 billion metric tons x 38%).
In 2018, the USGS estimated that the world's copper reserves contained approximately 830 million metric tons. It is important to note that these estimates are subject to change as new discoveries are made, mining technologies evolve, and economic factors fluctuate. The USGS plays a crucial role in providing reliable and up-to-date information on global mineral resources to aid in resource planning and decision-making.
To know more about global mineral reserves, visit;
https://brainly.com/question/2109497
#SPJ11
Can someone help me please

Answers
Answer:
\(a_{n} = 12 -3(n-1)\)
Step-by-step explanation:
\(a_{1} = 12\\a_{n} = a_{n-1} - 3\)
we have to find formula for nth term of series for this problem
\(a_{1} = 12\\a_{2} = a_{2-1} - 3 = a_{1} -3 = 12 -3 = 9\\a_{3} = a_{3-1} - 3 = a_{2} -3 = 9 -3 = 6\)
Thus, we see series is 12, 9 ,6
Thus, we can see that series is decreasing by unit of 3.
and we know that when there is in increase or decrease in series by a a constant number then series is arithmetic progression series.
Hence, this is a decreasing AP series
In AP
nth term is given
nth term = a+(n-1)d
where a is the first term
d is the common difference
common difference is given by = nth term - (n-)th term
lets take 2nd and 1st term to get common difference.
d = 9-12 = -3
(note: this was obvious by looking at series itself that d is -3 as series was decreasing by 3 unit)
a = 12
thus, nth term = a +(n-1)d
nth term = 12 +(n-1)(-3)
nth term = 12 -3(n-1)
writing this in form of \(a_{n}\)
\(a_{n} = 12 -3(n-1)\) Answer
Of the mathematics graduates of a university, 40% received a starting salary of $60,000 or more. If 7 of the graduates are selected at random, find the probability that all had a starting salary of $60,000 or more
Answers
The probability that all 7 graduates selected at random received a starting salary of $60,000 or more is , 0.0065
This is a binomial probability problem where we have a sample of size 7 and want to find the probability that all 7 graduates received a starting salary of $60,000 or more.
We know that 40% of mathematics graduates received a starting salary of $60,000 or more,
So, the probability of any one graduate receiving a salary of $60,000 or more is 0.4.
Using the binomial probability formula, we can calculate the probability as follows:
P(X = 7) = (n choose X) pˣ (1-p)ⁿ⁻ˣ
where n is the sample size, x is the number of graduates who received a starting salary of $60,000 or more, p is the probability of success (i.e., receiving a salary of $60,000 or more), and (n choose X) is the number of ways to select X graduates out of n.
So in this case, we have:
n = 7, X = 7 and p = 0.4
Plugging into the formula, we get:
P(X = 7) = (7 choose 7) 0.4⁷ (1-0.4)⁷⁻⁷
P(X = 7) = (1) 0.4⁷ (0.6)⁰
P(X = 7) = 0.0065
Therefore, the probability that all 7 graduates selected at random received a starting salary of $60,000 or more is , 0.0065
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ4
a garrison has provision for 30 days for certain men. if 2/3 of them do not attend the mess, then the food will last for? (b) 65 days (d) none of
Answers
A garrison has provision for 30 days for certain men. if 2/3 of them do not attend the mess, then the food will last for 45 days. So, the correct option is (a).
How to calculateGiven that the provision for certain men in the garrison is for 30 days. Also, given that 2/3 of them do not attend the mess, then we have to find the number of days the food will last.
The food will last longer if the number of people attending the mess is less because the same amount of food will have to be shared between fewer people. Therefore, the food will last for more than 30 days.
Let the total number of men be x, then the number of men attending the mess is (1/3)x
And the number of men not attending the mess is (2/3)x.
Therefore, the food will last for (30 × x) / (2/3)x = 45 days
Hence, the answer of the question is 46 days.
Your question is incomplete but most probably your full question was:
A garrison has provision for 30 days for certain men. if 2/3 of them do not attend the mess, then the food will last for?
(a) 45 days
(b) 65 days
(c) 50 days
(d) none of above
Learn more about fraction at
https://brainly.com/question/10354322
#SPJ11
use calculator to find both the compound amount and the interest on $7000 at 12% for 2 years. Interest is compounded quarterly. what is compound amount? round to the nearest cent as needed what is the Interest? Round to the nearest cent as needed
Answers
Compound amount = $8867.39
compound interest = $1867.39
EXPLANATION
Given:
Principal(p) = $7000 Rate(r) = 0.12 Time(t) = 2 n= 4
We can calculate the compound amount(A) using the formula below:
\(A=P(1+\frac{r}{n})^{nt}\)Substitute the values and evaluate.
\(A=7000(1+\frac{0.12}{4})^{4\times2}\)\(=7000(1+0.03)^8\)\(=7000(1.03)^8\)\(\approx8867.39\)Hence, the compound amount = $8867.39
We proceed to find the compound interest.
A = P + I
⇒ I = A - P
= 8867.39 - 7000
=1867. 39
Therefore, the compound interest = $1867.39
please help me !!!!!!


Answers
The equation representing total fraction strip is ³/₃ + ¹/₃ = ⁴/₃.
option B.
What is a fraction?
A fraction is a mathematical representation of a part of a whole or a ratio between two numbers. It consists of a numerator, which represents the number of parts being considered, and a denominator, which represents the total number of parts in the whole.
For this case, 1 is divided into, and 1 divide into 3.
To obtain the total fractions, we will add the individual fractions as shown below;
For this first fraction = ¹/₃ + ¹/₃ + ¹/₃
For the second fraction = ¹/₃
Total fraction = 3(¹/₃ + ¹/₃ + ¹/₃) + ¹/₃
Total fraction = ³/₃ + ¹/₃ = ⁴/₃
Learn more about total fraction here: https://brainly.com/question/28699958
#SPJ1
What is the image of (-4,9) after a dialation by a scale factor of 3 centered at the origin
Answers
Answer:
-12,27
Step-by-step explanation:
Could someone help me please

Answers
Answer:
the answer should be 30
Step-by-step explanation:
since you can divided 15 by 5 to get 3, you can multiply 10 x 3 to get 30
radon has a cup of quarters and dimes with a total value of $4.90. the number of quarters is two less than two times the number of dimes. how many quarters and how many dimes does brandon have?
Answers
Using the Algebra operation,
Radon have 2 dimes and 2 quaters .
We have given that,
Radon has a cup of quarters and dimes .
total value of dimes and quaters = $4.90
let total number of quarters and number of dimes be x and y respectively.
numbers of quaters are 2 less than 2 times the number of dimes
i.e., x = 2y - 2 ---(1)
total values of quaters and dimes in dollars
=> y/10 + 25x/6 = $4.90
from equation (1) put value of x in equation 2
=> y/10 + 25 ( 2y-2)/6 = $4.90
=> y/10 + 50y/6 - 50/6 = 4.90
=> 253y/30 = 4.90 + 50/6 = 13.233
=> 253y = 397 => y = 1.6 ~ 2
put this value in equation (1)
=> x = 2×2 -2 = 2
Hence, randon has 2 dimes and 2 quaters .
To learn more about Algebra operation, refer :
https://brainly.com/question/24935016
#SPJ4
Complete the statement about this graph.765332.х553-3-2-11 2-1--2-3The zeros of the function of the graph lie atand the function is
Answers
The zeros of the function of the graph lies at 0 and 2.
And the function of the graph is a polynomial of degree 4.
The streptococci bacteria population N at time t (in months) is given by N = N0e 2t where N0 is the initial population. If the initial population was 100, how long does it take for the population to reach one million?
Answers
PLS ASAP AND TY IF U ANSWERED

Answers
Answer:
3.5 un
Step-by-step explanation:
to find the new length of the square using a scale factor of 1/7 you can just multiply 24.5 by 1/7
this is basically dividing 24.5 by 7
24.5 / 7 = 3.5
that is your answer
easy one for you folks.

Answers
Answer:
if its easy do it
Step-by-step explanation:
Answer:
7.5/15 or something because yes
A mother has two apples, three pears, and four oranges. She plans to give her son one piece of fruit every morning for nine days. How many ways are there to do this?
Answers
Answer:
Umm nine ways?
Step-by-step explanation:
Answer:
1260
Step-by-step explanation:
35x36
Which function description matches the transformation on the graph?

Answers
Answer:
g(x)=f(x+6)
Step-by-step explanation:
it was translated backward by 6 units
Write the slope intercept form of x+3y=4
Answers
Answer:
y=-1/3x + 4/3
Step-by-step explanation:
factories
Need fast
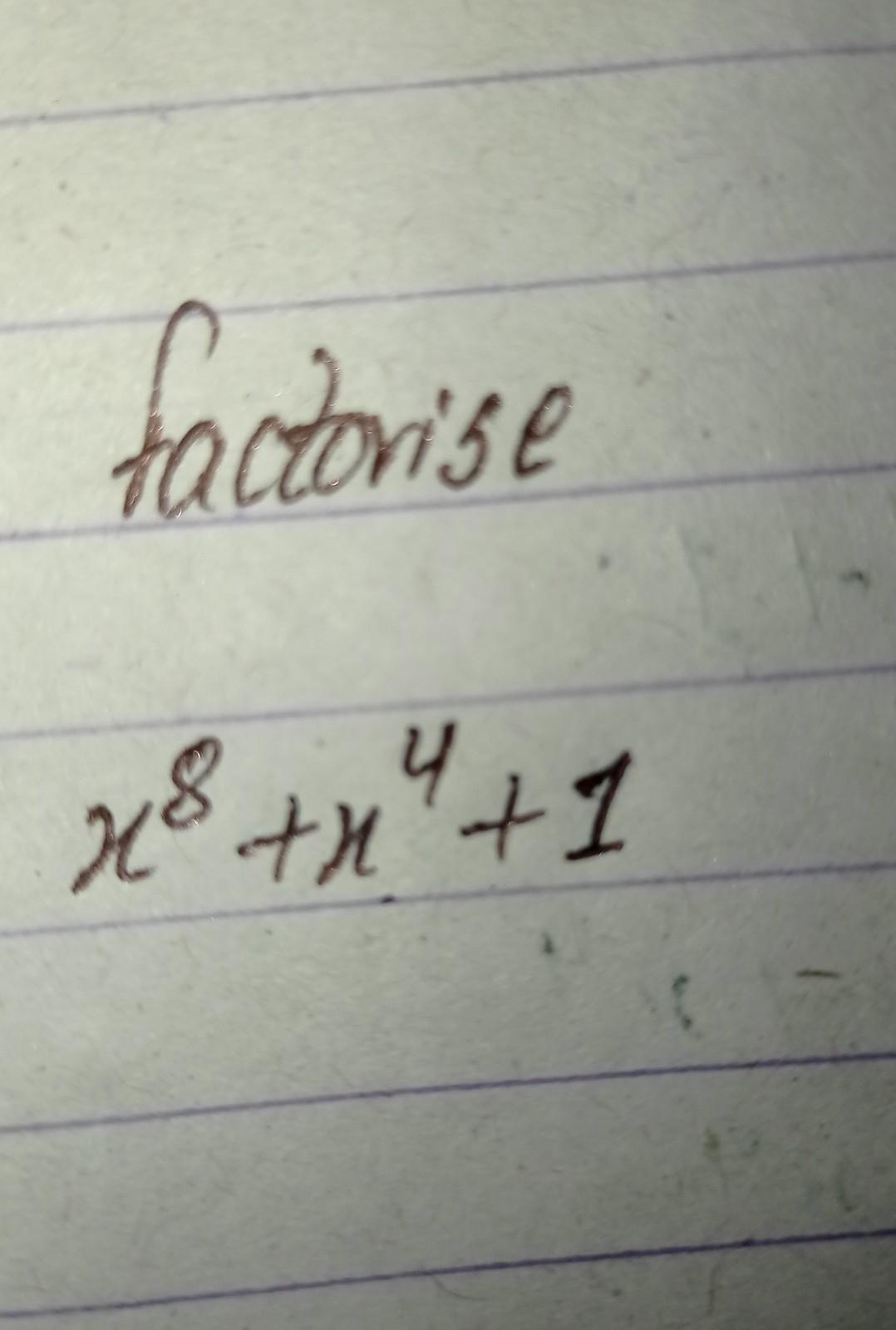
Answers
Factor x^8+x^4+1
Rewrite the middle term.
X^8+2x^4.1-x^4+1
Rearrange terms.
x^8+2x^4.1+1 -x^4
Factor first three terms by perfect square rule
(X^4+1)^2-x^4
Rewrite
x^4
as
(X^2)^2
(X^4+1)-(x^2)^2
Since both terms are perfect squares, factor using the difference of squares formula,
a^2-b^2=(a+b)(a-b)
where
a=x^4+1
and
b=x^2
Simplify.
(X^4+1+x^2)(x^4+1-x^2)
Step-by-step explanation:
Have a great day
\( {x}^{8} + {x}^{4} + 1\)
to find:factorise
solution:\( {x}^{8} + {x}^{4} + 1\)
\( = x ^{8} + 2 {x}^{4} + 1 - {x}^{4} \)
\( = ( {x}^{4} + 1 {)}^{2} - ( {x}^{2} {)}^{2} \)
\( = ({x}^{4 } + 1 + {x}^{2}) ( {x}^{4} + 1 - {x}^{2} )\)
\( = ( {x}^{4} + 2 {x}^{2} + 1 - {x}^{2} )( {x}^{4} - {x}^{2} + 1)\)
\( = (( {x}^{2} + 1 {)}^{2} - {x}^{2} )( {x}^{4} - {x}^{2} + 1)\)
\( = ( {x}^{2} + 1 + x)( {x}^{2} + 1 - x)\)
\( = ( {x}^{4} - {x}^{2} + 1)\)
can someone help me ill mark you brainliest

Answers
Answer:
Equation: x+x+6=20
x=7
Andy completed 16 problems
Step-by-step explanation:
y = 2x + 3
y=2x-1
The system has how many solutions?
one solution
two solutions
no solution
an infinite number of solutions
Answers
A tank contains 180 gallons of water and 15 oz of salt. water containing a salt concentration of 17(1+15sint) oz/gal flows into the tank at a rate of 8 gal/min, and the mixture in the tank flows out at the same rate.
the long-time behavior of the solution is an oscillation about a certain constant level. what is this level? what is the amplitude of the oscillation?
Answers
Let A(t) denote the amount of salt (in ounces, oz) in the tank at time t (in minutes, min).
Salt flows in at a rate of
\(\dfrac{dA}{dt}_{\rm in} = \left(17 (1 + 15 \sin(t)) \dfrac{\rm oz}{\rm gal}\right) \left(8\dfrac{\rm gal}{\rm min}\right) = 136 (1 + 15 \sin(t)) \dfrac{\rm oz}{\min}\)
and flows out at a rate of
\(\dfrac{dA}{dt}_{\rm out} = \left(\dfrac{A(t) \, \mathrm{oz}}{180 \,\mathrm{gal} + \left(8\frac{\rm gal}{\rm min} - 8\frac{\rm gal}{\rm min}\right) (t \, \mathrm{min})}\right) \left(8 \dfrac{\rm gal}{\rm min}\right) = \dfrac{A(t)}{180} \dfrac{\rm oz}{\rm min}\)
so that the net rate of change in the amount of salt in the tank is given by the linear differential equation
\(\dfrac{dA}{dt} = \dfrac{dA}{dt}_{\rm in} - \dfrac{dA}{dt}_{\rm out} \iff \dfrac{dA}{dt} + \dfrac{A(t)}{180} = 136 (1 + 15 \sin(t))\)
Multiply both sides by the integrating factor, \(e^{t/180}\), and rewrite the left side as the derivative of a product.
\(e^{t/180} \dfrac{dA}{dt} + e^{t/180} \dfrac{A(t)}{180} = 136 e^{t/180} (1 + 15 \sin(t))\)
\(\dfrac d{dt}\left[e^{t/180} A(t)\right] = 136 e^{t/180} (1 + 15 \sin(t))\)
Integrate both sides with respect to t (integrate the right side by parts):
\(\displaystyle \int \frac d{dt}\left[e^{t/180} A(t)\right] \, dt = 136 \int e^{t/180} (1 + 15 \sin(t)) \, dt\)
\(\displaystyle e^{t/180} A(t) = \left(24,480 - \frac{66,096,000}{32,401} \cos(t) + \frac{367,200}{32,401} \sin(t)\right) e^{t/180} + C\)
Solve for A(t) :
\(\displaystyle A(t) = 24,480 - \frac{66,096,000}{32,401} \cos(t) + \frac{367,200}{32,401} \sin(t) + C e^{-t/180}\)
The tank starts with A(0) = 15 oz of salt; use this to solve for the constant C.
\(\displaystyle 15 = 24,480 - \frac{66,096,000}{32,401} + C \implies C = -\dfrac{726,594,465}{32,401}\)
So,
\(\displaystyle A(t) = 24,480 - \frac{66,096,000}{32,401} \cos(t) + \frac{367,200}{32,401} \sin(t) - \frac{726,594,465}{32,401} e^{-t/180}\)
Recall the angle-sum identity for cosine:
\(R \cos(x-\theta) = R \cos(\theta) \cos(x) + R \sin(\theta) \sin(x)\)
so that we can condense the trigonometric terms in A(t). Solve for R and θ :
\(R \cos(\theta) = -\dfrac{66,096,000}{32,401}\)
\(R \sin(\theta) = \dfrac{367,200}{32,401}\)
Recall the Pythagorean identity and definition of tangent,
\(\cos^2(x) + \sin^2(x) = 1\)
\(\tan(x) = \dfrac{\sin(x)}{\cos(x)}\)
Then
\(R^2 \cos^2(\theta) + R^2 \sin^2(\theta) = R^2 = \dfrac{134,835,840,000}{32,401} \implies R = \dfrac{367,200}{\sqrt{32,401}}\)
and
\(\dfrac{R \sin(\theta)}{R \cos(\theta)} = \tan(\theta) = -\dfrac{367,200}{66,096,000} = -\dfrac1{180} \\\\ \implies \theta = -\tan^{-1}\left(\dfrac1{180}\right) = -\cot^{-1}(180)\)
so we can rewrite A(t) as
\(\displaystyle A(t) = 24,480 + \frac{367,200}{\sqrt{32,401}} \cos\left(t + \cot^{-1}(180)\right) - \frac{726,594,465}{32,401} e^{-t/180}\)
As t goes to infinity, the exponential term will converge to zero. Meanwhile the cosine term will oscillate between -1 and 1, so that A(t) will oscillate about the constant level of 24,480 oz between the extreme values of
\(24,480 - \dfrac{267,200}{\sqrt{32,401}} \approx 22,995.6 \,\mathrm{oz}\)
and
\(24,480 + \dfrac{267,200}{\sqrt{32,401}} \approx 25,964.4 \,\mathrm{oz}\)
which is to say, with amplitude
\(2 \times \dfrac{267,200}{\sqrt{32,401}} \approx \mathbf{2,968.84 \,oz}\)
Find f/(x). (a) f(x) = xsinx (b) f(x) = sech-1x²
Answers
The derivative of f(x) = sech^(-1)(x^2) is f'(x) = 2x/sqrt(1 - x^4).
a) To find f'(x) for f(x) = x*sin(x), we can use the product rule and the derivative of the sine function.
Using the product rule, we have:
f'(x) = (xsin(x))' = xsin'(x) + sin(x)*x'
The derivative of sin(x) is cos(x), and the derivative of x with respect to x is 1. Therefore:
f'(x) = x*cos(x) + sin(x)
So, the derivative of f(x) = xsin(x) is f'(x) = xcos(x) + sin(x).
(b) To find f'(x) for f(x) = sech^(-1)(x^2), we can use the chain rule and the derivative of the inverse hyperbolic secant function.
Let u = x^2. Then, f(x) can be rewritten as f(u) = sech^(-1)(u).
Using the chain rule, we have:
f'(x) = f'(u) * u'
The derivative of sech^(-1)(u) can be found using the derivative of the inverse hyperbolic secant function:
(sech^(-1)(u))' = 1/sqrt(1 - u^2)
Since u = x^2, we have:
f'(x) = 1/sqrt(1 - (x^2)^2) * (x^2)'
Simplifying:
f'(x) = 1/sqrt(1 - x^4) * 2x
So, the derivative of f(x) = sech^(-1)(x^2) is f'(x) = 2x/sqrt(1 - x^4).
learn more about derivative here
https://brainly.com/question/29144258
#SPJ11
help me please!!!!!!!

Answers
Answer:
C
Step-by-step explanation:
It's C because i majored in mathmatics in college and ended with a A
A system of two linear equations is graphed. The lines have the same slope, but different intercepts. How many solutions does the system have?. A. 0. B. 1. C. 2. D. infinite
Answers
Answer:
D
Step-by-step explanation:
I hope this is correct and have a great day
g(x) = x3 + 6x2 + 12x + 8
A 2-column table with 5 rows. The first column is labeled g of x with entries negative 3, negative 2, 0, 2, 3. The second column is labeled f of x with entries negative 1, 0, 8, 64, 125.
Determine the function’s value when x = −1.
Answers
The value of the function g(x) = x^3 + 6x^2 + 12x + 8 when x = -1 is 1
How to evaluate the function?The equation of the function is given as:
g(x) = x^3 + 6x^2 + 12x + 8
When x = -1, we have:
g(-1) = (-1)^3 + 6(-1)^2 + 12(-1) + 8
Evaluate the expression
g(-1) = 1
Hence, the value of the function g(x) = x^3 + 6x^2 + 12x + 8 when x = -1 is 1
Read more about functions at:
https://brainly.com/question/4025726
#SPJ1
Answer:
g(-1) = 1
Step-by-step explanation:
Dani's neighbors paid her to take care of their bird during their vacation. Dani spent $4 of her earnings on an afternoon snack and $16 on a new book. Afterward, she had at least $8 left. Complete the inequality below to represent how much Dani's neighbors paid her.
Answers
Answer: Her neighbors paid her 28 dollars
Step-by-step explanation: if you add 4, 16, and 8 then you get 28
