I need help fast please I don’t understand this and I’ve been struggling for a while. Can I get a brain list please or a tutor to answer this.

Answers
Answer:
4 √6
Step-by-step explanation:
We have a few right triangles. We know that a²+b²=c², with c being the side opposite the right angle. Representing the side without a value as z, we have:
m²+z² = (8+4)² = 12²
4²+n²=z²
8²+n²=m²
We have 3 equations with 3 unknown variables, so this should be solvable. One way to find a solution is to put everything in terms of m and go from there. First, we can take n out of the equations entirely, removing one variable. We can do this by solving for it in terms of z and plugging that into the third equation, removing a variable as well as an equation.
4²+n²=z²
subtract 4²=16 from both sides
z²-16 = n²
plug that into the third equation
64 + z² - 16 = m²
48 + z² = m²
subtract 48 from both sides to solve for z²
z² = m² - 48
plug that into the first equation
m² + m² - 48 = 144
2m² - 48 = 144
add 48 to both sides to isolate the m² and its coefficient
192 = 2m²
divide both sides by 2 to isolate the m²
96 = m²
square root both sides to solve for m
√96 = m
we know that 96 = 16 * 6, and 16 = 4², so
m = √96 = √(4²*6) = 4 √6
Related Questions
Sketch the graph of the line.x + y = -5
Answers
The given line is
\(x+y=-5\)We need two points to graph a line. Let's find the axis intercepts with x=0 and y=0.
The y-intercept: x=0
\(\begin{gathered} 0+y=-5 \\ y=-5 \end{gathered}\)The y-intercept is (0,-5).
The x-intercept: y=0
\(\begin{gathered} x+0=-5 \\ x=-5 \end{gathered}\)The x-intercept is (-5,0).
Now, we graph these points and draw a straight line.

Convert the given polar equation to a Cartesian equation. (Use the following as necessary: x and y.)
r = 4 / sin(θ) + 5 cos(θ)
Answers
The Cartesian equation will be;
⇒ x² + y² - 4x - 5y = 0
What is an expression?
Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The polar equation will be;
⇒ r = 4 sin(θ) + 5 cos(θ)
Now,
Substitute r = √x² + y² , r sin θ = x, r cos θ = y in above equation, we get;
The polar equation will be;
⇒ r = 4 sin(θ) + 5 cos(θ)
⇒ r² = 4 r sin(θ) + 5 r cos(θ)
⇒ x² + y² = 4x + 5y
⇒ x² + y² - 4x - 5y = 0
Thus, The Cartesian equation will be;
⇒ x² + y² - 4x - 5y = 0
Learn more about the polar form visit:
https://brainly.com/question/16166662
#SPJ1
MATH PLEASE DO THIS FOR BRAINLYIST

Answers
Answer: The percent of change in the perimeter is 100 percent and
the percent of change in the area is 300 percent .
Step-by-step explanation:
Rectangle is the closed shaped polygon with 4 sides. Opposite sides of the rectangle are equal. when the length and the width of the sandbox are doubled the percent of change in the perimeter is 100 percent and the percent of change in the area is 300 percent.
Help math almost done thank pleas

Answers
Hey there! :)
2^6 means 2*2*2*2*2*2 = 64
5^2 means 5*5 = 25
64*25=1,600
If it is correct, plss mark Brainliest
Infinity please..
let y1, . . . , yn iid∼ f(y). find the sampling distribution of: y(1) = min i yi
Answers
A modified version of the original distribution, the sampling distributive of y(1) has an upper bound equal to the minimum value in the sample and a lower bound of 0.
Let y1,..., yn have an f-distribution and be independently and identically distributed (iid) (y).
Ascertain the y(1) = min I yi sampling distribution. The sampling distribution of y(1) has a lower bound of 0 and an upper bound that is equal to the minimum of the sample yi. It is a truncated distribution of the original distribution f(y).
By integrating the initial distribution f(y) from 0 to the minimum of the sample yi, get the probability of each value of y(1).
A reduced version of the original distribution f(y), with a lower bound of 0 and an upper bound equal to the minimum of the sample yi, is the sampling distribution of y(1). We must integrate the initial distribution f in order to calculate this distribution (y)
Learn more about distributive here
https://brainly.com/question/5637942
#SPJ4
the water side of the wall of a 70-m-long dam is a quarter circle with a radius of 7 m. determine the hydrostatic force on the dam and its line of action when the dam is filled to the rim.
Answers
The hydrostatic force on the dam is 2,641,100 N and the line of action is 2.625 m.
The hydrostatic force on the dam and its line of action when the dam is filled to the rim can be calculated by using the given information. The water side of the wall of a 70-m-long dam is a quarter circle with a radius of 7 m.
In order to determine the hydrostatic force on the dam and its line of action when the dam is filled to the rim, we can follow the below steps:
Step 1: Calculate the area of the quarter circle. The area of the quarter circle is given by; A = πr²/4 = (22/7) × 7 × 7 / 4 = 38.5 m²
Step 2: Calculate the depth of water- The depth of the water is equal to the radius of the quarter circle. The depth of water is;d = r = 7 m
Step 3: Calculate the hydrostatic pressure- The hydrostatic pressure can be calculated using the formula; P = ρgdwhere,P = Hydrostatic pressureρ = density of water (1000 kg/m³)g = gravitational acceleration (9.8 m/s²)d = depth of the water (7 m)
On substituting the given values in the above formula, we get;P = 1000 × 9.8 × 7 = 68600 N/m²
Step 4: Calculate the hydrostatic force The hydrostatic force on the dam is given by; F = PA where, A = area of the quarter circle (38.5 m²)P = hydrostatic pressure (68600 N/m²)On substituting the given values in the above formula, we get; F = 68600 × 38.5 = 2641100 N
Step 5: Calculate the line of action of hydrostatic force The line of action of the hydrostatic force is given by; h = 3r/8 = 3 × 7 / 8 = 2.625 m .
Therefore, the hydrostatic force on the dam is 2,641,100 N and the line of action is 2.625 m.
To know more about Hydrostatic pressure, refer here:
https://brainly.com/question/28206120#
#SPJ11
parameterize the plane that contains the three points (−4,−1,4), (−6,−8,8), and (50,20,15). r→(s,t)=
Answers
For the parameterize plane that contains the three points (−4,−1,4), (−6,−8,8), and (50,20,15) the value of r→(s,t) is (-4 + 2s - 25t, -1 + 7s - 82t, 4 - 4s + 87t).
To parameterize the plane that contains the three points (-4, -1, 4), (-6, -8, 8), and (50, 20, 15), we can use the method of finding two vectors in the plane and then taking their cross product. Let's call the parameterized form r→(s,t) = (x(s, t), y(s, t), z(s, t)).
Step 1: Find two vectors in the plane.
Let's consider the vectors formed by the given points:
v1 = (-4, -1, 4) - (-6, -8, 8) = (2, 7, -4)
v2 = (-4, -1, 4) - (50, 20, 15) = (-54, -21, -11)
Step 2: Take the cross product of the two vectors.
n = v1 × v2
Using the cross-product formula, we have:
n = (7 × (-11) - (-4) × (-21), (-4) × (-54) - (2) × (-11), (2) × (-21) - 7 × (-54))
= (-25, -82, 87)
Step 3: Parameterize the plane using the normal vector.
Now, we can use the normal vector (the result from step 2) to parameterize the plane:
r→(s,t) = (-4, -1, 4) + s(2, 7, -4) + t(-25, -82, 87)
Therefore, the parameterized form of the plane that contains the three points is:
r→(s,t) = (-4 + 2s - 25t, -1 + 7s - 82t, 4 - 4s + 87t)
Learn more about the parameterization of planes at
https://brainly.com/question/28740237
#SPJ4
Triangle properties

Answers
All sum up to 180
Then less 115 from it to get your x
find the equation of the locus of a point is at a distance 7 units from the point(1,6).
Answers
Answer:
Step-by-step explanation:
let (x,y) be any point on the locus.
Then
\(\sqrt{(x-1)^2+(y-6)^2} =7\\or\\(x-1)^2+(y-6)^2=49\\which ~is~a~circle.\)
Work out the perimeter of a rectangle with length 7. 7cm and width 8. 1cm.
Answers
The lengths of all the sides of a rectangle are added to determine its perimeter.
The perimeter of a rectangle with dimensions of 7.7 cm in length and 8.1 cm in breadth can be calculated as follows:
Perimeter is equal to 2 * (Length + Width).
If we substitute the values, we get:
Perimeter: (7.7 cm + 8.1 cm) x (2 *).
Radius = 2 * 15.8 cm
Measurement is 31.6 cm.
As a result, the rectangle's perimeter is 31.6 cm.
learn more about rectangle here :
https://brainly.com/question/15019502
#SPJ11
3. Kai Hayashi owns 60 shares of Comerica Inc. for which he
paid $3,945.90, including a commission of $113.40. Comerica
pays annual dividends of $1.92.
a. What was the cost per share?
b. What is the annual yield?
Answers
The Annual yield is approximately 2.92%.
To determine the cost per share and the annual yield, we need to perform some calculations based on the given information.
a. Cost per share:
The cost per share can be calculated by dividing the total cost (including the commission) by the number of shares.
Total cost = Cost of shares + Commission
Total cost = $3,945.90
Number of shares = 60
Cost per share = Total cost / Number of shares
Cost per share = $3,945.90 / 60
Cost per share ≈ $65.76
Therefore, the cost per share is approximately $65.76.
b. Annual yield:
The annual yield is the dividend per share divided by the cost per share, expressed as a percentage.
Dividend per share = $1.92
Annual yield = (Dividend per share / Cost per share) * 100
Annual yield = ($1.92 / $65.76) * 100
Annual yield ≈ 2.92%
Therefore, the annual yield is approximately 2.92%.
In summary:
a. The cost per share for Comerica Inc. is approximately $65.76.
b. The annual yield for Comerica Inc. is approximately 2.92%.
For more questions on Annual .
https://brainly.com/question/28990623
#SPJ8
X/5=y/3 and 12/y=4/5 what does x equal and what does y equal and how?
Answers
Final Answer: \(x = \frac{5y}{3}\), \(y = 15\)
Steps/Reasons/Explanation:
Question: \(\frac{x}{5} = \frac{y}{3}\) and \(\frac{12}{y} = \frac{4}{5}\). What does \(x\) equal and what does \(y\) equal and how?
Solving for \(x\) in the equation \(\frac{x}{5} = \frac{y}{3}\).
Step 1: Multiply both sides by \(5\).
\(x = \frac{y}{3} * 5\)
Step 2: Simplify \(\frac{y}{3} * 5\) to \(\frac{y * 5}{3}\).
\(x = \frac{y * 5}{3}\)
Step 3: Regroup terms.
\(x = \frac{5y}{3}\)
Solving for \(y\) in the equation \(\frac{12}{y} = \frac{4}{5}\).
Step 1: Multiply both sides by \(y\).
\(12 = \frac{4}{5}y\)
Step 2: Simplify \(\frac{4}{5}y\) to \(\frac{4y}{5}\).
\(12 = \frac{4y}{5}\)
Step 3: Multiply both sides by \(5\).
\(12 * 5 = 4y\)
Step 4: Simplify \(12 * 5\) to \(60\).
\(60 = 4y\)
Step 5: Divide both sides by \(4\).
\(\frac{60}{4} = y\)
Step 6: Simplify \(\frac{60}{4}\) to \(15\).
\(15 = y\)
Step 7: Switch sides.
\(y = 15\)
~I hope I helped you :)~
Matsu walks 2 blocks west from the police station and then walks 3 blocks north. Give the coordinates of the place where he stops
Answers
Let D be the region bounded below by the cone z = √√x² + y² and above by the sphere x² + y² +2²= 25. Then the z-limits of integration to find the volume of D, using rectangular coordinates an
Answers
The correct z-limits of integration to find the volume of the region D are given by option C, which is \(\sqrt{(x^{2} + y^{2} )} \leq z \leq \sqrt{25 - x^{2} - y^{2}}\).
To determine the z-limits of integration, we need to consider the bounds of the region D. The region is bounded below by the cone \(z=\sqrt{(x^{2} + y^{2} )}\) and above by the sphere \(x^{2} + y^{2} + z^{2} = 25\).
The lower bound is defined by the cone, which is given by \(z=\sqrt{(x^{2} + y^{2} )}\). This means that the z-coordinate starts at the value \(\sqrt{(x^{2} + y^{2} )}\) when we integrate over the region.
The upper bound is defined by the sphere, which is given by \(x^{2} + y^{2} + z^{2} = 25\). By rearranging the equation, we have \(z^{2} = 25 - x^{2} - y^{2}\). Taking the square root of both sides, we obtain \(z=\sqrt{25-x^{2} -y^{2} }\). This represents the maximum value of z within the region.
Therefore, the correct z-limits of integration are \(\sqrt{(x^{2} + y^{2} )} \leq z \leq \sqrt{25 - x^{2} - y^{2}}\), which corresponds to option C. This choice ensures that we consider all z-values within the region D when integrating in the order \(dzdydx\) to find its volume.
Learn more about integration here:
https://brainly.com/question/30217024
#SPJ11
The complete question is:
Let D be the region bounded below by the cone \(z=\sqrt{(x^{2} + y^{2} )}\) and above by the sphere \(x^{2} + y^{2} + z^{2} = 25\). Then the z-limits of integration to find the volume of D, using rectangular coordinates and taking the order of integration as \(dzdydx\) are:
A. \(25 - x^{2} - y^{2} \leq z \leq \sqrt{(x^{2} + y^{2} )}\)
B. \(\sqrt{(x^{2} + y^{2} )} \leq z \leq 25 - x^{2} - y^{2}\)
C. \(\sqrt{(x^{2} + y^{2} )} \leq z \leq \sqrt{25 - x^{2} - y^{2}}\)
D. None of these
What is the solution to the system of equations?
6x−4y=152
y=3x−762
Answers
Answer:
Hi! The correct answer is (1448/3, 686)
Step-by-step explanation:
~Solve for the first variable in one of the equations, then substitute the result into the other equation~
the sum of twice a
number and 31
Answers
Answer:
Let the unknown number be x ;
\(2(x) +31\\=2x+31\)
Step-by-step explanation:
–18 • –17
solve please
Answers
Answer:
306
Step-by-step explanation:
Answer:
306
Step-by-step explanation:
-18x-17 is 306 because a negative number times a negative number is always a positive so it would be 18x17 which is 306
help pkzzzzzzz
solve for x.
\( \frac{4}{5} x = - \frac{1}{4} \)
Answers
4/5x = -1/4
x = -1/4 × 5/4
x = -5/16
x = -0.3125
_____
RainbowSalt2222 ☔
In Exercises 3-4, use the Subspace Test to determine which of the sets are subspaces of Mnn 3. a. The set of all diagonal n × n matrices. b. The set of all n x n matrices A such that det(A) = 0. c. The set of all n x n matrices A such that tr(A) = 0. d. The set of all symmetric n x n matrices
Answers
The set of all diagonal n × n matrices is a subspace of Mnn3.
Given, we need to use the Subspace Test to determine which of the sets are subspaces of Mnn3 and the sets are: The set of all diagonal n × n matrices.
The set of all n x n matrices A such that det(A) = 0.The set of all n x n matrices A such that tr(A) = 0.The set of all symmetric n x n matrices.
Subspace Test: A nonempty subset H of a vector space V is a subspace of V if for every u and v in H and every scalar c, the vector cu + v is in H.
The set of all diagonal n × n matrices.Here, we have to prove that the set of all diagonal matrices is a subspace of Mnn3.
Let A and B be two diagonal matrices. Then, A + B is also a diagonal matrix. Since the diagonal elements of A + B are equal to the sums of the corresponding diagonal elements of A and B. So, the set of all diagonal matrices is closed under addition. Let A be a diagonal matrix and c be a scalar.
Then, cA is also a diagonal matrix. Since the diagonal elements of cA are equal to the product of c and corresponding diagonal elements of A. So, the set of all diagonal matrices is closed under scalar multiplication.
Therefore, the set of all diagonal matrices is a subspace of Mnn3. Hence, the main answer is: a. The set of all diagonal n × n matrices is a subspace of Mnn3.
We have used the subspace test to prove that the set of all diagonal n × n matrices is a subspace of Mnn3. The subspace test is used to verify whether a given subset of a vector space is a subspace or not.
We have proved that the set of all diagonal matrices is closed under addition and scalar multiplication.
The diagonal elements of A + B are equal to the sums of the corresponding diagonal elements of A and B. And the diagonal elements of cA are equal to the product of c and corresponding diagonal elements of A.
Therefore, the set of all diagonal matrices satisfies all the three properties required for a subset to be a subspace.
Hence, the set of all diagonal n × n matrices is a subspace of Mnn3.
In conclusion, we can say that the set of all diagonal n × n matrices is a subspace of Mnn3 as it satisfies the subspace test.
To know more about vector space visit:
brainly.com/question/31425895
#SPJ11
Given f(x) and g(x) = f(x) + k, look at the graph below and determine the value of k. (1 point) 92 fix)
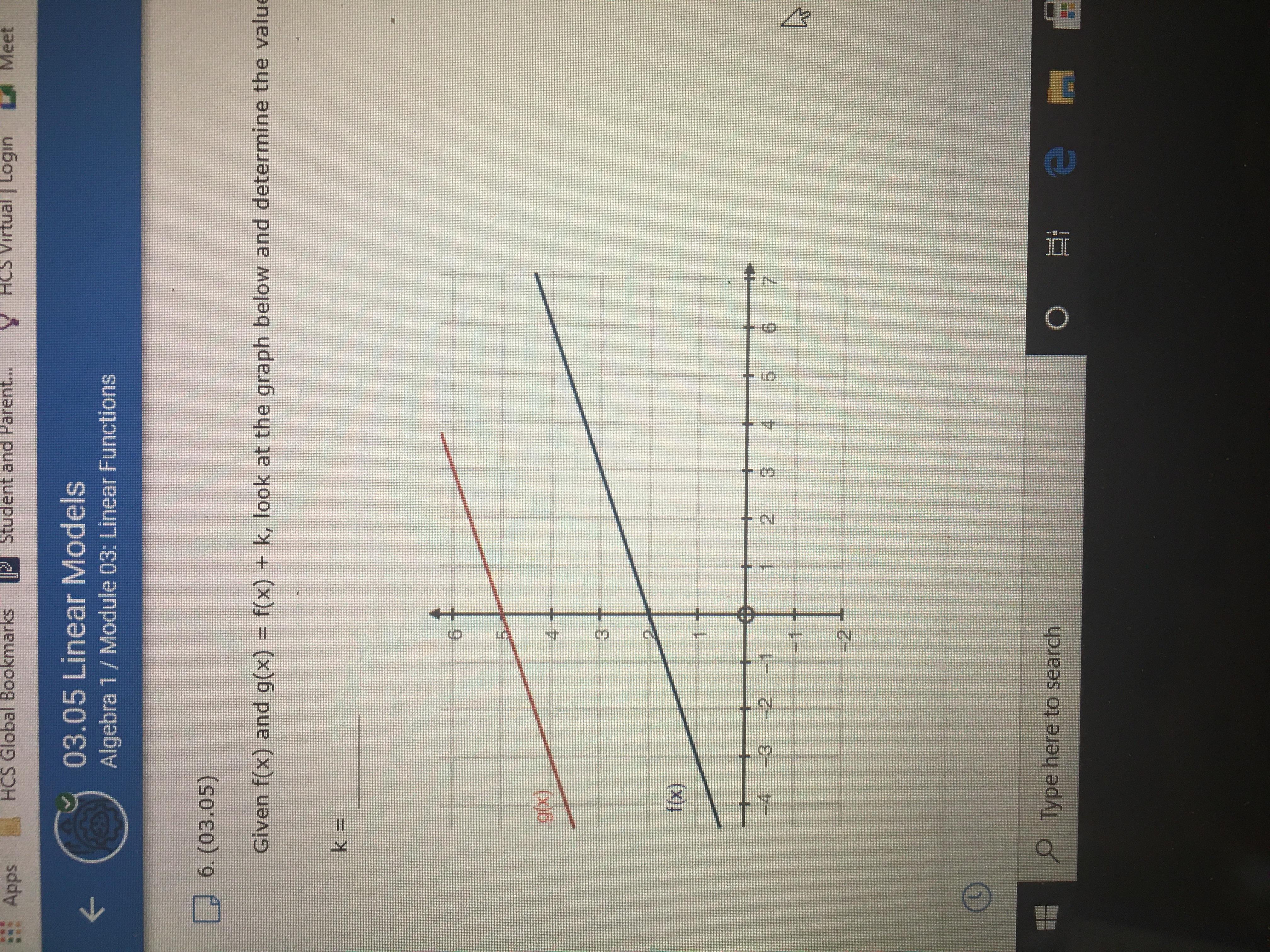
Answers
Answer:
3
Step-by-step explanation:
g(x) = f(x) + k, is true for all values of x.
At x = 0, f(x) = 2
At x = 0, g(x) = 5
Therefore, at x = 0
=> g(x) = f(x) + k
=> 5 = 2 + k
=> 3 = k
Since, the given relation is true for all real values of x, k is independent of x. Thus k = 3, for every value of x
Can someone plz help me plz I beg uuuu plz I will really appreciate it

Answers
Answer:
x=45
Step-by-step explanation:
(2x+10) + 30 + 50 = 180
2x+10+30+50 = 180
2x+90=180
2x=90
x-45
60° 60° y=? (geometry)

Answers
Answer:
Y=90°Step-by-step explanation:
You could tell because triangles like this always have a right angle (which is a 90° angle)
If there is a bisector in the middle of the triangle that is perpendicular to the base, then it will be a right angle
what is 140 divided by 8
Answers
Answer:
17.5
Step-by-step explanation:
Answer:
17.5 is your answer
Step-by-step explanation:
140/8
17.5
Hope this helps?
please help!!!!!!2!!!!!!!

Answers
Answer:
a.) 12 + x = < -8
b.) x + -8 > 12
c.) -8 - x < 12
Please help I have been stuck for a while

Answers
Answer:
B. 50 degrees
Step-by-step explanation:
I am not 100% sure and if this is a right triangle, then it's measure is 90 degrees. So, 140 degrees minus 90 degrees would total, 50 degrees.
Answer:
B: 50 degrees
Step-by-step explanation:
You first find the other angles of the triangle. One is 90 degrees at the corner. The other would be 40 because the outside angle is 140 and that is 40 away from 80. Add 40 and 90 together to get 130 degrees. Subtract that from 180 and that is 50 degrees :)
Hope this helps!
In a city, 49% of the adults are male. Of the adults, 24% are male and rent action-movie DVDs and 10% are female and rent action-movie DVDs.
If an adult is randomly picked, the probability that the person rents action-movie DVDs, given that the person is female, is
.
Answers
Answer:
I getting the probability of the adult female that will rent the action movies in DVDs in by dividing the possible probability outcome which is 10% of all adults by the total number of possible outcome. So all of the population of the female is 51% and the ones who rent is only 10%. the probability is 19%
The solution is, 0.20 is the probability that the person rents action-movie DVDs, given that the person is female.
What is probability?Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event.
here, we have,
given that,
Data:
A: the adult is a male, P(A) = 0.49
B: the adult rent action-movie DVDs
C: the adult is a female, P(C) = 1 - P(A) = 1 - 0.49 = 0.51
24% of the adults are male and rent action-movie DVDs, then P(A ∩ B) = 0.24
10% of the adults are female and rent action-movie DVDs, then P(C ∩ B) = 0.10
The conditional probability of B (the adult rents action-movie DVDs) given C (the adult is female) is computed as follows:
P(B|C) = P(C ∩ B)/P(C)
= 0.1/0.51
= 0.2
Hence, The solution is, 0.20 is the probability that the person rents action-movie DVDs, given that the person is female.
To learn more on probability click:
brainly.com/question/11234923
#SPJ7
Triangle ABC with vertices at A(−3, −3), B(3, 3), C(0, 3) is dilated to create triangle A′B′C′ with vertices at A′(−9, −9), B′(9, 9), C′(0, 9). Determine the scale factor used. 6 one sixth 3 one third
Answers
Answer:
3
Step-by-step explanation:
if you dilate a triangle and it gets bigger the answer is a whole number if it gets smaller it is a fraction
-3 X 3 =-9
3 X 3 =9
0 X 3 =0
dilated by 3
According to the Empirical Rule, approximately _____% of the data in a normal distribution will fall within ±1 standard deviation of the mean.
a. 34
b. 68
c. 95
d. 99.7
Answers
According to the Empirical Rule, approximately 68% of the data in a normal distribution will fall within ±1 standard deviation of the mean.
The correct option is (b)
Empirical Rule:The empirical rule states that the proportion of values within 1,2, and 3 standard deviations of the mean are approximately 68%, 95%, and 99.7% approximately. It implies majority of the values in a normal distribution lies within 1 standard deviations of the mean.
The Empirical Rule states that for a normal distribution:
About 68% of the data will fall within 1 standard deviation of the mean
About 95% of the data will fall within 2 standard deviations of the mean
About 99.7% of the data will fall within 3 standard deviations of the mean
Therefore, option (b) 68 is the correct answer.
Learn more about Standard deviation at:
https://brainly.com/question/23907081
#SPJ4
in a survey of 100 people, 60 like farming and 65 like civil service. find the number of people who likes farming as well as civil service. also find out how many people like only civil war
Answers
Let
A=set of people like farmingB=set of people like civil service A\(\cup\) B =Total peopleA\(\cap\)B=People like bothWe know
\(\boxed{\sf n(A\cup B)=n(A)+n(B)-n(A\cap B)}\)
\(\\ \sf\longmapsto n(A\cap B)=n(A)+n(B)-n(A\cup B)\)
\(\\ \sf\longmapsto n(A\cap B)=60+65-100\)
\(\\ \sf\longmapsto n(A\cap B)=125-100\)
\(\\ \sf\longmapsto n(A\cap B)=25\)
DRIVING Winston drove a total of 248 miles on Monday. He drove 70 fewer miles in the morning than he did in the afternoon. How many miles did he drive in the afternoon?
Answers
In the afternoon, Winston traveled a distance of 159 kilometers.
What is the distance?A mathematical number known as distance measures "how much ground an object has traveled" while moving. Distance is defined as the product of speed and time.
On Monday, Winston covered a distance of 248 miles. In the morning, he covered 70 fewer miles than in the afternoon.
Let "x" be the number of miles Winston drove in the afternoon.
In the morning, Winston drove x - 70 miles.
In total, Winston drove 248 miles on Monday.
So, x + (x - 70) = 248
2x - 70 = 248
2x = 318
x = 318/2
Apply the division operation, and we get
x = 159
Thus, Winston drove 159 miles in the afternoon.
Learn more about the distance here:
brainly.com/question/13269893
#SPJ1