Answers
Answer:
\(x=4\)
Step-by-step explanation:
start by squaring both sides:
\((\sqrt{-8+3x} )^2=(2)^2\)
squaring a square root cancels it out:
\(-8+3x = 4\)
solve for x by first adding 8 to both sides:
\(3x=12\)
then divide both sides by 3:
\(x=4\\\)
Related Questions
Write each fraction as a mixed number.
3 4/9
43/9
32/5
Answers
The value of the fractions in the mixed fraction form is 3(⁷/₉), 4(⁷/₉), and 6(²/₅) respectively.
What is a mixed fraction?A mixed fraction is a fraction that is created by fusing a fraction with a whole number. The fraction is defined as the division of the whole part into an equal number of parts.
The given fractions 34/9, 43/9, and 32/5 can be written in the form of the mixed fraction as below:-
To write the fractions in the form of the mixed fraction first divide the fraction by the complete number and put the remainder on the numerator.
34/9 = 3(⁷/₉)
43/9 = 4(⁷/₉)
32/5 = 6(²/₅)
Therefore, the value of the fractions in the mixed fraction form is 3(⁷/₉), 4(⁷/₉), and 6(²/₅) respectively.
To know more about a mixed fraction follow
https://brainly.com/question/1746829
#SPJ1
pls aswer!!!
and give simple workingout

Answers
The n-ary rule for linear sequences is 7n - 1. The given sequence is an arithmetic sequence.
What is Arithmetic Progression?
Any two consecutive integers in a sequence are in "arithmetic progression" (AP) if their difference is constant.
The formula is given by Tn = a + (n - 1) d. where,
a, first term = 6 n, number of terms
d, binomial tolerance = 13 - 6 = 7
So substitute the value into the equations. It will be as follows.
Tn = a + (n - 1)d
= 6 + (n - 1)7
= 6 + 7n - 7
= 7n - 1
So the n term of this sequence is 7n - 1.
To learn more about equations, visit:
https://brainly.com/question/10413253
#SPJ1
Select the correct answer.
Which of the following represents a function?
A. The first graph
B. The second graph
C. {(0,1), (3,2), (-8,3), (-7,2), (3,4)}
D.
x -5 -1 9 8 -1
y 1 7 23 17 1


Answers
Answer:
The answer is to the question A
Answer:
Its B 100%
i took the test and got it right
k bye :):):):):):):)
Step-by-step explanation:
Write the slope intercept form of the equation of the line through the given points.
through: (0, 2) and (-4, -1)
Answers
Answer:
You use the formula (y to the second power minus y to the first power minus the same formula with the two different points
Step-by-step explanation:
Find the length of the missing side. Assume that lines that appear to be tangent are tangent. Round your answer to the nearest tenth, if needed.

Answers
Solution:
Given:
The radius and tangent to a circle at the point of intersection are perpendicular to each other.
Hence, considering the right triangle;
Hence, the length of the missing side can be gotten using the Pythagorean theorem.
\(\begin{gathered} first\text{ leg}^2+other\text{ leg}^2=hypotenuse^2 \\ 8.4^2+x^2=10.5^2 \\ x^2=10.5^2-8.4^2 \\ x^2=39.69 \\ x=\sqrt{39.69} \\ x=6.3 \end{gathered}\)
Therefore, to the nearest tenth, the length of the missing side is 6.3


Please help with this question
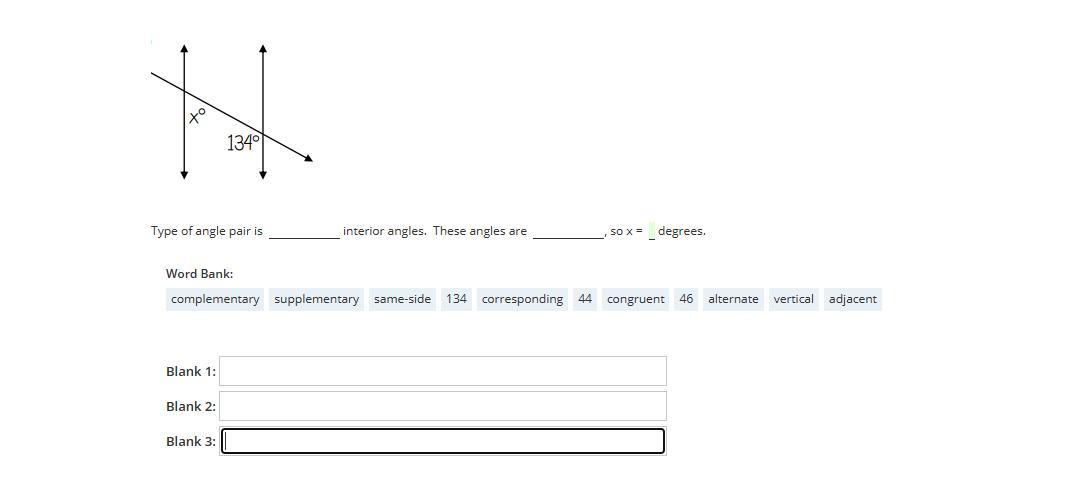
Answers
Blank 1: Corresponding because All angles that are either exterior angles, interior angles, alternate angles or corresponding angles are all congruent.
Blank 2:
Blank 3: x= 46 as 180-134 = 46
Identify ALL solutions for the inequality −3x−5>10
Answers
Answer:
The solution set for this inequality is any number less than -5 or x < -5 (not including -5)Step-by-step explanation:
An inequality has two solutions, we have to figure out if x is greater than a number or less. There are a few special rules when solving inequalities.
1. When we divide by a negative number, we must reverse the inequality sign.
2. When we check the solution of an inequality, we need to try two numbers to ensure that we have the sign in the correct direction.
Let's solve!
Step 1: Add 5 to both sides-3x - 5 > 10
-3x - 5 + 5 > 15
-3x > 15
Step 2: Divide by -3-3x/-3 > 15/-3
Remember: When we divide by negative numbers, we must reverse the sign as seen below, so greater than becomes less than.
x < -5
Step 3: CheckNow we will check two different numbers from our solution set to ensure that we have the correct answer.
-3(-6) - 5 > 10
18 - 5 > 10
13 > 10 ✔️
Remember: When we check inequalities, we need to check two solutions, so we will go with -8 for the second check, since it is also less than -5.
-3(-8) - 5 > 10
24 - 5 > 10
19 > 10 ✔️
Step 4: AnswerThe solution set for this inequality is any number less than -5 or x < -5 (not including -5)
PLEASE HELP URGENTLY! RIGHT ANSWERS ONLY!

Answers
Answer:
Hi! The answer is B!
I would suggest using a graphing calculator to compare all the lines. You can use this free one called Desmos, sorry i was not able to attach a link :)
3 5/11 s a decimal exspansion
Answers
By rational number algebra, the mixed number 3 5 / 11 is equivalent to the decimal expansion 3.\(\overline {45}\).
How to transform a mixed number into a decimal number
According to the statement, we find a mixed number, that is, a notation to represent rational numbers that combines both integers and fractions. The procedure to obtain the decimal form of a mixed number is:
Transform the mixed number into a single rational number by using the following formula:a b / c = (a · c) / c + b / c, where a, b, c are integers and a ≠ 0.Divide the single rational number.
Then, the decimal expansion of the mixed number 3 5 / 11 is:
3 5 / 11 = (3 · 11) / 11 + 5 / 11 = 33 / 11 + 5 / 11 = 38 / 11 = 3.\(\overline {45}\)
To learn more on mixed numbers: https://brainly.com/question/24137171
#SPJ1
Hesperia Community center is buying new seating for their building. They want to purchase a combination of stools and chairs. Stool cost $15 and chairs cost $25. The center cannot spend more than 1500. Which inequality represents all possible combinations of s stools and c chairs? A. 15s + 25c < 1500 B. 15c + 25s > 1500 C. 15c + 25s < 1500 D. 15s + 25c < 1500
Answers
Answer:
I just finished taking the test and the answer is 15s + 25c ≤ 1500

two cyclists, 42 miles apart, start riding toward each other at the same time. one cycles 2 times as fast as the other. if they meet 2 hours later, what is the speed (in mi/h) of the faster cyclist?
Answers
The speed of the faster cyclist is 14\ miles/hr.
What is speed?
It is the average distance coverd in unit time. It is also defined as the rate of change of distance with respect to time.
Since the speed of the first cyclist is double than the second cyclist hence, the first cyclist will cover the double distance than the second cyclist. Consider the first cyclist covers 2s distance and first cyclist covers s distance. The sum of these two distances should be 42 miles. Hence,
\(2s+s=42\\3s=42\\s=14\)
Now, distance coverd by the first cyclist is \(2s=2\times 14\\=28 \ $miles\).
Now, both the cyclists meet after 2 hr hence, time taken by the first cyclist is 2 hr.
\(Speed=\frac{Total\ distance}{Total\ time}\\=28\ miles/2 \ hr\\=14\ miles/hr\)
Hence, the speed of the faster cyclist is 14\ miles/hr.
Learn more about speed from the following link:
https://brainly.com/question/13943409
#SPJ4
what is a chart or graph that presents grouped data with rectangular bars with lengths proportional to the values that they represent?
Answers
A chart or graph that presents grouped data with rectangular bars with lengths proportional to the values that they represent is known as a bar graph.
A bar graph is a way to visually represent data using rectangular bars with lengths proportional to the values that they represent.
The bars can be either vertical or horizontal, depending on the orientation of the graph. The vertical bars are known as a column graph, while the horizontal bars are known as a bar chart.
The purpose of a bar graph is to provide a clear and concise representation of data that is easy to understand and interpret. Bar graphs are commonly used to compare different sets of data or to track changes in data over time.
They can be used to show how a particular variable changes over time or to compare the values of different variables in a single graph.
Bar graphs are easy to read and interpret, making them a popular choice for both simple and complex data sets.
They are widely used in business, science, and education, among other fields, to present information in a clear and concise manner.
To learn more about : graph
https://brainly.com/question/19040584
#SPJ8
What is the area of the figure below?

Answers
Answer:
3 x 3 = 9 + 3 x 3 = 9 which would be 18, then add 7 and 3 which would be 10 then multiply it by 5 which would be 50 then divided by 2 and you would get 25 add 25 two times which would be 50 once you do, you add the 18 which would be 68 in square.
Step-by-step explanation:
C C
A student believes that a certain number cube is unfair and is more likely to land with a six facing up. The student rolls
the number cube 45 times and the cube lands with a six facing up 12 times. Assuming the conditions for inference
have been met, what is the 99% confidence interval for the true proportion of times the number cube would land with a
six facing up?
0. 27 2. 58
0. 221-0. 27)
45
0. 7342. 33
0. 731-0. 73)
45
0. 27 2. 33
0. 271 -0. 20)
45
0. 73 +2. 58
0. 73(10. 73)
45
Mix
Save and Exit
Answers
we can say with 99% confidence that the true proportion of times the number cube would land with a six facing up is between 0.05 and 0.49.
Find out the confidence interval for the true proportion of time?To find the 99% confidence interval for the true proportion of times the number cube would land with a six facing up, we can use the formula:
CI = p ± zsqrt(p(1-p)/n)
where:
CI is the confidence interval
p is the sample proportion (number of times the cube landed with a six facing up divided by the total number of rolls)
z is the z-score corresponding to the desired confidence level (99% in this case)
n is the sample size (45 in this case)
First, let's calculate the sample proportion:
p = 12/45 = 0.27
Next, we need to find the z-score corresponding to a 99% confidence level. Using a standard normal distribution table or calculator, we find that the z-score is 2.58.
Now we can plug in the values and calculate the confidence interval:
CI = 0.27 ± 2.58sqrt(0.27(1-0.27)/45)
CI = 0.27 ± 0.22
CI = (0.05, 0.49)
The number cube would land with a six facing up between 0.05 and 0.49.
Learn more about Proportion
brainly.com/question/1496357
#SPJ11
Prove these triangles are similar using AA criterion. (LT # 3.1)
Show Your Work
(I need help ASAPP!!)

Answers
Find an equation for the line tangent to the graph of the given function at the indicated point. 8 3) f(x): () = at at (4,2) X 1 4) f(x)=x2-x at (4, 12)
Answers
(a) tangent line to the graph of f(x) = x^3 at the point (4,2).
(b) equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12).
(a) To find the equation of the tangent line to the graph of f(x) = x^3 at the point (4,2), we need to find the slope of the tangent line at that point. We can do this by taking the derivative of f(x) with respect to x and evaluating it at x = 4. The derivative of f(x) = x^3 is f'(x) = 3x^2. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Once we have the slope, we can use the point-slope form of a linear equation to write the equation of the tangent line.
(b) Similarly, to find the equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12), we differentiate f(x) to find the derivative f'(x). The derivative of f(x) = x^2 - x is f'(x) = 2x - 1. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Using the point-slope form, we can write the equation of the tangent line.
In both cases, the equations of the tangent lines will be in the form y = mx + b, where m is the slope and b is the y-intercept.
Learn more about line tangent: brainly.com/question/30162650
#SPJ11
abby is comparing monthly phone charges from two companies. phenix charges $30 plus $.5 per minute. Nuphone charges $40 plus $.10 per minute. in how many minutes will the total be the same
Answers
Answer:
In 25 minutes, the monthly phone charges of both companies will be the same.
Step-by-step explanation:
If we allow m to represent the number of minutes, we can create two equations for C, the total cost of phone charges from both companies:
Phoenix equation: C = 0.5m + 30
Nuphone equation: C - 0.10m + 40
Now, we can set the two equations equal to each other. Solving for m will show us how many minutes must Abby use for the total cost at both companies to be the same:
0.5m + 30 = 0.10m + 40
Step 1: Subtract 30 from both sides:
(0.5m + 30 = 0.10m + 40) - 30
0.5m = 0.10m + 10
Step 2: Subtract 0.10m from both sides:
(0.5m = 0.10m + 10) - 0.10m
0.4m = 10
Step 3: Divide both sides by 0.4 to solve for m (the number of minutes it takes for the total cost of both companies to be the same)
(0.4m = 10) / 0.4
m = 25
Thus, Abby would need to use 25 minutes for the total cost at both companies to be the same.
Optional Step 4: Check the validity of the answer by plugging in 25 for m in both equations and seeing if we get the same answer:
Checking m = 25 with Phoenix equation:
C = 0.5(25) + 30
C = 12.5 + 30
C = 42.5
Checking m = 25 with Nuphone equation:
C = 0.10(25) + 40
C = 2.5 + 40
C = 42.5
Thus, m = 25 is the correct answer.
Question 1
4 pts
Rewrite each equation so that the expression on one side could be graphed and the x-
intercepts of the
graph would show the solutions to the equation.
a. 3r? = 81
b. (x-1)(x+1)-9=5x
Cr? - Sx + 10 = 32
d. 6x(x-8)=29
Answers
The equations will be re-written such that the expression on one side can be graphed and the x-intercepts of the graph would indicate the solution.
What are the re-written equations?A) 3X² = 81
Rewritten, we have 3X² - 81 = 0
This is also = 3(X² - 27) = 0
B) (X - 1)(X + 1) - 9 = 5X
Open the brackets and we have X² - 1 - 9 - 5x = 0
Simplified, we have X² - 5X - 10 = 0
C) X² - 9x + 10 = 32
Collect like terms and we have:
X² - 9X - 22 = 0
D) 6x(x - 8) = 29
Expand the bracket and collect like terms such that the equation is equal to zero and we have
6X² - 48x - 29 = 0
Using Desmos Graphing, the following results can be obtained showing that x intercepts at:
(a) (-5.196, 0) & (5.196, 0)
(b) (-1.531, 0) & (6.531, 0)
(c) (-2, 0) & (11, 0)
(d) (-0.564, 0) & (8.564, 0)
Learn more about graphed equations at:
https://brainly.com/question/14323743
Sarah has been running a dog-walking business since 2010. She walks dogs twice a day, takes them to the park, and returns them to their homes. Each year, she has increased her fee by the same amount. The table shows what Sarah charged each customer for two given years of her business:
Year Annual Dog-walking Fee
2010 $350
2014 $750
A. What is the rate of change and initial value for Sarah's business? How do you know?
B. Write an equation in slope-intercept form to represent the fees that Sarah charges each year. (10 points)
Answers
Sarah's company started out with a $350 value and is currently changing at a rate of $100 annually.
The annual fee is expressed as an equation in slope-intercept form:
y = 100x + 350.
Define the term slope-intercept form?y = mx + b, where m is the line's slope and b is its y-intercept, is the formula for a straight line.
Given details:
Since 2010, Sarah has operated a dog-walking service.She has raised her rate the same amount each year.The table displays the prices that Sarah charged each client during the course of her business's first two years:
Year Annual Dog-walking Fee
2010 $350
2014 $750
A.
Sarah has so increased the cost by $400 over the past four years.
For Sarah's company, its rate of change called slope will be,
m = 750 - 350 / 4
m = 100
Therefore, Sarah is raising the cost by $100 yearly.
Due to the payment she received for the first year, the calculated values of a business is $350.
B. Define x as the period of time that has passed since she began her business in 2010.
Consequently, the annual fee equation can be expressed in slope-intercept form as,
y = mx + c
where y stands for the cost she must pay after x years.
Her company's baseline value is therefore $350, and its rate of change is $100 annually.
The annual fee is expressed as an equation in slope-intercept form.: y = 100x + 350.
To know more about the slope-intercept form, here
https://brainly.com/question/1884491
#SPJ1
identify the number and type of solutions for the equation 9x2 − 12x 4 = 0.
Answers
Answer:
9x^2-12x+4=0
Step-by-step explanation:
you can use factorization method or Quadratic method (Almighty formular).
The number of the solution of the equation is 2 and the solution is equal and real which is 2/3.
What is the solution to the equation?The allocation of weights to the important variables that produce the calculation's optimum is referred to as a direct consequence.
The quadratic equation is ax² + bx + c = 0. Then the discriminant is given as,
D = b² - 4ac
If D > 0, then the roots are real and distinct root.If D = 0, then the roots are real and equal roots.If D < 0, then the roots are imaginary roots.The equation is given below.
9x² - 12x + 4 = 0
The discriminant is given as,
D = (-12)² - 4 x 9 x 4
D = 144 - 144
D = 0
Then the roots of the equation is given as,
9x² - 12x + 4 = 0
(3x)² - 2 · 3x · 2 + (2)² = 0
(3x - 2)² = 0
x = 2/3
The number of the solution of the equation is 2 and the solution is equal and real which is 2/3.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ12
A thin wire is bent into the shape of a semicircle x2+y2=64,x>=0. If the linear density is a constant k, find the mass and center of mass of the wire.
mass = _____
center of mass (¯x,¯y)(x¯,y¯) = ( _____ )
Answers
The center of mass of the wire is (64/15, 0). To find the mass of the wire, we need to calculate its length first.
Since the wire is bent into the shape of a semicircle, its length is half the circumference of a circle with radius 8 units (since x>=0). Therefore, the length of the wire is πr = π(8) = 8π.
The linear density of the wire is given as k, which means that its mass per unit length is k. Thus, the mass of the wire is the product of its length and linear density: mass = k(8π) = 8kπ.
To find the center of mass, we need to locate the centroid of the semicircle. By symmetry, the centroid lies on the x-axis, and we only need to find its x-coordinate.
The x-coordinate of the centroid can be found using the formula:
x¯ = (1/M) ∫(x dM)
where M is the mass of the wire, and the integral is taken over the semicircle.
Using polar coordinates (x = rcosθ, y = rsinθ), we can rewrite the equation of the semicircle as y = (64-x^2)^0.5.
Then, we have:
dM = kds = k(sqrt(1+(dy/dx)^2))dx = k(1+(x^2/(64-x^2)))^(1/2) dx
Integrating from x=0 to x=8, we have:
x¯ = (1/M) ∫(x dM) = (1/8kπ) ∫(x (1+(x^2/(64-x^2)))^(1/2) dx) = 64/15
Therefore, the center of mass of the wire is (64/15, 0).
Learn more about length here:
https://brainly.com/question/32060888
#SPJ11
Hen interpreting f (7, 31) = 4.78, p > 0.05. How many subjects were tested in this simple one-way anova?
Answers
39 subjects were tested in this simple one-way ANOVA.
The df for F distribution is (treatment df, error df)
Using given information
Treatment df = 7
Error df = 31
Total df= 7+31 = 38
Again, total df = N-1, N= number of subjects tested
Then, N-1 = 38
=> N= 39
One-way ANOVA is typically used when there is a single independent variable or factor and the goal is to see whether variation or different levels of that factor have a measurable effect on the dependent variable.
The t-test is a method of determining whether two populations are statistically different from each other, and ANOVA determines whether three or more populations are statistically different from each other.
Learn more about one-way ANOVA here: brainly.com/question/24157862
#SPJ4
A boat can travel 32 miles on 4 gallons of gasoline. How much gasoline will it need to go 48 miles?
Answers
Answer:
6 gallons
Step-by-step explanation:
32/4=8
48/8=6
Answer: 6
Step-by-step explanation: If 4 gallons can take you 32 miles, divide 4 into 32 to get 8. That means 8 miles is 1 gallon. Now just do 48/8 to get 6.
If I1 ⊇ I2 ⊇ .... In ⊇... is a nested sequence of intervals and if In = [an; bn], show that a1 ≤ a2 ≤ ....... ≤ an ≤ ........ and b1 ≤ b2 ≤..... bn ≤ ......
Answers
The intervals are nested, each subsequent interval is contained within the previous one. Mathematically, this means I₁ ⊇ I₂ ⊇ ... In ⊇ ... . Therefore, we have:
1. I₁ ⊇ I₂ implies [a₁; b₁] ⊇ [a₂; b₂], which means a₁ ≤ a₂ and b₁ ≥ b₂.
2. I₂ ⊇ I₃ implies [a₂; b₂] ⊇ [a₃; b₃], which means a₂ ≤ a₃ and b₂ ≥ b₃.
To show that a1 ≤ a2 ≤ ... ≤ an ≤ ..., we need to use the fact that the sequence of intervals is nested, meaning that each interval is contained within the next one.
First, we know that I1 contains I2, so every point in I2 is also in I1. That means that a1 ≤ a2 and b1 ≥ b2.
Now consider I2 and I3. Again, every point in I3 is also in I2, so a2 ≤ a3 and b2 ≥ b3.
We can continue this process for all the intervals in the sequence, until we reach In. So we have:
a1 ≤ a2 ≤ ... ≤ an-1 ≤ an
and
b1 ≥ b2 ≥ ... ≥ bn-1 ≥ bn
This shows that the endpoints of the intervals are ordered in the same way.
Given that I₁ ⊇ I₂ ⊇ ... In ⊇ ... is a nested sequence of intervals and In = [an; bn], we can show that a₁ ≤ a₂ ≤ ... ≤ an ≤ ... and b₁ ≥ b₂ ≥ ... ≥ bn ≥ ... as follows:
Since the intervals are nested, each subsequent interval is contained within the previous one. Mathematically, this means I₁ ⊇ I₂ ⊇ ... In ⊇ ... . Therefore, we have:
1. I₁ ⊇ I₂ implies [a₁; b₁] ⊇ [a₂; b₂], which means a₁ ≤ a₂ and b₁ ≥ b₂.
2. I₂ ⊇ I₃ implies [a₂; b₂] ⊇ [a₃; b₃], which means a₂ ≤ a₃ and b₂ ≥ b₃.
Continuing this pattern for all intervals in the sequence, we can conclude that a₁ ≤ a₂ ≤ ... ≤ an ≤ ... and b₁ ≥ b₂ ≥ ... ≥ bn ≥ ... .
Visit here to learn more about sequence : https://brainly.com/question/30262438
#SPJ11
The graph of the function g(x) is a transformation of the parent function f(x)=x2.
Which equation describes the function g?
g(x)=x2+4
g(x)=x2−4
g(x)=(x+4)2
g(x)=(x−4)2

Answers
Answer:
g(x)=x2-4
Step-by-step explanation:
The numerical of the graph g(x) = x² - 4 shifted 4 units down.
What are some rules of function transformations?Suppose we have a function f(x).
f(x) ± d = Vertical upshift/downshift by d units (x, y ±d).
f(x ± c) = Horizontal left/right shift by c units (x - + c, y).
(a)f(x) = Vertical stretch for a > 0, vertical shrink a < 0. (x, ay).
f(bx) = Horizonatal compression b > 0, horizontal stretch for b < 0. (bx , y).
f(-x) = Reflection over y-axis, (-x, y).
-f(x) = Reflection over x-axis, (x, -y).
Given, The parent function is f(x) = x² which is a parabola that opens upwards and has a vertex at (0, 0).
Now, The transformed graph of f(x) which is g(x) = x² - 4 as the graph has shifted 4 units down along the y-axis.
learn more about the transformation of graphs here :
https://brainly.com/question/10059147
#SPJ2
The final exam scores in a statistics class were normally distributed with a mean of 70 and a standard deviation of five. What is the probability that a student scored less than 55% on the exam?
Answers
The probability that a student scored less than 55% on the exam is 0.134%.
What is a normal distribution?It's the probability curve of a continuous distribution that's most likely symmetric around the mean. On the Z curve, at Z=0, the chance is 50-50. A bell-shaped curve is another name for it.
We have:
Mean of the sample = 70
Standard deviation = 5
= P(X<55%)
Z = (55-70)/5
Z = -3
P(X < -3)
From the Z table:
P(x<-3) = 0.0013499
or
P(x<-3) = 0.134%
Thus, the probability that a student scored less than 55% on the exam is 0.134%.
Learn more about the normal distribution here:
brainly.com/question/12421652
#SPJ1
On a town map, each unit of the coordinate plane represents 1 mile. Three branches of a bank are located at A(−3, 1), B(3, 4), and C(3, −2). A bank employee drives from Branch A to Branch B and then drives halfway to Branch C before getting stuck in traffic. What is the minimum total distance the employee may have driven before getting stuck in traffic? Round to the nearest tenth of a mile if necessary.
The minimum total distance the employee may have driven before getting stuck in traffic is ____ miles.
Answers
Answer:
9.7 miles
Step-by-step explanation:
The shortest distance between 2 points is a straight line
The distance from point A to point B is
d = sqrt( ( x2-x1)^2 + ( y2-y1) ^2)
d = sqrt( ( 3 - -3)^2 + ( 4-1) ^2)
d = sqrt( ( 6)^2 + ( 3) ^2)
d = sqrt(36+9)
d = sqrt(45)
d =6.7 to the nearest tenth
The distance from point B to point C is
d = sqrt( ( x2-x1)^2 + ( y2-y1) ^2)
d = sqrt( ( 3 - 3)^2 + ( -2-4) ^2)
d = sqrt( ( 0)^2 + ( -6) ^2)
d = sqrt(36)
d = 6
But They only made it half way so 1/2 (6) =3
Add the distances together
6.7+3 = 9.7 is the minimum distance
Evaluate the following expression: \[ 1.723 \times 10^{2}+7.38 \times 10^{3} \] Type answer:
Answers
The sum of expression \(1.723 \times 10^{2}\) and \(7.38 \times 10^{3}\) is \(7.5523 \times 10^{3}\). The numbers in scientific notation are added by summing the coefficients while keeping the exponent unchanged.
In scientific notation, numbers are expressed as a coefficient multiplied by a power of 10. To add numbers in scientific notation, we need to ensure that the powers of 10 are the same.
In this case, both numbers are already in scientific notation with powers of 10. We can directly add the coefficients while keeping the exponent the same.
Adding \(1.723 \times 10^2\) and \(7.38 \times 10^3\) gives us a sum of \(7.5523 \times 10^3\). The coefficient represents the numerical value, and the power of 10 indicates the magnitude.
Thus, the expression \(1.723 \times 10^2 + 7.38 \times 10^3\) evaluates to \(7.5523 \times 10^3\), indicating a significant increase in magnitude compared to the individual numbers.
Learn more about Expression click here :brainly.com/question/24734894
#SPJ11
Find the maximum volume of a cylindrical soda can such that the sum of its height and its circumference is 150 cm.
Answers
20371.83 cm³ is the maximum volume of a cylinder.
What is volume?The space occupied within an object's borders in three dimensions is referred to as its volume.
It is sometimes referred to as the object's capacity.
So, consider a cylinder with a radius of r and a height of h.
The cylinder's volume is: V = πr²h
Because its height plus circumference equals 120 cm.
h + 2πr
h = 120 - 2πr
Changing the value of h in the cylinder's volume equation:
V = πr² (120-2πr)
V = 120πr² - 2π²r³
To get the biggest volume, compare the above expression to r and equate it to zero:
dV/dx = 240πr - 6π²r² = 0
6πr(πr-0) = 0
r = 0, r = 40/π
The cylinder's radius is: r = 40/π
Now: h = 120 - 2π(40/π) = 80cm
Changing the values of r and h in the cylinder's volume formula:
V = π(40/π)²*40 = 20371.83 cm³
Value of π = 3.14
Therefore, 20371.83 cm³ is the maximum volume of a cylinder.
Know more about volume here:
https://brainly.com/question/1972490
#SPJ4
what percent of 240 is 10.8? if necessary, round to four decimal places.
Answers
To find the percentage, we can use the formula: (part/whole) x 100%. In this case, the part is 10.8 and the whole is 240. So, substituting these values in the formula, we get (10.8/240) x 100% = 4.5%. Therefore, 10.8 is 4.5% of 240. To round to four decimal places, we can keep the first four digits after the decimal point, which gives us 4.5000%.
To find what percent of 240 is 10.8, follow these steps:
Step 1: Write the problem as a proportion using the given values.
x% = (10.8 / 240)
Step 2: Convert the percentage to a decimal by dividing x by 100.
x/100 = (10.8 / 240)
Step 3: Solve for x by cross-multiplying.
100 * 10.8 = 240 * x
Step 4: Divide both sides by 240 to isolate x.
x = (100 * 10.8) / 240
Step 5: Calculate the value of x.
x = 1080 / 240
Step 6: Simplify the fraction and, if necessary, round to four decimal places.
x = 4.5000
Therefore, 10.8 is approximately 4.5000% of 240.
Learn more about percentage at: brainly.com/question/29306119
#SPJ11
