Answers
Explanation
let's remember some properties of the exponents numbers
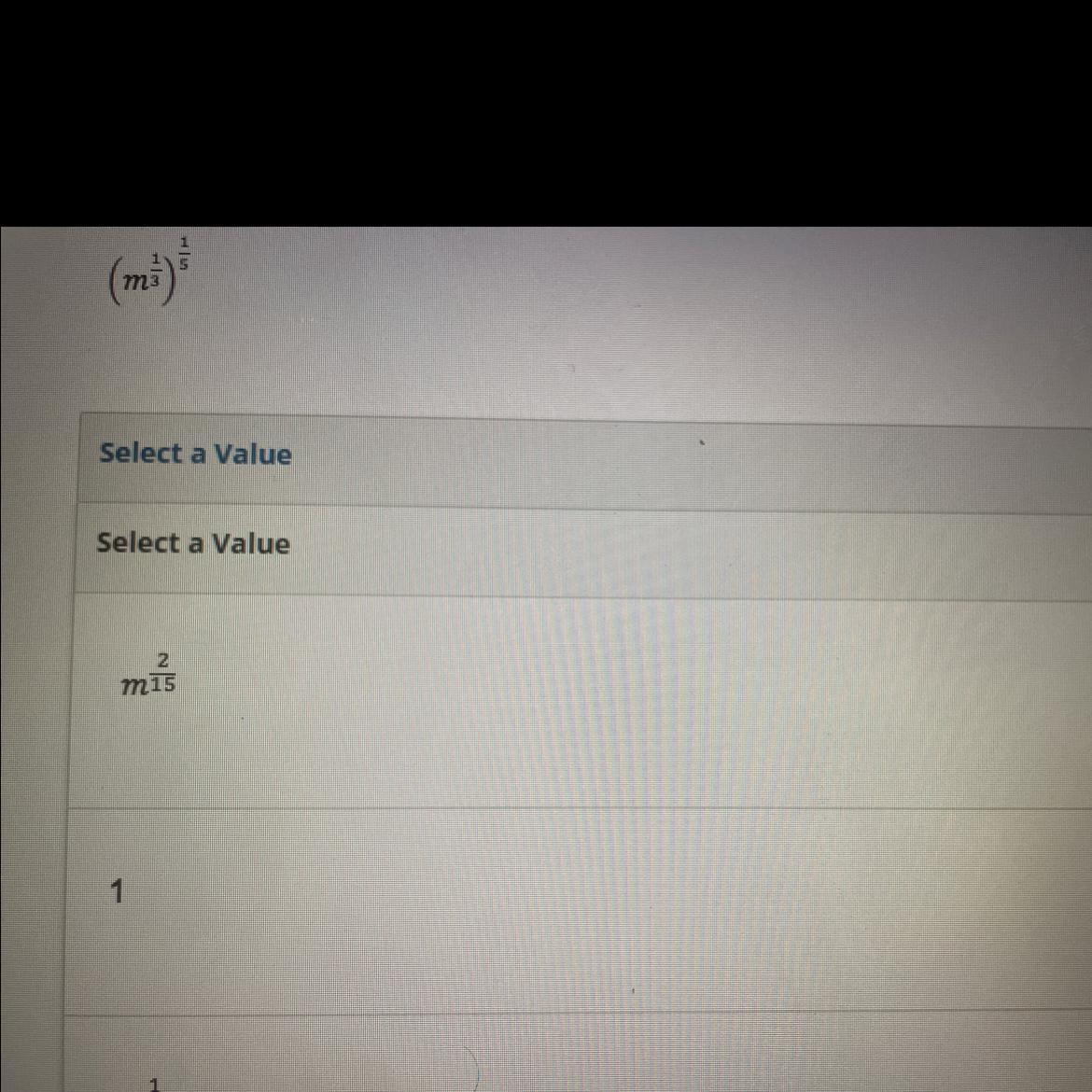
\(\begin{gathered} a^{\frac{1}{m}}=\sqrt[m]{a} \\ (a^m)^n=a^{m*n} \end{gathered}\)so
Step 1
\((m^{\frac{1}{3}})^{\frac{1}{5}}\)apply the properties to solve:
\(\begin{gathered} (m^{\frac{1}{3}})^{\frac{1}{5}}=m^{\frac{1}{3}*\frac{1}{5}} \\ (m^{\frac{1}{3}})^{\frac{1}{5}}=m^{\frac{1}{15}} \end{gathered}\)so, the answer is
\(m^{\frac{1}{15}}\)I hope this helps you
Related Questions
Please help!!!! I will give points to correct answer !!!

Answers
The equation that shows the Pythagorean identity is true for θ = 270° and is in the form sin²θ + cos²θ = 1 is option B. 0² + (-1)² = 1
The Pythagorean identity is a fundamental trigonometric identity that relates the sine and cosine functions. It states that for any angle θ, the sum of the squares of the sine and cosine of that angle is equal to 1: sin²θ + cos²θ = 1.
We are given θ = 270° and we need to select the equation that satisfies the Pythagorean identity in the given form.
Let's evaluate each option:
A. 0² + 1² = 1
In this case, sin²θ = 0² = 0 and cos²θ = 1² = 1. Adding them together, we get 0 + 1 = 1, which satisfies the Pythagorean identity.
B. 0² + (−1)² = 1
Here, sin²θ = 0² = 0 and cos²θ = (−1)² = 1. Adding them, we have 0 + 1 = 1, which satisfies the Pythagorean identity.
C. (−1)² + 0² - 1
In this equation, sin²θ = (−1)² = 1 and co
s²θ = 0² = 0. However, the equation does not satisfy the Pythagorean identity because 1 + 0 - 1 ≠ 1.
D. 1² + 0² = 1
For this option, sin²θ = 1² = 1 and cos²θ = 0² = 0. Adding them together, we get 1 + 0 = 1, which satisfies the Pythagorean identity.
Based on our evaluation, options A and B both satisfy the Pythagorean identity for θ = 270°. Therefore, either A or B can be selected as the correct equation.The correct answer is b.
Know more about Pythagorean identity here:
https://brainly.com/question/24287773
#SPJ8
The Question was Incomplete, Find the full content below :
Which equation shows that the Pythagorean identity is true for θ = 270°?
Select the equation that is in the form sin²θ+ cos²θ = 1.
A. 0² + 1² = 1
B. 0² + (−1)² = 1
C. (-1)² + 0² - 1
D. 1² + 0² = 1
Find the volume of the solid whose base is the semicircle y= squareroot( 16-x^2), where -4< x< 4 and whose cross section perpendicular axis are squares
Answers
The volume of the solid whose base is the semicircle y = √(16 - x²), where -4 < x < 4 and whose cross section perpendicular axis are squares is 256/3 unit³
To obtain the volume of a 3D shape, the cross-section area is discovered and then integrated across a predetermined limit. This technique is known as the cross-sectional method of volume fining. The area of the square base is determined in the given problem, and it is then integrated to determine the overall volume.
To find the volume we will first find the cross-sectional area and then integrate it with respect to x from -4 to 4.
Thus the volume is given as follows:
y = √(16 - x²)
V = ₋₄∫⁴ (√(16 - x²))² dx
V = ₋₄∫⁴ (16 - x²) dx
V = [16x - x³/3]₋₄⁴
V = (64 - 64/3 + 64 -64/3)
V = 256/3 unit³
To learn more about volume of the solid here;
brainly.com/question/29246646
#SPJ4
which ratio would not be long in the table of equivalent ratiosA. 2/7B. 4/16C. 8/28D. 10/35

Answers
Answer:
B. 4/16
Step-by-step explanation:
Two ratios are equivalent if the result of their divisions is 1.
Division of fraction: Multiplication of the numerator by the inverse of the denominator.
In this question:
We are given the ratio 6/21.
We are given four options, one of which is not equivalent to 6/21. We divide 6/21 by all of them, and find the result. The one which the result is not 1 is the one which is not equivalent.
A. 2/7
\(\frac{\frac{6}{21}}{\frac{2}{7}}=\frac{6}{21}\ast\frac{7}{2}=\frac{6\ast7}{21\ast2}=\frac{42}{42}=1\)B. 4/16
\(\frac{\frac{6}{21}}{\frac{4}{16}}=\frac{6}{21}\ast\frac{16}{4}=\frac{6\ast16}{21\ast4}=\frac{96}{84}\ne1\)These ratios are not equivalent, which means that B is the answer.
C. 8/28
D. 10/35
need help will give brainlist

Answers
Only set B: (-1,-3), (4,2), (6,4) appears to lie on the graph of a linear function, as the slopes between any two points remain constant.
To determine which set of points appears to lie on the graph of a linear function, we can check if the slope between any two points remains constant.
Let's calculate the slopes for each set of points:
A. (0,2), (3,1), (4,6)
The slope between (0,2) and (3,1):
m1 = (1 - 2) / (3 - 0) = -1/3
The slope between (3,1) and (4,6):
m2 = (6 - 1) / (4 - 3) = 5
We can see that the slopes are not equal, so this set of points does not lie on the graph of a linear function.
B. (-1,-3), (4,2), (6,4)
The slope between (-1,-3) and (4,2):
m1 = (2 - (-3)) / (4 - (-1)) = 5/5 = 1
The slope between (4,2) and (6,4):
m2 = (4 - 2) / (6 - 4) = 2/2 = 1
The slopes are equal, so this set of points appears to lie on the graph of a linear function.
C. (-3,-2), (0,0), (2,4)
The slope between (-3,-2) and (0,0):
m1 = (0 - (-2)) / (0 - (-3)) = 2/3
The slope between (0,0) and (2,4):
m2 = (4 - 0) / (2 - 0) = 4/2 = 2
The slopes are not equal, so this set of points does not lie on the graph of a linear function.
D. (5,-7), (0,-2), (2,2)
The slope between (5,-7) and (0,-2):
m1 = (-2 - (-7)) / (0 - 5) = 5/(-5) = -1
The slope between (0,-2) and (2,2):
m2 = (2 - (-2)) / (2 - 0) = 4/2 = 2
The slopes are not equal, so this set of points does not lie on the graph of a linear function.
Based on the calculations, only set B: (-1,-3), (4,2), (6,4) appears to lie on the graph of a linear function, as the slopes between any two points remain constant.
Learn more about slopes at:
https://brainly.com/question/3493733
#SPJ1
What is the equation of the parabola shown with its focus on this graph?

Answers
Answer:
C
Step-by-step explanation:
the directrix and focus are equidistant from the vertex
vertex = (0, 1 ) and focus = (0, - 2 ) then directrix is a horizontal line above the vertex with equation
y = 4
the focus and directrix are equidistant from any point (x, y ) on the curve.
using the distance formula
\(\sqrt{x-0)^2+(y-(-2))^2}\) = | y - 4 |
\(\sqrt{x^2+(y+2)^2}\) = | y - 4 | ( squaring both sides )
x² + (y + 2)² = (y - 4)²
x² + y² + 4y + 4 = y² - 8y + 16 ( subtract y² from both sides )
x² + 4y + 4 = - 8y + 16 ( add 8y to both sides )
x² + 12y + 4 = 16 ( subtract x² + 4 from both sides )
12y = - x² + 12 ( divide through by 12 )
y = - \(\frac{1}{12}\) x² + 1
Answer: Y = -\(\frac{1}{12}\)\(x^{2}\) + 1
Step-by-step explanation: Correct on Edmentum

which answer is it ? please help

Answers
It’ll come out to 5.3333 so it’ll be a greater-than or equal to sign.
N_<5
What is?
25% of 100 =
Pls hlp me
Answers
Answer:
25% of 100 =25/100×100=25
25×100/100
25
Therefore, 25 °/• of 100 is 25
ASAP!!! NEED AN ANSWER
In this budget scenario, use 15 per hour as the current wage for 40 hour work weeks. Hint: There are 52 weeks in a year, and 12 months in a year.
1. What is the gross yearly income?
2. What is the gross monthly income using this pay rate?
Answers
1)Gross Yearly Income = Hourly Wage × Hours per Week × Weeks in a Year
Gross Yearly Income = $15/hour × 40 hours/week × 52 weeks/year
Gross Yearly Income = $31,200
2)Gross Monthly Income = Gross Yearly Income / Months in a Year
Gross Monthly Income = $31,200 / 12 months
Gross Monthly Income ≈ $2,600
Write the equation of the line in fully simplified slope-intercept form.
-12-11-10-9-
12
11
10
9
R
5
4
2
654-3-2-1
-2
3
4
-5
-6
-8
6
-10
-11
-12
34567 8 9 10 11 12

Answers
The equation of the line in fully simplified slope-intercept form is y = x + 7.
We have,
From the graph,
The coordinates of the line are:
(0, 7), (-7, 0), and (-2, 5).
We can use any coordinates the line touches on the graph.
We will use,
(0, 7) and (-7, 0)
The equation can be written in the form y = mx + c
m = (0 - 7) / (-7 - 0)
m = -7/-7
m = 1 ______(1)
And,
(0, 7) = (x, y)
So,
y = mx + c ______(2)
7 = 1 x 0 + c
7 = c
c = 7 ______(3)
Now,
From (1), (2), and (3).
y = x + 7
Thus,
The equation of the line in fully simplified slope-intercept form is y = x + 7.
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ1
Let S be the universal set, where:
S= {1, 2, 3,..., 18, 19, 20}
Let sets A and B be subsets of S, where:

Answers
Answer:
Step-by-step explanation:
Therefore, the height of the tower is approximately 121.4 meters.
find the value of 11 (a + b) when a = 7 and b = 3. (a) 110
(b)77
(c) 11,000
(d) 44
Answers
Answer:
(a) 110
Step-by-step explanation:
We can plug in 7 for a and 3 for b. Then we can simplify
11(a + b)
11(3 + 7)
11(10)
110
Thus, the value of 11(a + b) when a = 7 and b = 3 is 110, or answer a
Which integers are opposites?
14 and –4
17 and –17
32 and –23
15 and –51
Answers
Answer:
A
Step-by-step explanation:
The opposite of an integer is the number on the opposite side of the number line with the same distance from zero. So, the integers that are opposites are 14 and -14, 17 and -17, 32 and -32, and 15 and -15. This is because these pairs have the same absolute value but different signs. For instance, the absolute value of 14 is 14, and the absolute value of -14 is also 14. Therefore, -14 is the opposite of 14. Similarly, -17 is the opposite of 17 and so on.
Answer:
a
Step-by-step explanation:
got it right on edge
The diameter of a circle is 18 centimeters. What is the circle's circumference?
Answers
Answer:
Circumference ≈ 56.55
Step-by-step explanation:
Given:
Diameter = 18 cmTo Find:
The circumference of the circleSolution:
Here we'll use the formula of finding the circumference,i.e :
\( \boxed{\rm \: C = πd}\)
Here, d = diameterThe value of π is not given, so let us take π = 3.14C = circumferenceSubstitute them onto the formula:
d = 18 cmπ = 3.14\(\rm C = \pi(18) \: cm\)
\(\rm C = 3.14 \times 18 \: cm\)
\( \boxed{\rm C \approx \: 56.55}\)
Hence, the circumference of the circle is 56.55(approx).
4x3 = -5x - 21 solve for x
Answers
To solve for x in the equation 4x3 = -5x - 21, we can follow these steps:
1. Move all the terms containing x to one side of the equation, and move the constant term to the other side. We can do this by adding 5x to both sides and then adding 21 to both sides:
4x3 + 5x = -21
2. Factor out x from the left-hand side of the equation:
x(4x2 + 5) = -21
3. Divide both sides by (4x2 + 5):
x = -21 / (4x2 + 5)
So the solution for x is x = -21 / (4x2 + 5). Note that this is a rational function, which means that the value of x depends on the value of the variable x. This equation has no real solutions because the denominator is always positive, and the numerator is negative.
Simplify the expression to a polynomial in standard form:
(2x+1)(x^2-6x+7)
Answers
The expression of a polynomial in standard form is mathematically given as
2 x^3-11 x^2+8 x+7
This is further explained below.
What is the expression of a polynomial in standard form?Generally, the equation for the polynomial is mathematically given as
(2x+1)(x^2-6x+7)
\((2 x+1)\left(x^2-6 x+7\right)\)
Expand\($(2 x+1)\left(x^2-6 x+7\right)$\) by multiplying each term in the first expression by each term in the second expression.
\(2 x \cdot x^2+2 x(-6 x)+2 x \cdot 7+1 x^2+1(-6 x)+1*7\)
Simplify terms
Simplify each term.
\($2 x^3-12 x^2+14 x+x^2-6 x+7$\)
Simplify by adding terms.
2 x^3-11 x^2+8 x+7
Read more about polynomials
https://brainly.com/question/11536910
#SPJ1
1. Which set of ordered pairs DOES NOT represent a function?
a. (0, 1), (2,3), (3,4), (5,6)
b. (1, 1), (2, 2), (3,3), (4,4)
c. (1,4), (1, 5), (1,6), (1,8)
d. (0,7), (2, 4), (4,7), (5,7)
Answers
Answer:
C.
Step-by-step explanation:
because x value cannot be repeated in an ordered pair
compare the following rational number
\( \frac{4}{5} and \frac{7}{5} \)
Answers
Answer:
7/5 is greater than 4/5
Answer:
\(\frac{4}{5}\) < \(\frac{7}{5}\)
fifteen less than the product of twenty-three and 2.8
Answers
(23 * 2.8) - 15
23 * 2.8 = 64.4
64.4 - 15 = 49.4
In 1986 a family member invested$ 100 each month into savings account with an interest rate of 0.25% that didn't change. In 2016 you decided you needed to use that saved up money for a big purchase so you cash the savings account out
Answers
Complete question is;
In 1986, a family member invested $100 each month into a savings account with an interest rate of 0.25% (that didn't change). In 2016, you decided you needed to use that saved up money for a big purchase, so you cash the savings account out.
How much money should be in the account using the FV formula?
Answer:
FV = $107.78
Step-by-step explanation:
We are given;
Present value; PV = 100
Interest rate; r = 0.25% = 0.0025
We are told the PV was in 1986 and In 2016 you decided you needed to use that saved up money .
This is a period of 30 years.
Thus, the number of compounding periods is n = 30
Formula for FV is;
FV = PV(1 + r)ⁿ
FV = 100(1 + 0.0025)^(30)
FV = $107.78
Write the numbers below in order
from least to greatest.
1.4 10.4 1.45 1.54 10.54
Answers
Answer:
Step-by-step explanation: 1.4 - 1.45 - 1.54 - 10.4 - 10.54
Least to greatest
Simplify
8!/(8-2)
A. 720
b. 0.018
C. 8
d. 56
e. 40320
f. 1.333
Answers
Answer:
D) 56
Step-by-step explanation:
\(\displaystyle \frac{8!}{(8-2)!}=\frac{8!}{6!}=\frac{8*7*6*5*4*3*2*1}{6*5*4*3*2*1}=8*7=56\)
A caterer prepares twice as many pizzas as she usually prepares for a large party. The caterer usually prepares 5 pizzas. The caterer also estimates that each party guest will eat
1
2
of a pizza.
Drag and drop each expression into the correct boxes to complete the explanation.
The expression that represents how many guests the pizzas can serve is .
How many party guests will the pizzas serve? Drag and drop the number of guests into the box.
The pizzas can serve guests.
Answers
Find x
14.2
18.5
find correct answer

Answers
From the circle the value of angle x is 90 degrees
We have to find the value of x
The radius of the circle is 18.5
As we observe the figure the angle x is opposite to the 90 degrees
The angle x and angle 90 degrees are vertical angles
We know that the vertical angles are equal or same
∠x = 90 degrees
Hence, the value of angle x is 90 degrees from the circle
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ1
I need to create a explicit formula

Answers
Answer:
2
Step-by-step explanation:
Mark and Don are planning to sell each of their marble collections at a garage sale. If Don has 1 more than 4 times the number of marbles Mark has, how many does each boy have to sell if the total number of marbles is 111?
Answers
On solving the provided question, we can say that in the equation,Often, there is only one variable, which also serves as the symbol. An illustration would be , \(D = 4(82-D)+2\)
What is equation?The equal sign (=), which denotes equality, is used to unite two statements in a mathematical equation. In algebra, an equation is a mathematical statement that proves the equality of two mathematical expressions.
For instance, the equal sign separates the variables 3x + 5 and 14 in the equation 3x + 5 = 14.The two sentences on either side of a letter are connected by a mathematical formula.
Each equation has a formula. Not every equation has a formula. Equations are created with the intention of being solved for a variable. If an equation meets the requirements for a function, it is a function. But not every equation is a function.
M+D = 82 marbles
\(M= 82- D\)
\(D= 4M+2\)
\(D= 4(82-D) +2\)
\(D= 328 - 4D+2\)
\(5D = 330\)
\(D= 66\)
Therefore, Don has 66 and Mark has 82-66 = 16
Learn more about equation here:
https://brainly.com/question/29657992
#SPJ4
Which of the following is the equation of the function f(x) graphed above? A. ƒ(x) = x(x − 2)²(x − 1)(x + 1) B. f(x) = (x - 2) (x − 1)(x + 1) c. f(x)= x(x - 2)²(x − 1)(x + 1) + 1)² D. f(x) = (x - 2)²(x - 1)(x - 1)^ E

Answers
The equation that Passes through the points (-4,2) and (5,-3)
Answers
Answer:
m= -5/9
Step-by-step explanation:
m= y2-y1/ x2-x1
m= -3-2/ 5-(-4)
m= -3-2/ 5+4
m= -5/9
y= mx + b
(-4,2)
2= -5/9(-4) + b
2= 2.2+ b
-2.2 +2= b
-0.2= b
Graph a line with a slope of 3/4 that contains the point (2,-3)
Answers
Answer:
\(y=\frac{3}{4} x-\frac{9}{2}\)
Step-by-step explanation:
Y=mx+c
Y=-3, X=2, m=3/4
(2)(3/4)=6/4=3/2
-3-3/2=-9/2
SO,
c=-9/2
Find the percent of markup for a shirt that a store buys for $3.25 and sells for $7.50.
Answers
A certain type of tree has seedlings randomly dispersed in a large area, with the mean density of seedlings being approximately five per square metre. If a forester randomly locates ten 1-square-metre sampling regions in the area, find the probability that none of the regions will contain seedlings.
Answers
Answer:
Step-by-step explanation:
The probability that the forester does not get the seedlings is 1/2 if the mean density of seedlings is 5 per square metre.
What is density?Density means the area within which a substance is collected or taken.
How to calculate the probability?We have been given the mean density =5 square metre.
And we have to calculate the probability that the forester will not get any seedlings.
So the probability that he will get the seedlings will be=5/10
which is 1/2
So the probability that he will not get the seedlings will be 1-1/2
that is 1/2.
Hence the probability that he will not get seedlings will be 1/2.
Learn more about probability at https://brainly.com/question/24756209
#SPJ2