Answers
Third angle of the required Triangle would be 80 Degrees and other two angles will be 50 Degrees.
What is Triangles ?Triangular polygons in geometry are those with three sides and have three vertices. There are three straight sides to this two-dimensional shape. Three-sided polygons also include triangles. A triangle's three angles add up to 180 degrees.
As two given angles are Base Angles
So, they are equal
(3x + 2) = (5x - 30)
2x = 32
x = 16
Putting x=16 in both the angles,
We get the required angle as 50 degrees.
Hence, sum of the angles of the triangle is 180 degrees.
So, 180 = 50 + 50 + x
We get the required angle as 80 degrees.
To learn more about Triangles, Visit:
https://brainly.com/question/2773823
#SPJ1
Related Questions
A zip wire runs between two posts, 25m apart. The zip wire is at an angle of 10 degrees to the horizontal. Calculate the length of the zip wire.
∘
to the horizontal. Calculate the length of the zip wire
Answers
The length of the zip wire, with a 10-degree angle to the horizontal and a distance of 25 meters between the posts, is approximately 25.35 meters.
To calculate the length of the zip wire, we can use trigonometry. Let's consider the triangle formed by the zip wire, where the horizontal distance between the two posts is 25 meters and the angle between the zip wire and the horizontal is 10 degrees.
Using trigonometric functions, we can determine the length of the zip wire. In this case, we'll use the sine function because we have the opposite side (the vertical distance) and we want to find the hypotenuse (the length of the zip wire).
The formula for sine is:
sin(angle) = opposite / hypotenuse
Rearranging the formula, we have:
hypotenuse = opposite / sin(angle)
In this case, the opposite side is the vertical distance, which is h.
So, the formula becomes:
hypotenuse = h / sin(angle)
To find h, we can use the formula for the length of the zip wire:
h = 25 * tan(angle)
Substituting this into the previous formula, we get:
hypotenuse = (25 * tan(angle)) / sin(angle)
Calculating the value, we have:
hypotenuse = (25 * tan(10°)) / sin(10°)
Using a calculator, we find:
tan(10°) ≈ 0.1763
sin(10°) ≈ 0.1736
Substituting these values, we can calculate the length of the zip wire:
hypotenuse ≈ (25 * 0.1763) / 0.1736 ≈ 25.35 meters
Therefore, the length of the zip wire is approximately 25.35 meters.
For more question on length visit:
https://brainly.com/question/28322552
#SPJ8
I need help this is almost due and i'm stuck please help I don't want to fail .

Answers
318 in^2
Explanation:
SA = 2(wl + hl + hw)
= 2(3(3) + 25(3) + (25)3)
= 2 (9 + 75 + 75)
= 2(159)
= 318 in^2
In a survey of 259 professional athletes, it was found that 110 of them owned a convertible, 91 of
them owned a giant screen TV, and 120 owned a sporting goods store. 15 owned a convertible and a
store, 43 owned a TV and a store, and 44 owned a covertible and a TV. 9 owned all three items.
1. How many athletes did not own any of the three items?
2. How many owned a covertible and a TV, but not a store?
3. How many athletes owned a convertible or a TV?
4. How many athletes owned exactly one type of item in the survey?
5. How many athletes owned at least one type of item in the survey?
6. How many owned a TV or a store, but not a convertible?
Answers
1. Number of athletes did not own any of the three items = 259 - 228
= 31.
2. Number of athletes own a convertible and a TV but not a store = 44 - 9
= 35.
3. Number of athletes own a convertible or a TV = 110 + 91 - 44
= 157.
4. Number of athletes owned exactly one type of item = 60 + 13 + 71 = 144.
5. Number of athletes owned at least one type of item = 259 - 31
= 228
6. Number of athletes own a TV or a store, but not a convertible = 13 + 34 +71
= 118.
The number of athletes did not own any of the three items need to subtract the number of athletes who own at least one item from the total number of athletes surveyed.
Total number of athletes surveyed = 259
Number of athletes own at least one item = 110 + 91 + 120 - 15 - 43 - 44 + 9 = 228
Number of athletes who did not own any of the three items = 259 - 228 = 31.
The number of athletes who owned a convertible and a TV but not a store need to subtract the number of athletes who own all three items from the number of athletes who own a convertible and a TV.
Number of athletes who own a convertible and a TV = 44
Number of athletes who own all three items = 9
Number of athletes who own a convertible and a TV but not a store = 44 - 9 = 35
The number of athletes who owned a convertible, or a TV need to add the number of athletes who own a convertible to the number of athletes who own a TV and then subtract the number of athletes own both a convertible and a TV.
Number of athletes who own a convertible or a TV = 110 + 91 - 44
= 157.
The number of athletes owned exactly one type of item need to add up the number of athletes who own a convertible only the number of athletes own a TV only and the number of athletes who own a store only.
Number of athletes own a convertible only = 110 - 15 - 9 = 86
Number of athletes own a TV only = 91 - 44 - 9 = 38
Number of athletes own a store only = 120 - 15 - 43 - 9 = 53
Number of athletes owned exactly one type of item = 60 + 13 + 71 = 144.
The number of athletes who owned at least one type of item can use the result from part (1).
Number of athletes who owned at least one type of item = 259 - 31
= 228
The number of athletes who owned a TV or a store but not a convertible need to subtract the number of athletes who own all three items, and the number of athletes own a convertible and a TV from the number of athletes own a TV or a store.
Number of athletes own a TV or a store = 91 + 120 - 43 - 9 = 159
Number of athletes own a TV or a store not a convertible = 13 + 34 +71
= 118.
For similar questions on athletes
https://brainly.com/question/25631156
#SPJ11
What decimal is being represented by the decimal grid?
a. 232
b. 23.2
c. 2.23
d. 2.32

Answers
Answer:
232
Step-by-step explanation:
232, because each has 100 squares so if you add the 2 filled squares you will get 200. Then if you count the last one only 32 is filled, when u add it it gives you 232
\(9 + 3 (10 ÷ 2) - 5^2\)
Answers
\(9+3(10 \div 2)-5^2\\\\=9+3(5)-25\\\\=-16+15\\\\=-1\)
3x-1/5=x+1/3
what is x
Answers
Answer:
Exact form:4/15
decimal form: 0.26(6 is repeating)
Step-by-step explanation:
Isolate the variable by dividing each side by factors that don't contain the variable.
Find non-invertible matrices A,B such that A+B is invertible. Choose A,B so that (1) neither is a diagonal matrix and (2) A,B are not scalar multiples of each other.A = [_____ _____][_____ _____]B = [_____ _____][_____ _____]
Answers
Matrices A and B are non-invertible matrices that can be added together to form an invertible matrix. To find these matrices, we can use the following steps:
Step 1: Choose a matrix A that is not a diagonal matrix and is not invertible. One example of such a matrix is
\(A = \left[\begin{array}{ccc}1&1\\0&0\end{array}\right]\)
Step 2: Choose a matrix B that is not a diagonal matrix, is not invertible, and is not a scalar multiple of matrix A. One example of such a matrix is
\(B = \left[\begin{array}{ccc}0&0\\1&1\end{array}\right]\)
Step 3: Add the matrices A and B together to form the matrix A+B. This matrix will be invertible, as shown below:
\(A+B = \left[\begin{array}{ccc}1&1\\0&0\end{array}\right]+\left[\begin{array}{ccc}0&0\\1&1\end{array}\right]=\left[\begin{array}{ccc}1&1\\1&1\end{array}\right]\)
Step 4: Verify that the matrix A+B is invertible by finding its determinant. The determinant of a 2x2 matrix is given by:
det(A+B) = (1)(1) - (1)(1) = 0
Since the determinant of the matrix A+B is not equal to zero, the matrix is invertible.
Therefore, the matrices \(A = \left[\begin{array}{ccc}1&1\\0&0\end{array}\right]\) and \(B = \left[\begin{array}{ccc}0&0\\1&1\end{array}\right]\) are non-invertible matrices that can be added together to form an invertible matrix \(A+B =\left[\begin{array}{ccc}1&1\\1&1\end{array}\right]\).
https://brainly.in/question/8463680
#SPJ1
Angle ABD is 90°
What is the measure of ZABC?
O A 360
O B. 54°
OC. 90°
OD. 126°
O E. 144º

Answers
you would do 90-36 to get the measure of angle ABC.
Need help pls ASAP no jokes need this badly

Answers
Answer:
x=64°
................
=============================================================
Explanation:
Combining all of the angles shown in the diagram leads to 360 degrees. This is because there are 360 degrees in a full rotation.
Let's add up the angles shown and set the sum equal to 360. Keep in mind that the square angle marker represents 90 degrees (aka a right angle).
180+26+x+90 = 180
x+296 = 360
x = 360-296
x = 64
please help me with my online classwork!

Answers
Answer:
840 cm²---------------------------
There are two triangular faces with base of 16 cm and height of 15 cm and three rectangular faces.
Find the sum of areas of all five faces:
S = 2*(1/2)*16*15 + (17*2 + 16)*12 = 240 + 600 = 840Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
make x the subject of the formula y= 2x +5
Answers
Answer:
x= (y-5)/2
Step-by-step explanation:
Isolate the x variable.
y= 2x +5
Subtract 5 from both sides.
y-5=2x
Divide both sides by 2.
(y-5)/2= x
Wildlife sanctuary has 38 species of birds.
They have 15 of each kind. A national
zoo in the same city has 42 species of
birds with 12 of each kind. Do they have
the same number of birds?
Answers
Firstly, solve 38C15.
Then solve 42C12.
Compare your answers.
The goal here is to see if 38C15 = 42C12.
Here is the formula:
nCr = n!/(r!(n - r)!
Go for it.
Simplify to a single trig function or constant with no fractions.

Answers
We can simplify cosec(t)tant(t) to sec(t). A trigonometric function is a mathematical function that relates the angles of a triangle to the ratios of its sides.
The most common trigonometric functions are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc).
To simplify the expression cosec(t)tant(t), we need to use the trigonometric identity:
cosec(t) = 1/sin(t)
tant(t) = sin(t)/cos(t)
Substituting these expressions into the original expression, we get:
cosec(t)tant(t) = (1/sin(t))(sin(t)/cos(t))
The sin(t) term in the numerator and denominator cancel out, leaving:
cosec(t)tant(t) = 1/cos(t)
Recalling the definition of secant, sec(t) = 1/cos(t), we can express the simplified expression as:
cosec(t)tant(t) = 1/sec(t)
Therefore, we can simplify cosec(t)tant(t) to sec(t).
Learn more about trigonometric identity :
https://brainly.com/question/3785172
#SPJ1
Which of the following sets of ordered pairs represents a function? PLEASE HELP
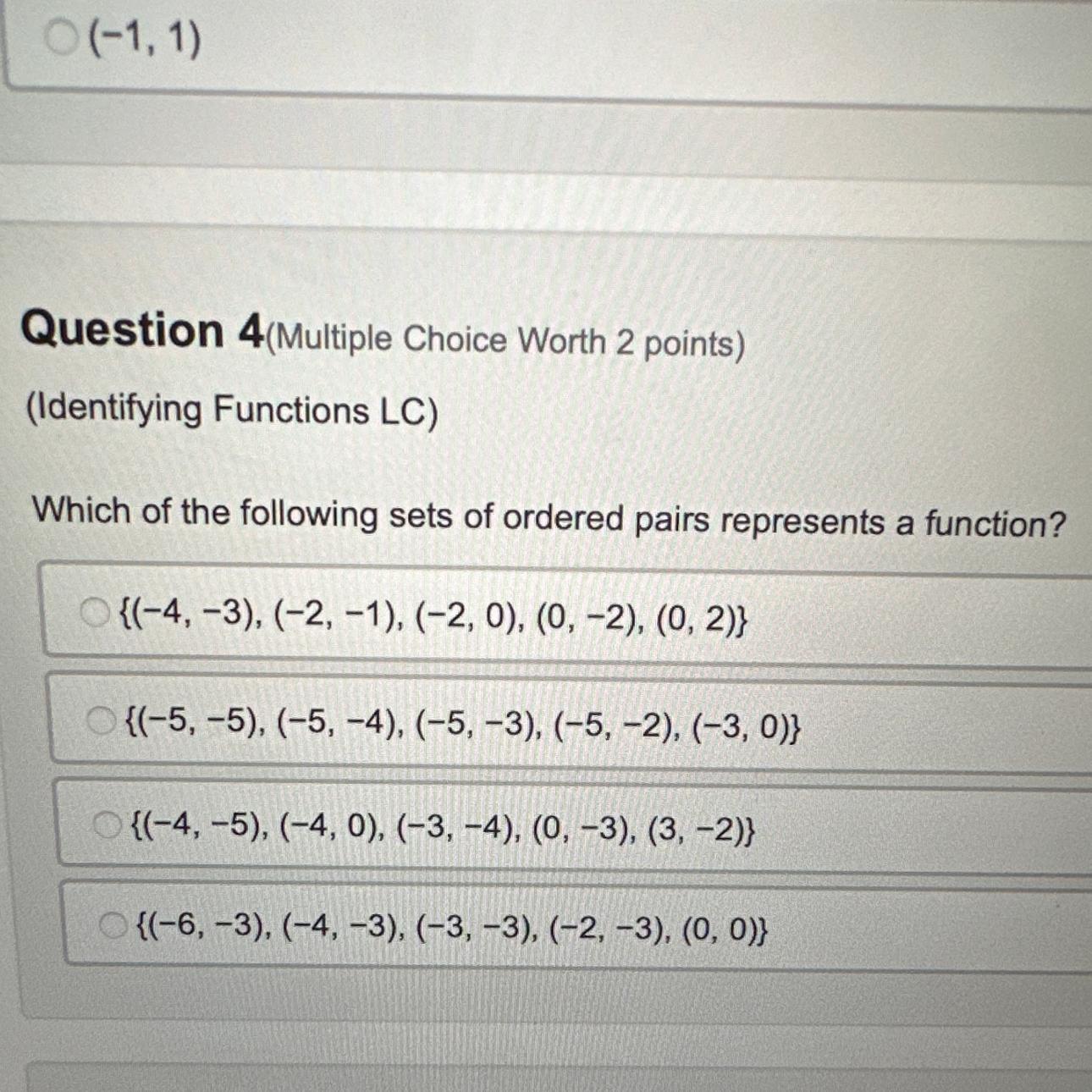
Answers
The set of ordered pairs that represents a function is (D) {(-6, -3), (-4, -3), (-3, -3), (-2, -3), (0, 0)}.
A set of ordered pairs represents a function if each unique input (x-value) is associated with only one output (y-value).
{(-4, -3), (-2, -1), (-2, 0), (0, -2), (0, 2)}
In this set, both (-2, -1) and (-2, 0) have the same x-value but different y-values. Therefore, this set does not represent a function.
{(-5, -5), (-5, -4), (-5, -3), (-5, -2), (-3,0)}
In this set, all the ordered pairs have the same x-value (-5). Since (-5, -5), (-5, -4), (-5, -3), and (-5, -2) have the same x-value but different y-values, this set does not represent a function.
{(-4, -5), (-4, 0), (-3, -4), (0, -3), (3, -2)}
In this set, (-4, -5) and (-4, 0) have the same x-value but different y-values. Therefore, this set does not represent a function.
{(-6, -3), (-4, -3), (-3, -3), (-2, -3), (0, 0)}
In this set, each unique x-value is associated with a single y-value. There are no repeated x-values. Therefore, this set represents a function.
To learn more on Sets click:
https://brainly.com/question/30705181
#SPJ1
here are (mutually exclusive) outcomes of a quarterback throwing a pass with their associated probabilities: complete pass (1/2), incomplete pass (1/4), interception (1/8), or fumble (1/8). p(interception or fumble)
Answers
The probability of an interception or fumble is 1/4.
The probability of an interception or fumble is 1/4. This is because the chances of an interception and fumble are mutually exclusive, meaning that they cannot both occur at the same time. Therefore, the probability of an interception or fumble is the sum of the probabilities for an interception (1/8) and a fumble (1/8), which is 1/4.
Probability of interception = 1/8
Probability of Fumble = 1/8
Probability of interception or fumble = 1/8 + 1/8 = 1/4
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
As a waiter, DaShawn earns $60 per week plus an average of $5 tip per table. This week, DaShawn wants his pay to be at least 250. Write an inequality to find the number of
tables DaShawn needs to serve to meet his goal, write, solve, and interpret an inequality for your final answer.
A. He should wait on no more than 30 tables to earn at least $250.
O
B. He should wait on at least 62 tables or fewer to cam at least $250.
O C. He should wait on at least 38 or more tables
earn at least $250
D. He should wait on less than 38 tables to earn less than $250.
Answers
Answer:
c
Step-by-step explanation:
Where is the central tendency located in a skewed left distribution?
to the left of the tallest bar
to the right of the smallest bar
to the left of the smallest bar
in the center of the graph
to the right of the tallest bar
Answers
The Central tendency is typically located to the right of the tallest bar.
In a skewed left distribution, the central tendency is typically located to the right of the tallest bar. Skewed left distributions, also known as negatively skewed distributions, are characterized by a tail that extends towards the left side of the distribution.
The central tendency refers to the measure that represents the center or average of a distribution. It provides information about the typical or central value around which the data points tend to cluster. Common measures of central tendency include the mean, median, and mode.
In a skewed left distribution, the mean is usually influenced by the long tail on the left side of the distribution. This tail pulls the mean towards lower values, resulting in a lower mean compared to the median. Therefore, the mean will typically be located to the left of the tallest bar in a skewed left distribution.
On the other hand, the median is less affected by the skewness of the distribution and is relatively robust to extreme values. It represents the value that separates the lower 50% of the data from the upper 50%. In a skewed left distribution, the median will be located closer to the tallest bar or even slightly to the right of it.
The mode, which represents the most frequently occurring value in a distribution, may or may not be influenced by the skewness depending on the shape of the distribution. It can be located anywhere along the distribution, and its position is not necessarily tied to the location of the tallest bar.
To summarize, in a skewed left distribution, the central tendency is typically located to the right of the tallest bar. The median is usually closer to the tallest bar or slightly to the right, while the mean is influenced by the skewness and tends to be located to the left of the tallest bar.
To know more about Central tendency.
https://brainly.com/question/1288901
#SPJ8
Lines that meet or cross each other to form square corners are called ______.
a.
parallel
b.
rays
c.
perpendicular
d.
intersecting
Answers
The lines that intersect to form square corners that are right angles are called: C. perpendicular lines.
What are Perpendicular Lines?Perpendicular lines are lines that intersect each other at a point and forms for square corners that are right angles at that point of intersection.
An example of perpendicular lines is shown in the image attached below.
Thus, the lines that meet to form right angles are called: C. perpendicular.
Learn more about perpendicular lines on:
https://brainly.com/question/1202004
#SPJ1

ACB = DCE
A=63
C=52
E=5x
what is X = ?

Answers
Answer: x=13
Step-by-step explanation:
given a segment ab, construct the point p on the segment that divides it into two segments such that the shorter is to the longer as the longer is to the whole
Answers
A segment ab, construct the point p on the segment that divides it into two segments such that the shorter is to the longer as the longer is to the whole .
Given :
given a segment ab, construct the point p on the segment that divides it into two segments such that the shorter is to the longer as the longer is to the whole .
You are asked to construct P such that :
PB / AP = AP / AB
This ratio is the reciprocal of the Golden Ratio.
( AP )^2 = PB * AB
( AP )^2 = PB * ( AP + BP )
( AP )^2 = PB ( AP ) + ( BP )^2
Divide by PB^2 on both sides
ф^2 = ф + 1
Learn more about the segment here:
https://brainly.com/question/12728072
#SPJ4
A spinner is divided into three sections: red, blue, and green. The red section is 2/5 of the area of the spinner. The blue section is 1/2 of the area of the spinner. Give the probability for each outcome. Express your answers as fractions.
Answers
Probability of red = \(\frac{4}{10}\) , blue = \(\frac{5}{10}\) , green = \(\frac{1}{10}\).
Meaning of probability :
Probability is calculation of how likely some event will happen. Whenever we are not sure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are going to happen.
The analysis of events governed by probability is called statistics.
According to the given information :
Red section = \(\frac{2}{5}\)
multiply numerator and denominator by \(2\) we get
Red section = \(\frac{4}{10}\)
Blue section = \(\frac{1}{2}\)
multiply numerator and denominator by \(5\) we get
Blue section = \(\frac{5}{10}\)
Green section = \(1\)- Red section - Blue section
Green section =\(1-\frac{4}{10} -\frac{5}{10}\)
Green section = \(\frac{1}{10}\)
Therefore Probability of red = \(\frac{4}{10}\) , blue = \(\frac{5}{10}\) , green = \(\frac{1}{10}\).
Learn more about Probability
https://brainly.com/question/11234923
#SPJ1
How to translate a equation to sentence 1/2(f+y)=f-5b
Answers
The translation of the statement is: Half the sum of the age of Francis and Yancy equals Francis' age less 5 multiplied by Bella's age
How to translate the equation into a sentence?The equation is given as:
1/2(f + y) = f - 5b
Before translating the equation, we make use of the following representations:
f represents Francis's agey represents Yancy's ageb represents Bella's ageUsing the above representations, we can translate the statement as:
Half the sum of the age of Francis and Yancy equals Francis' age less 5 multiplied by Bella's age
Read more about algebraic expressions at:
https://brainly.com/question/4344214
#SPJ1
Evaluate (-5z)^3 . Write your answer using only positive exponents. Evaluate any numerical powers.
Answers
Answer:
-125z³
Step-by-step explanation:
-5 times - 5 = 25 canceling negative
125 times -5 = -125
zXzXz = z to power of 3 =z³
38. Which of the following describes a median of a triangle? (1 point)
a segment drawn from a vertex to the midpoint of the opposite side
a segment drawn from the vertex perpendicular to the line containing the opposite side
a segment drawn through the midpoint of a side and at a right angle to the side.
segment drawn from the center of an angle to the side opposite.
Answers
A statement that describes the median of a triangle include the following: A. a segment drawn from a vertex to the midpoint of the opposite side.
What is a triangle?In Mathematics and Geometry, a triangle is a two-dimensional geometric shape that comprises three sides, three vertices and three angles only.
In Mathematics and Geometry, the median of a triangle can be defined as a line segment with end points that is typically drawn from a vertex to the midpoint of the opposite side of the triangle.
In this context, we can logically deduce that a line segment with end points at the vertex and the midpoint of the triangle's opposite side simply refers to the median of a triangle.
Read more on triangles and line segment here: https://brainly.com/question/30314207
#SPJ1
What is the Domain and range of y=(x-1)^2-4
Answers
Percent decrease of $16 to $4
Answers
Answer:
75% decrease
Step-by-step explanation:
x/100*12/16
x = percent decrease
subtract what you got in the end (4) from the original number (16) to get 12
(12*100) ÷ 16
1200 ÷ 16 = 75% decrease
x = 75%
1.
I Which number line shows the solution to the inequality
-3x - 5 < -2?
A.
B.
C.
D.
-3 -2 -1 0 1
-3 -2 -1 0 1
0++
0 1
3 -2 -1 0
2 3
2 3
2 3
+++
-3 -2 -1 0 1 2 3
Answers
The sum of 25 and 5 times a number is equal to 40.
Answers
Answer:
The equation is 5x+25=40
The answer is x=3
Step-by-step explanation:
The equation is 5x+25=40
Subtract 25 on both sides:
5x=15
Divide 5 on both sides:
x=3
Hope this helps!
solve it by using high order derivative
y=1÷(X+2)(x^2+4)
Answers
Answer:
I think it is ± 2y−2X1 −22y− 2X1−2+4=x2=x
Step-by-step explanation:
hope this helps if not let me know
