Answers
Answer:
x=1.7320508075688...... equal to 1.73
Step-by-step explanation:
equation is: y=x*x+1
so put 4 instead of y
4=x*x+1
so x*x=3
x=1.7320508075688......
Related Questions
What value of x is the solution to 2.5x =8?
Answers
Answer:
x=3.2
Step-by-step explanation:
2.5x=8
divide both sides by 2.5
x=3.2
Answer:
x = 3.2
Step-by-step explanation:
\(2.5x = 8\)
\(2.5x - 2.5 = 8 \div 2.5\)
\(x = 8 \div 2.5\)
\(x = 3.2\)
Determine the dimensions of the rectangle of largest area that can be inscribed in a semicircle of radius 4
Answers
Answer:
The length and width that maximize the area are:
W = 2*√8
L = 2*√8
Step-by-step explanation:
We want to find the largest area of a rectangle inscribed in a semicircle of radius 4.
Remember that the area of a rectangle of length L and width W, is:
A = L*W
You can see the image below to see how i will define the length and the width:
L = 2*x'
W = 2*y'
Where we have the relation:
4 = √(x'^2 + y'^2)
16 = x'^2 + y'^2
Now we can isolate one of the variables, for example, x'
16 - y'^2 = x^'2
√(16 - y'^2) = x'
Then we can write:
W = 2*y'
L = 2*√(16 - y'^2)
Then the area equation is:
A = 2*y'*2*√(16 - y'^2)
A = 4*y'*√(16 - y'^2)
If A > 1, like in our case, maximizing A is the same as maximizing A^2
Then if que square both sides:
A^2 = (4*y'*√(16 - y'^2))^2
= 16*(y'^2)*(16 - y'^2)
= 16*(y'^2)*16 - 16*y'^4
= 256*(y'^2) - 16*y'^4
Now we can define:
u = y'^2
then the equation that we want to maximize is:
f(u) = 256*u - 16*u^2
to find the maximum, we need to evaluate in the zero of the derivative:
f'(u) = 256 - 2*16*u = 0
u = -256/(-2*16) = 8
Then we have:
u = y'^2 = 8
solving for y'
y' = √8
And we know that:
x' = √(16 - y'^2) = √(16 - (√8)^2) = √8
And the dimensions was:
W = 2*y' = 2*√8
L = 2*y' = 2*√8
These are the dimensions that maximize the area.

DETAILS WANEFM7 5.2.004. MY NOTES ASK YOUR TEACHER Solve the LP problem. If no optimal solution exists, indicate whether the feasible region is empty or the objective function is unbounded. (Enter EMPTY if the region is empty. Enter UNBOUNDED if the function is unbounded.) Minimize c = x + 2y subject to x + 3y 223 8x + y 2 23 x3 0, y 20. (x, y) =
Answers
The feasible region is not empty and the objective function is bounded because it achieves its minimum value at the corner point (0, 0). Hence, the solution to the given LP problem is (x, y) = (0, 0).
Given an LP problem Minimize \(c = x + 2y\) subject to the constraints \(x + 3y ≤ 223 8x + y ≤ 23 x ≥ 0, y ≥ 0\)
Now we can start solving this LP problem by drawing the graph for the given constraints :
Plotting the constraints on a graph.
We can see that the feasible region is the shaded region bounded by the lines x = \(0, y = 0, 8x + y = 23, and x + 3y = 223\)
Now we can check the corner points of this region for finding the optimal solution of the given problem.
Corner points of the feasible region are:
(0, 0), (0, 7.67), (2.88, 71.07), (23, 66.33), and (27.33, 65).
Now we can substitute these values of x and y into the objective function \(c = x + 2y\) and see which corner point gives us the minimum value of c.
The table below summarizes this calculation.
Corner point
\((x, y)c = x + 2y\) (0,0)0(0,7.67)15.34(2.88,71.07)145.03(23,66.33)112.67(27.33, 65)157.67.
Thus, we can see that the minimum value of the objective function \(c = x + 2y\) is achieved at (0, 0),
which is one of the corner points of the feasible region.
Therefore, the optimal solution of the given LP problem is \(x = 0\) and \(y = 0\)
Also, we can see that the feasible region is not empty and the objective function is bounded because it achieves its minimum value at the corner point (0, 0).
Hence, the solution to the given LP problem is \((x, y) = (0, 0)\)
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
Executives for a car dealership are interested in the sales for the type of vehicle, SUV or truck, and the type of power train, two-wheel drive (2WD), four-wheel drive (4WD), or all-wheel drive (AWD). The data from the
sales of 165 vehicles are displayed in the two-way table.
A vehicle is randomly selected. Let S be the event that
the vehicle is an SUV and let D be the event that the vehicle has 4WD. What is the value of P(S and Dc)?
O 0.04
O 0.23
O 0.38
O 0.41

Answers
Assuming S is the event that the vehicle is an SUV the value of P(S and D) is:0.38.
ProbabilityNumber of vehicles=165
Total number of SUV=10+23+52=85
Hence:
The event that vehicle is SUV(S)=85
The event that vehicle is 4WD(D)=23
Value of P(S and D)=85-23/165
Value of P(S and D)=62/165
Value of P(S and D)=0.375
Value of P(S and D)=0.38 (Approximately)
Inconclusion the value of P(S and D) is:0.38.
Learn more about probability here:https://brainly.com/question/24756209
Answer:
c) 0.38
Step-by-step explanation:
just answered it
Let X1, . . . ,Xn be independent random variables, each one distributed uniformly on [0, 1].
Let Z be the minimum and W the maximum of these numbers.
Find the joint density function of Z and W.
Answers
The joint density function of Z and W, representing the minimum and maximum of n independent uniformly distributed random variables, involves the factorial term, Jacobian matrix, and the difference between W and Z raised to the power of n-1.
The joint density function of Z and W, where Z represents the minimum and W represents the maximum of n independent random variables X1, ..., Xn, each uniformly distributed on the interval [0, 1], can be described as follows: The joint density function f(Z, W) is equal to n!(n-2)! times the absolute value of the determinant of the Jacobian matrix divided by (W-Z)^(n-1). The joint density function f(Z, W) is zero when Z > W and when either Z or W is outside the interval [0, 1]. Otherwise, it is positive within this region. The joint density function accounts for the ordering of the random variables, ensuring that Z is the minimum and W is the maximum. The Jacobian matrix and its determinant are used to transform the variables and account for the ordering. In summary, It is zero outside the valid interval and accounts for the ordering of the variables.
Learn more about Jacobian matrix here: brainly.com/question/32236767
#SPJ11
plzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz

Answers
Answer:
60 degrees
Step-by-step explanation:
A triangle is 180 degrees and there is already 40 and 80 degrees.
So... 180-80-40=60 degrees.
Hope this helps :D
X+80+40=180
X+120=180
X=180-120
Therefore X=60 degree ans
Hope this helps you!
Please mark it as the brainliest<3
Problem. If-2 f(x) 5 on -1,3 then find upper and lower bounds for J f(a)dz Lower Bound: Upper Bound:
Answers
the upper bound is 20.
the lower bound is - 8.
Given that, -2 ≤ f(x) ≤ 5 on [-1,3].
Evaluate the integral to find the lower and upper bounds:
∫₋₁³f(x) dx
Substitute f(x) =-2 for the lower bound:
∫₋₁³ f(x) dx = ∫₋₁³ (- 2) dx
= [- 2x]₋₁³
= - 6 - 2
= - 8
Therefore, the lower bound is - 8.
Now, substitute f(x) = 5 into the integral for the upper bound:
∫₋₁³ f(x) dx = ∫₋₁³ (-5) dx
= [5x]₋₁³
= 15 + 5
= 20
Therefore, the upper bound is 20.
Learn more about the integrals here
brainly.com/question/18125359
#SPJ4
The given question is incomplete, then complete question is below
If −2≤f(x)≤5 on [−1,3] then find upper and lower bounds for ∫₋₁³f(x)dx
The circumference of the earth is 2.4x109 miles. if you traveled at an average of 8.5x10 miles per hour, how long would it take for you to go around the earth? round your answer to the nearest whole number.
a. 2,820 hours
c. 354 hours
b. 282 hours
d. 3,500 hours
Answers
Answer:
282 hr <======= see below
Step-by-step explanation:
Distance / rate = time
2.4 x 10^9 mi / 85 m/hr = 28235294 hr
You must have left the power of 10 off of your speed
probably should be 8.5 x 10^6 perhaps? then answer is 282
If speed was 8.5 x 10^5 then answer becomes ~ 2820
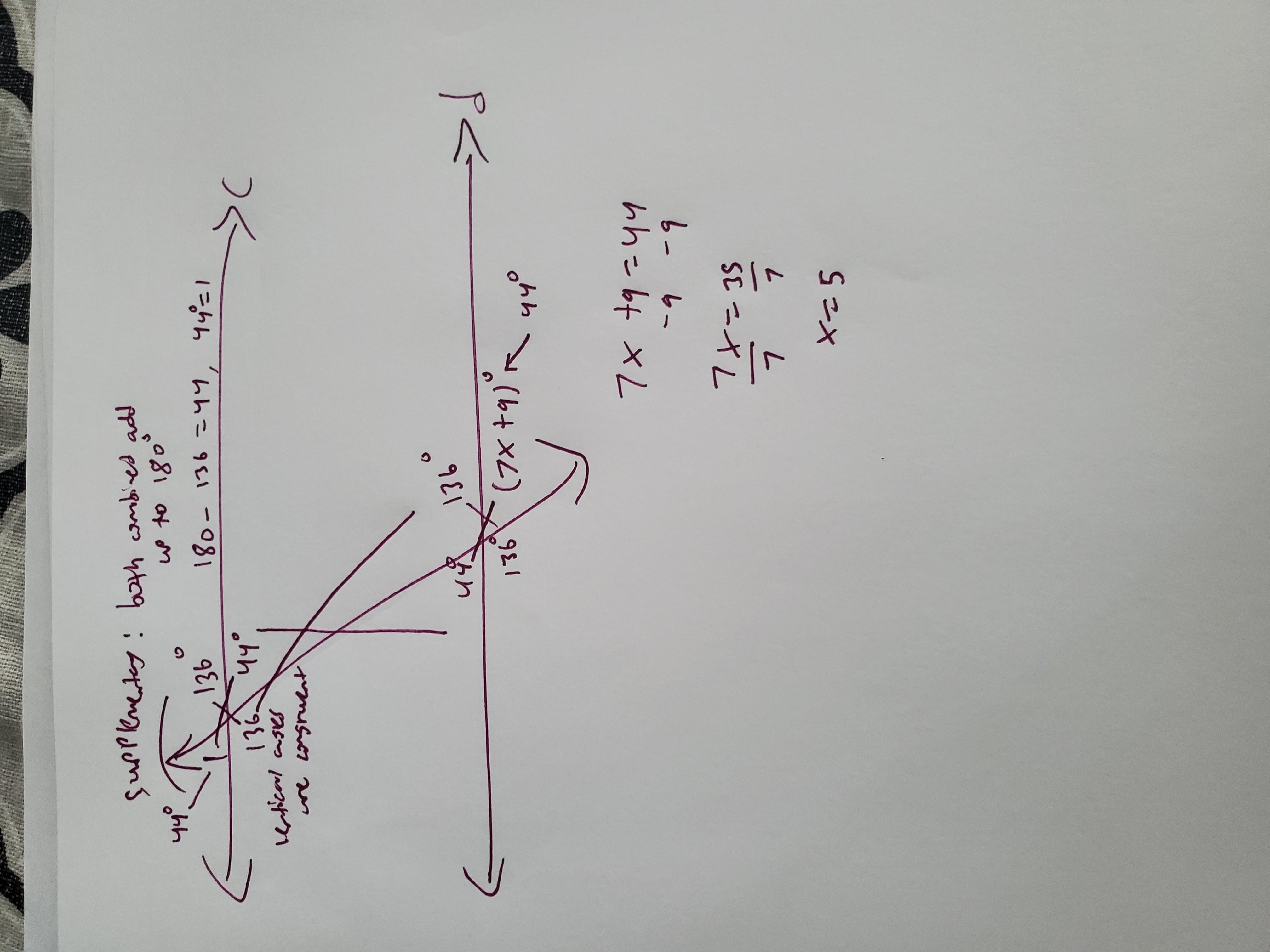
Find the value of x. Show all of your work to earn full credit. DON'T SKIP STEPS!

Answers
Answer: 44 degrees, x equals
Step-by-step explanation: Attached below is my work.
There are 20 members of a basketball team. (a) The coach must select 12 players to travel to an away game. How many ways are there to select the players who will travel
Answers
There are 20 members of a basketball team. (a) The coach must select 12 players to travel to an away game. There are \(\(\binom{20}{12}\)\) ways to select the players who will travel to the away game.
To determine the number of ways to select the players who will travel, we can use the concept of combinations. We want to choose 12 players from a group of 20 players. The notation \(\(\binom{n}{r}\)\) represents the number of ways to choose r objects from a set of n objects without regard to the order of selection. In this case, we want to choose 12 players from a group of 20, so we use the combination formula:
\(\(\binom{20}{12} = \frac{20!}{12!(20-12)!}\)\)
Simplifying the expression, we get:
\(\(\binom{20}{12} = \frac{20!}{12!8!}\)\)
This gives us the total number of ways to select 12 players from a group of 20, which is the answer to the question.
Learn more about combinations here:
https://brainly.com/question/28065038
#SPJ11
A painting is 20 cm wider than the height and 576 cm² write a representation using variable x
Answers
Answer:
For x = height:
x(x + 20) = 576.
Step-by-step explanation:
The area is 576 cm^
Area = width * height
Let the height be x, then the width is (x + 20) cm
So the expression for the area can be written
x(x + 20) = 576.
Answer:
x² + 20x - 576 = 0
Step-by-step explanation:
If x is height:
width = (20 + x)
area = width x height
576 = (20 + x) x x
576 = 20x + x²
∴ x² + 20x - 576 = 0
what is the value of x

Answers
Answer:
x=60
Step-by-step explanation:
this is an isosceles triangle. so angle D and F are equal. D= x and F=x. so 58+x+x=180
2x+58=180
2x=122
x=60
Which statement correctly describes the association between temperature and the number of hikers that reached the overlook?
A.The association is linear because it is negative.
B.The association is negative but not linear.
C.The association is positive but not linear.
D.The association is neither positive nor negative because it is not linear.

Answers
The association is neither positive nor negative because it is not linear. The solution has been obtained by using the concept of linear relationship.
What is linear relationship?
In statistics, a linear relationship is a connection that runs in a straight line between two variables (or linear association).
We know that a linear relationship can be represented mathematically, and graphically, in which the variable and constant are connected by a straight line.
From the figure, we can see that the points are scattered and do not form a straight line.
So, it is not linear.
Hence, the association is neither positive nor negative because it is not linear.
Learn more about linear relationship from the given link
https://brainly.com/question/13828699
#SPJ1
ally and Anne went to the movies. They each purchased a drink. They also bought one popcorn and one veggie cup to share. Each woman’ total is modeled with this expression:
9 + 1.34 +
1
2
(3.50 +1.74)
How would you simplify the expression? Explain your steps.
Answers
Answer:
13.48
Step-by-step explanation:
Rafi has $6,629 in an account that earns 10% interest compounded annually.
To the nearest cent, how much interest will he earn in 4 years?
Answers
The amount of interest would be $3076.51 in the account after 4 years.
What is Compound interest?Compound interest is defined as interest paid on the original principal and the interest earned on the interest of the principal.
A = P(1+r/100)ⁿ
Where:
A = the future value of the investment or loan
P = the principal investment or loan amount
r = the interest rate (decimal)
n = the number of compound periods
Given that Rafi has $6,629 in an account that earns 10% interest compounded annually.
p = $6,629
r = 10%
t = 4 years
A = P(1+r/100)ⁿ
Substitute the values of p,r, and t in the formula,
A = 6,629 (1 + 10/100)⁴
A = 6,629 (1 + 0.10)⁴
A = 6,629 (1.1)⁴
A ≈ 9705.51
Now, C.I. = A - P
So C.I. = 9705.51 - 6,629 = $3076.51
Therefore, the amount of interest would be $3076.51 in the account after 4 years.
To learn more about Compound interest click here:
brainly.com/question/25857212
#SPJ1
2. Why does this
equation have no
solutions?
3(4x12) = 2(6x + 8)
Answers
The equation 3(4x + 12) = 2(6x + 8) has no solution because the variable x was neglected as it equals 0.
How to calculate the value?It should be noted that the equation given is illustrated as:
3(4x + 12) = 2(6x + 8)
Open the parentheses
12x + 36 = 12x + 16
Collect like terms
12x - 12x = 16 - 36
0 = -20
Therefore, it has no solution.
Learn more about equations on:
brainly.com/question/2972832
#SPJ1
Two sides of a trapezoid are shown below. The segment connecting points (-1,5) and (5,5) is a base of the trapezoid.
Draw the two missing sides so that the midsegment has a length of 9 units.
Answers
Answer:
To draw the missing sides of the trapezoid so that the midsegment has a length of 9 units, you can follow these steps:
Plot the given base segment connecting points (-1,5) and (5,5) on a coordinate plane.
Find the midpoint of the given base segment using the midpoint formula: Midpoint = ((x1 + x2)/2, (y1 + y2)/2), where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the given base segment.
Plot the midpoint found in step 2 on the coordinate plane as the midpoint of the midsegment. Label it.
Draw two perpendicular lines from the midpoint found in step 2, each extending towards the other base of the trapezoid.
The intersection points of the perpendicular lines with the other base of the trapezoid will be the vertices of the missing sides.
Connect the vertices of the missing sides with the endpoints of the given base segment to complete the trapezoid.
Note: The specific length and orientation of the missing sides will depend on the location of the midpoint and the given base segment. There can be multiple valid trapezoids with a midsegment of length 9 units that connect the given bases at the midpoint.
Step-by-step explanation:
State what method should be used in solving the followings (either the substitution rule or the integration by parts). Next, evaluate the integrals given.
a. ∫( y^a+1)/√(b+y+cy^(a+1)) dy where a≠0 and c=1/(a+1)
b. ∫t^2cos3t dt
Answers
a. In solving ∫\(( y^{(a+1)})/√(b+y+cy^{(a+1)})\) dy where a≠0 and c=1/(a+1) either substitution rule or integration by parts can be used.
Substitution rule method should be used in solving the integral.
Substituting u = b + y + \(cy^{(a+1)\) will give us;
dy = (1/(a+1)) * \(u^{(-a/2)\) * du
Substituting these into the integral above will give us:
∫ \((y^{(a+1)})/√(b+y+cy^{(a+1)}) dy = (1/(a+1)) ∫ u^{(-a/2)} * (u-b-cy^{(a+1)}) dy = (1/(a+1))\)\(∫ u^{(-a/2)} * u^{(1/2)} du = (1/(a+1)) * 2u^{(1/2 - a/2 + 1)} / (1/2 - a/2 + 1) + C= 2/(a-1) * (b+y+cy^{(a+1)})^{(1/2 - a/2 + 1)} + C\)Where C is the constant of integration.
b. Integration by parts method should be used in solving the integral ∫t^2cos3t dt.
Let; u =\(t^2\) and dv = cos 3t dt
Then; du = 2t dt and v = 1/3 sin 3t
By integration by parts formula we have;
\(∫ t^2cos3t dt = t^2 * (1/3 sin 3t) - ∫ 2t * (1/3 sin 3t) dt= (t^{2/3}) sin 3t - (2/3) ∫ t sin 3t dt\)Using integration by parts method again;
Let u = t and dv = sin 3t dt
Then; du = dt and v = (-1/3) cos 3t
Then;
∫ t sin 3t dt = -t (1/3) cos 3t + ∫ (1/3) cos 3t dt= -t (1/3) cos 3t + (1/9) sin 3t
Using this in the above expression gives;
∫ t²cos3t dt = (\(t^{2/3\)) sin 3t - (2/9) t cos 3t + (2/27) sin 3t + C
Where C is the constant of integration.
To know more about integration visit:
https://brainly.com/question/31744185
#SPJ11
a) Substitution rule
The integral `∫( y^(a+1))/√(b+y+cy^(a+1)) dy` can be solved by the substitution rule. The substitution rule states that given a function `f(u)` and a function `g(x)` such that `f(u)` has an antiderivative,
then `∫f(g(x))g'(x)dx = ∫f(u)du`.
Let `u = b + y + cy^(a + 1)`.Then `du/dy = 1 + c(a + 1)y^a`
.Using the substitution rule:`∫( y^(a+1))/√(b+y+cy^(a+1)) dy = ∫(1 + c(a + 1)y^a)^{-1/2}y^{a+1}dy = 2(1 + c(a+1)y^a)^{1/2} + C`.b) Integration by parts
The integral `∫t^2cos3t dt` can be solved by using integration by parts. The integration by parts formula is given by: `∫u dv = uv - ∫v du` where `u` and `v` are functions of `x`.
Let `u = t^2` and `dv = cos3t dt`.
Then `du = 2t dt` and `v = (1/3)sin3t`.
Using the integration by formula:`∫t^2cos3t dt = (1/3)t^2sin3t - (2/3)∫tsin3t dt = (1/3)t^2sin3t + (2/9)cos3t - (2/27)t sin3t + C`.
To know more about function , visit:
https://brainly.com/question/11624077
#SPJ11
Identify the correct graph of the system of equations.
3x + y = 12
x + 4y = 4
A) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 12.
B) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12.
C) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 12.
D) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12.
Answers
D) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12.
Use Finite-Difference methods to set up the following differential equation between x = 0 and x = 4 with a step size of Δx=1 d²y/dx² = y + 2
Where y(0) = 2 and y(4). = 55. Set up the solution as a matrix. Use the excel sheet to document your matrix and solve.
Answers
y[i] represents the unknown values of y at each grid point, and we have incorporated the boundary conditions y(0) = 2 and y(4) = 55 into the matrix equation.
To set up the given differential equation using finite-difference methods, we'll approximate the second derivative of y with respect to x using a finite difference formula. Let's define a grid with a step size of Δx = 1 and discretize the domain from x = 0 to x = 4.
First, we need to determine the number of grid points. Since we have Δx = 1 and the domain goes from x = 0 to x = 4, we will have 5 grid points (including the endpoints).
Let's label the grid points as follows:
x0 = 0, x1 = 1, x2 = 2, x3 = 3, x4 = 4
Now, we'll approximate the second derivative of y with respect to x using a centered difference formula:
d²y/dx² ≈ (y[i+1] - 2y[i] + y[i-1]) / (Δx)²
Applying this formula at each interior grid point (i = 1, 2, 3), we can write the discretized equation as:
(y[i+1] - 2y[i] + y[i-1]) / (Δx)² = y[i] + 2
Rearranging the equation, we get:
y[i+1] - 2y[i] + y[i-1] = (Δx)² * (y[i] + 2)
To set up the solution as a matrix, we can write the equation for each interior grid point as follows:
For i = 1:
y[2] - 2y[1] + y[0] = (Δx)² * (y[1] + 2)
For i = 2:
y[3] - 2y[2] + y[1] = (Δx)² * (y[2] + 2)
For i = 3:
y[4] - 2y[3] + y[2] = (Δx)² * (y[3] + 2)
Now, we can write the matrix equation as:
| -2 1 0 0 | | y[1] | | (Δx)² * (y[1] + 2) - y[0] |
| 1 -2 1 0 | | y[2] | = | (Δx)² * (y[2] + 2) |
| 0 1 -2 1 | | y[3] | | (Δx)² * (y[3] + 2) |
| 0 0 1 -2 | | y[4] | | (Δx)² * (y[4] + 2) - y[5] |
Here, y[i] represents the unknown values of y at each grid point, and we have incorporated the boundary conditions y(0) = 2 and y(4) = 55 into the matrix equation.
To know more about derivative, visit:
https://brainly.com/question/25324584
#SPJ11
roman spun the spinner 34 times and landed on 4 a total of six times what is romans experimental probability
Answers
Romans experimental probability is 0.176.
What is probability?Probability simply means the likelihood that something will happen or take place.
In this case, Roman spun the spinner 34 times and landed on 4 a total of six time.
The probability will be:
= Number of occurence / Total available value
= 6 / 34
= 0.176
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
The quadratic expression x2−2x−35 can be factored into (x+5)(x−7) . Which ordered pairs represent the zeros of this expression’s related quadratic function?
Answers
Answer:
(-5,0) and (7,0)
Step-by-step explanation:
You are being asked to find "zeros", so just keep in mind that
zeros ARE roots ARE solutions ARE x-intercepts.
(there are tiny, technical differences bc math reasons, but on a simple overview, they are all the same thing!)
Set equal to zero and solve.
see image.
"ordered pairs" means write the answer like a point (x,y) We found the x when y is zero. See image.

A sterilization procedure yields a decimal reduction time of
0.65 minutes. Calculate the minimum sterilization time required to
yield 99.9% confidence of successfully sterilizing 50 L of medium
containing 10^6 contaminating organisms using this procedure.
Answers
The minimum sterilization time required to achieve a 99.9% confidence level in successfully sterilizing 50 L of medium containing 10^6 contaminating organisms is approximately 1.95 minutes.
To calculate the minimum sterilization time required to yield 99.9% confidence of successfully sterilizing 50 L of medium containing 10^6 contaminating organisms, we need to use the concept of decimal reduction time (D-value) and the number of organisms.
The D-value represents the time required to reduce the population of microorganisms by one log or 90%. In this case, the given D-value is 0.65 minutes.
To achieve a 99.9% confidence level, we need to reduce the population of microorganisms by three logs or 99.9%, which corresponds to a 10^-3 reduction.
To calculate the minimum sterilization time, we can use the following formula:
Minimum Sterilization Time = D-value × log10(N0/Nf)
Where:
D-value is the decimal reduction time (0.65 minutes).
N0 is the initial number of organisms (10^6).
Nf is the final number of organisms (10^6 × 10^-3).
Let's calculate it step by step:
Nf = N0 × 10^-3
= 10^6 × 10^-3
= 10^3
Minimum Sterilization Time = D-value × log10(N0/Nf)
= 0.65 minutes × log10(10^6/10^3)
= 0.65 minutes × log10(10^3)
= 0.65 minutes × 3
= 1.95 minutes
Therefore, the minimum sterilization time required to yield 99.9% confidence of successfully sterilizing 50 L of medium containing 10^6 contaminating organisms using this procedure is approximately 1.95 minutes
To learn more about confidence level visit : https://brainly.com/question/15712887
#SPJ11
Suppose that X has a hypergeometric distribution with N = 100, n = 4, and K = 20. Determine the following: a. P(X = 1) b. P(X = 6) c. P(X = 4) d.
Answers
The probabilities for the hypergeometric distribution with the given parameters are:
a. P(X = 1) ≈ 0.000407
b. P(X = 6) = 0
c. P(X = 4) ≈ 0.098117
d. P(X = 0) ≈ 1.97e-05
What is probability?Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty.
To determine the probabilities for the hypergeometric distribution with the given parameters, we can use the following formula:
P(X = k) = (choose(K, k) * choose(N-K, n-k)) / choose(N, n)
where "choose(a, b)" represents the binomial coefficient, calculated as a! / (b! * (a - b)!)
Let's calculate the probabilities:
a. P(X = 1):
P(X = 1) = (choose(20, 1) * choose(100-20, 4-1)) / choose(100, 4)
= (20 * 80) / 3921225
≈ 0.000407
b. P(X = 6):
P(X = 6) = (choose(20, 6) * choose(100-20, 4-6)) / choose(100, 4)
= (38760 * 0) / 3921225
= 0
c. P(X = 4):
P(X = 4) = (choose(20, 4) * choose(100-20, 4-4)) / choose(100, 4)
= (4845 * 80) / 3921225
≈ 0.098117
d. P(X = 0):
P(X = 0) = (choose(20, 0) * choose(100-20, 4-0)) / choose(100, 4)
= (1 * 77) / 3921225
≈ 1.97e-05
Therefore:
a. P(X = 1) ≈ 0.000407
b. P(X = 6) = 0
c. P(X = 4) ≈ 0.098117
d. P(X = 0) ≈ 1.97e-05
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ4
The complete question is:
Suppose that X has a hypergeometric distribution with N = 100, n = 4, and K = 20. Determine the following: a. P(X = 1) b. P(X = 6) c. P(X = 4) d. P(X = 0).
who do I solve this I have only 10 minuted

Answers
Answer:
\(\sum {{n} \atop {1}} \right 6n+2n^2\)
Step-by-step explanation:
Given the series 8 + 12 + 16 + 20+ ...
Sum of nth term Sn = n/2[2a+(n-1)d]
a is the first term = 8
d is the common difference = 12 - 8 = 16 - 12 = 4
Substitute
Sn = n/2[2(8)+(n-1)(4)]
Sn = n/2[16+4n-4]
Sn = n/2[12+4n]
Sn 2n/2[6+2n]
Sn = n(6+2n)
Sn = 6n + 2n²
Hence the sigma representation is expressed as;
\(\sum {{n} \atop {1}} \right 6n+2n^2\)
8+4x≥12
x≤5
x≥1
x≤1
x≥5
Answers
and I dont rlly feel like explaining so yea
The reduced gradient is analogous to the ___________ for linear models.
Answers
The reduced gradient is analogous to the residual for linear models.
In linear regression, the residual represents the difference between the observed values and the predicted values of the dependent variable. Similarly, in optimization, the reduced gradient represents the difference between the current solution and the optimal solution. It is a measure of how far the current solution is from the optimal solution in the direction of the search. By minimizing the reduced gradient, we can move closer to the optimal solution.
The reduced gradient is a widely used optimization technique in non-linear programming that allows for efficient computation of the descent direction at each iteration while accounting for constraints. It involves calculating a partial derivative of the objective function with respect to the variables that are not restricted by the constraints, and then projecting the resulting gradient onto the space defined by the constraints. The resulting vector is called the reduced gradient, and it points in the direction of the steepest descent that is feasible.
for such more question on residual
https://brainly.com/question/22985922
#SPJ11
William bought pencil boxes for his art class. Each box costs $3.50. He gave $30 to the cashier and got $5.50 as change. How many pencil boxes did he buy?
A. 3
B. 4
C. 7
D. 10
Help It's for benchmark testing so I need it now!! D:
Answers
Answer:
D
Step-by-step explanation:
Consider the following non homogeneous differental equation with constant and the parameters 2, 2, 8, σ and p. coefficients at rt = - y" (t) + ay" (t) + by!" (t) + Cy' (t) + dy(t) 3 e + t² (cos (at)
Answers
The given non-homogeneous differential equation can be written as:
- y''(t) + a*y'(t) + b*y(t) + c*y'(t) + d*y(t) = 3*e^t + t^2*cos(at)
To solve this differential equation, we first consider the corresponding homogeneous equation:
- y''(t) + a*y'(t) + b*y(t) + c*y'(t) + d*y(t) = 0
The solutions to the homogeneous equation can be found by assuming a solution of the form y(t) = e^(rt). Substituting this into the equation gives the characteristic equation:
r^2 + (a+c)*r + (b+d) = 0
The roots of the characteristic equation can be found using the quadratic formula:
r = (-b-c ± sqrt((a+c)^2 - 4(b+d))) / 2
Let the roots be denoted as r1 and r2.
If the roots are real and distinct (r1 ≠ r2), then the general solution to the homogeneous equation is:
y(t) = A*e^(r1*t) + B*e^(r2*t)
where A and B are constants determined by initial conditions.
Next, we find a particular solution to the non-homogeneous equation. Since the right-hand side contains terms of the form e^t and t^2*cos(at), we can assume a particular solution of the form:
y_p(t) = Ae^t + B*t^2*cos(at) + C*t^2*sin(at)
where A, B, and C are constants to be determined.
Substituting this particular solution into the non-homogeneous equation, we can solve for the values of A, B, and C.
Once the particular solution is found, the general solution to the non-homogeneous equation is given by the sum of the general solution to the homogeneous equation and the particular solution:
y(t) = y_h(t) + y_p(t)
where y_h(t) represents the general solution to the homogeneous equation and y_p(t) represents the particular solution to the non-homogeneous equation.
To solve the given non-homogeneous differential equation, we need to find the roots of the characteristic equation and determine the general solution to the homogeneous equation. Then, we find a particular solution by assuming a form that matches the right-hand side of the equation and solve for the constants. Finally, the general solution is obtained by adding the general solution to the homogeneous equation and the particular solution.
To know more about differential equation, visit
https://brainly.com/question/1164377
#SPJ11
the graph of y = - square root x is shifted two units up and five units left
Answers
The final transformed function, after shifting two units up and five units left, is y = -√(x + 5) + 2.
To shift the graph of the function y = -√x, two units up and five units left, we can apply transformations to the original function.
Starting with the function y = -√x, let's consider the effect of each transformation:
1. Shifting two units up: Adding a positive constant value to the function moves the entire graph vertically upward. In this case, adding two to the function shifts it two units up. The new function becomes y = -√x + 2.
2. Shifting five units left: Subtracting a positive constant value from the variable inside the function shifts the graph horizontally to the right. In this case, subtracting five from x shifts the graph five units left. The new function becomes y = -√(x + 5) + 2.
The final transformed function, after shifting two units up and five units left, is y = -√(x + 5) + 2.
This transformation affects every point on the original graph. Each x-value is shifted five units to the left, and each y-value is shifted two units up. The graph will appear as a reflection of the original graph across the y-axis, translated five units to the left and two units up.
It's important to note that these transformations preserve the shape of the graph, but change its position in the coordinate plane. By applying these shifts, we have effectively moved the graph of y = -√x two units up and five units left, resulting in the transformed function y = -√(x + 5) + 2.
for more such question on function visit
https://brainly.com/question/11624077
#SPJ8
