‼️‼️I will mark you brainliest‼️‼️
Pls help this is due in 20 mins. Listed in the item bank or key terms and expressions each of which is associated with one of the columns some terms may display additional information when you click on them drag and drop each item to the correct column order does not matter.
(Please tell me what numbers go in what column.) ( I will not take random answers)

Answers
Alternative interior
4 & 6
3 & 5
Corresponding
1 & 5
4 & 7
2 & 6
3 & 8
Alternative
1 & 8
2 & 7
Consecutive
4 & 5
3 & 6
Related Questions
Two business partners jointly own a firm and share equally the revenues. They individually and simultaneously decide how much effort to put into the firm. Let s
1
and s
2
denote the effort choices of partner 1 and partner 2, respectively. Assume s
i
∈[0,4]. The cost of effort is given by s
i
2
for i∈{1,2}. The firm's revenue is given by 4(s
1
+s
2
+bs
1
s
2
) where 0≤b≤
4
1
. (Note that the parameter b reflects the synergies between the effort levels. b>0 implies that the more one partner works, the more productive the other partner is.) The payoffs for partners 1 and 2 are:
u
1
(s
1
,s
2
)=
2
1
[4(s
1
+s
2
+bs
1
s
2
)]−s
1
2
u
2
(s
1
,s
2
)=
2
1
[4(s
1
+s
2
+bs
1
s
2
)]−s
2
2
1 (a) (5 points) Find the best response function of each partner. Draw the best response functions. (b) (5 points) Solve for the Nash equilibrium of this game. (c) (5 points) Now assume that b=−
2
1
. (This implies that the effort levels have negative synergies.) Solve for the best response functions in this case and draw them. (d) (5 points) Solve for the Nash equilibrium of this game. (e) (4 points) Now suppose that the partners can write a contract on effort levels. That is, they can determine the effort levels which would maximize the firm's revenue net of total effort costs. Briefly explain whether you would expect the effort levels they choose to specify in the contract to be higher or lower than the effort levels you found in parts (b) and (d).
Answers
The analysis involves solving optimization problems, graphing best response functions, identifying Nash equilibria, and considering the potential effects of a contract on effort levels
(a) To find the best response functions, we need to determine the effort choices that maximize each partner's payoff given the other partner's effort. This involves optimizing their payoffs by differentiating the utility functions with respect to their effort levels, setting the derivatives equal to zero, and solving for the effort choices. Drawing the best response functions involves plotting the effort choices for each partner as a function of the other partner's effort.
(b) The Nash equilibrium is reached when both partners are choosing their best responses simultaneously. It can be found by identifying the intersection point(s) of the best response functions.
(c) When there are negative synergies (b < 0), the best response functions and their graphical representation will differ from the previous case.
(d) Similar to part (b), the Nash equilibrium for the case with negative synergies is found by identifying the (s) intersection pointof the best response functions.
(e) In this case, where the partners can write a contract on effort levels to maximize the firm's revenue net of total effort costs, the chosen effort levels are likely to be different from the effort levels determined in parts (b) and (d). The contract allows the partners to coordinate their efforts more efficiently by aligning their choices with the overall revenue maximization objective, potentially resulting in higher or lower effort levels compared to the Nash equilibria, depending on the specific contract terms and their impact on synergies.
Learn more about graphs:
https://brainly.com/question/27019155
#SPJ11
Offering 30 points and branliest ‼️‼️‼️ show work

Answers
Dang, I'm only 12 I don't knowwwww
Answer:
hey buddy sorry i dont know the answer hope this help
Step-by-step explanation:
92% of x PLEASE!!!! I NEED HELP
Answers
Answer:
Do you need the fraction form if do its 92/100
what is an equation of the line that passes through the points(-5,1) and(5,-5)?
Answers
\((\stackrel{x_1}{-5}~,~\stackrel{y_1}{1})\qquad (\stackrel{x_2}{5}~,~\stackrel{y_2}{-5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-5}-\stackrel{y1}{1}}}{\underset{run} {\underset{x_2}{5}-\underset{x_1}{(-5)}}}\implies \cfrac{-6}{5+5}\implies \cfrac{-6}{10}\implies -\cfrac{3}{5}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{1}=\stackrel{m}{-\cfrac{3}{5}}(x-\stackrel{x_1}{(-5)}) \implies y-1=-\cfrac{3}{5}(x+5) \\\\\\ y-1=-\cfrac{3}{5}x-3\implies y=-\cfrac{3}{5}x-2\)
A textbook is opened at random. What page numbers is the book opened to if the product of the opened page numbers is 132?
Answers
The book is opened to pages 11 and 12.
How to get the product of the page
So, we can write the equation:x * (x + 1) = 132
Expanding the equation, we get:
x² + x = 132
To solve for x, we need to rewrite the equation as a quadratic equation:
x²+ x - 132 = 0
Now, we can factor the quadratic equation:
(x - 11)(x + 12) = 0
This equation has two solutions for x:
x = 11
x = -12
Since page numbers cannot be negative, we discard the second solution. Thus, the left-hand page number is 11, and the right-hand page number is 11 + 1 = 12.
So, the book is opened to pages 11 and 12.
Read more on product of numbers here : https://brainly.com/question/25301924
#SPJ1
7. Mr. Grover bought a house for ₹30,00,000 in the year 2000. In 2004, the price of that house increased by 10%. In the year 2008, the price increased further by 20%. Calculate the price of the house at the end of 2008.
Answers
The price of the house at the end of 2008 will be 39,60,000
We must determine the price following each rise in order to determine the cost of the house at the end of 2008.
First of all, in 2004 the price jumped by 10%.
10% of 30,00,000 = 0.1 x 30,00,000 = 3,00,000
As a result, the house's new price in 2004 was:
30,00,000 + 3,00,000 = 33,00,000
The price then rose by 20% in 2008.
20% of 33,00,000 = 0.2 x 33,00,000 = 6,60,000
The home's total price at the end of 2008 was therefore: 33,00,000 + 6,60,000 = 39,60,000.
As a result, the house cost 39,60,000 at the end of 2008.
Learn more about price calculation:
https://brainly.com/question/22116936?referrer
3. What is the current price of a common stock that just paid a $4 dividend if it grows 5% annually and investors want a 15% return? (5) ch.7
4(1,05)_4:20 - $42 715-.05 110
4. Redo the preceding problem assuming that the company quits business after 25 years. (5) ch.7
42x 7.05 5. Redo Problem #3 assuming that dividends are constant. (5) 2
Ch.7
=$37,68
4 15 #26.67
6. Redo Problem #3 assuming that dividends are constant and the company quits business after 25 years. (5)
4 x 6.4641 = $25.88
Answers
3. The current price of the common stock is $40.
4. The stock price considering the company quitting business after 25 years is $46.81.
5. The stock price assuming constant dividends is $26.67.
6. The stock price assuming constant dividends and the company quitting business after 25 years is $25.88.
3. The current price of the common stock can be calculated using the dividend discount model. The formula for the stock price is P = D / (r - g), where P is the stock price, D is the dividend, r is the required return, and g is the growth rate. In this case, the dividend is $4, the required return is 15% (0.15), and the growth rate is 5% (0.05). Plugging these values into the formula, we get P = 4 / (0.15 - 0.05) = $40.
4. If the company quits business after 25 years, we need to calculate the present value of the dividends for those 25 years and add it to the final liquidation value. The present value of the dividends can be calculated using the formula PV = D / (r - g) * (1 - (1 + g)^-n), where PV is the present value, D is the dividend, r is the required return, g is the growth rate, and n is the number of years. In this case, D = $4, r = 15% (0.15), g = 5% (0.05), and n = 25. Plugging these values into the formula, we get PV = 4 / (0.15 - 0.05) * (1 - (1 + 0.05)^-25) = $46.81. Adding the final liquidation value, which is the future value of the stock price after 25 years, we get $46.81 + $0 = $46.81.
5. Assuming constant dividends, the stock price can be calculated using the formula P = D / r, where P is the stock price, D is the dividend, and r is the required return. In this case, the dividend is $4 and the required return is 15% (0.15). Plugging these values into the formula, we get P = 4 / 0.15 = $26.67.
6. If the company quits business after 25 years and assuming constant dividends, we need to calculate the present value of the dividends for those 25 years and add it to the final liquidation value. The present value of the dividends can be calculated using the formula PV = D / r * (1 - (1 + r)^-n), where PV is the present value, D is the dividend, r is the required return, and n is the number of years. In this case, D = $4, r = 15% (0.15), and n = 25. Plugging these values into the formula, we get PV = 4 / 0.15 * (1 - (1 + 0.15)^-25) = $25.88. Adding the final liquidation value, which is the future value of the stock price after 25 years, we get $25.88 + $0 = $25.88.
To know more about the dividend discount model, refer here:
https://brainly.com/question/32294678#
#SPJ11
let y=ln(x2 y2). determine the derivative y′ at the point (e5−25,5).
Answers
To find the derivative of y=ln(x^2y^2) at (e^5-25,5), use the chain rule and product rule of differentiation. Rewrite the equation, find the partial derivatives dx/dt and dy/dt, and plug in the values to get the derivative of 0.
To find the derivative y′ of y=ln(x^2y^2) at the point (e^5-25,5), we need to use the chain rule and product rule of differentiation.
First, we can rewrite the equation y=ln(x^2y^2) as:
y=2ln|x|+2ln|y|
Then, taking the derivative of each term using the chain rule and product rule:
y' = 2(1/x)(dx/dt) + 2(1/y)(dy/dt)
where dx/dt and dy/dt are the partial derivatives of x and y with respect to some parameter t (which is not given in the question, but we can assume it is time t).
At the point (e^5-25,5), we can plug in the values for x and y:
x = e^(5-25) = e^(-20)
y = 5
Now, we need to find the partial derivatives dx/dt and dy/dt. From the equation x^2y^2 = e^(10), we can take the logarithm of both sides:
ln(x^2y^2) = 10
Using implicit differentiation, we get:
(2x*dx/dt + 2y*dy/dt)/(x^2y^2) = 0
Rearranging and substituting the values for x and y, we get:
dx/dt = -y/x * dy/dt = -5/e^20 * dy/dt
Next, we can find dy/dt by differentiating the equation y = 5 with respect to t:
dy/dt = 0
Finally, we can plug in these values into the derivative formula to get:
y' = 2(1/x)(dx/dt) + 2(1/y)(dy/dt)
= 2(1/e^-20)(-5/e^20*0) + 2(1/5)(0)
= 0
Therefore, the derivative y′ of y = ln(x^2y^2) at the point (e^5-25,5) is 0.
Read more about derivative: https://brainly.com/question/23819325
#SPJ11
Angle EFG is 80
Find side of angle x
Answers
80+2x=180
2x=180-80
2x=100
x=100/2
x=50
HELPPPPPPPPPPPPPPPPppp
What is the constant of proportionality of this sentence? Sarah bought 3 pounds of grapes for $2.25. Ban bought 4 pounds of grapes for $3.00.
Answers
Answer:
75
Step-by-step explanation:
Each pound costs 75¢ so by each pound it increases by 75¢
I rlly need help thanks the question is in the picture

Answers
Answer:
350
Step-by-step explanation:
2500×14%=350000000000000
3. Gridtown USA, besides having excellent donut shops, is known for its precisely laid out grid of streets and avemues. Streets run east-west, and avenues north-south, for the entire stretch of the town, never curving and never interrupted by parks or schools or the like. Suppose you live on the corner of 3rd and 3rd and work on the corner of 12th and 12th. Thus travel 18 blocks to get to work as quickly as possible. (a) How many different routes can you take to work, assuming you want to get there as quickly as possible? Explain. you must (b) Now suppose you want to stop and get a donut on the way to work, from your favorite donut shop on the corner of 10th ave and 8th st. How many routes to work, stopping at the donut shop, can you take (again, ensuring the shortest possible route)? Explain. (c) Disaster Strikes Gridtown: there is a pothole on 4th ave between 5th st and 6th st. How many. routes to work can you take avoiding that unsightly (and dangerous) stretch of road? Explain. (d) The pothole has been repaired (phew) and a new donut shop has opened on the corner of 4th ave and 5th st. How many routes to work drive by one or the other (or both) donut shops? Hint: the donut shops serve PIE.
Answers
There are 4 possible routes to work that pass by one or both donut shops.
How to count paths on a grid and avoid certain edges on a graph?
(a) To travel from 3rd and 3rd to 12th and 12th in the shortest distance possible, you can only move east or north. Since you need to travel 18 blocks, you must travel 12 blocks east and 6 blocks north or 6 blocks east and 12 blocks north. This gives two different possible routes.
(b) To get a donut on the way to work, you can take one of two possible routes to the donut shop on the corner of 10th ave and 8th st, and then take one of two possible routes from the donut shop to work. This gives a total of 2 × 2 = 4 possible routes.
(c) If you need to avoid the stretch of 4th ave between 5th st and 6th st, then you can only move east or north until you reach 4th ave. Once you reach 4th ave, you can either move north or south of the pothole, but not through it.
Thus, you can take one of two possible routes to 4th ave, and then one of two possible routes north or south of the pothole, and then one of two possible routes from 4th ave to work. This gives a total of 2 × 2 × 2 = 8 possible routes.
(d) To pass by one or both donut shops, you can take the following routes:
Route 1: Go east on 3rd St to 4th Ave, then north on 4th Ave to 5th St, then east on 5th St to 10th Ave, then north on 10th Ave to 12th St.
Route 2: Go east on 3rd St to 10th Ave, then north on 10th Ave to 8th St, then west on 8th St to 4th Ave, then north on 4th Ave to 5th St, then east on 5th St to 12th Ave.
Route 3: Go east on 3rd St to 4th Ave, then north on 4th Ave to 5th St, then east on 5th St to 8th Ave, then south on 8th Ave to 10th St, then west on 10th St to 12th Ave.
Route 4: Go east on 3rd St to 10th Ave, then north on 10th Ave to 12th St.
Thus, there are 4 possible routes to work that pass by one or both donut shops.
Learn more about combinatorics and graph theory
brainly.com/question/31293479
#SPJ11
Please Help!!! Compare continuous functions f, g, and h, and match the statements with the function they best describe.
Drag each description to the correct location on the table.

Answers
Answer: Not sure if this is 100% correct, but it should be.
Step-by-step explanation:

Assume that all grade point averages are to be standardized on a scale between 0 and 4. How many grade-point averages must be obtained so that the sample mean is within .02 of the population mean
Answers
Therefore, we would need to obtain at least 9604 grade-point averages to ensure that the sample mean is within 0.02 of the population mean with 95% confidence.
To determine the required sample size, we need to use the formula n = [(z * σ) / E]^2, where z is the z-score for the desired level of confidence (e.g. 1.96 for 95%), σ is the standard deviation of the population (which we don't know, so we can use a conservative estimate of 1), and E is the desired margin of error (0.02 in this case). Plugging in these values, we get n = [(1.96 * 1) / 0.02]^2 = 9604. So we would need to obtain at least 9604 grade-point averages to ensure that the sample mean is within 0.02 of the population mean with 95% confidence.
To determine the required sample size for standardizing grade point averages on a scale between 0 and 4 with a margin of error of 0.02, we can use the formula n = [(z * σ) / E]^2, where z is the z-score for the desired level of confidence, σ is the standard deviation of the population, and E is the desired margin of error. Assuming a 95% confidence level and a conservative estimate of σ = 1, we find that we would need at least 9604 grade-point averages to ensure that the sample mean is within 0.02 of the population mean.
Therefore, we would need to obtain at least 9604 grade-point averages to ensure that the sample mean is within 0.02 of the population mean with 95% confidence.
To learn more about the average visit:
https://brainly.com/question/20118982
#SPJ1
only need help on 38 please

Answers
Answer: D
Step-by-step explanation:
solve the system or equations by substitution
y= 3
2x- y = 7
Answers
2x=7+3
-2x=10
X=-5
explanation: u have to move all the terms that don’t contain X to the right then solve
Match each scenario involving projectile motion with the equation that describes the height of the object at time t. Tiles h = -4.9t2 + 5 h = -4.9t2 + 1.5 h = -16t2 + 73t + 1.5 h = -16t2 + 5 h = -16t2 + 73t + 5 h = -4.9t2 + 73t + 1.5 Pairs Dwayne throws a ball with an initial velocity of 73 feet/second. Dwayne holds the ball 5 feet off the ground before throwing it. A watermelon falls from a height of 5 feet to splatter on the ground below. Marcella shoots a foam dart at a target. She holds the dart gun 1.5 meters off the ground before firing. The dart leaves the gun traveling 73 meters/second. Greg drops a life raft off the side of a boat 1.5 meters above the water.
Answers
Answer:
h = -16t^2 + 73t + 5h = -16t^2 + 5h = -4.9t^2 + 73t + 1.5h = -4.9t^2 + 1.5Step-by-step explanation:
The general equation we use for ballistic motion is ...
\(h(t)=\frac{1}{2}gt^2+v_0t+h_0\)
where g is the acceleration due to gravity, v₀ is the initial upward velocity, and h₀ is the initial height.
The values of g commonly used are -32 ft/s², or -4.9 m/s². Units are consistent when the former is used with velocity in ft/s and height in feet. The latter is used when velocity is in m/s, and height is in meters.
_____
Dwayne throws a ball with an initial velocity of 73 feet/second. Dwayne holds the ball 5 feet off the ground before throwing it. (h = -16t^2 + 73t + 5)
A watermelon falls from a height of 5 feet to splatter on the ground below. (h = -16t^2 + 5)
Marcella shoots a foam dart at a target. She holds the dart gun 1.5 meters off the ground before firing. The dart leaves the gun traveling 73 meters/second. (h = -4.9t^2 + 73t + 1.5)
Greg drops a life raft off the side of a boat 1.5 meters above the water. (h = -4.9t^2 + 1.5)
_____
Additional comment on these scenarios
The dart and ball are described as being launched at 73 units per second. Generally, we expect launches of these kinds of objects to have a significant horizontal component. However, these equations are only for vertical motion, so we must assume the launches are straight up (or that the up-directed component of motion is 73 units/second).
(b) Find the basis and dimension for the null space of the linear transformation. Where the linear transformation T: R3 R3 defined as T(x, y, z) = (-2x + 2y + 2z, 3x + 5y + z, 2y+z)
Answers
The basis for the null space is {[1, 0, 1], [1, -1, 0]}, and the dimension of the null space is 2.
To find the basis and dimension for the null space of the linear transformation T: R^3 -> R^3 defined as T(x, y, z) = (-2x + 2y + 2z, 3x + 5y + z, 2y + z), we need to solve the homogeneous equation T(x, y, z) = (0, 0, 0).
Setting each component of T(x, y, z) equal to zero, we get the following system of equations:
-2x + 2y + 2z = 0
3x + 5y + z = 0
2y + z = 0
To solve the system, we can use row reduction or Gaussian elimination. Let's use Gaussian elimination:
Write the augmented matrix:
[ -2 2 2 | 0 ]
[ 3 5 1 | 0 ]
[ 0 2 1 | 0 ]
Perform row operations to obtain the reduced row echelon form:
[ 1 -1 -1 | 0 ]
[ 0 1 1 | 0 ]
[ 0 0 0 | 0 ]
Express the system of equations corresponding to the reduced row echelon form:
x - y - z = 0
y + z = 0
Solve for the variables in terms of a free variable:
x = y + z
y = -z
Express the solution as a vector:
[x, y, z] = [y + z, y, z] = [y + z, -z, z] = z[1, 0, 1] + y[1, -1, 0]
The solution indicates that any vector in the null space of T can be written as a linear combination of the vectors [1, 0, 1] and [1, -1, 0]. Therefore, the basis for the null space is {[1, 0, 1], [1, -1, 0]}, and the dimension of the null space is 2.
learn more about null space here
https://brainly.com/question/27959040
#SPJ11
help me I'm bout to breakdown on this and cry help I'm rlly not ok

Answers
Answer:
বাংলা ৬ নাম্বার প্রশ্নের উওর টা কি
Answer: 3/5 is the correct answer
What are the slope and y-intercept of the linear function shown in the grid?
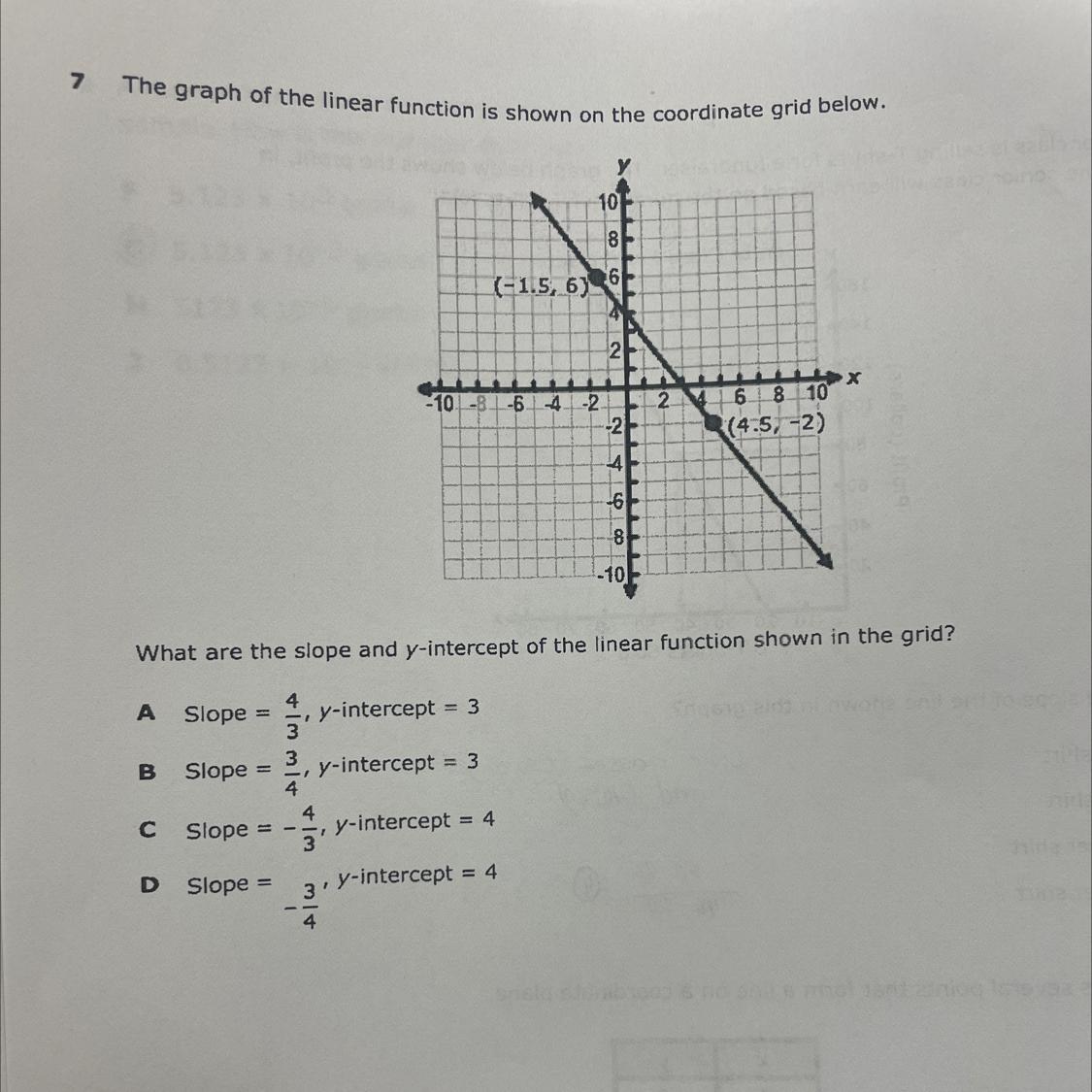
Answers
Answer:
C Slope = -4/3, Y-Intercept = 4
Step-by-step explanation:
The Y- Intercept is where the line contacts the Y-Axis (the vertical line)
Since the line is going down, the slope is going to be negative. You fine the slope by finding a point the line goes through perfectly and then since its negative, go down however many it is until the line goes through another point perfectly, then go right and how many points it takes to get to the point is your denominator. (so your slope is -4/3)
A bicycle tire is 28 inches in diameter. Approximately how far does the bicycle move forward each time the wheel goes around? (use 22/7 as an approximation for pi)
Answers
Answer: 88 inches
Step-by-step explanation:
A bicycle tire is 28 inches in diameter. approximately.
To find the distance traveled by the bicycle each time the wheel goes around we need to find the circumference of the tire.
The circumference of a circle: where d is the diameter of the circle.
Now, the circumference of the tire:
Hence, the distance traveled by the bicycle each time the wheel goes around =88 inches.
A person can read 24 pages of a book in 1/3 of an hour. What is this person's reading rate in pages per hour?
72
48
12
8
Answers
20 mins - 24 pages
hour (60 mins) - 24x3 = 72
At the beginning of the school year, Jamie had $500 in her savings account. She wants to have at least $200 left in the account at the end of the school year. Each week, she withdraws $30 for spending money. To determine how many weeks she can spend $30, Jamie wrote and solved this inequality.
Answers
The mistake she had done is she should have reversed the inequality as per the division property of inequality.
What is inequality?A statement of an order relationship—greater than, greater than or equal to, less than, or less than or equal to—between two numbers or algebraic expressions.
The inequality is:
500 − 30x ≥ 200 −500 −500 −30x ≥ −300 x ≥ 10
Given:
Jamie had $500 in her savings account.
She wants to have at least $200 left in the account at the end of the school year.
The inequality she had done is
500 − 30x ≥ 200 −500 −500 −30x ≥ −300 x ≥ 10
But when she was dividing she should have reversed the inequality as per the division property of inequality.
Learn more about this concept here:
https://brainly.com/question/18648781
#SPJ1
344 thousands x 1/10 compare decimal place vaule
Answers
To compare the decimal place value in the expression 344 thousands x 1/10, we need to consider the concept of place value and how it applies to decimals.Therefore, the decimal place value of the expression has decreased by one place.
In the expression, 344 thousands represents a number in the thousands place. The decimal fraction 1/10 represents a number that is less than one and falls in the tenths place. To compare the decimal place value, we can convert 344 thousands to its decimal equivalent. Since one thousand is equal to 1000, we can rewrite 344 thousands as 344,00 Now, let's consider the decimal place value. The decimal fraction 1/10 represents one-tenth, which is equivalent to moving one place to the right from the ones place.Comparing the decimal place value, we can see that 344 thousands x 1/10 is equal to 34,400.
learn more about consider here:
https://brainly.com/question/13947700
#SPJ11
Assume that Xn are independent and uniform on [0,1]. Let Sn = X₁ + X₂ +...Xn. Compute approximately (using CLT), P(S200 ≤ 90). Solution: 0.0071
Answers
P(S200 ≤ 90) ≈ P(Z ≤ -5/√(200/12)) ≈ 0.0001. So, the approximate value of P(S200 ≤ 90) is 0.0001 which can also be expressed as 0.0071 after rounding it off to 4 decimal places.
Given the following assumptions: Xn are independent and uniform on [0, 1] and Sn = X1 + X2 +...Xn. The goal is to compute P(S200 ≤ 90) approximately by using CLT (Central Limit Theorem).
We know that the Central Limit Theorem states that the sum of independent and identically distributed (iid) random variables with finite variance, when the number of random variables goes to infinity, approaches the standard normal distribution with mean μ and variance σ².
For a uniform distribution, the mean (μ) and variance (σ²) are:
μ = (b + a)/2= (1 + 0)/2
= 1/2σ²
= (b - a)²/12
= (1 - 0)²/12
= 1/12
Thus, for Sn = X1 + X2 +...Xn, we have μ = nμ
= n/2 and σ²
= nσ²
= n/12.
The standardized random variable for S200 is:
Z = (S200 - μ) / (σ / √n)
= (S200 - 100) / (√(200/12))
Now, we have:
P(S200 ≤ 90) = P((S200 - 100) / (√(200/12)) ≤ (90 - 100) / (√(200/12)))
= P(Z ≤ -5/√(200/12))
We look at the standard normal distribution table, the area to the left of -5 is almost 0 (less than 0.0001).
Therefore,
P(S200 ≤ 90) ≈ P(Z ≤ -5/√(200/12))
≈ 0.0001.
So, the approximate value of P(S200 ≤ 90) is 0.0001 which can also be expressed as 0.0071 after rounding it off to 4 decimal places.
Know more about decimal places here:
https://brainly.com/question/28393353
#SPJ11
725 tickets were sold for a game for a total of $1,200.00. if adult tickets sold for $2.00 and children's tickets sold for $1.50, how many of each kind of ticket were sold?
Answers
If adult tickets sold for $2.00 and children's tickets sold for $1.50, 225 adult tickets and 500 children's tickets were sold.
Let x be the number of adult tickets sold and y be the number of children's tickets sold. We can set up a system of equations to represent the given information:
x + y = 725 (equation 1)
2x + 1.5y = 1200 (equation 2)
In equation 1, we know that the total number of tickets sold is 725. In equation 2, we know that the total revenue from ticket sales is $1200, with adult tickets selling for $2.00 each and children's tickets selling for $1.50 each.
To solve for x and y, we can use either substitution or elimination method. Here, we will use the elimination method.
Multiplying equation 1 by 2, we get:
2x + 2y = 1450 (equation 3)
Subtracting equation 3 from equation 2, we get:
-0.5y = -250
Solving for y, we get:
y = 500
Substituting y = 500 into equation 1, we get:
x + 500 = 725
Solving for x, we get:
x = 225
To learn more about equation click on,
https://brainly.com/question/15375043
#SPJ4
How can we find the actual area of a region represented on the map?
Answers
Answer:
A 1 cm by 1 cm square on the map represents a 180,000 cm by 180,000 cm region of land. That is, a 1,800 m by 1,800 m region of land. Its area is 3,240,000 square meters (1,800 times 1,800 is 3,240,000).
Step-by-step explanation:
3. A function can have zero to many parameters, and it can return this many values.a. zero to manyb. noc. only oned. a maximum of tene. None of these
Answers
A function can have zero to many parameters, and it can return only one (option c).
In mathematics, a function is a rule that maps each element from one set, called the domain, to a unique element in another set, called the range.
The number of parameters a function can take determines the number of arguments required to call the function.
For instance, a function f(x) takes one parameter, and it requires one argument to be called.
On the other hand, a function g(x,y,z) takes three parameters, and it requires three arguments to be called. However, a function h() takes no parameters and does not require any argument to be called.
Hence the correct option is (c).
To know more about function here
https://brainly.com/question/28193995
#SPJ4
The rate of snowfall during a recent snowstorm was 1 2 inch per hour. At this rate, how many hours did 7 1 2 inches of snow take to fall?'
Answers
15 hours.
(please mark me as brainlest.)
Answer:
15 hours
Step-by-step explanation:
I'll assume "1 2" is 1/2 and "7 1 2" is 7 1/2.
We can make this into an equation by using x for hours and 1/2 as the rate and set it equal to 7 1/2 to find x.
1/2x=7 1/2
Divide each side of the equation by 1/2.
x=15
SO it took 15 hours for 7 1/2 inches of snow to fall
One firefly flashes every 8 seconds. Another firefly flashes every 10 seconds. Both fireflies just flashed. After how many second will both fireflies flash at the same time again? (I know it's somehow related to LCM, GCF, Prime factorization)
Answers
Answer:
Step-by-step explanation:
You're correct that this problem involves finding the least common multiple (LCM) of 8 and 10, which will give us the number of seconds after which both fireflies will flash at the same time again.
To find the LCM of 8 and 10, we can use their prime factorizations:
8 = 2^3
10 = 2 × 5
The LCM of 8 and 10 is the product of the highest powers of all the prime factors involved, which in this case are 2^3 and 5. Therefore:
LCM(8, 10) = 2^3 × 5 = 40
So after 40 seconds, both fireflies will flash at the same time again. We can check this by dividing 40 by each of the individual flash intervals to see if we get a whole number:
40 ÷ 8 = 5
40 ÷ 10 = 4
Both of these divisions result in whole numbers, which confirms that 40 is the least common multiple of 8 and 10. Therefore, both fireflies will flash at the same time again after 40 seconds.
Answer:
40 sec
Step-by-step explanation:
So here we want to find the LCM of 8 and 10
➝ 8 = 2×2×2 = 2³
➝ 10 = 2×5
LCM(8,10) = 2³×5 = 40
So they will flash again after 40 sec.