Identify the common difference: d=
Identify the zero term(starting amount) a=

Answers
The formula to find the common difference of an arithmetic sequence is: d = a(n) - a(n - 1), where a(n) is a term in the sequence, and a(n - 1) is its previous term in the sequence
What is arithmetic sequence?
A series of numbers called an arithmetic progression or arithmetic sequence has a constant difference between the terms. For instance, the number sequence 5, 7, 9, 11, 13, and 15 has a common difference of 2 in arithmetic.
Sequences can in fact begin at any number that we choose. A sequence with the general word an is commonly notated as ann=1 a n n = 1.
or d = (an + 1 - an) (an – an-1). AP reduces if the common difference is negative. For instance, the AP drops in these numbers: -4, -6, -8.
To learn more about arithmetic sequence visit
https://brainly.com/question/15412619
#SPJ1
Related Questions
Using an example, outline the steps involved in performing a
Wald test to test significance of a sub-group of coefficients in a
multiple regression model.
Answers
The Wald test is a statistical test that can be used to test the significance of a group of coefficients in a multiple regression model.
The test statistic is calculated as the ratio of the estimated coefficient to its standard error. If the test statistic is significant, then the null hypothesis that the coefficient is equal to zero can be rejected.
Suppose we have a multiple regression model with three independent variables: age, gender, and education. We want to test the hypothesis that the coefficients for age and education are both equal to zero. The Wald test statistic would be calculated as follows:
Test statistic = (Estimated coefficient for age) / (Standard error of estimated coefficient for age) + (Estimated coefficient for education) / (Standard error of estimated coefficient for education)
If the test statistic is significant, then we can reject the null hypothesis that the coefficients for age and education are both equal to zero. This would mean that there is evidence that age and education are both associated with the dependent variable.
The Wald test is a powerful tool that can be used to test the significance of a group of coefficients in a multiple regression model. However, it is important to note that the test statistic is only valid if the assumptions of the multiple regression model are met. If the assumptions are not met, then the p-value of the Wald test may be inaccurate.
Here are some of the assumptions of the multiple regression model:
* The independent variables are independent of each other.
* The dependent variable is normally distributed.
* The errors are normally distributed.
* The errors have constant variance.
If any of these assumptions are not met, then the Wald test may not be accurate.
Learn more about multiple regression model here:
brainly.com/question/32816836
#SPJ11
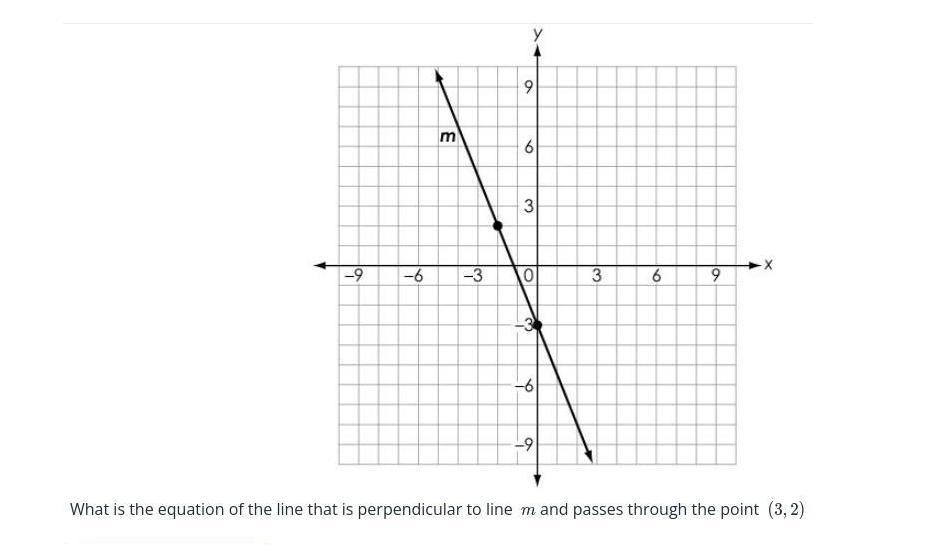
what is the equation of the line that is perpendicular to line m and passes through the point (3,2)
Answers
The equation of the line that is perpendicular to line m and passes through the point (3, 2) is y = (2/5)x + 4/5.
How to Find the Equation of Perpendicular Lines?To find the equation of a line that is perpendicular to line m, we need to know the slope of line m.
The slope of line m can be found using the two given points on the line, (0, -3) and (-2, 2):
slope of line m = (change in y) / (change in x) = (2 - (-3)) / (-2 - 0) = 5 / (-2) = -5/2
A line perpendicular to m will have a slope that is the negative reciprocal of -5/2. The negative reciprocal is obtained by flipping the fraction and changing its sign.
slope of line perpendicular to m = -1 / (-5/2) = 2/5
Now we have the slope of the line perpendicular to m and a point that it passes through, (3, 2). We can use the point-slope form of the equation of a line to find its equation:
y - y1 = m(x - x1), where (x1, y1) is the given point and m is the slope.
Substituting in the values we have:
y - 2 = (2/5)(x - 3)
Simplifying:
y - 2 = (2/5)x - (6/5)
y = (2/5)x - (6/5) + 2
y = (2/5)x + 4/5
Learn more about equation of perpendicular lines on:
https://brainly.com/question/7098341
#SPJ1
Find the length of the line segment joining pair of points ( 4, -1) and (5, 5)

Answers
Answer:
b I believe I just take it
What is the probability of drawing two blue cards if the first one is replaced before the second draw? Assume the first is blue.

Answers
Answer: 1/15
Step-by-step explanation: the answer on Acellus is 1/15
Write the rule to describe the transformation.

Answers
Answer:
Dilation of 3
Step-by-step explanation:
Note \(DE=2\) and \(D'E'=6\).
The scale factor is defined as the ratio of the length of the side of the image to the length of the corresponding side of the preimage.
So, the scale factor is \(\frac{6}{2}=3\).
Select the correct answer. What is the solution to the equation? A. -3 B. 6 C. 7 D. 25
Answers
Answer:
The value of x is 7 if the equation can be reduced to (x + 9)³ = 4096 after applying the properties of the integer exponent option (C) 7 is correct.
What is an integer exponent?
In mathematics, integer exponents are exponents that should be integers. It may be a positive or negative number. In this situation, the positive integer exponents determine the number of times the base number should be multiplied by itself.
It is given that:
The equation is:
After solving:
(x + 9)³ = 4096
x + 9 = ∛4096
x + 9 = 16
x = 7
Thus, the value of x is 7 if the equation can be reduced to (x + 9)³ = 4096 after applying the properties of the integer exponent option (C) 7 is correct.
solve for n -8 = 6+n
Answers
Answer:
no solution
Step-by-step explanation:
n -8 = 6+n
Subtract n from each side
n-n -8 = 6+n-n
-8 = 6
This is never true so there is no solution
Answer:
n = -14
Explanation:
-8 = 6 + n
move n over to the left side of the equation
-8 - n = 6
-8 - (-14) = 6
Prove the following statement using mathematical induction. Do not derive it from Theorem 5.2.1 or Theorem 5.2.2. For every integer n ≥ 1,1 + 6 + 11 + 16 + ... + (5n - 4) = n (5n - 3)/2
Proof (by mathematical induction): Let P(n) be the equation 1 + 6 + 11 + 16 + ... + (5n - 4) = n(5n - 3)/2
We will show that P(n) is true for every integer n ≥ 1
Answers
We have shown that P(1) is true and that if P(k) is true, then P(k+1) is also true. Therefore, by mathematical induction, P(n) is true for every integer n ≥ 1:
1 + 6 + 11 + 16 + ... + (5n - 4) = n(5n - 3)/2.
Basis step: For n = 1, we have:
1 = 1(5(1) - 3)/2
which is true. Therefore, P(1) is true.
Inductive hypothesis: Assume that P(k) is true for some arbitrary positive integer k. That is,
1 + 6 + 11 + 16 + ... + (5k - 4) = k(5k - 3)/2
Inductive step: We need to show that P(k+1) is true, which means we need to show that:
1 + 6 + 11 + 16 + ... + (5(k+1) - 4) = (k+1)(5(k+1) - 3)/2
Starting with the left-hand side of this equation, we have:
1 + 6 + 11 + 16 + ... + (5(k+1) - 4)
= [1 + 6 + 11 + 16 + ... + (5k - 4)] + (5(k+1) - 4)
Using the inductive hypothesis, we can simplify the first part of this expression
[1 + 6 + 11 + 16 + ... + (5k - 4)] = k(5k - 3)/2
Substituting this expression into the equation above, we get:
1 + 6 + 11 + 16 + ...+ (5(k+1) - 4) = k(5k - 3)/2 + (5(k+1) - 4)
Simplifying this expression, we get:
1 + 6 + 11 + 16 + ... + (5(k+1) - 4) = (5k^2 + 7k + 2) / 2
Now, let's simplify the right-hand side of the equation we want to prove:
(k+1)(5(k+1) - 3)/2 = (5k^2 + 13k + 6) / 2
(5k^2 + 7k + 2) / 2 = (5k^2 + 13k + 6) / 2
Simplifying this expression, we get:
k^2 + 3k + 2 = k^2 + 3k + 2
which is true. Therefore, P(k+1) is true.
To know more about mathematical induction, visit:
brainly.com/question/29503103
#SPJ11
What is the solution to the system graph below? ( ;∀;)

Answers
Answer:
(-4,-1)
Step-by-step explanation:
The solution to a system of linear equations is simply where the two lines intersect.
From the graph, we can see that they intersect at (-4,-1).
Therefore, the solution to the system graphed below is (-4,-1).
And we're done!
A company blends two gasolines from High-Quality Fuels and Junk Petroleum (inputs) into two commercial products, Super and Regular gasoline (outputs). For the inputs, the octane ratings, the lead content in grams per litre, and the amounts available in cubic metres (m 3
) and their prices are known. These are: For the Super and Regular gasolines the requirements are: We define the variables as follows: H and J are respectively the amount of gasoline in m 3
purchased from High-Quality Fuels/Junk Petroleum. S and R are respectively the amount of Super/Regular gasoline in m 3
blended and sold. HS, HR, JS, and JR are respectively the amounts in m 3
of High-Quality/Junk gasoline used to make Super/Regular gasoline. For this and each of the other four questions which follow, make sure that you answer parts (a), (b), and (c) as given at the bottom of the previous page.
Answers
Answer:
ok, here is your answer
Step-by-step explanation:
As the question and information provided do not have a specific part (a), (b), and (c) to be answered, I will provide a general approach to solving this problem.
Let's define the objective function and constraints of the given problem.
Objective function: To minimize the cost of producing Super and Regular gasoline
Cost = (price of High-Quality Fuel * amount purchased from High-Quality Fuel) + (price of Junk Petroleum * amount purchased from Junk Petroleum) + (cost of blending Super gasoline) + (cost of blending Regular gasoline)
Constraints:
- The total amount of Super gasoline produced should be less than or equal to the total amount of gasoline purchased
- The total amount of Regular gasoline produced should be less than or equal to the total amount of gasoline purchased
- The amount of High-Quality Fuel used to produce Super gasoline should be less than or equal to the total amount of High-Quality Fuel purchased
- The amount of Junk Petroleum used to produce Super gasoline should be less than or equal to the total amount of Junk Petroleum purchased
- The amount of High-Quality Fuel used to produce Regular gasoline should be less than or equal to the total amount of High-Quality Fuel purchased
- The amount of Junk Petroleum used to produce Regular gasoline should be less than or equal to the total amount of Junk Petroleum purchased
- The octane rating of Super gasoline should be greater than or equal to 96
- The octane rating of Regular gasoline should be greater than or equal to 87
- The lead content of Super gasoline should be less than or equal to 0.5 grams per litre
- The lead content of Regular gasoline should be less than or equal to 0.15 grams per litre
Now, we can set up the linear programming model for this problem and use software like Excel Solver or MATLAB to solve it and find the optimal values of the decision variables (H, J, S, R, HS, HR, JS, JR). The optimal solution will give us the minimum cost of producing Super and Regular gasoline while satisfying all the constraints.
mark me as brainliestLine r has an equation of y=
6/7x+1. Line s includes the point (7,–7) and is perpendicular to line r. What is the equation of line s?
Answers
The equation of line s is y + 7 = -7/6(x - 7).
What is slope of a line?
A line's steepness and direction are measured by the line's slope. A line's slope is determined by how its y coordinate changes in relation to how its x coordinate changes. y and x are the net changes in the y and x coordinates, Δy, Δx respectively. Consequently, it is possible to write the change in y coordinate with respect to the change in x coordinate as m = Δy/Δx
Given equation of line r is y = 6/7x+1.
The slope of line r is m = 6/7
The slope of the line that is perpendicular to line r is -1/m = - 7/6.
The equation of line that passes through the point (x₁, y₁) with slope m is y - y₁ = m(x - x₁).
Putting m = - 7/6, x₁ = 7 and y₁ = -7 in y - y₁ = m(x - x₁):
y - (-7) = - 7/6(x - 7)
y + 7 = - 7/6(x - 7)
To learn more about slope point form of a line, click on below link:
https://brainly.com/question/25312057
#SPJ1
10x + 8 = 3(x - 2)
10x + 8 = 3x
Answers
Answer:
1) -2
2) 8/7
Step-by-step explanation:
1) 10x+8=3(x-2)
10x+8=3x-6
10x-3x=-6-8
7x=-14
x=-2
2) 10x+8=3x
10x-3x=8
7x=8
x=8/7
Hope it helps
Edward works as a waiter, where his monthly tip income is normally distributed with a mean of $2,000 and a standard deviation of $350. Use this information to answer the following questions. Record yo
Answers
The probability that Edward’s monthly tip income exceeds $2,350 is 0.8413.
Given that Edward works as a waiter, where his monthly tip income is normally distributed with a mean of $2,000 and a standard deviation of $350.
The z score formula is given by;`z = (x - μ) / σ`
Where; x is the raw scoreμ the mean of the populationσ is the standard deviation of the population.
The probability that Edward’s monthly tip income exceeds $2,350 is to be found.`z = (x - μ) / σ``z = (2350 - 2000) / 350``z = 1`
The value of z is 1.
To find the area in the right tail, use the standard normal distribution table.
The table value for z = 1.0 is 0.8413.
Therefore, the probability that Edward’s monthly tip income exceeds $2,350 is 0.8413.
Know more about probability here:
https://brainly.com/question/251701
#SPJ11
I can’t really understand this can someone help
Me?
Answers
the probability that the interval estimation procedure will generate an interval that contains the actual value of the population parameter being estimated is the . a. error factor b. confidence coefficient c. confidence level d. level of significance
Answers
The answer is option b. confidence coefficient.
Why the confidence coefficient represents the probability?To explain this, let's start by defining interval estimation. Interval estimation is a statistical method used to estimate an unknown population parameter (such as the population mean or proportion) by constructing a range of values, called a confidence interval, that contains the true value of the parameter with a certain level of confidence.
The level of confidence refers to the percentage of times that the interval estimation procedure will generate an interval that contains the actual value of the population parameter being estimated. For example, a 95% confidence level means that if we were to repeat the interval estimation procedure many times, we can expect to obtain a confidence interval that contains the true population parameter 95% of the time.
The confidence coefficient, on the other hand, is the probability that a particular confidence interval actually contains the true value of the population parameter. It is the complement of the significance level, which is the probability of making a Type I error (rejecting a true null hypothesis). For example, if we have a 95% confidence level, then the confidence coefficient is 0.95, and the significance level is 0.05.
Therefore, the confidence coefficient represents the probability that the interval estimation procedure will generate an interval that contains the actual value of the population parameter being estimated. It is a measure of how confident we are that the estimated interval contains the true population parameter.
In conclusion, the confidence coefficient is a crucial concept in interval estimation that reflects the probability of obtaining a confidence interval that includes the true population parameter. It provides a measure of the reliability and accuracy of the interval estimation procedure and helps researchers interpret the results of their analyses.
Learn more about confidence coefficient
brainly.com/question/16984104
#SPJ11
For a Scalar function , Prove that X. ( =0)
(b) When X1 ,X2 ,X3 are
linearly independent solutions of X'=AX, prrove that
2X1-X2+3X3 is also a solution of
X'=AX
Answers
To prove that X(=0), we need to show that when X is a scalar function, its derivative with respect to time is zero.
Let's consider a scalar function X(t). The derivative of X(t) with respect to time is denoted as dX/dt. To prove that X(=0), we need to show that dX/dt = 0.
The derivative of a scalar function X(t) is computed as dX/dt = AX(t), where A is a constant matrix and X(t) is a vector function.
Since X(=0), the derivative becomes dX/dt = A(0) = 0. Thus, the derivative of X(t) is zero, which proves that X(=0).
Now, let's consider the second part of the question. We are given that X1, X2, and X3 are linearly independent solutions of the differential equation X'=AX. We need to prove that 2X1-X2+3X3 is also a solution of the same differential equation.
We can verify this by substituting 2X1-X2+3X3 into the differential equation and checking if it satisfies the equation.
Taking the derivative of 2X1-X2+3X3 with respect to time, we get:
d/dt (2X1-X2+3X3) = 2(dX1/dt) - (dX2/dt) + 3(dX3/dt)
Since X1, X2, and X3 are linearly independent solutions, we know that dX1/dt = AX1, dX2/dt = AX2, and dX3/dt = AX3.
Substituting these expressions, we get:
2(dX1/dt) - (dX2/dt) + 3(dX3/dt) = 2(AX1) - (AX2) + 3(AX3)
Using the properties of matrix multiplication, this simplifies to:
A(2X1-X2+3X3)
Thus, we can conclude that 2X1-X2+3X3 is also a solution of the differential equation X'=AX.
The proof shows that for a scalar function X(=0), the derivative is zero. Additionally, for the given linearly independent solutions X1, X2, and X3, the expression 2X1-X2+3X3 is also a solution of the differential equation X'=AX.
To know more about function visit:
https://brainly.com/question/11624077
#SPJ11
Read the word problem below.
Chan rows at a rate of eight miles per hour in still water. On Wednesday, it takes him three hours to row upstream from his house to the park. He rows back home, and it takes him two hours. What is the speed of the current?
Answers
Answer:
1 3/5 miles/hr
Step-by-step explanation:
Let C be the speed of the current
Let D be the distance between Chan's house and the park
We know that Distance, D, is = Speed x Time
-----
Chan's speed going upstream is (8 - C)mph.
That gives us:
D = (8-C)(3 hr)
Chan's speed going downstream is (8+C)mph
So we have:
D = (8+C)(2 hr)
We know that the d is the same for these two equations, so:
(8-C)(3 hr) = (8+C)(2 hr)
24 - 3C = 16 + 2C
5C = 8
C = (8/5) or 1 3/5 mph
Answer:
1.6 mph
Step-by-step explanation:
Distance, speed, and time are related by ...
distance = speed × time
We assume that the distances up and back are the same, so for a current speed of c, we have ...
3(8 -c) = 2(8 +c)
24 -3c = 16 +2c . . . eliminate parentheses
8 = 5c . . . . . . . . . . add 3c-16 to both sides
c = 8/5 = 1.6 . . . . . divide by 5
The speed of the current is 1.6 miles per hour.
A Farmer has 2400 feet of fencing and wants to fence off a rectangular field that boarders a straight river. He needs no fence along the river. What are the dimensions of the field that has the largest area
Answers
The dimensions of the rectangular field with the largest area are w = 600 feet and L = 1200 feet.
Let's denote the width of the rectangular field by w and its length by L.
Since the field borders a straight river, we only need to fence three sides of the rectangle, which gives us:
2w + L = 2400
Solving this equation for L, we get:
L = 2400 - 2w
Now, we want to find the dimensions of the field that will give us the largest possible area.
The area of a rectangle is given by A = wL. Substituting the expression for L from above, we get:
A = w(2400 - 2w)
= 2400w - 2\(w^2\)
To find the maximum value of this function, we can take its derivative with respect to w and set it equal to zero:
dA/dw = 2400 - 4w = 0
Solving for w, we get w = 600.
Substituting this value back into the equation for L, we get:
L = 2400 - 2w = 1200
For similar question on dimensions:
https://brainly.com/question/28688567
#SPJ11
So what are the chances of getting a 100% effort out of someone who never tries than someone who does??
Answers
Answer:
someone who doesn't try would have a lower chance of 100% effort and someone who dose try would have a much higher chance of 100% effort
Step-by-step explanation:
i hope this helps!!
Evaluate the expression.
4 (√147/3 +3)

Answers
Answer:
40
Step-by-step explanation:
4(sqrt(147/3)+3)
=4(sqrt(49)+3)
=4(7+3)
=4(10)
=40
select the statement that correctly describes a type i and a type ii error in this context.
a. Type I error occurs when the null hypothesis is accepted when it is actually true, while Type II error occurs when the null hypothesis is rejected when it is actually false.
b. Type I error occurs when the null hypothesis is rejected when it is actually true, while Type II error occurs when the null hypothesis is accepted when it is actually false.
c. Type I error occurs when the alternative hypothesis is accepted when it is actually true, while Type II error occurs when the alternative hypothesis is rejected when it is actually false.
d. Type I error occurs when the alternative hypothesis is rejected when it is actually true, while Type II error occurs when the alternative hypothesis is accepted when it is actually false.
Answers
The correct statement that describes Type I and Type II errors in hypothesis testing is:
b. Type I error occurs when the null hypothesis is rejected when it is actually true, while Type II error occurs when the null hypothesis is accepted when it is actually false.
In hypothesis testing, Type I error refers to rejecting the null hypothesis when it is actually true. This error represents a false positive result, indicating that a significant effect or relationship is detected when it does not exist in reality. Type II error, on the other hand, occurs when the null hypothesis is accepted (not rejected) when it is actually false. This error represents a false negative result, indicating a failure to detect a significant effect or relationship that does exist. The correct understanding and interpretation of Type I and Type II errors are crucial in hypothesis testing to ensure accurate conclusions.
Learn more about hypothesis testing here: brainly.com/question/29892401
#SPJ11
Reduce each of the following fractions to its simplest form. a. 12⁄18 b. 48⁄54 c. 27⁄90 d. 63⁄77 e. 24⁄32 f. 73⁄365
Answers
Answer: A. 2/3 B. 8/9 C. 3/10 D. 9/11 E. 3/4 F. 1/5
Step-by-step explanation:
divide -8x^4+5x^2-11x+4 by x-7
Answers
Divide
3
x
4
−
7
x
3
+
5
x
2
−
11
x
−
2
3
x
4
-
7
x
3
+
5
x
2
-
11
x
-
2
by
x
+
1
x
+
1
using long polynomial division.
3
x
3
−
10
x
2
+
15
x
−
26
+
24
x
+
1
On every Sunday in November, college football and men’s basketball teams are each ranked. During one weekend in November, the Oregon football team was ranked lower than the Oregon men’s basketball team. Later in the month, the football team was ranked higher than the basketball team, and yet there was no one week in which their rankings were equal. Why does this not violate the Intermediate Value Theorem?
Answers
The rankings are determined by different sets of criteria and can fluctuate from week to week based on the teams' performances. Therefore, the theorem does not apply in this situation.
The Intermediate Value Theorem states that if a function is continuous on a closed interval, it must take on every value between the function's endpoints at least once. In this case, we are not dealing with a function, but rather with rankings that are determined by subjective opinions and various factors such as wins, losses, and strength of schedule. While it may seem contradictory for the football team to be ranked lower than the basketball team at one point and then ranked higher later on without ever being ranked the same, it is not a violation of the Intermediate Value Theorem since the rankings are not continuous and do not follow a specific function.
Learn more about sets of criteria here
https://brainly.com/question/31647049
#SPJ11
Which expression is equivalent to [CHECK IMAGE BELOW], if x > 0?
![Which expression is equivalent to [CHECK IMAGE BELOW], if x > 0?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/LGYxxIdIfdPFKYPHOUw3cbDkjnzQdNdb.png)
Answers
Answer:
C. 4x²√(3x)
Step-by-step explanation:
You want to simplify √(48x⁵).
Simplifying RadicalsSquare root expressions can be simplified by removing perfect squares from under the radical:
\(\sqrt{48x^5}=\sqrt{16x^4\cdot3x}=\sqrt{(4x^2)^2}\cdot\sqrt{3x}=\boxed{4x^2\sqrt{3x}}\)
8^17/8 in simplified answer
NO LINKS THEY DONT WORK?THEY ARE BLOCKED
Answers
Answer:
its 8^16
Step-by-step explanation:
let 8=8^1
when dividing exponents, you subtract the exponents
8^17/8=8^(17-1)=8^16
Hope this helps
What attributes do squares and
trapezoids always have in
common?
Answers
Answer:
There both quadrilaterals
Step-by-step explanation:
Your friend has $100 when he goes to the fair. He spends $10 to enter the fair and $20 on food.
Rides at the fair cost $2.00 per ride.
The function f(x) = -2x + 70 can be used to determine how much money he has left over after x
rides? What does f(17) represent?
O Your friend paid for 17 rides and had $36 left over.
O Your friend paid for 17 rides and had $64 left over.
O Your friend paid for 17 rides and spent $36.
O Your friend paid for 17 rides and spent $64
Answers
The answer is A f(x)=-2x + 70
The $100 budget, $10 entrance fee, as well as the $20 spent on food are considered to be constants with the budget being a positive and the money spent on the entrance and food as negatives. This provides you with a positive 70. The variable x here is the number of rides your friend might take and the -2 multiplied to it is the money to be spent per ride.
Example:
When your friend has ridden a total of 5 rides, x = 5 therefore
-2(5) + 70 = 60
Your friend upon going on 5 rides would have $60 left.
a random sample of 1000 people was taken. four hundred fifty of the people in the sample favored candidate a. what is the upper limit for a 95% confidence interval for the true proportion of people who favored candidate a? round your answer to three decimal places.
Answers
The 95% confidence interval for the true proportion of people who favored candidate a is 0.419, 0.481
How to calculate confidence interval?
First, calculate sample proportion by divide number people who favored candidate by number of sample. So:
\(\pi\) = 450 / 1,000 = 0.45
Then we use the formula for confidence interval
\(\pi\) ± \(z\sqrt{\frac{\pi (1-\pi )}{n}}\)
In which z is z score that has a p value of \(1 - \frac{\alpha }{2}\)
For 95% confidence interval z is the value of Z that has a p value of \(1 - \frac{0.05}{2}\) = 0.975, so z = 1.96
After we have \(\pi\) value and z value then put it in the formula. So:
= 0.45 ± \(1.96\sqrt{\frac{0.45(1-0.45)}{1000} }\)
= 0.45 ± 0.0308
= 0.419, 0.481
Thus, the 95% confidence interval for the true proportion of people who favored candidate a is 0.419, 0.481
Learn more about confidence interval here:
brainly.com/question/24131141
#SPJ4
repper took her kids to ride the Ferris wheel in Niagara Falls. Their height over time can be modelled by a sinusoidal function. They reached a maximum height of 62 m at 15 min, and a minimum height of 6 m at 25 min. 1. Submit your FUIL Solutions to the "Assignment" link for Culminating 2. Enter the answer for part g) below. a) What is the equation of the axis of the function, and what does it represent in this situation? b) What is the amplitude of the function, and what does it represent in this ituation? c) What is the period of the function, and what does it represent in this situation? d) Determine the k-value that would be used in the equation. e) If a single ride is 4 rotations of the Ferris wheel, state the domain and range, starting at t=0. f) Write a sinusoidal function to model their height relative to time. g) Use your equation to determine a rider's height after one hour. Question 6 ( 1 point) Enter the rider's height after one hour to 2 decimal places below.
Answers
The equation of the Ferris wheel's sinusoidal function is h(t) = 28 * sin(π/5 * (t - 15)) + 34. Using this equation, you can determine the rider's height after one hour by substituting t = 60 into the equation.
a) The equation of the axis of the function is the average of the maximum and minimum heights. In this situation, the average is (62 + 6) / 2 = 34 m. The axis represents the average or midpoint height of the Ferris wheel ride.
b) The amplitude of the function is half the difference between the maximum and minimum heights. In this case, the amplitude is (62 - 6) / 2 = 28 m. The amplitude represents the maximum deviation from the axis, which is the distance from the average height to the maximum or minimum height.
c) The period of the function is the time it takes for one complete cycle of the sinusoidal function. In this situation, the period is the time difference between two consecutive maximum or minimum heights, which is 25 min - 15 min = 10 min. The period represents the duration of one complete up-and-down cycle of the Ferris wheel.
d) The k-value in the equation represents the angular frequency, which is related to the period of the function. The angular frequency is given by k = 2π / period. So in this case, k = 2π / 10 = π / 5.
e) Since a single ride is 4 rotations of the Ferris wheel, the domain starts at t = 0 and ends at t = 4 times the period. Therefore, the domain is [0, 4(10)] = [0, 40] minutes. The range is the minimum and maximum heights, which are [6, 62] meters.
f) The sinusoidal function to model their height relative to time can be written as h(t) = A * sin(k(t - c)) + d, where A is the amplitude, k is the angular frequency, c is the horizontal shift, and d is the vertical shift. Plugging in the given values, we have h(t) = 28 * sin(π/5 * (t - 15)) + 34.
g) To determine the rider's height after one hour (60 minutes), we substitute t = 60 into the equation: h(60) = 28 * sin(π/5 * (60 - 15)) + 34. Calculating this value gives the rider's height after one hour.
Learn more about sinusoidal function here:
https://brainly.com/question/13945310
#SPJ11