Identify the terms, like terms, coefficients, and constants in each expression.

1. 2 + 3a + 9a

2. 7 - 5x + 1

Answer: 28.3 yards

Step-by-step explanation:

Answer:

19 and 27

Step-by-step explanation:

let 'x' = larger number

let 'x-8' = smaller number

x + (x-8) = 46

2x - 8 = 46

2x = 54

x = 27

x-8 = 19

Answer:

C

Step-by-step explanation:

(x-3)+7

Answer:

A

Step-by-step explanation:

b would +3 which is not right

c is also right...

d would be -x which is not right

The expression contain sum and factor.

The correct option is (C).

Mathematical statements are called expressions if they have at least two terms that are related by an operator and contain either numbers, variables, or both. Addition, subtraction, multiplication, and division are all possible mathematical operations.

Given:

3 x(5+7)

In the Above Expression we have two operation Multiplication and Addition.

Also, the Multiplication is also termed as factor.

Hence, the expression contain sum and factor.

Learn more about Expression here:

https://brainly.com/question/14083225

#SPJ2

The reflexive closure of a relation on a set is the smallest reflexive relation that contains the original relation. In other words, it is the addition of pairs that ensure every element in the set is related to itself. To form the reflexive closure, we need to add pairs that relate each element in the set to itself.

To form the reflexive closure of relation r on the set {0, 1, 2, 3}, we need to add ordered pairs that ensure every element in the set is related to itself. In other words, we need to add pairs of the form (x, x) for each element x in the set that is not already present in relation r.

In this case, the reflexive closure of relation r would require adding the following ordered pairs: (0, 0), (1, 1), (2, 2), and (3, 3). These pairs ensure that every element in the set {0, 1, 2, 3} is related to itself, making the relation reflexive. These pairs ensure that every element is related to itself, satisfying the reflexivity property.

By adding these additional ordered pairs, we have modified relation r to include reflexivity, as every element now has a direct relation to itself in the set.

To know more about reflexive closure, refer here :

https://brainly.com/question/30105348#

#SPJ11

Answer:

  λ = 3

Step-by-step explanation:

You want the value of λ that places point C = λ(i -3j) on the line between A(-5i -11j) and B(23i -4j).

The parameterized line between A and B is ...

  P = A +t(B -A)

where P is a point on AB. We can set P = C to find the value of t that identifies the point on AB. Comparing that to C, we can determine the value of λ.

  λ(i -3j) = -5i -11j +t(23i -4j -(-5i -11j)) = (-5+28t)i +(-11 +7t)j

Equating components gives two equations in the unknowns λ and t:

Multiplying the second equation by -4 and adding the first gives ...

  -4(-3λ) +λ = -4(-11 +7t) +(-5 +28t)

  13λ = 39 . . . . . . . simplify

  λ = 3 . . . . . . . . . divide by 13

Answer:

What is G

Step-by-step explanation:

6-3=3g

6+3=9g

=0

Answer:

Step-by-step explanation:

Triangle DEF is triangle ABC rotated by 180°

So:

∠A is corresponding to ∠D

∠B is corresponding to ∠B

and ∠C is corresponding to ∠F

based on the principle of mathematical induction, we conclude that \(2^{n}\) > \(n^{2}\) for all n greater than 4.

By using mathematical induction, we can prove that \(2^{n}\) > \(n^{2}\) for all n greater than 4.

Base case (n = 5):

When n = 5, we have \(2^{5}\) = 32 and \(5^{2}\) = 25. Since 32 is indeed greater than 25, the inequality holds for n = 5.

Inductive step:

Assuming the inequality holds for some positive integer k: \(2^{k}\) > \(k^{2}\), we need to show that it also holds for k + 1: \(2^{(k+1) }\) > \((k+1)^{2}\)

Starting with the left-hand side:

\(2^{(k+1) }\) = 2 × \(2^{k}\)

Using the inductive assumption, we can rewrite it as:

\(2^{(k+1) }\) > 2 ×\(k^{2}\)

Now let's consider the right-hand side:

\((k+1)^{2}\) = \(k^{2}\) + 2k + 1

We want to show that 2 × \(k^{2}\) > \(k^{2}\) + 2k + 1.

Simplifying the inequality, we have:

\(k^{2}\) - 2k - 1 > 0

By analyzing the quadratic function f(k) = \(k^{2}\) - 2k - 1, we find that it is positive for all k greater than 4.

learn more about mathematical induction here:

https://brainly.com/question/29503103

#SPJ11

Answer:

Step-by-step explanation:

Let's start by using the trigonometric identity for the sum of two cosines:

cos(a) + cos(b) = 2 cos((a+b)/2) cos((a-b)/2)

We can apply this identity to the first two terms:

cos(pi/7) + cos(3pi/7) = 2 cos((pi/7 + 3pi/7)/2) cos((3pi/7 - pi/7)/2)

Simplifying the angles in the equation above:

cos(pi/7) + cos(3pi/7) = 2 cos(2pi/7) cos(pi/7/2)

Now we can apply the identity again to the second and third terms:

cos(3pi/7) + cos(5pi/7) = 2 cos((3pi/7 + 5pi/7)/2) cos((5pi/7 - 3pi/7)/2)

Simplifying the angles again:

cos(3pi/7) + cos(5pi/7) = 2 cos(4pi/7) cos(pi/7/2)

Notice that cos(4pi/7) is the same as cos(3pi/7 + pi/7) and we can use the identity again:

cos(4pi/7) = cos(3pi/7 + pi/7) = cos(3pi/7) cos(pi/7) - sin(3pi/7) sin(pi/7)

Substituting the expression for cos(4pi/7) and adding the two previous equations:

cos(pi/7) + cos(3pi/7) + cos(5pi/7) = 2 cos(pi/7/2) [ cos(2pi/7) + cos(3pi/7) cos(pi/7) - sin(3pi/7) sin(pi/7) ]

Now we can use the identity cos(2a) = cos^2(a) - sin^2(a) to simplify the expression inside the brackets:

cos(pi/7) + cos(3pi/7) + cos(5pi/7) = 2 cos(pi/7/2) [ cos(3pi/7) cos(pi/7) - sin(3pi/7) sin(pi/7) + cos^2(3pi/7) - sin^2(3pi/7) ]

The terms in the brackets can be simplified using the identity cos(pi/7) = cos(6pi/7) and sin(pi/7) = sin(6pi/7):

cos(pi/7) + cos(3pi/7) + cos(5pi/7) = 2 cos(pi/7/2) [ cos(3pi/7) cos(6pi/7) - sin(3pi/7) sin(6pi/7) + cos^2(3pi/7) - sin^2(3pi/7) ]

cos(pi/7) + cos(3pi/7) + cos(5pi/7) = 2 cos(pi/7/2) [ cos(3pi/7 - 6pi/7) + cos^2(3pi/7) - sin^2(3pi/7) ]

cos(pi/7) + cos(3pi/7) + cos(5pi/7) = 2 cos(pi/7/2) [ -cos(3pi/7) + cos^2(3pi/7) - sin^2(3pi/7) ]

Now we can use the identity cos^2(a)

Answer: 3.15

Step-by-step explanation:

In total, Menaha traveled 97km 1000m (97.1km).

Distance is a numerical measurement of how far apart two objects, points, or places are in space. Distance can be measured in linear units such as meters, kilometers, feet, miles, etc. It can also be measured in angular units such as degrees or radians.

Distance can also refer to the space between two points in time, such as the time between two events. Distance can be used to measure physical distance, time, or even emotional distance.
To calculate this, the two distances must be added together.
The train distance is =86km 520m (86.52km)

and the car distance is =11km 480m (11.48km).
When added together, =86km 520m+11km 480m = 97.52km.
However, since the distances are measured in km and m,
it is necessary to convert the measurements into a single unit of measurement.
To do this, the measurements must be converted into metres.
The train distance is 86,520 metres

And the car distance is 11,480 metres.
When added together,

the total distance is 97,000 metres (97km).

To know more about distance click-
https://brainly.com/question/23848540
#SPJ4

Answer:

Converse of the Alternate Exterior Angles Theorem.

Step-by-step explanation:

The alternate exterior angles theorem explains that "if a pair of parallel lines are cut by a transversal, then the alternate exterior angles are congruent." Judging from the fact that the problem is including <1 and <8, we can safely assume that it is including this theorem since both of said angles are on the exteriors of the pair of parallel lines. Not to mention that this principle also effectively proves that both lines are parallel to each other, thus proving this sentence true.

Answer:

Hope it helps dear.Please let me know

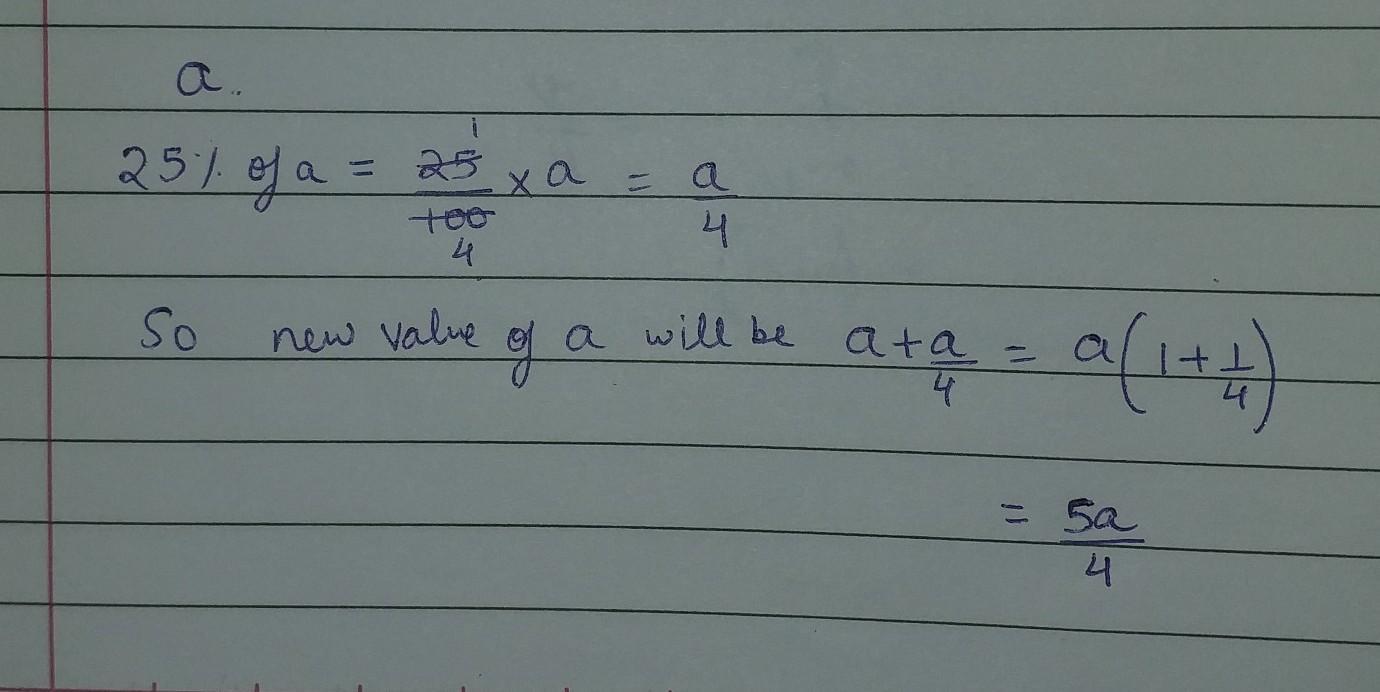
a increased by 25% means multiply the number with 1.25

For example, let the number be m,

1 * m = m ....which is the 100%, original

1.25 * m = 1.25m .....which is 125%, 25% increased

Answer:

See below

Step-by-step explanation:

g (h(6))   :

   h (6) =  3 ( 6^2) + 2 = 110

   then g (110) =   sqrt (110)

h (g(5))

    g(5) = sqrt 5

        then h( sqrt5) = 3 ( sqrt5)^2 + 2 = 17

The smallest value of n needed so that the probability that the system functions is at least 0.90 is 12. Probability is a measure of the likelihood of an event occurring. In a mathematical sense, probability is a value between 0 and 1 that represents the chance of a particular event happening.

In a 3 out of n system, the probability that the system functions is given by the formula:

P(function) = \(1 - (1 - p)^3 * (1 - (1 - p)^(^n^ - ^3^))\)

where p is the probability that each component functions (in this case, 0.9) and n is the total number of components.

To find the smallest value of n that satisfies the condition P(function) ≥ 0.9, we can rearrange the formula to:

n ≥ 3 + log(1 - 0.9) / log(1 - 0.9)

By solving this equation, we find that the smallest value of n that satisfies the condition is n ≥ 12.

Learn more about probability, here https://brainly.com/question/30034780

#SPJ4

Answer:

13

Step-by-step explanation:

Use the distance formula to solve for the distance between two points.

\(d=\sqrt{(x2-x1)^2 + (y2-y1)^2\)

Plug in your coordinate points.

\(d=\sqrt{(7-(-5))^2 + (2-7)^2\)

\(d=\sqrt{(12)^2 + (-5)^2\)

\(d=\sqrt{144 + 25\)

\(d=\sqrt{169\)

d= 13

Answer: look it up frfr

Step-by-step explanation:

The forecast for May using a five-month moving average is 39 (Option E).

Moving average is used for smoothing out time series data to find any trends or cycles within the data. A five-month moving average is the average of the past five months. To calculate the moving average, add up the sales for the previous five months and divide it by five.

According to the question, the sales for the previous five months are: Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47

We have to add the sales of these five months, which gives:

27 + 40 + 42 + 41 + 47 = 197

To find the moving average for May, we divide this sum by 5:

197 / 5 = 39.4

Since we have to round the answer to the nearest whole number, we round 39.4 to 39, which is option E.

Learn more about Moving average here: https://brainly.com/question/28495879

#SPJ11

Answer: Converges to 0

Step-by-step explanation:

took test

Answer:

its not b

Step-by-step explanation:

Answer:

112 degree=x.

hope it would help

Answer:

8, 0

Step-by-step explanation:

Answer:
A part to part ratio is the porportion if the diff parts in relation to each other

Step-by-step explanation:

The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).

To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.

The population proportion who participated in voting is given as 63% of all registered voters.

This means that out of every 100 registered voters, 63 participated in voting.

In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.

Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .

Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).

Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.

It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.

For similar question on population proportion.

https://brainly.com/question/29516589  

#SPJ8

Answer:

168

Step-by-step explanation:

In the US, housing prices and consumption generally change in the same direction.

Changes in housing prices can have an impact on consumption patterns in the US. Generally, when housing prices increase, consumption also tends to increase, and when housing prices decrease, consumption tends to decrease as well. This relationship can be attributed to several factors. Firstly, when housing prices rise, homeowners experience an increase in their wealth through home equity.

This increase in wealth can lead to higher consumer confidence and a willingness to spend more on goods and services, thereby boosting consumption. Secondly, rising housing prices can also lead to a "wealth effect" for homeowners. This means that homeowners may feel wealthier and more financially secure, leading them to increase their discretionary spending and overall consumption. Conversely, when housing prices decline, homeowners may experience a decrease in their wealth and financial security.

Learn more about prices here:

https://brainly.com/question/19091385

#SPJ11

The solution to the given differential equation is y = e⁽ˣ³⁾⁽²⁸ˣ ⁺ ᶜ⁾, where C is a constant.

To solve the first-order linear differential equation of the form y' + p(x)y = q(x), where p(x) and q(x) are functions of x:

Find the integrating factor (IF) = e⁽∫ᵖ⁽ˣ⁾ᵈˣ⁾

Multiply both sides of the equation by the IF.

Apply the product rule to the left side and simplify the right side.

Integrate both sides with respect to x.

Solve for y.

Using this method, for the given equation:

y' - 3x²y = 28e⁽ˣ³⁾

Find the integrating factor (IF):

IF = e⁽∫ᵖ⁽ˣ⁾ᵈˣ⁾ = e⁽⁻³/¹ * ∫ˣ²ᵈˣ⁾ = e⁽⁻ˣ³⁾

Multiply both sides by the IF:

e⁽⁻ˣ³⁾y' - 3x²e⁽⁻ˣ³⁾y = 28

Apply the product rule to the left side and simplify the right side:

d/dx (e⁽⁻ˣ³⁾y) = 28

Integrate both sides with respect to x:

e⁽⁻ˣ³⁾)y = 28x + C, where C is the constant of integration.

Solve for y:

y = e⁽ˣ³⁾(28x + C)

Therefore, the solution to the given differential equation is y = e⁽ˣ³⁾(28x + C), where C is a constant.

Learn more about linear equation here: brainly.com/question/12423682

#SPJ4

Complete question:

How to solve the first order linear differential equation

Y'- 3x²y=28eˣ³

Answer:

​Adjacent: ​∠CEA and ​∠AED

Complementary: none

Supplemntary: ​∠CEA and ​∠AED

Veritcal: ​∠CEA and ​∠DEB

Step-by-step explanation:

Answer:

​Adjacent: ​angles CEA and ​AED

Vertically opposite: angles ​CEA and DEB

Complementary: none

Supplementary: angles ​CEA and ​AED

Hope this helps!

Answer: 88 1/2

Step-by-step explanation:

easy

Answer:

89

Step-by-step explanation: