Identitfy a fraction between 1/3 and 5/6
Answers
Answer:
3/6, 4/6, 1/2, or 2/3
Step-by-step explanation:
turn 1/3 into 2/6(equivalent fraction)
find a fraction inbetween 2/6 and 5/6
this can be 3/6 or 4/6. these can also be simplified down to 1/2 or 2/3
Answer:
3/6
Step-by-step explanation:
1/3 = 1x2 / 3x2 = 2/6 [Equivalent Fraction]
A fraction between 2/6 and 5/6 is,
=> 3/6
Related Questions
_ divided by 4= _ remaider 5
Answers
Answer:
20 / 4 =5
Step-by-step explanation:
I think
A certain forest covers an area of 3700 km^2. suppose that each year this area deacreases by 8.75%. What will the are be after 13 years. Round to the nearest square kilometer.
Answers
Answer: The area of the forest after 13 years will be approximately 1457 km^2.
Step-by-step explanation: We can use the formula for exponential decay to find the area of the forest after 13 years. The formula is:
A = A0 * (1 - r)^t
where A is the final area, A0 is the initial area, r is the rate of decay as a decimal, and t is the time in years.
For this problem, A0 = 3700 km^2, r = 0.0875 (8.75% as a decimal), and t = 13 years. Plugging in these values, we get:
A = 3700 * (1 - 0.0875)^13
A = 3700 * 0.5323
A = 1968.51 km^2
Rounding to the nearest square kilometer, the area of the forest after 13 years is approximately 1457 km^2.
Hope this helps, and have a great day!
In this 30°-60°-90° right triangle, the length of the long leg is 9√3
What is the measure of the hypotenuse n and the short leg m?
30°
9√3
n
m
Answers
Answer:
30°
Step-by-step explanation:
Answer:
9
Step-by-step explanation:
In a 30°-60°-90° right triangle, the sides are always in the ratio of 1: √3:2, where 1 is the length of the short leg opposite the 30° angle, √3 is the length of the long leg opposite the 60° angle, and 2 is the length of the hypotenuse opposite the 90° angle1234.
In this case, we are given that the long leg is 9√3, so we can use this value to find the other sides by setting up a proportion:
short leglong leg=13
short leg93=13
Cross-multiplying and solving for the short leg, we get:
short leg=393×1=9
Similarly, we can use another proportion to find the hypotenuse:
long leghypotenuse=32
93hypotenuse=32
Cross-multiplying and solving for the hypotenuse, we get:
hypotenuse=32×93=18
Therefore, the measure of the hypotenuse n is 18 and the measure of the short leg m is 9.
PLEASE I REALLY NEED THIS HELP
solve the triangle. round to the nearest tenth

Answers
The correct solution of the triangle is seen in option D
How do you solve the triangle?In this case, we would need to use the sine rule so as to solve the triangle as we have in the problem that is before us here. The sine rule states that;
a/Sin A = b/SinB = c/SinC
We know that we can be able to obtain the angle C using the sine rule;
29/Sin 42 = 33/SinC
SinC = 33Sin42/29
C = Sin-1(33Sin42/29)
C = 49.6 degrees
The angle B is now;
180 - (42 + 50)
B = 88.4 degrees
Then;
b/Sin 88 = 29/Sin42
b = 29 Sin 88/Sin42
b = 28.98/0.669
b = 43.3
Learn more about triangle:https://brainly.com/question/2773823
#SPJ1
His wife makes a final test of Odysseus' identity by getting him to tell
about the building of his bed
the name or his favorite dog
about the day he went away
how he got a scar on his arm
Answers
Answer: About the building of his bed
He built the bed around an olive tree that was growing where the bedroom was situated, and he even incorporated the tree into the bed; therefore moving the bed is an impossible feat.
11. m2 = 340 Find m 24 and explain how you know. (2 points)
1
X
3
Drawing not to scale.

Answers
Answer:
Angle 4 also has a measurement of 34 degrees because opposite angles of intersecting lines are congruent. In other words, angles 2 and 4 are congruent, so are angles 1 and 3.
Factor Problem Completely 16n^3 - 56n^2 + 8n - 28

Answers
Given
The equation is given as
\(16n^3-56n^2+8n-28\)Explanation
Factorisation the equation,
\(4(4n^3-14n^2+2n-7)\)Factorise the polynomial.
\(4(2n-7)(2n^2+1)\)AnswerHence the answer is
\(4(2n-7)(2n^2+1)\)which expression is equivalent to (x+3)^3-9x(x+3)?
a. X^3-9x^2+27x+27
b. x^3-9x^2-27x+27
c. x^3+27
d. x^3-27
Answers
Whats 2+2+2+2+7+9+17+98+76+918÷5
Answers
Answer:
398.6
Step-by-step explanation:
Any calculator will work.
solve this problem

Answers
Answer:
a+b=3
and
a–b=3
I Think it help you
What is the total amount of outcomes possible when a coin is tossed four times and a card if selected from a standard deck of cards.
Answers
Answer:
About 60 pecent
Step-by-step explanation:
Answer: 832 possible outcomes
To find the total number of outcomes when a coin is tossed four times and a card is selected from a standard deck of cards, we need to multiply the number of outcomes for each event.
The number of outcomes for a coin toss is 2 (heads or tails), and we toss the coin 4 times. Therefore, the number of outcomes for the coin tosses is:
2 x 2 x 2 x 2 = 16
The number of outcomes when selecting a card from a standard deck of cards is 52. Therefore, the total number of outcomes when a coin is tossed four times and a card is selected from a standard deck of cards is:
16 x 52 = 832
So there are 832 possible outcomes when a coin is tossed four times and a card is selected from a standard deck of cards.
Which expression is a perfect cube?

Answers
A lot of points. PLEASE HELP! I will mark brainliest. Whoever gets it right first.

Answers
- the last one is your answer, you can use the small lines on the side of triangle to help you know which ones match with each other
Determine the relative maxima of f(x)=2x^3-3x^2. Also describe where the function os increasing and decreasing.
Answers
Answer:
Below in bold.
Step-by-step explanation:
f(x)=2x^3-3x^2
Finding the derivative and equating to zero:
f'(x) = 6x^2 - 6x = 0
6x(x - 1) = 0
So there are turning point at x = 0 and 2 = 1.
Finding the relative maximum:
Second derivative is negative when we have a maximum value:
f"(x) = 12x - 5
- which is negative when x = 0.
So the relative maximum is at x = 0 where f(x) = 2(0)^3 - 3(0)^2 = 0.
At x = 1, second derivative = 12(1) - 5 = +7 so this is a relative minimum.
The function is increasing in interval -∝ < x < 0
decreasing in interval 0 < x < 1
then increasing in interval 1 < x < ∝
How to solve ?? 3 (3z-6)=0
Answers
Answer:
Step-by-step explanation:
3(3z-6)=0
multiply your three with the 3z and the -6
9z-18=0
figure out what - 18 = 0
9z=18
9*2=18
z=2
hope this helps
You rent an apartment that costs $1100 per month during the first year, but the rent is set to go up $110 per year. What would be the monthly rent during the 11th year of living in the apartment?
Pls answer
Answers
Answer: The initial cost on rent on your first year living there is 1100. Supposing you live there for another 11 years your rent would be 2200 per month.
Step-by-step explanation:110x11=1100 1100+1100=2200
Answer: I think it's 1,100
Step-by-step explanation: We know that the apartment costs $1100 per month during the first year but if it goes up 110 dollars per year how much would total be in 11th year?
First we need to multiply 1100 and 110 which equals 121,000
Secondly, of course we need to make sure that our anwser is correct, now we divide 121,000 with 11 years (which equals 1100)
But of course if it is not correct, I'm very sorry. But Have a nice day/night!
Hope it helped!
-GreenteaStudys
What is the value of 2 for the following data to three decimal places?OA. 0.867X34LO57y245610 20

Answers
Explanation
We are given the data below:
We are required to determine the value of r² using the table above.
This is achieved thus:
- Using a graphing calculator, we have:
- From the graph above, we have:
\(r^2=0.8674\)Hence, the answer is:
\(r^2\approx0.867\)Option A is correct.


I need the answer asap

Answers
Write and solve an equation to find the value of x and the missing angle measures

Answers
Answer:
in explanation
Step-by-step explanation:
angle rules say that those angles respond to each other meaning
they will equal each other
so 6x-4=4x+14
now solve for x
x=9
the top angle will be
6(9)-4=50
bottom angle will be 50
4(9)+14=50
Find x (circle)
(Btw I don’t know if 5.6 is correct so just ignore that)

Answers
Answer:
A. 11.2
Step-by-step explanation:
But this has nothing to do with 5.6 × 2. Erase that! Lol.
You have a right triangle here. The only thing to do with the circle is that there are two radii (plural of radius) shown. So they have to be the same measure.
The unmarked "bottom" of the triangle, the short leg, is a radius, so it too, is 8.4.
The hypotenuse of the right triangle, the side on the right, the longest side is 5.6 + 8.4.
The hypotenuse is 14.
Let's do some Pythagorean Theorem.
Leg^2+ leg^2=hypotenuse^2
you know,
a^2 + b^2 = c^2
fill in what we know.
8.4^2 + b^2 = 14^2
simplify.
70.56 + b^2 = 196
subtract 70.56
b^2 = 125.44
squareroot both sides
b = 11.2
given the system of linear equations, written in column form as follows which of the following is the corresponding row form of this system?
Answers
The row form of the system is 5x = 2 and y – y = 0.
Column form:
3x + y = 5
2x – y = –3
Row form:
3x + 2x = 5 – 3
y – y = 0
The row form of this system is 3x + 2x = 5 – 3 and y – y = 0. To convert from column form to row form, the first step is to eliminate the y terms in the equations. To do this, we need to add the two equations together. This gives us:
3x + y = 5
2x – y = –3
3x + 2x = 5 + (–3)
y – y = 0
5x = 2
y – y = 0
Finally, we can solve for x and y.
5x = 2 ⇒ x = 2/5
y – y = 0 ⇒ y = 0
Therefore, the row form of the system is 5x = 2 and y – y = 0.
Learn more about system of linear equations here:
https://brainly.com/question/19549073
#SPJ4
Researchers asked 250 families whether or not they were homeowners and how many cars they had. Their responses are summarized in the following table.
No car or one car Two or more cars
Homeowner
25
90
Not a homeowner
45
90
(a) what percentage of the families are homeowners?
(b) What percentage of the familles have two or more cars?
х
S
?
(b) 1%
Explanation
Check
2021 McGraw-Hill Education. All Rights Reserved. Terms of Use Privacy. Accessibility

Answers
Answer:
A = 46%
B = 72%
Step-by-step explanation:
Hello I need help on this question:Which of the following inequalities matches the graph?
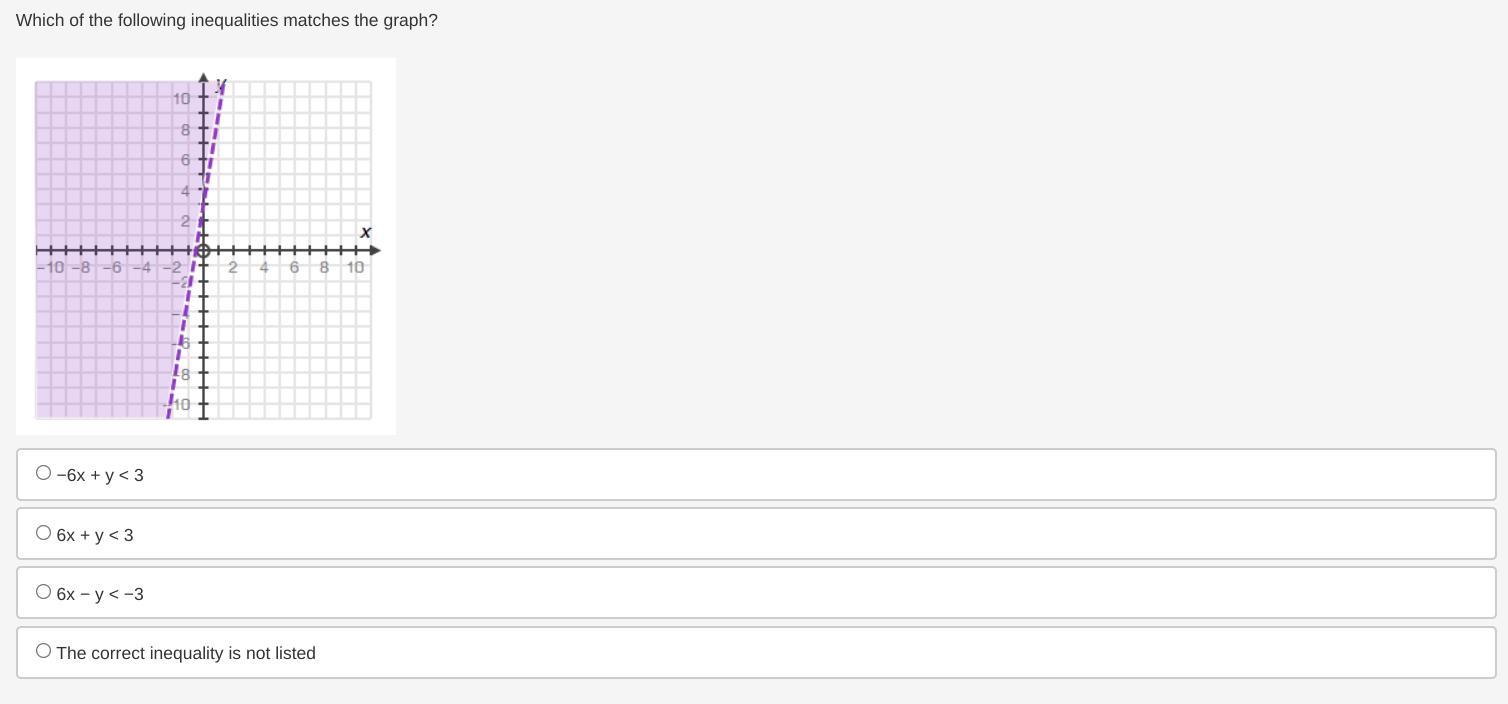
Answers
Among the options of inequalities given, the inequality in 3rd option, \(6x-y < -3\) matches the graph.
From the given graph, it can be determined that -
The function is increasing. This implies the function has a positive slopeThere is a shaded region to the left of the dashed line representing the function. This implies the inequality for the function can be represented as a ">" sign after the "y" termFrom the above information, the inequality can be represented in a general term as -
\(y > ax+b\) where, a>0 ---- (1)
For the given option (a), it is given that -
\(-6x+y < 3\)
This can also be written as -
\(-6x+y < 3\\= y < 6x+3\) ----- (2)
It can be seen that the equation (2) is not in the form of equation (1). So, option (a) is not the correct inequality.
Now, considering the given option (b), it is given that -
\(6x+y < 3\)
This can also be written as -
\(6x+y < 3\\=y < 3-6x\) ------ (3)
It can be seen that the equation (3) is not in the form of equation (1). So, option (b) is not the correct inequality.
Now, let us consider the given option (c). It is given that -
\(6x-y < -3\)
This can also be written as -
\(6x-y < -3\\=-y < -3-6x\\=y > 6x+3\)--------- (4)
It can be seen that the equation (4) is in the form of equation (1). So, option (c) is the correct inequality.
Thus, it can be said that the inequality in option (c), \(6x-y < -3\) matches the graph.
To learn more about inequality visit https://brainly.com/question/28823603
#SPJ9
If 15% of the customers total is $98,880, then the sum total equals what
Answers
The sum total by the given data is equals to $658,880.
We are given that;
Percent=15%
Amount= $98,880
Suppose the value of which a thing is expressed in percentage is "a'
Suppose the percent that considered thing is of "a" is b%
Then since percent shows per 100 (since cent means 100), thus we will first divide the whole part in 100 parts and then we multiply it with b so that we collect b items per 100 items(that is exactly what b per cent means).
To divide by a percentage, we can convert it to a decimal by moving the decimal point two places to the left. This gives us:
15% = 0.15
To divide by 0.15, we can multiply by its reciprocal, which is 1/0.15. This gives us:
$98,880 / 0.15 = $98,880 x 1/0.15
To multiply by 100, we can move the decimal point two places to the right. This gives us:
$98,880 x 1/0.15 x 100 = $658,880
Therefore, by the percentage the answer will be $658,880.
Learn more about percent here:
https://brainly.com/question/11549320
#SPJ1
Approximate the area of the circle segment bounded by DE and arc DE if r =20 and theta=47°. Photo Attached

Answers
Answer: 1256.63706
Step-by-step explanation: A=(π20)2
The approximate area of the circle segment bounded by arc DE and chord DE is approximately 17.72 square units.
To approximate the area of the circle segment bounded by arc DE and chord DE, you can use the following formula:
Area = (1/2) * r^2 * (θ - sinθ)
Where:
r is the radius of the circle (r = 20 in your case).
θ is the central angle in radians (47° converted to radians is approximately 0.8203 radians).
Let's calculate it:
θ = 47° * (π / 180) ≈ 0.8203 radians
Now, plug these values into the formula:
Area = (1/2) * (20^2) * (0.8203 - sin(0.8203))
Area ≈ (1/2) * 400 * (0.8203 - 0.7317)
Area ≈ (1/2) * 400 * 0.0886
Area ≈ 17.72 square units
for such more question on circle segment
https://brainly.com/question/10645610
#SPJ2
Help this is worth 20 points!!

Answers
(x−6)(2x−7) plz help
Answers
Answer:
38 bb 2
Step-by-step explanation:
slimeeyyy
Answer:
2x^2 + 19x +42
Step-by-step explanation:
x . 2x = 2x^2
x . 7 = 7x
6 . 2x = 12x
6 . 7 = 42
7x + 12x = 19x
2x^2 + 19x +42
if a coin is flipped 35 times and lands on heads 21 times what is the relative frequency of Landing on heads
Answers
Work Shown:
21/35 = (7*3)/(7*5) = 3/5
Find the unit price for both quantities: 5 gallons of enamel paint for $62.00 and 8 gallons for $83.00
Answers
Answer:
Unit 1= $12.4 per gallon
Unit 2= $10.375 per gallon
Step-by-step explanation:
Given
\(Quantity\ 1= 5\ gallons\)
\(Price = \$62.00\)
\(Quantity\ 2= 8\ gallons\)
\(Price =\$83.00\)
Required
The unit price
The unit price is calculated as:
\(Unit = \frac{Price}{Quantity}\)
So, we have:
\(Unit\ 1= \frac{Price \ 1}{Quantity\ 1}\)
\(Unit\ 1= \frac{\$62.00}{5\ gallons}\)
Unit 1= $12.4 per gallon
\(Unit\ 2= \frac{Price \ 2}{Quantity\ 2}\)
\(Unit\ 2= \frac{\$83.00}{8}\)
Unit 2= $10.375 per gallon
) In a geometric progression, the sum of the first two terms is equal to 16. The sum to infinity is equal to 25. Find the possible values of the first term.
Answers
There are no possible real values for the first term 'a' that satisfy both equations.
Let's denote the first term of the geometric progression as 'a' and the common ratio as 'r'.
The sum of the first two terms can be expressed as:
a + ar = 16
To find the sum to infinity, we can use the formula:
Sum to infinity = a / (1 - r)
Given that the sum to infinity is 25, we have:
25 = a / (1 - r)
We now have two equations:
a + ar = 16
a / (1 - r) = 25
We can solve these equations simultaneously to find the possible values of 'a'.
From the first equation, we can factor out 'a' to get:
a(1 + r) = 16
Dividing both sides of the second equation by 25, we have:
a / (1 - r) = 1
We can rearrange this equation to get:
a = 1 - r
Substituting this expression for 'a' in the first equation, we get:
(1 - r)(1 + r) = 16
Expanding the equation, we have:
1 - r^2 = 16
Rearranging the terms, we get:
r^2 = -15
Since we are dealing with a geometric progression, the common ratio 'r' must be a real number. However, we observe that r^2 = -15 has no real solutions. Therefore, there are no possible real values for the first term 'a' that satisfy both equations.
for such more question on real value
https://brainly.com/question/27371101
#SPJ8