If an aircraft is present in a certain area, a radar correctly registers its presence with probability 0.99. if it is not present, the radar falsely registers an aircraft presence with probability 0.10. we assume that an aircraft is present with probability 0.05. what is the probability of false alarm (a false indication of aircraft presence), and the probability of missed detection (notng registers, even though an aircraft is present)? what is the probability that an aircraft is present given that the radar registers a presence?
Answers
Answer:
A) 0.005
B) 0.001
C)0.0495
Step-by-step explanation:
Let A be the event that an aircraft is present and let B be the event the radar registers its presence.. Thus;
P(A) = Probability that an aircraft is present
P(A') = Probability that an aircraft is not present
P(B) = Probability that the radar generates an alarm
P(B') = Probability that the radar doesn't generate an alarm
Thus from what we are given, we have;
P(A) = 0.05
P(A') = 0.95
P(B) = 0.99
P(B') = 0.01
P(B|A') = 0.1
A) Probability of a false alarm will be;
P(A' ∩ B) = P(A) × P(B|A')
P(A' ∩ B) = 0.05 × 0.1 = 0.005
B) probability of missed detection is;
0.1 × (1 - 0.99) = 0.001
C) probability that an aircraft is present given that the radar registers a presence will be;
P(A ∩ B) = P(A) × P(B)
P(A ∩ B) = 0.05 × 0.99
P(A ∩ B) = 0.0495
Related Questions
A fair coin is tossed 5 times. Compute the probability of tossing 5 heads in a row.
Answers
Answer:
50%
Step-by-step explanation:
There is 2 side out of 100% half is 50 :D gl and mb if its wrong!
Answer:
* Here we assume that the coin tossed is fair.
Probability of event A = # Favorable cases for event A/ # Exhaustive cases for event B
Where
Favorable cases means outcomes of an experiment that favors a particular event
Exhaustive cases means, number of total possible outcomes.
For tossing a coin one time:
# Favorable cases = 1 (getting head)
# Exhaustive cases = 2 (two outcomes, say, head and tail)
So, P(getting head in a single toss) = 1/2
For tossing a coin two times:
# Favorable cases = 1 (getting 2 heads, say, HH)
# Exhaustive cases = 2*2 or 2^2 (4 outcomes, say, HH, HT, TH, TT)
So, P(getting 2 heads in two tosses of a coin) = 1/4
Similarly, for tossing a coin five times:
# Favorable cases = 1 (getting 3 heads, say, HHHHH)
# Exhaustive cases = 2*2*2*2*2 or 2^5 (32 outcomes, say, HHHHH, THHHH, ..... etc)
So, P(getting head in 5 tosses of a coin) = 1/32
Step-by-step explanation:
In a park, the ratio of adults to children is 11 to 9. If there are 320 people in the park, how many children are there?
Answers
Answer:
144
Step-by-step explanation:
320 ÷ 20 = 16
adults : children
11 : 9
9×16 = 144
10in 8 in 8 in What is the surface area of the solid? A. 384 square inches B. 184 square inches C. 192 square inches D. 224 square inches
Answers
Answer:
Step-by-step explanation:
224 sq in.
A bucket contains 72 red, 48 blue, 48 green, and 48 yellow crayons. The art teacher also has 120 pieces of drawing paper. What is the largest number of identical kits the art teacher can make with all of the crayons and all of the paper?
Answers
The art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper for proper distribution.
To determine the largest number of identical kits the art teacher can make using all the crayons and drawing paper, we need to find the greatest common divisor (GCD) of the quantities.
The GCD represents the largest number that can divide all the quantities without leaving a remainder.
The GCD of the quantities of crayons can be found by considering the prime factorization:
72 = 2³ × 3²
48 = 2⁴ × 3
48 = 2⁴ × 3
48 = 2⁴ × 3
The GCD of the crayons is 2³ × 3 , which is 24.
Now, we need to find the GCD of the quantity of drawing paper:
120 = 2³ × 3 × 5
The GCD of the drawing paper is also 2³ × 3 , which is 24.
Since the GCD of both the crayons and drawing paper is 24, the art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper.
Each kit would contain an equal distribution of crayons and drawing paper.
Learn more about distribution here:
brainly.com/question/30034780
#SPJ1
Walmart was having a sale on video games. They offered a 15% discount on a game that was originally priced at $30. After the sale, the discounted price of the game was increased by 10%. What is the new price of the game after this increase?
Answers
Answer:
28.05$
Step-by-step explanation:
The game got a discount of 15%.
New price is (30$) ( 0.85 ) = 25.5$ (since the discount is 15% you only pay for the 85% of the original price)
Then an increase of 10%. this is:
New price: 25.5$ (1.10) = 28.05
New price is 28$ with 5 cents
Two parallel lines are crossed by a transversal.
What is the value of d?
Answers
The value of d in the image that shows the two parallel lines that are crossed by the transversal is determined as: 125°.
What is a Transversal?In geometry, a transversal is a line that intersects two or more other lines at distinct points. When a transversal intersects a pair of parallel lines, it creates various angles and relationships between those angles.
The image attached below shows the two parallel lines which are crossed by the transversal, where angle d and 125° are vertical angles.
Since they are vertical angles, they will be equal or congruent to each other. Therefore, the value of d = 125°
Learn more about Transversal on:
https://brainly.com/question/24607467
#SPJ1

The angle formed between one side and another, always less than 180 degrees.
Answers
Answer:obtuse angle
Step-by-step explanation:
An obtuse angle is an angle of greater than 90° and less than 180°. It is bigger than an acute angle. It is smaller than a straight angle, which measures 180°. Angles are measured with a protractor obtuse angle is specifically present in hexagon and pentagon and others.
JKLM is a rhombus.
m/JMN = (-x+69)*
mZLMJ = (-6x +166)
K
N
M
Find the mZLKN.
label optional

Answers
The angle LKN in the rhombus is 62 degrees.
How to find angles in a rhombus?A rhombus is a quadrilateral that has 4 sides equal to each other. The sum of angles in a rhombus is 360 degrees.
Opposite angles are equal in a rhombus. The diagonals bisect each other at 90 degrees. Adjacent angles add up to 180 degrees.
Therefore, let's find ∠LKN as follows:
m∠JMN = (-x + 69)
m∠LMJ = (-6x + 166)
Therefore,
1 / 2 (-6x + 166) = -x + 69
-3x + 83 = -x + 69
-3x + x = 69 - 83
-2x = -14
x = -14 / -2
x = 7
Therefore,
∠LKN = 1 / 2 (-6x + 166)
∠LKN = 1 / 2 (-6(7) + 166)
∠LKN = 1 / 2 (-42 + 166)
∠LKN = 62 degrees
learn more on rhombus here: https://brainly.com/question/30995617
#SPJ1
A quality control expert at LIFE batteries wants to test their new batteries. The design engineer claims they have a variance of 2916 with a mean life of 518 minutes.
If the claim is true, in a sample of 81 batteries, what is the probability that the mean battery life would be less than 526.4 minutes? Round your answer to four decimal places.
Answers
The probability that the mean battery life would be greater than 526.4 minutes if in a sample of 81 batteries having a variance of, 2916 and a mean life of 518 minutes is 0.0808.
What is probability?The ratio of good outcomes to all possible outcomes of an event is known as probability. A lot of successful results for an experimental with 'n' results can be represented by the symbol x.
Given:
The variance = 2916,
The mean life of a battery, m = 518 min,
The total number of samples, n = 81
Calculate the probability of a mean battery life of lower than 526.4 minutes by the following formula,
z = x - m / (σ / √ n)
Here, x is the expected value, σ is the deviation, and z is the probability.
Substitute the values,
z = 526.4 - 518 / (54 / √81) [σ = √ variance = √2916 = 54]
z = 1.4
Consult the cumulative standard normal table
P (z < 526.4) = 0.9192,
But we know that
P (z > 526.4) = 1 - P (z < 526.4)
P (z > 526.4) = 1 - 0.9192 = 0.0808
Therefore, The probability that the mean battery life would be greater than 526.4 minutes if in a sample of 81 batteries having a variance of, 2916 and a mean life of 518 minutes is 0.0808.
To know more about probability:
https://brainly.com/question/743546
#SPJ1
Find x. √11 X = √17 VIRI X
Answers
1.243 is the measure of the value of x from the given expression
Solving rational equationsRational equations are those that contain rational expressions. A rational expression is a fraction with polynomial numerator and denominator. A rational expression, in other terms, is a ratio between two polynomials.
Given the following rational equation
√11 x = √17
We need to determine the measure of the value of x.
Taking the square of both sides we will have:
(√11 x)² = (√17)²
11x² = 17
x² = 17/11
x² = 1.545
Take the square root of both sides
√x² = √1.545
x = 1.243
Hence the measure of the value of x from the given equation is 1.243.
Learn more on rational equation here: https://brainly.com/question/12223525
#SPJ1
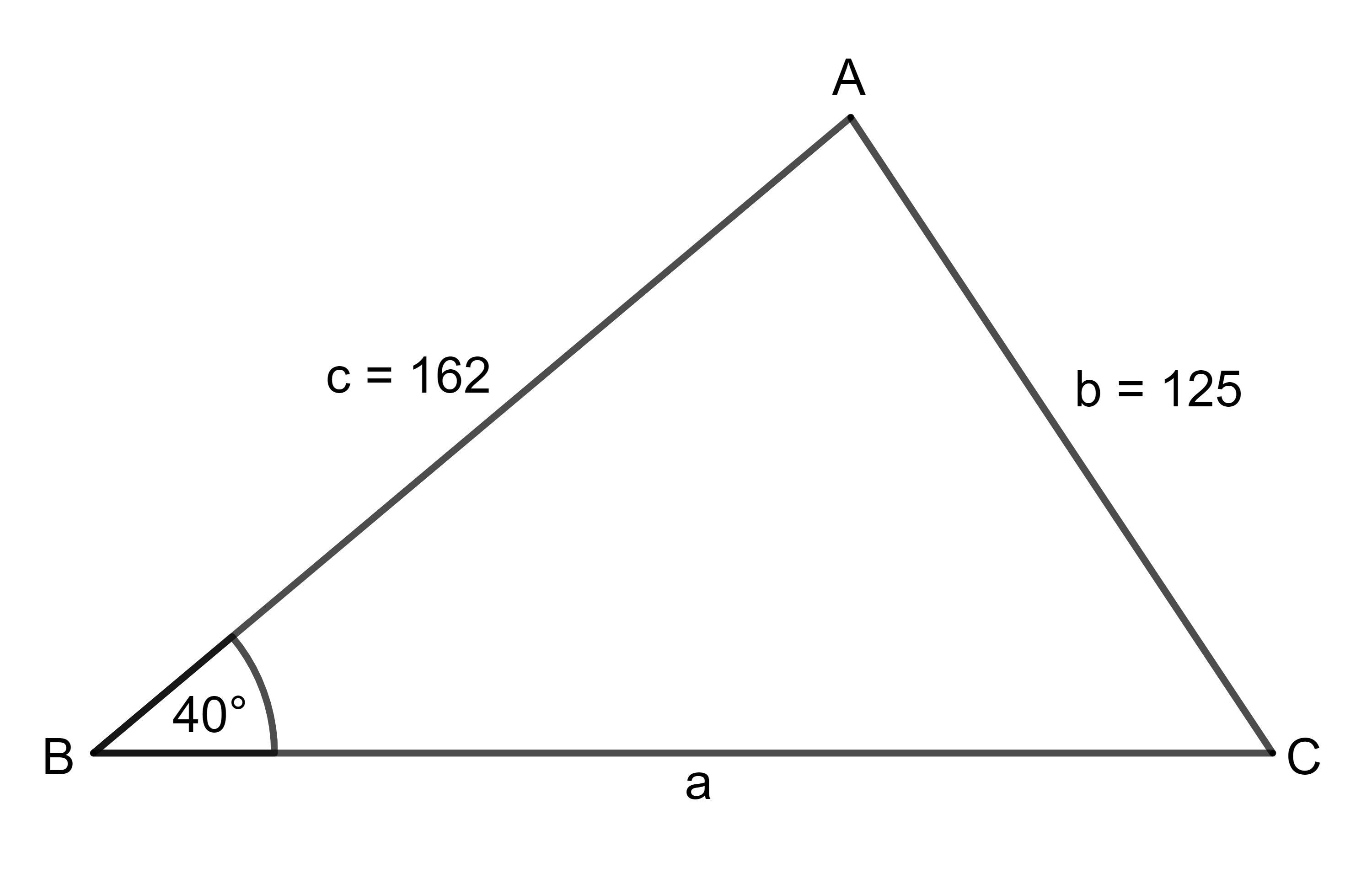
How do you solve a triangle ABC where b=125 c=162 B=40 degrees?
Answers
Answer:
Angle A = 83.59° (2 d.p.)
Angle C = 56.41° (2 d.p.)
Side a = 193.25 (2 d.p.)
Step-by-step explanation:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Sine Rule} \\\\$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Given:
b = 125c = 162B = 40°Substitute the given values into the Sine Rule formula:
\(\implies \dfrac{\sin A}{a}=\dfrac{\sin 40^{\circ}}{125}=\dfrac{\sin C}{162}\)
Solve for angle C:
\(\implies \dfrac{\sin 40^{\circ}}{125}=\dfrac{\sin C}{162}\)
\(\implies \sin C=\dfrac{162\sin 40^{\circ}}{125}\)
\(\implies C=\sin^{-1}\left(\dfrac{162\sin 40^{\circ}}{125}\right)\)
\(\implies C=56.4136175...^{\circ}\)
Interior angles of a triangle sum to 180°. Therefore:
\(\implies A+B+C = 180^{\circ}\)
\(\implies A = 180^{\circ}-B-C\)
\(\implies A = 180^{\circ}-40^{\circ}-56.4136175...^{\circ}\)
\(\implies A = 83.5863824...^{\circ}\)
Finally, to find a, substitute the found angles and sides into the Sine Rule and solve for a:
\(\implies \dfrac{\sin A}{a}=\dfrac{\sin B}{b}\)
\(\implies \dfrac{\sin 83.5863824...^{\circ}}{a}=\dfrac{\sin 40^{\circ}}{125}\)
\(\implies a=\dfrac{125\sin 83.5863824...^{\circ}}{\sin 40^{\circ}}\)
\(\implies a=193.248396...\)
Convert 80 miles an hour to 40 feet per second?
Answers
1 hour= 3600 sec
422,400/3600= 117.33 ft/sec
what two numbers multiply to equal -50 but adds up to equal 5
Answers
Answer:
10 and -5
Step-by-step explanation:
x + y = 5
xy = -50
y = 5 - x
x(5-x) = -50
5x - x^2 = -50
x^2 - 5x - 50 = 0
from there on we can solve the classic way
\(\Delta = (-5)^2 - 4\cdot1\cdot(-50) = 25 + 200 = 225\\\sqrt{\Delta} = 15\\x_1 = \frac{5 - 15}{2} = -5\\x_2 = \frac{5+15}{2} = 10\\y_1 = 5 - x_1 = 10\\y_2 = 5 - x_2 = -5\)
Everything checks out.
Answer:
-5 × 10 = -50
-5 + 10 = 5
brainliest
URGENT PLEASE
One number is 5 more than two times the other. Their sum is 11.
Answers
Answer:
the numbers are 8 and 3.
From the observation deck of a skyscraper, Bentley measures a 48° angle of depression to a ship in the harbor below. If the observation deck is 969 feet high, what is the horizontal distance from the base of the skyscraper out to the ship? Round your answer to the nearest tenth of a foot if necessary.
Answers
With angle of depression = 48°, the horizontal distance from the base of the skyscraper to the ship is approximately 1239.8 feet.
What exactly is an angle of depression?An angle of depression is an angle formed by a horizontal line and a line of sight that is directed downward to an object or point below the horizontal line. In other words, it is the angle between a horizontal line and a line of sight that is directed downward from an observer to an object that is at a lower level than the observer.
Now,
We know that the tangent of the angle of depression A is equal to the opposite side (h) divided by the adjacent side (the distance from the observation deck to the ship). So we can set up an equation:
tan(A) = h / x
where x is the distance from the base of the skyscraper to the ship (the adjacent side).
x = h / tan(A)
A = 48 degrees (angle of depression)
h = unknown
x = unknown
tan(48) = 1.1106 (tangent of 48 degrees)
Using the equation above, we can solve for h:
h = x * tan(A)
h = 969 ft / tan(48)
h ≈ 1239.8 ft
So the horizontal distance from the base of the skyscraper to the ship is approximately 1239.8 feet.
To know more about angle of depression visit the link
https://brainly.com/question/13697260
#SPJ1

I am a trapezium, identify my properties from the following:
a. my opposite sides are parallel // b. I am a quadrilateral // c. I have all the sides equal
Answers
a. my opposite sides are parallel
FALSE. Only the basis sides are parallel.
b. I am a quadrilateral
TRUE. A trapezium has 4 sides.
c. I have all the sides equal
FALSE. The trapezium is a special shape in that it does not, unlike the square or rectangle, have to have any equal side lengths.
What will be the new position of the given point (3, 5) after translation of 2 units left and 3 units up?
Answers
Answer:5 8
Step-by-step explanation:left 2 up 3
Which one of the following correctly states the VaR for a 3-year period with a 2.5 percent probability?
a) Prob[Rp, I E(Rp) x 3 - 1.960 x Op V3]
b) Prob[Rp, I S E(Rp) x 13 - 1.645 x Op 3]
c) Prob[Rp, T = E(Rp) x V3 - 1.960 x Op 3]
Answers
Answer: Option A
Prob[Rp,T ≤ E(Rp) × 3 - 1.960 × σp √3]
Step-by-step explanation:
It should be noted that, the VaR for a 3-year period with a 2.5 percent probability is Prob[Rp,T ≤ E(Rp) × 3 - 1.960 × σp √3]. Therefore, option A only is correct while other options are wrong
Answer:
A: Prob[Rp, I E(Rp) x 3 - 1.960 x Op V3]
Step-by-step explanation:
Vrite an equation of the parabola in vertex form.
1. passes through (-5, 0) and has vertex
(-2, 1)
Answers
The equation of the parabola in vertex form is equal to the quadratic equation y - 1 = - (1 / 9) · (x + 2)².
How to find the equation of the parabola based on two given points
Mathematically speaking, parabolae are represented by quadratic equations, there different forms of the equation of the parabola. In this case, we must use the vertex form, whose description is shown below:
y - k = C · (x - h)²
Where:
(h, k) - Coordinates of the vertex.C - Vertex constant.If we know that (x, y) = (- 5, 0) and (h, k) = (- 2, 1), then the equation of the parabola in vertex form is:
(0 - 1) = C · (- 5 + 2)²
- 1 = 9 · C
C = - 1 / 9
y - 1 = - (1 / 9) · (x + 2)²
To learn more on parabolae: https://brainly.com/question/21685473
#SPJ1

Help with the following equation 8x²-6x-5=x
Answers
Answer:
\(8 {x}^{2} - 6x - 5 = x\)
\(8 {x}^{2} - 7x - 5 = 0\)
x = (7 + √((-7)^2 - 4(8)(-5)))/(2×8)
= (7 + √(49 + 160))/16
= (7 + √209)/16
= -.4661, 1.3411 (to 4 decimal places)
Divide the following and round to the nearest hundredth: 0.8931/3
Answers
Which number is between - and 1.5?
A. 1 3/4
B. 0
C. -5/8
D. -0.6
!!!!!!!!!!!!!!!!!!!1
Answers
Answer:
Possibly A, cause you didn't give the first number.
4, 12, 36,what is 3 other remaining sequence
Answers
Answer:
108, 324, 972
Step-by-step explanation:
This sequence is multiplying by ✖️3.
4✖️3=12✖️3=36✖️3=108✖️3=324✖️3=972
Hope this helps!
Exercise #14: The mile and the kilometer are relatively close in size. Can you convert 1 mile into an equivalent
in kilometers? Here's what I'll give you. There are 2.54 centimeters in an inch, 5,280 feet in a mile, 100
centimeters in a meter, and 1000 meters in a kilometer. All else you should be able to do for yourself. Round
your answer to the nearest tenth of a kilometer. This takes quite a string of multiplications, but you can do it!
Answers
The equivalent of 1 mile to kilometres is approximately 1.6 km.
2.54 cm = 1 inch
5280 ft = 1 mile
100 cm = 1 m
1000 m = 1 km
Using the information let's convert 1 mile to kilometre.
1000 m = 1 km
Therefore,
1 m = 0.000621371 miles
1000 m(1 km) = ?
cross multiply
length = 1000 × 0.000621371 = 0.621371 miles
Therefore,
0.621371 miles = 1 km(1000 m)
1 miles = ?
length in km = 1.60934449789 km
Therefore,
1 miles = 1.6 km
learn more here; https://brainly.com/question/14035504?referrer=searchResults
Country A has an exponential growth rate of 4.3% per year. The population is currently 4,079,000, and the land area of Country A is 19,000,000,000 square yards. Assuming this growth rate continues and is exponential, after how long will there be one person for every square yard of land?
Answers
The number of years it would it take for there to be one person for every square yard is 108,325.68 years.
How many years would it take for there to be one person for every square yard?When there is one person for every square yard, it means that the population and land area are equal in value.
Number of years = (In FV / PV) / r
FV = future populationPV = present populationr = rate of growth(In 19 billion / 4,079,000) / 0.043 = 108,325.68 years
To learn more about exponential functions, please check: brainly.com/question/26331578
Burning Brownie has five varieties of cakes as Chocolate fudge cake (Cake 1), Nutella-filled Cake (Cake 2), Marble Cake (Cake 3), Cheese cake (Cake 4) and Fruit Cake (Cake 5) at their store. The selling prices of each of the cakes are $9, $12, $4, $5, $8 respectively. a. Formulate the Revenue function If it takes 4 cups of milk, 7 cups of sugar, 1 egg, 3 cups flour & 4 cups cream to make Cake 1; 3 cups milk, 4 cups sugar, 2 egg, 4 cups flour & no cream to make Cake 2; 1 cups milk, 5 cups sugar, 3 eggs, 2 cups flour & 1 cup cream to make Cake 3; 5 cups milk, no sugar, 4 eggs, 4 cups flour & 5 cups cream for Cake 4; & lastly 4 cups milk, 8 cups sugar, 5 eggs, 6 cups flour & 3 cups cream to make Cake 5; Which types of cakes to be baked such that we get maximum Revenue? Keep in mind that the store has availability of maximum 280 cups milk, 300 cups sugar, 80 eggs, 250 cups flour & 190 cups cream at their disposal. b. Formulate the constraints of the scenario. c. Solve the system if linear inequalities using Excel Solver.
Answers
A. In equation form: Revenue = 9x1 + 12x2 + 4x3 + 5x4 + 8x5
B. Non-negativity constraint: x1, x2, x3, x4, x5 ≥ 0
How did we get these values?To solve this problem using E x c e l Solver, set up the revenue function and the constraints. Here's how you can do it:
a. Revenue Function:
Let's denote the number of cakes baked for each type as x1, x2, x3, x4, and x5 respectively.
The revenue function can be formulated as:
Revenue = (Selling Price of Cake 1 × Number of Cake 1) + (Selling Price of Cake 2 × Number of Cake 2) + (Selling Price of Cake 3 × Number of Cake 3) + (Selling Price of Cake 4 × Number of Cake 4) + (Selling Price of Cake 5 × Number of Cake 5)
In equation form:
Revenue = 9x1 + 12x2 + 4x3 + 5x4 + 8x5
b. Constraints:
The constraints for the availability of ingredients can be formulated as follows:
Milk constraint: 4x1 + 3x2 + x3 + 5x4 + 4x5 ≤ 280
Sugar constraint: 7x1 + 4x2 + 5x3 ≤ 300
Egg constraint: x1 + 2x2 + 3x3 + 4x4 + 5x5 ≤ 80
Flour constraint: 3x1 + 4x2 + 2x3 + 4x4 + 6x5 ≤ 250
Cream constraint: 4x1 + 5x3 + x4 + 3x5 ≤ 190
Non-negativity constraint: x1, x2, x3, x4, x5 ≥ 0
c. Solve the system of linear inequalities using E x c e l Solver:
To solve the system of linear inequalities using E x c e l Solver, follow these steps:
1. Open M i c r o s o f t E x c e l and enter the following data in a new sheet:
| | A | B |
|-----|-----------|-----------------|
| 1 | Cakes | Selling Price |
| 2 | Cake 1 | $9 |
| 3 | Cake 2 | $12 |
| 4 | Cake 3 | $4 |
| 5 | Cake 4 | $5 |
| 6 | Cake 5 | $8 |
| | | |
| | | Formula |
| 9 | Milk | 280 |
| 10 | Sugar | 300 |
| 11 | Eggs | 80 |
| 12 | Flour | 250 |
| 13 | Cream | 190 |
2. In cell B16, enter the formula for the revenue:
=B2×B7 + B3×B8 + B4×B9 + B5×B10 + B6×B11
3. In cell B18, enter the formula for the milk constraint:
=4×B2 + 3×B3 + B4 + 5×B5 + 4×B6
4. In cell B19, enter the formula for the sugar constraint:
=7×B2 + 4×B3 + 5×B4
5. In cell B20, enter the formula for the egg constraint:
=B2 + 2×B3 + 3×B4 + 4×B5 + 5×B6
6. In cell B21, enter the formula for the flour constraint:
=3×B2 + 4×B3 + 2×B4 + 4×B5 + 6×B6
7. In cell B22, enter the formula for the cream constraint:
=4×B2 + 5×B4 + B5 + 3×B6
8. In cell B24, enter the formula for the non-negativity constraint for Cake 1:
=B2
9. Repeat step 8 for the remaining cakes, entering the formulas in cells B25, B26, B27, and B28:
=B3
=B4
=B5
=B6
10. Now, select cells B16 to B28 and click on the "Solver" button in the "Data" tab.
11. In the Solver Parameters window, set the objective to maximize the cell B16 (Revenue).
12. Set the By Changing Variable Cells to B24:B28 (the number of cakes baked).
13. Click on the "Add" button in the "Subject to the Constraints" section.
14. In the Constraint window, select the range B18:B22 for the constraint cells.
15. In the Solver Parameters window, click on the "Add" button again and select the range B24:B28 for the non-negativity constraints.
16. Set the Solver options as desired, and click on the "Solve" button.
E x c e l Solver will calculate the optimal values for the number of cakes to be baked for each type that maximize the revenue, while satisfying the given constraints on ingredient availability. The solution will be displayed in cells B24:B28, indicating the number of cakes to be baked for each type.
learn more about excel solver: https://brainly.com/question/31404959
#SPJ1
These tables represent a quadratic function with a vertex at (0,3). What is the
average rate of change for the interval from x = 7 to x = 8?
х
Interval
0
1
2
у
3
2
-1
-6
-13
--22
--33
Average rate
of change
-1
1-2
-3
1-2
-5
1-2
-7
]-2
-9
13-2
-11
O to 1
1 to 2
2 to 3
3 to 4
4 to 5
5 to 6
3
4
5
6
O
A. -15
B. -61
C.-2
D. -46
Answers
Answer:
These tables represent a quadratic function with a vertex at (0,-1) what is the average rate of change for the interval from x=7 to x=8?
B.-15
Step-by-step explanation:
The average rate of change from 7 to 8 = -15
How to determine the average rate of change?The average rate of change of a quadratic function is calculated using:
Rate = (f(b) - f(a))/(b - a)
The interval is from x = 7 to 8.
So, we have:
(a,b) = (7,8)
The equation becomes
Rate = (f(8) - f(7))/(8 - 7)
Evaluate the difference
Rate = (f(8) - f(7))/1
This gives
Rate = f(8) - f(7)
From the table, we have:
Rate from 5 to 6 = -11 where the constant is -2
So, we have:
Rate from 6 to 7 = -11 - 2
Rate from 6 to 7 = -13
Also, we have:
Rate from 7 to 8 = -13 -2
Rate from 7 to 8 = -15
Hence, the average rate of change from 7 to 8 = -15
Read more about average rate of change at:
https://brainly.com/question/8728504
3. How many subsets will the set below have?
T= {Monday, Tuesday, Wednesday, Thursday, Friday)
A5
B. 10
C. 32
D.64
Answers
Explanation:
There are n = 5 items in set T
This means there are 2^n = 2^5 = 32 subsets
X
Solve for x.
10 cm
20°
X = [?] cm
Round to the nearest hundredth
![XSolve for x.10 cm20X = [?] cmRound to the nearest hundredth](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/MsP3iAXadvYBF9I1oxD6piUqb8nB5TDr.png)
Answers
Answer:
x = 9.40 cm
Step-by-step explanation:
Since it's a right triangle, we can then use pythagorean theorem to find the value of x.
Use cosine function.
\(cos \alpha = \frac{adjacent}{hypotenuse} \\cos 20 = \frac{x}{10cm} \\x = 10cos20 \\x = 9.40 cm\)
The length of the side, x in the given right-angled triangle with 10 cm length of hypotenuse is 6.82 cm.
The problem is asking us to find the length of the missing side of a right triangle. The given information is the length of one leg (10 cm) and the measure of one of the acute angles (20°).
We can use the sine function to solve for the missing side. The sine function is the ratio of the opposite side to the hypotenuse of a right triangle. In this case, the opposite side is the missing side, and the hypotenuse is the side that is opposite the right angle.
The following equation can be used to solve for x:
sin(20°) = x / 10
We can solve for x by multiplying both sides of the equation by 10 and then using a calculator to evaluate the expression. The answer is x = 6.82 cm.
To round the answer to the nearest hundredth, we can use the following steps:
Find the hundredths place of the answer, which is 2.
Look at the digit to the right of the hundredths place, which is 8.
If the digit to the right of the hundredths place is 0, 1, 2, 3, 4, or 5, then the hundredths place is rounded up.
If the digit to the right of the hundredths place is 6, 7, 8, or 9, then the hundredths place is rounded up to the next digit.
In this case, the digit to the right of the hundredths place is 8, so the hundredths place is rounded up to 9. Therefore, the rounded answer is x = 6.82 cm.
To learn more about length here:
https://brainly.com/question/3199583
#SPJ2
If EH = 18 and FG 1 EH, solve for the measure of EG.

Answers
Answer:
9
Step-by-step explanation:
If its perpendicular, it probably bisects EH, so just split it in half.