If m ∠ F L G = 14 x + 5 ° and m ∠ H L G = 17 x − 1 ° , find m ∠ F L H .
Answers
The value of ∠ F L H is 3x-6°
∠FLG and ∠FLH are adjacent angles with L being the common vertex and both the angles form the ∠HLG
As ∠FLG is given as 14x + 5° and ∠ H L G is given as 17 x − 1 °
We need to find the value of ∠ F L H
We can write that ∠FLG +∠FLH = ∠ H L G
by putting the values given
14 x + 5 ° + ∠ F L H = 17 x − 1 °
∠ F L H = 17x-1 - (14x + 50
Here we got a linear equation in one variable and by solving the equation we will get the value of ∠ F L H
∠ F L H = 17x - 1 - 14x -5
∠ F L H = 3x-6
Hence, the value of ∠ F L H is 3x-6°
To know more about linear equation- https://brainly.com/question/13738061
#SPJ9
Related Questions
Introduction to Probability
Please show all work
Suppose you are taking an exam that only includes multiple choice questions. Each question has four possible choices and only one of them is correct answer per question. Questions are not related to the material you know, so you guess the answer randomly in the order of questions written and independently. The probability that you will answer at most one correct answer among five questions is
Answers
The probability of guessing the correct answer for each question is 1/4, while the probability of guessing incorrectly is 3/4.
To calculate the probability of answering at most one correct answer, we need to consider two cases: answering zero correct answers and answering one correct answer.
For the case of answering zero correct answers, the probability can be calculated as (3/4)^5, as there are five independent attempts to answer incorrectly.
For the case of answering one correct answer, we have to consider the probability of guessing the correct answer on one question and incorrectly guessing the rest. Since there are five questions, the probability for this case is 5 * (1/4) * (3/4)^4.
To obtain the probability of answering at most one correct answer, we sum up the probabilities of the two cases:
Probability = (3/4)^5 + 5 * (1/4) * (3/4)^4.
Therefore, by calculating this expression, you can determine the probability of answering at most one correct answer among five questions when guessing randomly.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
6.09 to the nearest tenth.
Answers
Answer:
6.1
Step-by-step explanation:
So when rounding off to the earest tenth check if the hundredeth number is bigger than 5 in this case the 9 is bigger than 5.
Because it is bigger than 5 add a 1 to the tenth unit making it 1.
Leave the 6 as it is.
The answer then becomes 6.1
HOPE THIS HELPED
In a region where there is a uniform electric field, the potential, v1, is 1. 3 v at position y1=26 cm. At position y2=28 cm , the potential, v2, is 3. 9 v. What is the change in electric potential energy of an alpha particle (charge = +2e) if it is moved from y1 to y3?.
Answers
The change in electric potential energy of an alpha particle is:
1.3V/cm
"Information available from the question"
In a region where there is a uniform electric field, the potential, v1, is 1. 3 v at position y1=26 cm.
At position y2=28 cm , the potential, v2, is 3. 9 v.
Now, According to the question:
Calculation of magnitude:
Since V1 is 1.3 V at position y1=26 cm. At position y2=28 cm, the potential, V2, is 3.9 V
So, We know that
\(E =\frac{V_2-V_1}{Y_2-Y_1}\)
\(E=\frac{3.9-1.3}{28-26}\)
\(E=\frac{2.6}{2}\)
E = 1.3V/cm
Learn more about Magnitude at:
https://brainly.com/question/14452091
#SPJ4
At a coffee shop, the amount of tax due is calculated based on the cost of the customer's
order.
t = the amount of tax due
c = the cost of the order
Which of the variables is independent and which is dependent?
Answers
In this context, the dependent variable is t (amount of tax due) and the independent variable is c (cost of the order).In this scenario, the variables are t (the amount of tax due) and c (the cost of the order).
To determine which variable is independent and which is dependent, we need to understand their relationship.In this case, the amount of tax due, t, is calculated based on the cost of the customer's order, c. The tax amount is dependent on the cost of the order because it is directly influenced by the value of c. As the cost of the order changes, the amount of tax due will also change accordingly.
On the other hand, the cost of the order, c, is independent. It is not influenced or determined by the amount of tax due. The customer can choose the cost of their order, and the tax will be calculated based on that chosen amount.
For more such questions on variable
https://brainly.com/question/27894163
#SPJ8
What is the factorization of 81a6 - 100? (9a2 − 10)(9a3 + 10) (9a2 − 10)(9a3 − 10) (9a3 − 10)(9a3 + 10) (9a3 − 10)(9a3 − 10)
Answers
Answer:
(9a³ − 10)(9a³ + 10)
Step-by-step explanation:
Difference of squares
(9a³ − 10)(9a³ + 10)
Answer:
What is the factorization of 81a6 - 100?
(9a2 − 10)(9a3 + 10) (9a2 − 10)(9a3 − 10) (9a3 − 10)(9a3 + 10) <<< CORRECT (9a3 − 10)(9a3 − 10)
Step-by-step explanation:
Oct 2021 Edge
Una carretera recta forma un angulo de 22° con la horizontal dde cierto punto Q en ella el angulo de elevacion del avion en el punto A 57 en el mismo instante dde otro punto Q a 100 m adelante del primero el angulo de elevacion 63 los puntos P Q A quedan en el plano vertical calcule la distancia de P al avion
Answers
The distance from P to the airplane is y = x + 100 ≈ 628.38 m.
What is the triangle?A triangle is a three-sided polygon with three angles. It is a fundamental geometric shape and is often used in geometry and trigonometry.
From a certain point Q on a straight road, which forms an angle of 22° with the horizontal, the angle of elevation of an airplane at point A is 57°. At the same instant from another point Q, 100 meters ahead of the first point, the angle of elevation of the airplane is 63°. The points P, Q, and A are in the same vertical plane. Find the distance from P to the airplane.
To solve the problem, we can use the concept of similar triangles. Let's call H the height of the airplane and x the distance from Q to the airplane. Then, the distance from P to the airplane is given by y = x + 100.
From triangle QA1H, we have:
tan(57°) = H / x
From triangle QA2H, we have:
tan(63°) = H / (x + 100)
Dividing these two equations, we get:
tan(57°) / tan(63°) = x / (x + 100)
Solving for x, we get:
x = 100 * tan(63°) / (tan(63°) - tan(57°)) ≈ 528.38 m
Therefore, the distance from P to the airplane is:
y = x + 100 ≈ 628.38 m.
To learn more about Triangles from the given link:
https://brainly.com/question/2773823
#SPJ4
Aaron is baking cookies. The recipe uses 2 cups of flour to make 30 cookies. If Aaron wants to make 40 cookies, how many cups of flour should he use
plz answer asap.
Answers
Step-by-step explanation:
30 cookies = 2 cups
1 cookie = 2/30 cups = 1/15 cups
40 cookies = 1/15 × 40 = 8/3 cups
PLEASE HELP ME!!!
I have 5 pinks, 4 yellow, 3 orange, and 3 red starbursts. What is the probability that I will randomly pick a yellow starburst, put it back in the bag, and then randomly pick an orange starburst?
A. 7/15
B. 4/75
C. 4/15
D. 3/15
Answers
Answer:
B. 4/75
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
For each trial:
The probabilities of picking each startbust are the same, so each event is independent.
Independent events:
Two events, A and B, we have that:
\(P(A \cap B) = P(A) \times P(B)\)
In this question:
Event A: Yellow starburst on the first trial.
Event B: Orange starbust on the second trial.
4 yellow out of 5+4+3+3 = 15 starbursts.
This means that \(P(A) = \frac{4}{15}\)
3 orange out of 15 starbursts.
This means that \(P(B) = \frac{3}{15}\)
Probability of A, then B:
\(P(A \cap B) = P(A) \times P(B) = \frac{4}{15} \times \frac{3}{15} = \frac{4*3}{15*15} = \frac{4}{15*5} = \frac{4}{75}\)
So the correct answer is:
B. 4/75
In a town there are 1349 families if there are an average two children attending elementary School from each family and each school can accommodate 220 student children the minimum number of elementary schools needed in the region is 6 9 or 13
Answers
Answer:
13
Step-by-step explanation:
First find the number of children attending elementary school
= 1349*2
= 2698 children
Now each school can accommodate 220 children so divide the number of children by 220
= \(\frac{2698}{220}\)
= 12.26 which is the closest to 13 in the options so the answer is 13
There are 60 seats on a train. 35% of the seats are empty. How many empty seats are there on the train?
Answers
Answer:
21
Step-by-step explanation:
35% of 60=60% of 35
10% of 35=3.5
3.5*6=21
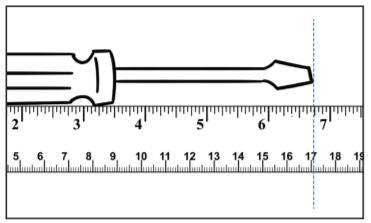
Measure the screwdriver's length to the nearest tenth of a centimeter. Express the answer as a decimal.
Answers
Answer:
17.1 cm
Step-by-step explanation:
A screw driver is a mechanical tool or device which is mainly used for screwing the screws and unscrewing them. It is also used for removing the nuts and bolts and also serves a variety of uses.
It is typically made of steel and has a handle and a shaft which ends as a tip.
In the context, the length of the screw driver from the given figure expressed to the nearest tenth of a centimeter is 17.1 cm.
It is also equivalent to \($6\frac{3}{4}$\) inch.
Find x so that GJ is parallel to FK if GF=12, HG=6, HJ=8, and JK=x-4.

Answers
Answer:
x=20
Step-by-step explanation:
(12+6)/(8+x-4) =6/8
18/(x+4)=6/8
6(x+4) =(18)(8)
(x+4) =(18)(8)/6
x+4 =(3)(8)
x+4=24
x=-4+24
x=20
n a basketball tournament, Team A scored 5 less than twice as many points as Team B. Team C scored 80 more points than Team B. The combined score for all three teams was 983 points. Let the variable b represent Team B’s total points. The equation representing this scenario is (2b – 5) + b + (b + 80) = 983. How many points did Team B score?
1. Combine like terms: 4b + 75 = 983
2. Use the subtraction property of equality: 4b = 908
3. Use the division property of equality: b =
Answers
Answer:
Let us assume number of points scored by Team B = b points.
Number of points scored by Team A 5 fewer than twice as many points as Team B, that is "5 less than 2b" = (2b-5) points .
Team C scored 80 more points than Team B, that is " 80 more than b" = (b+80) points.
Total number of points scored by all teams = 983 points.
Therefore, we can setup an equation:
(2b-5) + b + (b+80) = 983.
Therefore, an equation to represent this scenario using the variable b to represent Team B’s total points is (2b-5) + b + (b+80) = 983.
Step-by-step explanation:
Answer:
represent team b as b number of team a is five than twice as much point as team b=(2b_5)
team c scored 80 more than b that is (b+80) total number=983
so
.Learning Task 2: Get the quotient of each item up to the nearest ten thousandths place. Then, round the decimals to their nearest thousandths. Number 1 is done for you.
1.45÷8= 5.6250 -5.625------- example
4.93÷9 = _____ - ______
2. 77÷9 = _____ - ______
5.88 ÷7= _____ - ______
3.81÷7= _____ - ______
6.55÷8=_____ - ______
sorry if the numbers is a bit confusing
Answers
The responses for the quotient given to the nearest thousandths are
presented in the order of the of the questions as follows;
\(Question \ 4) \ \displaystyle \underline{\frac{93}{9} = 10.3333 \approx 10.333}}\)
\(Question \ 2) \ \displaystyle \underline{\frac{77}{9} = 8.5555 \approx 8.556}\)
\(Question \ 5) \ \displaystyle \underline{\frac{88}{7} = 12.4285 \approx 12.429}\)
\(Question \ 3) \ \displaystyle \underline{\frac{81}{7} = 11.5714\approx 11.571}\)
\(Question \ 6) \ \displaystyle \underline{\frac{55}{8} = 6.8750\approx 6.875}\)
Reasons:
4. The division is presented as follows;
\(\displaystyle \mathbf{\frac{93}{9}}= \frac{90 + 3}{9} = 10 + \frac{1}{3} = 10.\overline 3\)
Given that we have;
\(\displaystyle \frac{1}{3} = 0.\frac{10}{3} =0.3 \frac{10}{3} = 0.3333\)
Therefore;
\(\displaystyle \underline{\frac{93}{9} = 10.3333 \approx 10.333}\)
2. The division is presented as follows;
\(\displaystyle \mathbf{\frac{77}{9}} = \frac{72 + 5}{9} = 8 + \frac{5}{9} = 8. \frac{50}{9} = 8.5\frac{50}{9} = 8.55\frac{50}{9} = 8.555\frac{50}{9} = 8.5555\)
Therefore;
\(\displaystyle \underline{\frac{77}{9} = 8.5555 \approx 8.556}\)
5. The division is presented as follows;
\(\displaystyle \mathbf{\frac{88}{7}} = \frac{85 + 3}{7} = 12 + \frac{3}{7} = 12. \frac{30}{7} = 12.4\frac{20}{7} = 12.42\frac{60}{7} = 12.428\frac{40}{7} = 12.4285\frac{5}{7}\)
\(\displaystyle \underline{\frac{88}{7} = 12.4285 \approx 12.429}\)
3. The division is presented as follows;
\(\displaystyle \mathbf{\frac{81}{7}} = \frac{77 + 4}{7} = 11 + \frac{4}{7} = 11. \frac{40}{7} = 11.5\frac{5}{7} = 11.57\frac{10}{7} = 11.571\frac{30}{7} = 11.5714\frac{20}{7}\)
Therefore;
\(\displaystyle \underline{\frac{81}{7} = 11.5714\approx 11.571}\)
6. The division is presented as follows;
\(\displaystyle \mathbf{\frac{55}{8}} = \frac{48 + 7}{8} = 6 + \frac{7}{8} = 6. \frac{70}{8} = 6.8\frac{60}{8} = 6.87\frac{40}{8} = 6.875\frac{0}{8} =6.8750\)
Therefore;
\(\displaystyle \underline{\frac{55}{8} = 6.8750\approx 6.875}\)
Learn more here:
https://brainly.com/question/17913153
Given f(x) =4x +5, find f (-3).

Answers
Answer:
-7
Step-by-step explanation:
To find this out we just place -3 where x is
f(-3)=4(-3)+5
f(-3)= -12+5
f(-3)= -7
Hopes this helps please mark brainliest
what is the product of (-2x+6)(3x-4)
Answers
Answer:
\(-6x^2+26x-24\)Step-by-step explanation:
\((-2x+6)(3x-4)=\)\((-2x)(3x)-4(-2x)+6(3x)-6(4)=\)\(-6x^2+8x+18x-24=\)\(-6x^2+26x-24\)If $1 is 3% and $2 is 7% and w1 is 0.1, beta of the portfolio is
Answers
The beta of the portfolio, considering $1 with a beta of 3% and $2 with a beta of 7% and a weight of 0.1 (w1), is 6.6%.
The beta of a portfolio measures its sensitivity to overall market movements. To calculate the beta of a portfolio, we need the individual asset weights and betas of each asset. Given that $1 has a beta of 3% and $2 has a beta of 7%, with a weight of 0.1 (w1), we can determine the beta of the portfolio.
To calculate the beta of the portfolio, we use the following formula:
β(portfolio) = (w1 * β1) + (w2 * β2) + ...
In this case, the portfolio contains two assets, so the formula becomes:
β(portfolio) = (w1 * β1) + (w2 * β2)
Substituting the given values:
β(portfolio) = (0.1 * 3%) + (0.9 * 7%)
β(portfolio) = 0.3% + 6.3%
β(portfolio) = 6.6%
Therefore, the beta of the portfolio is 6.6%.
To know more about beta and its significance in portfolio management, refer here:
https://brainly.com/question/18760065#
#SPJ11
the difference of two variables x and y is 7. find two ordered pairs that satisty this equation if the values of y are 1 and 3... Show your solution
Answers
Answer:
The ordered pairs that are solution to this equation are:
(8,1) and (10,3)
Step-by-step explanation:
Given statement is:
"difference of two variables x and y is 7"
This can be mathematically written as:
\(x-y = 7\)
To solve this we have to put y = 1 and y = 3
Now,
Putting y = 1 in the equation
\(x-1 = 7\\x = 8\)
Putting y = 3 in the equation
\(x-3 = 7\\x = 7+3\\x = 10\)
Ordered pairs are of the form (x,y)
Hence,
The ordered pairs that are solution to this equation are:
(8,1) and (10,3)
Evaluate the triple integral ∭E4x dV where E is bounded by the paraboloid x=7y^2+7z^2 and the plane x=7.
Answers
The value of the triple integral ∭E 4x dV is 392/3.
To evaluate the triple integral ∭E 4x dV, we need to determine the limits of integration for each variable.
The region E is bounded by the paraboloid x = 7y^2 + 7z^2 and the plane x = 7. This means that the limits of integration for x are from 0 to 7, the limits of integration for y are from -sqrt((x-7)/7) to sqrt((x-7)/7), and the limits of integration for z are from -sqrt((x-7)/7) to sqrt((x-7)/7).
So the integral becomes:
∭E 4x dV = ∫₀⁷ ∫-sqrt((x-7)/7)ᵗsqrt((x-7)/7) ∫-sqrt((x-7)/7)ᵗsqrt((x-7)/7) 4x dz dy dx
= ∫₀⁷ ∫-sqrt((x-7)/7)ᵗsqrt((x-7)/7) 4x (2sqrt((x-7)/7)) dy dx
= 8 ∫₀⁷ ∫-sqrt((x-7)/7)ᵗsqrt((x-7)/7) (x-7)^(1/2) dy dx
= 8 ∫₀⁷ [(2/3)(x-7)^(3/2)]|₋s(qrt((x-7)/7)))^(qrt((x-7)/7)) dx
= 8 ∫₀⁷ (2/3)(x-7)^(3/2) dx
= 16/3 ∫₀⁷ (x-7) dx
= 16/3 [(1/2)(x-7)^2]|₀⁷
= 16/3 (49/2)
= 392/3
Therefore, the value of the triple integral ∭E 4x dV is 392/3.
To know more about integral refer here:
brainly.com/question/18125359#
#SPJ11
Lana wants to graph the height of an amusement park ride as it travels along the track.
A. The ride begins by climbing slowly up a hill.
B. It moves straight along a flat piece of track.
C. The ride glides quickly downhill.
D. It slowly climbs another hill.
Drag a segment to each box to show the shape of the graph for that interval.

Answers
Answer:
I can’t do this for you, you have to drag the segments into the boxes. The fifth over is A. then you do the first line segment. Then the third. for D you do the fifth over
Step-by-step explanation:
4 cm
4 cm
Use 3.14 this is hard I need help please thank youuu

Answers
The diameter is 4, meaning that the radius is 2. Pi r ^ 2 is what is the formula to find the area of a circle, and 2 squared is 4. 4 * 3.14 is 12.56. 12.56/2 is 6.28. 6.28 + 16 (4 * 4 is 16, which is the area of the square) is 22.28. I could be wrong but this is how I solved it.
What is the range of the relation below?
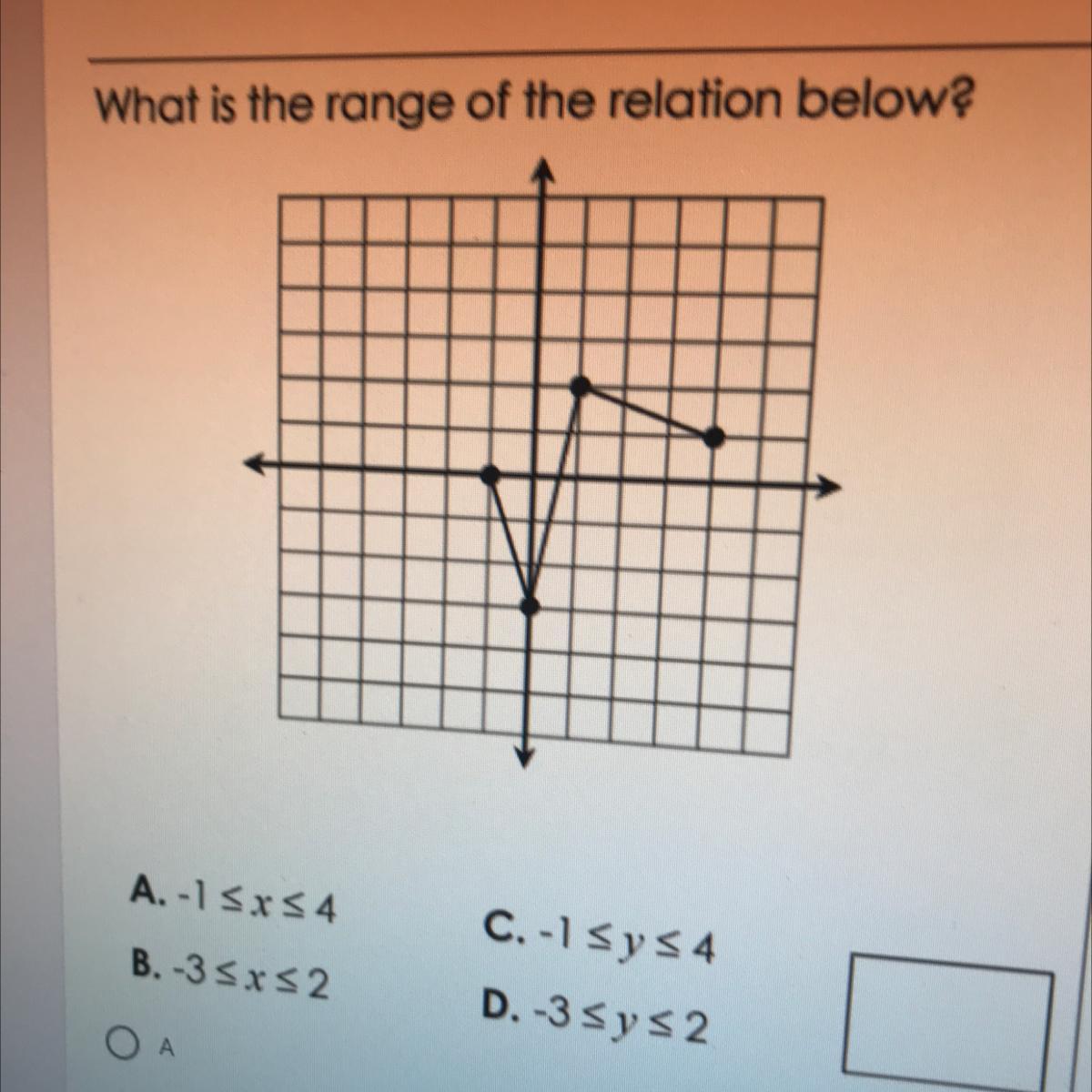
Answers
Answer:
D.
Step-by-step explanation:
because the lowest y is -3 and the highest is 2
In a group of students, 30% like Computer only, 25% like both Computer and Optional Maths and 5% don't like any of the subjects. If 390 students like Optional Maths, find the total number of students by drawing a Venn-diagram. (Ans: 600)
Answers
Answer:
Let's use a Venn diagram to solve this problem.
First, let's label the three regions of the Venn diagram: Computer only (C), Optional Maths only (M), and both Computer and Optional Maths (C ∩ M). We can also label the region outside the circles as neither Computer nor Optional Maths (N).
We know that 30% of the students like Computer only, which means that the percentage of students in region C is 30%. Similarly, 25% of the students like both Computer and Optional Maths, so the percentage of students in region C ∩ M is 25%.
We are also given that 5% of the students don't like either subject, so the percentage of students in region N is 5%.
Finally, we are told that 390 students like Optional Maths, which includes the students in regions M and C ∩ M. We don't know the percentage of students in region M, but we do know that the percentage of students in region C ∩ M is 25%.
Using this information, we can set up an equation to solve for the total number of students:
C + M + C ∩ M + N = 100%
Substituting the percentages we know, we get:
30% + M + 25% + 5% = 100%
Simplifying the equation, we get:
M = 40%
This means that 40% of the students like Optional Maths only, which is the percentage of students in region M.
Now we can use the fact that 390 students like Optional Maths to solve for the total number of students:
M + C ∩ M = 390
0.4T + 0.25T = 390
0.65T = 390
T = 600
Therefore, the total number of students is 600.
Determine the solution for x^2-3x-28=\> 0
Answers
Answer: x = -4 or x = 7
Step-by-step explanation:
x^2 - 3x - 28 =/>
(factor)
(x^2 + 4)(x-7) = 0
x + 4 = 0 or x - 7 = 0
(subtract -4 from 0 and 7 from 0)
x = -4 or x =7
Answer:
(infinity, -4] or [7, infinity).
Step-by-step explanation:
right on edge
Write the absolute value equations in the form |x-b|=c (where b is a number and c can be either a number or an expression) that have the following solution sets. Two solutions: x=2, x=14
Answers
Answer:
|x - 8| = 6
Step-by-step explanation:
|x - b| = c
⇒ (x - b)² = c²
Given:
x = 2x = 14Substitute the values of x into (x - b)² = c²:
(2 - b)² = c²
(14 - b)² = c²
Equate and solve for b:
(2 - b)² = (14 - b)²
⇒ 4 - 4b + b² = 196 - 28b + b²
⇒ 4 - 4b = 196 - 28b
⇒ 24b = 192
⇒ b = 8
Substitute b = 8 into the equations to find c:
x = 2 ⇒ |2 - 8| = 6
x = 14 ⇒ |14 - 8| = 6
Therefore, c = 6
Final equation: |x - 8| = 6
I\ need\ the\ answers\ for\ 6.07\ 8th\ grade\ on\ peak\ fueled
Answers
Answer:
what's the question that you need answered?
Step-by-step explanation:
?
correct answer will get brainliest.
31.
At noon, the temperature at a mountaintop research center is 11 degrees. Overnight the temperature drops to -19 degrees. Which expression represents how much the temperature changed?
a. |19|
b. |-19|
c. |-30|
d. |-38|
Answers
Answer:
c. |-30|
Step-by-step explanation:
It wants the change from 11 to -19. While normally absolute value is the distance from zero, zero can be shifted. Depending on where you are in learning about absolute value, the midway point can change from zero to, say, 4. This is called a transformation and is typically represented on a graph. Simple answer is that zero is shifted to 11. Therefore, absolute value changes from distance away from zero, to distance away from 11.
I hope this helped :)
3(x–6)–1/2(8x+10)=–25

Answers
The solution to the equation 3(x-6) - 1/2(8x+10) = -25 is x = 2.
To simplify the equation 3(x-6) - 1/2(8x+10) = -25, we can start by applying the distributive property and then combining like terms.
First, let's distribute the 3 and the -1/2 to the terms inside the parentheses:
3(x-6) - 1/2(8x+10) = 3x - 18 - (4x + 5)
Now, let's simplify further by combining like terms:
3x - 18 - 4x - 5 = -x - 23
So, the simplified equation is -x - 23 = -25.
To solve for x, we can isolate the variable by adding 23 to both sides of the equation:
-x - 23 + 23 = -25 + 23
This simplifies to:
-x = -2
Finally, we can solve for x by multiplying both sides of the equation by -1:
(-1)(-x) = (-1)(-2)
This gives us:
x = 2
Therefore, the solution to the equation 3(x-6) - 1/2(8x+10) = -25 is x = 2.
For more such questions on equation visit:
https://brainly.com/question/17145398
#SPJ8
if the probability of a is 0.45 and the probability of the intersection of a and b is 0.15, then the probability that b will occur given that a has occurred is:
Answers
The probability that b will occur given that a has occurred is 2/5 as the probability of a is 0.45 and the probability of the intersection of a and b is 0.15.
What is probability?It is based on the likelihood that something will occur. The justification for probability serves as the main foundation for theoretical probability. For instance, the theoretical chance of getting a head when tossing a coin is 12. Simply put, probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of various outcomes. Statistics is the study of events that follow a probability distribution.
Here,
P(A)=0.45
P(A∩B)=0.15
P(A∪B)=1
P(B)=1-(0.45+0.15)
=1-0.60
=0.4
=2/5
With a probability of 0.45 and a and b's intersection having a 0.15 probability each, the likelihood that b will happen given that a has happened is 2/5.
To know more about probability,
https://brainly.com/question/9793303?referrer=searchResults
#SPJ4
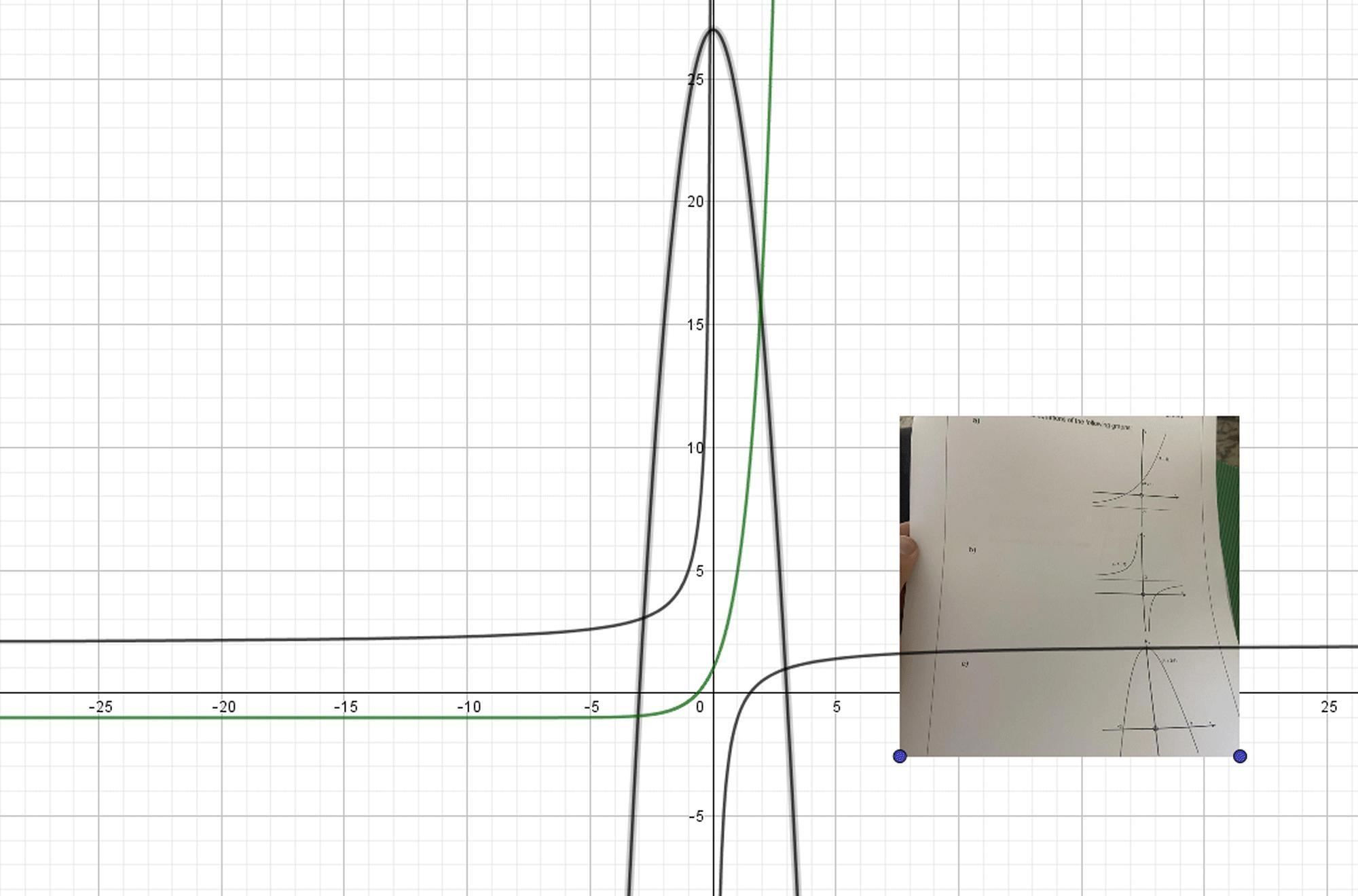
determine the equations of the following graphs

Answers
Answer:
Hello,
Step-by-step explanation:
a)
\(y=a^x*b+c\\\\if\ x- > -\infty,\ y- > -1 \ \Longrightarrow\ c=-1\\if\ x=0\ y=1\ \Longrightarrow\ 1=b-1\ \Longrightarrow\ b=2\\if\ x=1\ y=5 \ \Longrightarrow\ a*2-1=5\ \Longrightarrow\ a=3\\\\\boxed{y=2*3^x-1}\\\)
b)
\(f(x,y)=(x-a)(y-b)-k=0\ since\ hyperbola\ "\' equilat\`ere\ in\ French"\\\\\dfrac{\partial{f}}{\partial{x}} =y-b=0\ \Longrightarrow\ y=b\\\\\dfrac{\partial{f}}{\partial{y}} =x-b=0\ \Longrightarrow\ x=a\\\\Here\ center\ is\ (0,2)\ so (x-0)(y-2)=k\\\\(-3,3)\ is \ a\ point\ of \ the\ hyperbola:\\-3*(3-2)=k\ \Longrightarrow\ k=-3\\\\\boxed{x(y-2)=-3}\\\)
c)
It is parabola
y=k*(x-3)(x+3)
(1,24) is a point of the parabola:
24=k*(1²-9) => k=-3
\(\boxed{y=-3(x^2-9)}\\\)