If m/CDE is a straight angle, DE bisects m/GDH, mZGDE = (8x-1), m/EDH = (6x +
m/CDF = 43°, find each measure.
x =
m/GDH=
mZFDH=
m/FDE =
Answers
Answer:
From the way the problem is worded:
CDE is a straight angle made up of three angles: CDF of measure 43, FDG of unknown measure and GDE of measure 8x + 1.
EDH is outside CDE and is of measure 6x + 15.
Since DE bisects GDH to form GDE and EDH, those latter two angles are equal and thus 8x + 1 = 6x + 15 and x = 7 and substituting 7 for x, both angles are equal to 57 degrees.
Since CDF is 43 and GDE is 57 and CDE is 180 in total, then FDG = 180 - 43 - 57 = 80 degrees.
Related Questions
A political gathering in south america was attended by 8475 people each of south america's 12 countries and 3 territories was equally represented how many representatives attended from each country
Answers
Political sessions were attended by 707 representatives from all of South America.
What is meant by Ratios?Ratios: A ratio is an ordered pair of numbers a and b, written a / b where b does not equal 0. A proportion is an equation in which two ratios are set equal to each other. For example, if there is 1 boy and 3 girls you could write the ratio as: 1 : 3 (for every one boy there are 3 girl.
It has been reported that 8,475 persons attended a political event in South America.
The 12 nations and 3 territories of South America were equally
represented.
The proportion of attendees from each nation to the total number of
countries indicates the number of representatives who attended.
How many representatives there are is =
total number of attendees / total number of participating nations
8,475 / 12 = the number of representatives
There are 706.25 x 707 representations.
Consequently, 707 delegates from each nation attended political conferences.
To learn more about Ratios visit:
brainly.com/question/1504221
#SPJ4
Find the average temperature on that part of the plane \( 3 x+5 y+z=9=8 \) over the square \( |x| \leq 1,|y| \leq 1 \), where the temperature is given by \( T(x, y, z)=e^{-z} \).
Answers
The region is small, we assume that the temperature does not vary significantly over the region.
The overall average temperature over the region by taking the average of these four average temperatures:
\(\[\text{Average temperature}\) = \(\frac{\text{Average temperature}_1 + \text{Average temperature}_2 + \text{Average temperature}_3 + \text{Average temperature}_4}{4}\]\)
To find the average temperature over the given region, we need to calculate the integral of the temperature function \(\(T(x, y, z) = e^{-z}\)\) over the square region \(\(|x| \leq 1\) and \(|y| \leq 1\)\), and then divide it by the area of the region.
Let's begin by finding the limits of integration for (x) and (y). We are given that \(\(|x| \leq 1\) and \(|y| \leq 1\)\), which means the region is a square with side length 2 centered at the origin.
Next, we'll find the limits of integration for (z) by solving the equation of the plane for (z):
\(\[3x + 5y + z = 9 \implies z = 9 - 3x - 5y\]\)
Now, we can set up the integral:
\(\[I = \iint\limits_R e^{-z} \,dx\,dy\]\)
where (R) represents the region \(\(|x| \leq 1\) and \(|y| \leq 1\)\).
To evaluate this integral, we need to change the variables from (x) and (y) to new variables that correspond to the region (R). We'll use the transformation:
\(\[u = 3x + 5y \quad \text{and} \quad v = 9 - 3x - 5y\]\)
Let's find the Jacobian of this transformation:
\(\[\frac{\partial(u, v)}{\partial(x, y)} = \begin{vmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{vmatrix} = \begin{vmatrix} 3 & 5 \\ -3 & -5 \end{vmatrix} = -3 \cdot (-5) - 5 \cdot (-3) = -15 + 15 = 0\]\)
The Jacobian is zero, indicating that the transformation is degenerate. This means the variables (u) and (v) are not independent, and we cannot use this transformation.
Therefore, we need to find another way to evaluate the integral. Since the region (R) is small and simple, we can approximate the average temperature by evaluating the temperature function at a few points in the region and taking their average.
Let's divide the region into four smaller squares with side length 1 centered at the origin: ((-1, -1)), ((-1, 1)), ((1, -1)), and ((1, 1)). We'll evaluate the temperature function at the center of each square and take their average.
1. For the square centered at ((-1, -1)), the temperature is
\(\(T(-1, -1, z) = e^{-z}\).\)
To find the average temperature over this square, we integrate the temperature function over the range of \(z\) values:
\(\[\text{Average temperature} = \frac{1}{1 \times 1} \int\limits{-\infty}^{\infty} e^{-z} \,dz\]\)
Note that we integrate over the entire range of \(z\) because there are no restrictions on (z) for this square.
2. For the square centered at ((-1, 1)), we follow the same process and find the average temperature:
\(\[\text{Average temperature}_2 = \frac{1}{1 \times 1} \int\limits_{-\infty}^{\infty} e^{-z} \,dz\]\)
3. For the square centered at ((1, -1)), we find the average temperature:
Average temperature = \(\frac{1}{1 \times 1} \int\limits{-\infty}^{\infty} e^{-z} \,dz\]\)
4. For the square centered at ((1, 1)), we find the average temperature:
\(\[\text{Average temperature}4 = \frac{1}{1 \times 1} \int\limits{-\infty}^{\infty} e^{-z} \,dz\]\)
Finally, we can calculate the overall average temperature over the region by taking the average of these four average temperatures:
Average temperature = \(\frac{\text{Average temperature}_1 + \text{Average temperature}_2 + \text{Average temperature}_3 + \text{Average temperature}_4}{4}\]\)
Note that since the region is small, we assume that the temperature does not vary significantly over the region.
To know more about length click-
https://brainly.com/question/24571594
#SPJ11
If we take a simple random sample of size n=500 from a population of size 5,000,000, the variability of our estimate will be (a) much less than the variability for a sample of size n=500 from a population of size 50,000,000 . (b) slightly less than the variability for a sample of size n=500 from a population of size 50,000,000 . (c) about the same as the variability for a sample of size n=500 from a population of size 50,000,000 . (d) slightly greater than the variability for a sample of size n=500 from a population of size 50,000,000 . (e) much greater than the variability for a sample of size n=500 from a population of size 50,000,000 .
Answers
If we take a simple random sample of size n=500 from a population of size 5,000,000, the variability of our estimate will be (c) about the same as the variability for a sample size n=500 from a population of size 50,000,000.
The variability of an estimate primarily depends on the sample size (n) rather than the population size. Since both scenarios have a sample size of 500, the variability will be approximately the same.
The correct answer is (d) slightly greater than the variability for a sample size n = 500 from a population of size 50,000,000. This is because the larger the population size, the smaller the sampling variability. In other words, if we take a sample of the same size from a larger population, there will be more variability due to the increased number of potential outcomes. However, the difference in variability between a population size of 5,000,000 and 50,000,000 is not significant enough to make a substantial impact on the estimate.
Learn more about sample size:
brainly.com/question/30100088
#SPJ11
A study conducted by a TV station showed the number of televisions per household and the corresponding probabilities for each. Find the mean, variance and standard deviation. Chapter 5.3 Number of Televisions; X 1 2 3 4 P(X) 0.32 0.51 0.12 0.05
Answers
The mean number of televisions per household is approximately 1.93, the variance is approximately 0.7387, and the standard deviation is approximately 0.859.
To find the mean, variance, and standard deviation of the number of televisions per household, we use the formulas:
Mean = Σ(X * P(X))
Variance = Σ[(X - Mean)^2 * P(X)]
Standard deviation = sqrt(Variance)
Using the given probabilities, we can calculate the mean as follows:
Mean = (10.32) + (20.51) + (30.12) + (40.05) = 1.93
To calculate the variance, we first need to calculate the deviations from the mean:
1 - 1.93 = -0.93
2 - 1.93 = 0.07
3 - 1.93 = 1.07
4 - 1.93 = 2.07
Using these deviations and the given probabilities, we can calculate the variance as follows:
Variance = (-0.93^2 * 0.32) + (0.07^2 * 0.51) + (1.07^2 * 0.12) + (2.07^2 * 0.05) = 0.7387
Finally, we can calculate the standard deviation as the square root of the variance:
Standard deviation = sqrt(0.7387) = 0.859
Visit here to learn more about standard deviation:
brainly.com/question/24298037
#SPJ11
Carla and Ben earn commission every time they sell soemthing. Carla sold 3 suits and 1 pair of shoes, and earned 47$ in commission. Ben sold 7 suits and 2 pairs of shoes, and earned 107$ in commision. how much commission do they get from selling suits, and how much do they get from selling shoes
Answers
Answer:
$13
Step-by-step explanation:
Please tell me if i'm wrong.
you are treating a 50-year-old man that was involved in a fire. he suffered 25% 2nd-3rd degree burns to the anterior chest, neck and face. he has singed nasal hairs, and you identify stridor on your primary survey. pulse oximetry is 88% on a 100% non-rebreather mask. a burn center is 45 miles away. the next most appropriate step prior to transfer is:
Answers
A 100% non-rebreather mask has a pulse oximetry reading of 88%. There is a burn centre 45 miles distant. the best course of action to do after transferring a serious burn side.
A 50-year-old man who was injured in a fire is being treated by you. He sustained 25% 2nd–3rd degree burns to his face, neck, and anterior chest. He has burned nasal hairs, and your initial survey reveals stridor.
Any damage that exceeds 10% in size should be treated in a similar manner, although significant burns are classified as those that encompass 25% or more of the total body surface area. Rapid evaluation is essential. Any blaze can be managed using the general strategy for a significant burn. The most crucial things are to take a thorough history.
Learn more about burn Visit: brainly.com/question/14033152
#SPJ4
Which type of parent function is f(x) = 1/x?
Answers
Answer:
Rational Function
Step-by-step explanation:
A rational function is the ratio of two polynomials. Here, our polynomials are "1" and "x", hence, the name "Rational Function".
which expression is equivalent to this?

Answers
Answer:
45x^-10 or 45/x^10
Step-by-step explanation:
(3x^-4)^2 = 9x^-8
(9x^-8)*(5x^-2) = 45x10^-10
I don't see this answer in the options, but am wondering if the second one, 45/x10 is mistyped and is meant to be 45/x^10, which would be correct.
worth 14 points please help I need a expert
Write an equation to represent the angle?
What is the value of x?

Answers
Answer:
x=13
Step-by-step explanation:
we can guess that the three angles are a linear pair and equal 180
in this case we can start writing a equation
x+105+62=180
now we can subtract both whole numbers from 180 but that takes longer, so we will combine the whole numbers on the left side.
x+167=180
now we can go ahead and subtract 167 from both sides. by doing so, it isolates the x and gives you your answer
180-167=13
so... x=13
Please triple check

Answers
Answer: The answer should be \(\frac{1}{6}\) because that is the probability of that spinner
Step-by-step explanation:
why is it impossible to bisect a line?
Answers
Answer:
because a line tends to an infinite point and if the line is divided into two, you will not have equal parts
A circle is graphed on a coordinate grid and then reflected across the y-axis. If the center of the original circle was located at (x , y), which ordered pair represents the center of the new circle after the transformation?
A(-x,y)
B(-x,-y)
C(x,y)
D(x,-y)
Answers
The required ordered pair represents the center of the new circle after the transformation is (-x,y). Option A is correct.
What is the transformation of geometry over the coordinate plane?Transform the shapes on a coordinate plane by rotating, reflecting, or translating them.
Here,
If a circle is reflected across the y-axis, its center, which was originally located at (x, y), will move to a new location that is the same distance from the y-axis but on the opposite side. Since the y-coordinate does not change during a reflection across the y-axis, the y-coordinate of the new center will remain the same as the original, which is y.
However, the x-coordinate will be negated, since the reflection across the y-axis involves flipping points to the opposite side of the y-axis. Therefore, the center of the new circle will have the coordinates (-x, y).
So the answer is A) (-x, y).
Learn more about transformation here:
brainly.com/question/18065245
#SPJ9
An alloy contains 13. 5 gms of copper and 4. 5 gms of zinc. Find the ratio by mass of copper to zinc in the alloy
Answers
The ratio by mass of copper to zinc in the alloy is 3:1.
To find the ratio by mass of copper to zinc in the alloy, we need to first calculate the total mass of the alloy. We can do this by adding the mass of copper and zinc:
Total mass of alloy = 13.5 g + 4.5 g = 18 g
Now we can find the ratio of copper to zinc by dividing the mass of copper by the mass of zinc:
Ratio of copper to zinc = 13.5 g / 4.5 g = 3:1
Therefore, the ratio by mass of copper to zinc in the alloy is 3:1.
Learn more about mass here
https://brainly.com/question/86444
#SPJ11
4. Show that the matrix [XX-X'Z(ZZ)-¹Z'X). where both the x & matrix X and the x matrix Z. have full column rank and m2, is positive definite. Discuss the implications of this result in econometrics.
Answers
To show that the matrix A = [XX - X'Z(ZZ)^(-1)Z'X] is positive definite, we need to demonstrate two properties: (1) A is symmetric, and (2) all eigenvalues of A are positive.
Symmetry: To show that A is symmetric, we need to prove that A' = A, where A' represents the transpose of A. Taking the transpose of A: A' = [XX - X'Z(ZZ)^(-1)Z'X]'. Using the properties of matrix transpose, we have:
A' = (XX)' - [X'Z(ZZ)^(-1)Z'X]'. The transpose of a sum of matrices is equal to the sum of their transposes, and the transpose of a product of matrices is equal to the product of their transposes in reverse order. Applying these properties, we get: A' = X'X - (X'Z(ZZ)^(-1)Z'X)'. The transpose of a transpose is equal to the original matrix, so: A' = X'X - X'Z(ZZ)^(-1)Z'X. Comparing this with the original matrix A, we can see that A' = A, which confirms that A is symmetric. Positive eigenvalues: To show that all eigenvalues of A are positive, we need to demonstrate that for any non-zero vector v, v'Av > 0, where v' represents the transpose of v. Considering the expression v'Av: v'Av = v'[XX - X'Z(ZZ)^(-1)Z'X]v
Expanding the expression using matrix multiplication : v'Av = v'X'Xv - v'X'Z(ZZ)^(-1)Z'Xv. Since X and Z have full column rank, X'X and ZZ' are positive definite matrices. Additionally, (ZZ)^(-1) is also positive definite. Thus, we can conclude that the second term in the expression, v'X'Z(ZZ)^(-1)Z'Xv, is positive definite.Therefore, v'Av = v'X'Xv - v'X'Z(ZZ)^(-1)Z'Xv > 0 for any non-zero vector v. Implications in econometrics: In econometrics, positive definiteness of a matrix has important implications. In particular, the positive definiteness of the matrix [XX - X'Z(ZZ)^(-1)Z'X] guarantees that it is invertible and plays a crucial role in statistical inference.
When conducting econometric analysis, this positive definiteness implies that the estimator associated with X and Z is consistent, efficient, and unbiased. It ensures that the estimated coefficients and their standard errors are well-defined and meaningful in econometric models. Furthermore, positive definiteness of the matrix helps in verifying the assumptions of econometric models, such as the assumption of non-multicollinearity among the regressors. It also ensures that the estimators are stable and robust to perturbations in the data. Overall, the positive definiteness of the matrix [XX - X'Z(ZZ)^(-1)Z'X] provides theoretical and practical foundations for reliable and valid statistical inference in econometrics.
To learn more about eigenvalues click here: brainly.com/question/29861415
#SPJ11
the skills inWhat is the volume of the following figure?Front viewBack viewiş 1 cubic unitcubic unitsReport a problem

Answers
Given that each cube represents 1 cubic units, we need to count how many cubes are in the figure.
From the front view, we count 2 cubes.
From the back view, we count 5 cubes.
There are 5 + 2 = 7 cubes in total, so the volume of the figure is 7 cubic units.
when a has linearly independent columns and a = qr is a qr factorization, then the columns of q form an orthonormal basis for the column space of a.
Answers
The given statement exists true. A matrix is broken down into orthogonal (Q) and upper triangular (R) matrices in a process known as QR decomposition (factorization).
What is meant by QR factorization?A matrix can be expressed as the union of two distinct matrices, Q and R, using the QR matrix decomposition. R is a square upper/right triangular matrix and Q is an orthogonal matrix. R is also invertible because it is square and doesn't have zeros in its diagonal entries.
A matrix is broken down into orthogonal (Q) and upper triangular (R) matrices in a process known as QR decomposition (factorization). Finding eigenvalues and solving linear least squares problems both use QR factorization.
A = QR. Be aware that the QR-factorization of a rectangular matrix A is sometimes understood with Q square and R rectangular rather than Q rectangular and R square, as with the MATLAB command qr.
To learn more about QR factorization refer to:
https://brainly.com/question/22767840
#SPJ4
Please solve this question!!

Answers
Answer: (i) 1/221 (ii) 11/221 (iii) 95/663 (iv) 1/663
Step-by-step explanation:
(i) A deck of cards contains 4 Kings out of 52 total cards
1st draw: 4 Kings out of 52 total cards → 4/52 = 1/13
2nd draw: 3 remaining Kings out of 51 total remaining cards → 3/51 = 1/17
1st Draw 2nd Draw Outcome Probability
King: P(K) = 1/13 King: P(K₂/K₁) = 1/17 King, King (1/13) x (1/17) = 1/221
*************************************************************************************************
(ii) A deck of cards contains 4 Jacks, 4 Queens, & 4 Kings out of 52 total cards
1st draw: 12 Face cards out of 52 total cards → 12/52 = 3/13
2nd draw: 11 remaining Face cards out of 51 total remaining cards → 11/51
1st Draw 2nd Draw Outcome Probability
Face: P(F) = 3/13 Face: P(F₂/F₁) = 11/51 Face,Face (3/13) x (11/51) = 11/221
*************************************************************************************************
(iiI) A deck of cards contains 26 black cards out of 52 total cards but there are 2 black Jacks, 2 black Queens, and 2 black Kings.
1st draw: 20 Black (not Face) cards out of 52 total cards → 20/52 = 5/13
2nd draw: 19 remaining Black (not Face) cards out of 51 total remaining cards → 19/51
1st Draw 2nd Draw Outcome Probability
Black: P(B~) = 5/13 Black: P(B~₂/B~₁) = 19/51 B~,B~ (5/13) x (19/51) = 95/663
*************************************************************************************************
(ii) A deck of cards contains 4 Aces out of 52 total cards
1st draw: 4 Aces out of 52 total cards → 4/52 = 1/13
2nd draw: 1 Queen of Hearts out of 51 total remaining cards → 1/51
1st Draw 2nd Draw Outcome Probability
Ace: P(A) = 1/13 Qh: P(Qh₂/A₁) = 1/51 Ace,Queen(h) (1/13) x (1/51) = 1/663
8(x-10)=-88
Show work
Check
Answers
Answer:
x = - 1
Step-by-step explanation:
Given:
8(x-10)=-88
Solve:
8(x-10)=-88
Using the distributive property.
How to use distributive property:
Multiply the outside number by the inside parenthesis numbers.
Like this;
8x - 80 = -88
Now add 80 to both sides:
8x - 80+80 = -88+80
8x = -8
Divide both sides by 8:
x = -1
Check:
We can substitute x which is -1 into the equation;
8(-1-10)
8*((-1)-10)
= -88
Hence, x = -1
RevyBreeze
can you help look at the photo above

Answers
Answer:
A
Step-by-step explanation:
3-3 is 0
0 is greater than -7
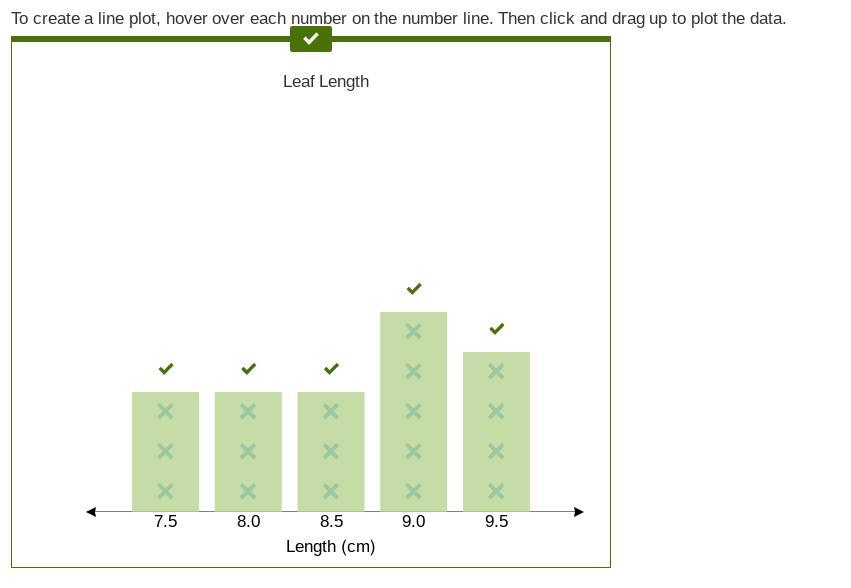
This list gives the lengths of different leaves in centimeters. 7.5, 9.5, 9.0, 8.0, 7.5, 8.5, 7.5, 8.5, 9.5, 8.5, 9.0, 9.5, 8.0, 9.5, 8.0, 9.0, 9.0, 9.0 Create a line plot to display the data. To create a line plot, hover over each number on the number line. Then click and drag up to plot the data.
Answers
These are the answers! Let me know if you need the rest of the answers on the assignment.
Which of the following is a counterexample to the given statement?
The name of every month ends in the letter y.
a. January
b. July
C February
d. December
Answers
The name of every month ends in the letter y is the given statement. February is a counterexample to this statement. This is because February does not end with the letter 'y'. So the right option is (c) February.
What is a counterexample?
In mathematics, a counterexample is an example that opposes or disproves a statement, proposition, or theorem. It is a scenario, an instance, or an example that goes against the given statement.
Therefore, a counterexample demonstrates that the given statement is false or invalid.In this case, the statement is: "The name of every month ends in the letter y." We have to find which of the months listed does not end in "y."February is the only month in the options listed that does not end in the letter "y."
Thus, it is a counterexample to the given statement. Therefore, the correct option is C, February.
For more questions on: counterexample
https://brainly.com/question/29197877
#SPJ8
Find the area of the figure.BRAINLEST if right

Answers
Answer:
41 ft² is the answer thank you
Answer:
the answer is 53 ft
Step-by-step explanation:
fist take the 3*3 square = 9
then the 4*11= 44(11 because I ssume the 8 ft does not account for the 3ft of the box)(if it is 8 ft then the answer is 41 ft^2 overall)
44+9= 53
Find h, the height of the
triangle.
53 units
56 units
Answers
A cone has a volume of 100x cubic centimeters and a height of 12 centimeters. What is the radius of the base of the
cone in centimeters?
A. 10 cm
B. 5 cm
C. 25 cm
D. Not here
Answers
Is g(x) a function?? Please if anyone could answer I’m trying to get my grades up

Answers
Answer:
Yes this is a function.
Step-by-step explanation:
You can tell this because there isnt any repeating x values. If there was ever a vertical (straight up and down) line then it isn't a funciton.
Alexandra places a 12 m long ladder against a tree, with the base of the ladder 7 m away from the base of the tree. Using Pythagoras' theorem, calculate how far up the tree the ladder reaches. Give your answer in metres (m) to 1 d.p.
Answers
The value of distance up the tree the ladder reaches is, 9.7 meters
We have to given that;
Alexandra places a 12 m long ladder against a tree, with the base of the ladder 7 m away from the base of the tree.
Now, Let distance up the tree the ladder reaches is, x
Hence, By Pythagoras theorem we get;
12² = 7² + x²
144 = 49 + x²
144 - 49 = x²
x² = 95
x = √95
x = 9.7 meters
Thus, The value of distance up the tree the ladder reaches is, 9.7 meters
Learn more about the Pythagoras theorem visit:
https://brainly.com/question/343682
#SPJ1
The area covered by a topic lie plant triples every year. By what factors does the are covered by the plant increase every month?
Answers
Answer:
16.67%
Step-by-step explanation:
If area triples every year :
This means that :
With an initial area of 10;
Area at the end of the year = 3 * 10 = 30
Percentage increase per year :
(30 - 10) / 10 * 100%
(20 / 10) * 100%
2 * 100%
= 200% per year
Therefore, monthly increase %
Yearly % increase ÷ number of months in a year
200% ÷ 12
= 16.666666%
= 16.67%
can someone pls answer this fast and explain your answer. I WILL MARK YOU BRAINLIST!



Answers
Answer:
#1
Use ratios to solve similar triangles
x/5 = 30/8x = 5*30/8x = 18.75Option A#2
The included angles are
∠PQT ≅ ∠RQS as vertical anglesOption B#3
AD = DB, AE = EC D is midpoint of AB, E is midpoint of ACDE is midsegment and midsegment is half of the parallel side:DE = 1/2 BCOption C
A 18.75
B vertical angles are congruent
30/8= 3.75
5• 3.75=18.75
Find the area of the region enclosed by one loop of the curve. r=7cos(3θ)
Answers
The area enclosed by one loop of the curve is found to be 0.
The equation of the curve is r = 7 cos (3θ).
To find the area of the region enclosed by one loop of the curve, we need to determine the limits of integration. This is accomplished by calculating the points of intersection of the curve with itself, which correspond to θ values.
The curve intersects itself at θ = π/6 and θ = 5π/6.
We want to calculate the area of the region between these two points, so the limits of integration are π/6 and 5π/6.
We can use the formula for the area enclosed by a polar curve, which is given by the integral:
r/2 × [θ2 - θ1]
In this case,
r = 7 cos (3θ) and
θ1 = π/6,
θ2 = 5π/6.
Therefore, the area enclosed by one loop of the curve is:
r/2 × [θ2 - θ1]
= 7 cos (3θ)/2 × [5π/6 - π/6]
= 7 cos (3θ)/2 × π/3
= (7/2π) × cos (3θ) dθ,
integrated from π/6 to 5π/6.
This integral is a bit tricky to evaluate, but it can be done using integration by substitution.
First, we make the substitution u = 3θ, so that du/dθ = 3.
Then, we can write the integral as: (7/6π) ∫ cos u du, integrated from π/2 to (5π/2)
This integral evaluates to 0, so the area enclosed by one loop of the curve is 0.
Know more about the polar curve,
https://brainly.com/question/29197119
#SPJ11
This figure represents a design that is sewn onto a quilt square. The semicircles are a solid green fabric and the square is a floral fabric. The area of the solid green fabric is 8π square inches.
What percent of the design is floral fabric?
Use 3.14 for π. Round your answer to the nearest whole percent.
50 POINTS!!

Answers
The total percent of the design which is floral fabric made in the shape of quilt square is 13.73%.
What is area of square?Area of square is the square of its sides length. It can be given as,
\(A=a^2\)
Here, (a) is the length of the side of the square.
This figure represents a design that is sewn onto a quilt square. The semicircles are a solid green fabric and the square is a floral fabric.
The area of the solid green fabric is 8π square inches. There are total 8 semicircles made by the solid green fabric. Thus the area of the one semicircle is,
\(A=\dfrac{8\pi}{4}\\A=2\pi\)
The area of the semicircle is half of πr², where r is the radius of the circle. Therefore,
\(A=\dfrac{\pi r^2}{2}\\2\pi=\dfrac{\pi r^2}{2}\\4=r^2\\r=2\)
This radius of the semicircle is equal to the side of the square. Thus, the area of the side square made with floral fabric is,
\(A=2^2\\A=4\rm\; in^2\)
Thus, the percent floral fabric in the design is,
\(p=\dfrac{4}{8\pi+4}\times100\\p=\dfrac{4}{8\times3.14+4}\times100\\p=13.73\%\)
Thus the total percent of the design which is floral fabric made in the shape of quilt square is 13.73%.
Learn more about the area of square here;
https://brainly.com/question/1658516
It’s 39 bro I have no clue what the other guy is talking about
Step-by-step explanation: