Answers
Answer:
EL = AR
Explanation:
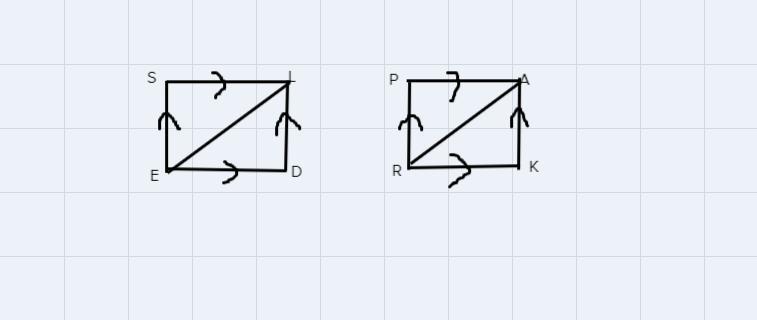
Find the diagram SLED and PARK below;
From both diagram, you can see that;
SE = PR
SL = PA
LD = AK
ED = RK
Also based on the diagonal EL = AR and SD = PK
Hence the correct option is EL = AR
Related Questions
if a₁=3 and aₙ=5aₙ-₁ then find the value of a₅
Answers
Answer:
The value of a₅ is 1875.
Step-by-step explanation:
Given:
a₁ = 3
aₙ = 5aₙ₋₁
To find the value of a₅, we can apply the recursive formula to compute each term successively:
Step 1: Compute a₂
a₂ = 5a₁ = 5(3) = 15
Step 2: Compute a₃
a₃ = 5a₂ = 5(15) = 75
Step 3: Compute a₄
a₄ = 5a₃ = 5(75) = 375
Step 4: Compute a₅
a₅ = 5a₄ = 5(375) = 1875
Suppose b, c R. Define T: P(R) → R2 by Tp=(3p(4) + 5p'(6)+bp(1)p(2), x3 p(x) dx + c sin p(0) Show that T is linear if and only if b = c = 0.
Answers
Therefore, additivity and homogeneity of T are satisfied, T is linear.
T must be linear for both b and c to be true. T is linear, hence additivity is true for every p, q, and P. (R). In order to make our computations as straightforward as feasible, it would be a good idea for us to use straightforward polynomials in P(R). p, q ∈ P(R), where p(x) = \(\frac{\pi }{2}\) and q(x) = \(\frac{\pi }{2}\) for all x ∈ R and so we have
T(p + q) =(3(p + q)(4) +5(p + q)'(6)+b(p + q)(1)(p + q)(2) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p + q)(x) d(x) + c sin((p + q)(0))
= (3(p(4)+q(4)) + 5(p'(6)+q'(6))+b(p(1)+q(1))(p(2)+q(2)) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p(x)+q(x))d(x)+ c sin(p(0)+q(0)))
= (3(\(\frac{\pi }{2}\) +\(\frac{\pi }{2}\))+5(0+0)+b(\(\frac{\pi }{2}\)+\(\frac{\pi }{2}\))(\(\frac{\pi }{2}\)+\(\frac{\pi }{2}\)), \(\int\limits^2_ {-1} \,\) \(x^{3}\)(\(\frac{\pi }{2}\)+\(\frac{\pi }{2}\))d(x)+c sin(\(\frac{\pi }{2}\)+\(\frac{\pi }{2}\)))
= (3(\(\pi\))+b\(\pi ^{2}\),\(\frac{15\pi }{4}\))
and
Tp + Tq = (3p(4) +5(p)'(6)+bp(1)(p)(2) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p)(x) d(x) + c sin((p)(0)) +(3(q)(4) +5(q)'(6)+b(q)(1)(q)(2) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(q)(x) d(x) +c sin(q(0)))
= (3(\(\frac{\pi }{2}\))+5(0)+b(\(\frac{\pi }{2}\))(\(\frac{\pi }{2}\)), \(\int\limits^2_ {-1} \,\) \(x^{3}\)(\(\frac{\pi }{2}\))d(x)+c sin(\(\frac{\pi }{2}\))) + (3(\(\frac{\pi }{2}\))+5(0)+b(\(\frac{\pi }{2}\))(\(\frac{\pi }{2}\)), \(\int\limits^2_ {-1} \,\) \(x^{3}\)(\(\frac{\pi }{2}\))d(x)+c sin(\(\frac{\pi }{2}\)))
=(3(\(\frac{\pi }{2}\))+\(\frac{\pi b}{4}\),\(\frac{\pi }{2}\) \(\int\limits^2_ {-1} \,\) \(x^{3}\)d(x) + c) +(3(\(\frac{\pi }{2}\))+\(\frac{\pi b}{4}\),\(\frac{\pi }{2}\) \(\int\limits^2_ {-1} \,\) \(x^{3}\)d(x) + c)
=(3\(\pi\)+ \(\frac{\pi b}{2}\),\(\frac{15\pi }{4}\)+2c)
Since T is linear, additivity of T holds and implies that we have
(3(\(\pi\))+b\(\pi ^{2}\),\(\frac{15\pi }{4}\)) = T(p+q)
=Tp+Tq
=(3\(\pi\)+ \(\frac{\pi b}{2}\),\(\frac{15\pi }{4}\)+2c)
from which we can equate the coordinates to obtain the equations 3π + πb/2= 3π +πb/2 and 15π/4 =15π/4+2c, which imply b = 0 and c = 0, respectively.
Backward direction: If b = 0 and c = 0, then T is linear. Suppose b = 0 and c = 0. Then the map T : R ^3 → R^2 becomes
Tp = (3p(4) +5(p)'(6) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p)(x) d(x) )
we need to prove that T is linear
• Additivity: For all p, q ∈ P(R), we have
T(p+q) = (3(p + q)(4) +5(p + q)'(6) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p + q)(x) d(x))
=(3(p(4)+q(4)) + 5(p'(6)+q'(6)) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p(x)+q(x))d(x))
= (3p(4) +5(p)'(6)+3q(4)+5q'(6) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p)(x) d(x) + \(\int\limits^2_ {-1} \,\) \(x^{3}\)q(x) d(x))
= (3p(4) +5(p)'(6) , \(\int\limits^2_ {-1} \,\) \(x^{3}\)(p)(x) d(x)) +(3(q)(4) +5(q)'(6), \(\int\limits^2_ {-1} \,\) \(x^{3}\)(q)(x) d(x))
=Tp+Tq
• Homogeneity: For all λ ∈ F and for all (x, y, z) ∈ R^3, we have
T(λp) = (3(λp)(4) + 5(λp)'(6), \(\int\limits^2_ {-1} \,\) \(x^{3}\)(λp)(x) d(x))
=(3λp(4) + 5λp'(6), \(\int\limits^2_ {-1} \,\) \(x^{3}\)λ(p)(x) d(x))
=(λ(3p(4) + 5p'(6)),λ \(\int\limits^2_ {-1} \,\) \(x^{3}\)p)(x) d(x))
=λ(3p(4) + 5p'(6), \(\int\limits^2_ {-1} \,\) \(x^{3}\)p)(x) d(x))
=λTp
Therefore, additivity and homogeneity of T are satisfied, T is linear.
To learn more about additivity:
https://brainly.com/question/20286983
#SPJ4
Marcus was showing how he solved a division problem with the area model below. His pen exploded ink on some of his work.
What is the divisor that is covered with ink on the left side of the model?
A. 100
B. 80
C. 56
D. 29

Answers
Answer:
C
Step-by-step explanation:
Graph makes no sense to me

Answers
Answer:
(a) 0
(b) 0
(c) 1
The function is not continous at x = 9
Step-by-step explanation:
To the left and right of the point x = 9, the graph would seem to continue at f(x) = 0, however on the exact point x = 9 there is a hole in the graph allowing it to be equal to 1. Due to the hole in the graph, it is not continuous
Apologies if this is wrong its been a bit since I did calculus
Irina ran 1/2 in 3 1/2 minutes. At that rate, how long would it take her to run 2 miles?
Answers
Answer:
Step-by-step explanation:
14 mins
this is because if we divide 2 but 1/2 you would get 4
since she can run 1/2 a mile in 3 1/2 mins
we should multiply the 3 1/2 buy 4
this would lead to the answer 14
fill in the mission numbers to make the fractions equivalent. 1/2 and /8= 4/12 and /60= 2/3 and /12= 4/4 and /8=
Answers
To make the fractions equivalent, we need to find the missing numerators that would make them equal. Let's fill in the missing numerators:
1/2 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
1/2 and 4/8
Now, the fractions are equivalent.
---
4/12 and __/60
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 5:
4/12 and 20/60
Now, the fractions are equivalent.
---
2/3 and __/12
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
2/3 and 8/12
Now, the fractions are equivalent.
---
4/4 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 2:
4/4 and 8/8
Now, the fractions are equivalent.
HURRY PLEASEE
WILL GIVE BRAINLEST

Answers
Answer:
A. x=8 B. x=25
Step-by-step explanation:
for a.
70/50=1.4
60*1.4=11x-4
84=11x-4
88=11x
x=8
for b.
72/27=2/3
64/(2/3)=-4+4x
96=-4+4x
100=4x
x=25
Multiply.
(2x+6)²
NEED ANSWER ASAPP
Answers
Answer:
4x² + 24x + 36
Step-by-step explanation:
(2x + 6)² = (2x + 6)(2x + 6) = 4x² + 12x + 12x + 36 = 4x² + 24x + 36
What is the solution to the equation?
4q + 4 = 20
Question 4 options:
q = 4
q = 6
q = 16
q = 24
Answers
Answer:
q = 4
Step-by-step explanation:
4q + 4 = 20
or, 4q = 20 - 4
or, q = 16/4
or, q = 4
2y = 4x - 12
Find the x and the y intercept of the line.
Answers
0 = 4x - 12
Adding 12 to both sides:
12 = 4x
Dividing both sides by 4:
3 = x
For Y:
2y = 4(0) - 12
2y = -12
Dividing both sides by 2:
y = -6
Therefore, the y-intercept of the line is y = -6.
The bank manager wants to show that the new system reduces typical customer waiting times to less than 6 minutes. One way to do this is to demonstrate that the mean of the population of all customer waiting times is less than 6. Letting this mean be µ, in this exercise we wish to investigate whether the sample of 107 waiting times provides evidence to support the claim that µ is less than 6.
For the sake of argument, we will begin by assuming that µ equals 6, and we will then attempt to use the sample to contradict this assumption in favor of the conclusion that µ is less than 6. Recall that the mean of the sample of 107 waiting times is = 5.27 and assume that σ, the standard deviation of the population of all customer waiting times, is known to be 2.23.
(a) Consider the population of all possible sample means obtained from random samples of 107 waiting times. What is the shape of this population of sample means? That is, what is the shape of the sampling distribution of ?
(b) Find the mean and standard deviation of the population of all possible sample means when we assume that µ equals 6. (Round your answer to 4 decimal places.)
(c) The sample mean that we have actually observed is = 5.27. Assuming that µ equals 6, find the probability of observing a sample mean that is less than or equal to = 5.27. (Round "z-value" to 2 decimals and final answer to 4 decimal places.)
(d) If µ equals 6, what percentage of all possible sample means are less than or equal to 5.27? What do you conclude about whether the new system has reduced the typical customer waiting time to less than 6 minutes? (Round your answer to 2 decimal places.)
Answers
The shape of the population sample means is large, the mean and standard deviation is 6 and 0.2155, the probability of sample mean is 0.37172 and it is conclude that mean is less than 6.
Given that sample of 107 waiting times provides evidence to support the claim that µ is less than 6 and for the waiting times mean is \(\bar{x}\)=5.27 and standard deviation is 2.23.
(a) It is observed that the sample size n=107, population mean μ=6, sample mean \(\bar{x}\)=5.27, and population standard deviation σ=2.23.
The Central Limit Theorem (CLT) states that for a large number of samples, the sample mean tends to approximate the standard value. Using this, it can be asserted that the sample mean follows an approximate normal distribution with μ and variance σ²/n. So, this data will follows a normal distribution because it is very large.
(b) The given mean of all samples is μ=6.
The standard error (SE) is same as the standard deviation of the sample mean. SE is computed as shown below:
SE=√(σ²/n)
SE=σ/√n
SE=2.23/√107
SE=0.2155
In notations,
\(\bar{x}\sim N(\mu=6,SE=0.2155)\)
(c) For a single mean (n=1), the z-score is given as follows:
\(\begin{aligned}z&=\frac{\bar{x}-\mu}{\sigma}\sim N(0,1)\\ &=\frac{\bar{x}-6}{2.23}\end{aligned}\)
Then, the probability less than or equal to 5.27 is computed as given below:
\(\begin{aligned}P(\bar{x}\leq 5.27)&=P\left(\frac{\bar{x}-6}{2.23}\leq \frac{5.27-6}{2.23}\right)\\ &=P(z\leq -0.3273)\\ &=P(z > 0.3273)\\ &=1-P(z \leq 0.3273)\end{aligned}\)
Using the normal table, it is found out that P(z≤0.3273)=0.6282
\(\begin{aligned}P(\bar{x}\leq 5.27)&=1-0.62828\\&=0.37172\end\)
d. If the population mean =6 and sample mean is 5.27 then there is 3.71% that sample mean is less than 5.27 hence we conclude that means is less than 6.
Hence, when the mean of the sample of 107 waiting times is = 5.27 and assume that σ, the standard deviation is known to be 2.23. the shape of the population sample means is large, the mean and standard deviation is 6 and 0.2155, the probability of sample mean is 0.37172 and it is conclude that mean is less than 6.
Learn more about the standard deviation from here brainly.com/question/16903717
#SPJ9
8(-8x – 6) = -6x - 22
solve for x
Answers
Answer:
x = - 13/29 OR x = - -0.44827586
Step-by-step explanation:
We use PEMDAS to evaluate the equation.
P stands for parenthesis. In this case we distribute the 8 to the equation in parenthesis.
8(-8x - 6)
-64x - 48 = -6x - 22 we will move the terms to their proportional sides
-64x + 6x = 22 + 48 (remember we do the opposite equation to move to the other side of the equals to sign)
-58x = 70 we divide both sides by -58 to isolate x
x = - 13/29 OR x = - -0.44827586
Answer: I got 3.18 repeating
Step-by-step explanation:
a. Find the slope of x^3+y^3-65xy=0 at the points (4,16) and (16,4).
b. At what point other than the origin does the curve have a horizontal tangent line?
c. Find the coordinates of the point other than the origin where the curve has a vertical tangent line.

Answers
a. The slope of the curve at the point (4,16) is approximately 1.165, and at the point (16,4) is approximately -0.496.
b. The curve has a horizontal tangent line at the points(0,0) and (3,27).
c. The curve has a vertical tangent lineat the points (0,0) and (65/2, (65/2)³).
How is this so?a. To find the slope of the curve given by the equation x³ + y³ - 65xy = 0 at the points (4,16) and (16,4),we can differentiate the equation implicitly with respect to x and solve for dy/dx.
Differentiating the equation with respect to x, we have -
3x² + 3y²(dy/dx) - 65y - 65x(dy/dx) = 0
To find the slope at a specific point, substitute the x and y coordinates into the equation and solve for dy/dx.
For the point (4,16) -
3(4)² + 3(16)²(dy/dx) - 65(16) - 65(4)(dy/dx) = 0
48 + 768(dy/dx) - 1040 - 260(dy/dx) = 0
508(dy/dx) = 592
(dy/dx) = 592/508
(dy/dx) ≈ 1.165
For the point (16,4) -
3(16)² + 3(4)²(dy/dx) - 65(4) - 65(16)(dy/dx) = 0
768 + 48(dy/dx) - 260 - 1040(dy/dx) = 0
(-992)(dy/dx) = 492
(dy/dx) = 492/(-992)
(dy/dx) ≈ -0.496
Thus, the slope of the curve at the point (4,16) isapproximately 1.165, and at the point (16,4) is approximately -0.496.
b. To find the point where the curve has a horizontal tangent line, we need to find the x-coordinate(s)where dy/dx equals zero.
This means the slope is zero and the tangent line is horizontal.
From the derivative we obtained earlier -
3x² + 3y²(dy/dx) - 65y - 65x(dy/dx) = 0
Setting dy/dx equal to zero -
3x² - 65y = 0
Substituting y = x³/65 into the equation -
3x² - 65(x³/65) = 0
3x² - x³ = 0
Factoring out an x² -
x²(3 - x) = 0
This equation has two solutions - x = 0 and x = 3.
hence, the curve has a horizontal tangent line at the points(0,0) and (3,27).
c. To find the point where the curve has a vertical tangent line, we need to find the x-coordinate(s) where the derivative is undefinedor approaches infinity.
From the derivative -
3x² + 3y²(dy/dx) - 65y - 65x(dy/dx) = 0
To find the vertical tangent line, dy/dx should be undefined or infinite. This occurs when the denominator of dy/dx is zero.
Setting the denominator equal to zero: -
65x = 65y
x = y
Substituting this condition back into the original equation -
x³ + x³ - 65x² = 0
2x³ - 65x² = 0
x²(2x - 65) = 0
This equation has two solutions - x = 0 and x = 65/2.
Therefore, the curve has a vertical tangent line at the points (0,0)
and(65/2, (65/2)³).
Learn more about slope:
https://brainly.com/question/3493733
#SPJ1
Nelson lands 4650 on 2% interest rate. He plans to pay this after 2 months. What will the total principal and interest payment be?
Answers
The total principal and interest payment that Nelson will have to pay after 2 months is $4665.50.
To calculate the total principal and interest payment, we need to determine the interest amount and add it to the principal.
First, let's find the interest amount:
Interest = Principal x Interest Rate x Time
Given:
Principal = $4650
Interest Rate = 2% per year
Time = 2 months
Since the interest rate is given on an annual basis, we need to convert the time from months to years. There are 12 months in a year, so 2 months is equivalent to 2/12 = 1/6 years.
Interest = $4650 x 0.02 x (1/6) = $15.50
Now, we can calculate the total principal and interest payment:
Total Payment = Principal + Interest
Total Payment = $4650 + $15.50 = $4665.50
For more such questions on principal visit:
https://brainly.com/question/25720319
#SPJ8
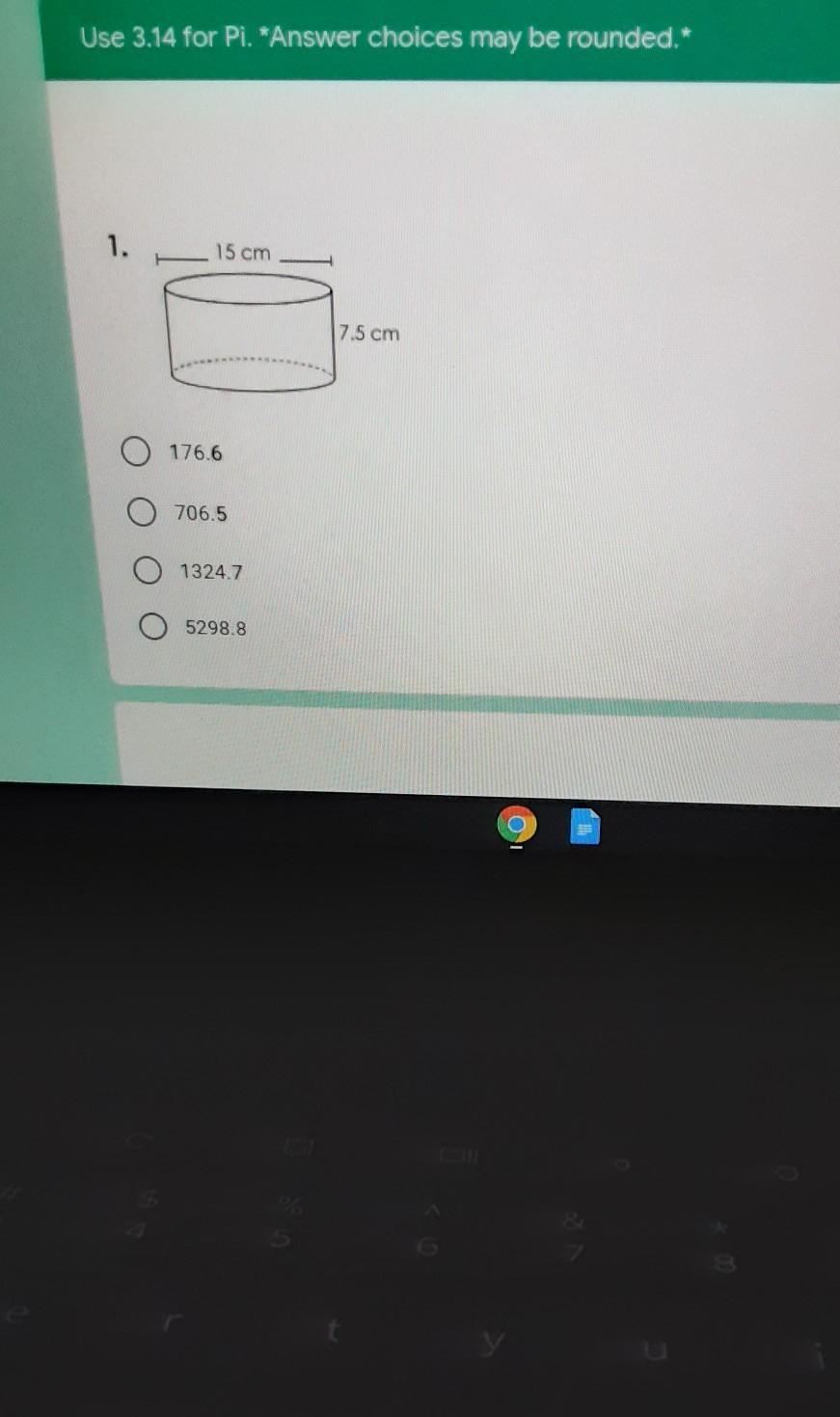
Use 3.14 for Pi. *Answer choices may be rounded.* 5 points 1. 15 cm 7.5 cm 176.6 706.5 1324.7 5298.8
Answers
Answer:
C. 1324.7 cm³
Step-by-step explanation:
Volume of cylinder = πr²h
π = 3.14
radius (r) = ½ of 15 = 7.5 cm
Height (h) = 7.5 cm
Plug in the values
Volume = 3.14*7.5²*7.5 = 1324.7 cm³
What is the length of Line segment A C? 3 ft 4 ft 18 ft 12 ft
Answers
Answer:
C 18 feet:D
Step-by-step explanation:
Answer:
The answer is C
Step-by-step explanation:
Hope you have a fantastic day, and do well on your test!!!!!!!!!!!!!!
Calculate curl(F and then apply Stokes' Theorem to compute the flux of curI(F) through the surface in the figure using line integral. The surface is a wedge-shaped box (bottom included, top excluded) with an outward-pointing normal. Assume that parameter a = 2. F= (x+yz - 16,x√(y^2 + 1)
(Express numbers in exact form: Use symbolic notation and fractions where needed ) curI(F) = ______ flux of curl(F) = _____
Answers
the flux of curI(F) through the surface area in the figure as with integral:
flux of curl(F) = x^2 + 4yz(2) + 2∫x√(y^2 + 1) dy - 32z + 2y^2z
First, we calculate the curl of F: curI(F) = (2z, -2x, 2y).
Next, we apply Stokes' Theorem to calculate the flux of curI(F) through the surface in the figure. We start by computing the line integral of F around the boundary of the surface. This is given by:
flux of curl(F) = 2 ∫ (x + 2yz) dx + 2 ∫ (x√(y^2 + 1))dy - 2 ∫ (16 - 2yz)dz
We can now evaluate this line integral by splitting it into a sum of integrals:
flux of curl(F) = 2 ∫ (x + 2yz) dx + 2 ∫ (x√(y^2 + 1))dy - 2 ∫ (16 - 2yz)dz
= 2∫x dx + 4∫yz dx + 2∫x√(y^2 + 1) dy - 32∫dz + 4∫yz dz
= 2x^2/2 + 4∫yz dx + 2∫x√(y^2 + 1) dy - 32z + 4yz^2/2
= x^2 + 4yz∫dx + 2∫x√(y^2 + 1) dy - 32z + 2y^2z
Finally, we can evaluate the flux of curI(F) through the surface in the figure as:
flux of curl(F) = x^2 + 4yz(2) + 2∫x√(y^2 + 1) dy - 32z + 2y^2z
Learn more about integral here
https://brainly.com/question/18125359
#SPJ4
Ad
Module 3 Mini Project
While there were about 3,000,000 people (about the population of Arkansas)
who visited the zoo last year, the number of people who visited in each
month was different. For example, people are more likely to visit the zoo in
July than they are in January. For that reason, the zoo raises its prices during
the months when there are a lot of visitors (peak season) and lowers its
prices during the months when there are not as many visitors (off season).
During peak season the zoo has about 1,800,000 visitors. Write an
expression to show how much money would be made during peak season
where p is the price of one peak season ticket.
The zoo wants to sell tickets in the off season for half of the price of tickets
in the peak season. Write an expression to show how much money would be
made during the off season where p is the price of one peak season ticket.
To break even the zoo needs to make at least how much money they spent
on the animals. Write and solve an inequality to find out how much the price
of one peak season ticket should be where p is the price of one peak season
ticket. How much should one off season ticket be?
Answers
Money made during peak season = 1,800,000 * p
1. Expression for money made during peak season:
During peak season, the zoo has about 1,800,000 visitors. To calculate the money made during peak season, we multiply the number of visitors by the price of one peak season ticket (p):
Money made during peak season = 1,800,000 * p
2. Expression for money made during the off season:
The zoo wants to sell tickets in the off season for half the price of tickets in the peak season. Therefore, the price of one off season ticket would be p/2. To calculate the money made during the off season, we multiply the number of visitors by the price of one off season ticket:
Money made during the off season = 1,200,000 * (p/2) = 600,000 * p
3. Inequality for breaking even:
To break even, the zoo needs to make at least as much money as they spent on the animals. Let's represent the amount spent on animals as A. The money made during peak season plus the money made during the off season should be greater than or equal to the amount spent on animals:
1,800,000 * p + 600,000 * (p/2) ≥ A
Simplifying the inequality:
3,600,000p + 300,000p ≥ 2A
3,900,000p ≥ 2A
Solving for p:
p ≥ (2A) / 3,900,000
This determines the minimum price of one peak season ticket to break even.
The price of one off season ticket would be half the price of one peak season ticket, so the off season ticket should be (p/2).
For more such questions on season, click on:
https://brainly.com/question/25000811
#SPJ8
The graph shows the distribution of the lengths (in seconds) of videos on a popular video-streaming site. The distribution is approximately Normal, with a mean of 264 seconds and a standard deviation of 75 seconds.
A graph titled Streaming Videos has length (seconds) on the x-axis, going from negative 36 to 564. The highest point of the curve is at 264.
What percentage of videos on the streaming site are between 264 and 489 seconds?
0.15%
49.85%
95%
99.7%
Answers
According to the properties of the standard normal distribution, approximately 99.7% of the values lie within three standard deviations of the mean. Therefore, the answer is 99.7%.
To determine the percentage of videos on the streaming site that are between 264 and 489 seconds, we need to calculate the area under the normal curve within that range. Since the distribution is approximately normal with a mean of 264 seconds and a standard deviation of 75 seconds, we can use the properties of the standard normal distribution to find the desired percentage.
First, we need to convert the values 264 and 489 to z-scores, which represent the number of standard deviations a particular value is away from the mean. The z-score formula is given by:
z = (x - μ) / σ
where x is the value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get:
z1 = (264 - 264) / 75 = 0
z2 = (489 - 264) / 75 = 3
Next, we can use a standard normal distribution table or a calculator to find the area under the curve between z = 0 and z = 3. The area represents the percentage of videos falling within that range. The answer is 99.7% .
For more such questions on normal distribution
https://brainly.com/question/4079902
#SPJ8
Each of 150 volunteers was assigned at random to one of five rooms where they were asked to taste and rate a glass of wine. In one of the rooms, no music was playing and a different style of music was playing in each of the other four rooms. The researchers concluded that cabernet sauvignon is perceived as being richer and more robust when bold music is played than when no music is heard.
Required:
a. Is the study described an observational study or an experiment?
b. Can a case be made for the researcher's conclusion that the music played was the cause for the higher rating? Explain.
Answers
Answer:
a. Experiment
b. yes
Step-by-step explanation:
The study being conducted in this scenario is an experiment because different groups are being created and both an independant variable and dependant variable are being introduced. This means that there is researcher involvement and therefore makes this an experiment and not an observational study.
Yes, a case can be made for such a claim. This is because the music being played is the dependent variable in each of the groups. Meaning that the only difference in each of the groups was the music. Therefore, any differences in the data gathered can be connected to the music.
Hi how are you today can you please help me with this question

Answers
$ 119.607
Explanation
we can easily solve this by using a rule of three
Step 1
Let
actual price(2020)=price of 2019 + 2%
so
actual price(2020)= 102 % and
price ( 2019)=100 %
let x represents the cost for 2019, so
\(\begin{gathered} \text{if} \\ 122\Rightarrow\text{ 102\%} \\ x\text{ }\Rightarrow\text{ 100 \%} \end{gathered}\)the proportion would be
\(\begin{gathered} \frac{122}{102\text{ \%}}=\frac{x}{100\text{ \% }} \\ \text{ Multiply both sides by 100 \%} \\ \frac{122}{102\text{ \%}}\cdot100=\frac{x}{100\text{ \% }}\cdot100 \\ 119.607=x \end{gathered}\)therefore, the cost in January of 2019 is
$ 119.607
I hope this helps you
Using any example of a 2 by 2 matrix;
Show that (A inverse) inverse = A; where A is a 2 by 2 matrix
Answers
The inverse of A is A^-1 (see picture), where A^-1 = (1/(determinant of A))*(adjoint of A). Note that the inverse of A only exists if ad - bc ≠ 0.
So, if ANY example of a 2 by 2 matrix is allowed… we use an example where a = 1, b = 2, c = -3, d = -5. The inverse matrix will have the terms -5, -2, 3, 1. (See photo)
To show that the inverse OF the inverse equals A, follow the same process. And.. yes, (A^-1)^-1 = A. We want to see the identity matrix 1, 0, 0, 1 since A*A^-1 = I (this is an uppercase i).
I’m on my phone so it’s harder to type. Refer to the picture to see my work:
I hope this helps!

I need help on question 27

Answers
A = \(\frac{1}{2}h(b_{1} +b_{2} )\)
If A = 136 when \(b_{1}\) = 7 and h = 16, find \(b_{2}\)
Givens:We are given the equation that we are working with:
A = \(\frac{1}{2}h(b_{1} +b_{2} )\)
We are given certain values that the variables, in this case, are equal to:
A = 136
\(b_{1}\) = 7
h = 16
Steps:Substitute the given variables in the given equation for the corresponding numbers:
A = \(\frac{1}{2}h(b_{1} +b_{2} )\)
136 = \(\frac{1}{2}\) * 16 (7 + \(b_{2}\))
We know all the values in the equation except \(b_{2}\). In order to find \(b_{2}\) we must isolate it on one side of the equation
136 = 8 (7 + \(b_{2}\))
\(\frac{136}{8}\) = \(\frac{8 (7 + b_{2}) }{8}\)
17 = 7 + \(b_{2}\)
17 - 7 = 7 - 7 + \(b_{2}\)
10 = \(b_{2}\)
Check:If \(b_{2}\) is equal to 10 then if we plug it back into the given equation both sides of the equation should equal each other. Remember to use PEMDAS
136 = \(\frac{1}{2}\) * 16 (7 + \(b_{2}\))
136 = \(\frac{1}{2}\) * 16 (7 + 10)
136 = \(\frac{1}{2}\) * 16 (17)
136 = 8 (17)
136 = 136
\(b_{2}\) = 10
Pls pls help it is due todayyy:)))

Answers
Answer:
a dilation is different from a translation because it enlarges an image or shrink them instead of moving them. it's also different from rotation since it doesn't rotate but enlarge or shrink. it's way far from reflection because it enlarges or shrinks.
Answer: A diliation is a non rigid transformation, whereas reflections, transitions and rotations are rigid transformations. This means that dilations do not preserve the size of the shape.
A team of four boys and five girls is to be chosen from a group of six boys and eight girls. How many different teams are possible?
Answers
Answer:
There are a total of 840 possible different teams
Step-by-step explanation:
Given
Number of boys = 6
Number of girls = 8
Required
How many ways can 4 boys and 5 girls be chosen
The keyword in the question is chosen;
This implies that, we're dealing with combination
And since there's no condition attached to the selection;
The boys can be chosen in \(^6C_4\) ways
The girls can be chosen in \(^8C_5\) ways
Hence;
\(Total\ Selection = ^6C_4 * ^8C_5\)
Using the combination formula;
\(^nCr = \frac{n!}{(n-r)!r!}\)
The expression becomes
\(Total\ Selection = \frac{6!}{(6-4)!4!} * \frac{8!}{(8-5)!5!}\)
\(Total\ Selection = \frac{6!}{2!4!} * \frac{8!}{3!5!}\)
\(Total\ Selection = \frac{6 * 5* 4!}{2!4!} * \frac{8 * 7 * 6 * 5!}{3!5!}\)
\(Total\ Selection = \frac{6 * 5}{2!} * \frac{8 * 7 * 6}{3!}\)
\(Total\ Selection = \frac{6 * 5}{2*1} * \frac{8 * 7 * 6}{3*2*1}\)
\(Total\ Selection = \frac{30}{2} * \frac{336}{6}\)
\(Total\ Selection =15 * 56\)
\(Total\ Selection =840\)
Hence, there are a total of 840 possible different teams
In △ABC, AB=5, BC=4, and AC=3. The triangle is translated left 2 units and up 6 units to △A′B′C′. What is the length of segment A′C′?
A′C′=6
cap A prime cap c prime is equal to 6
A′C′=3
cap A prime cap c prime is equal to 3
A′C′=4
cap A prime cap c prime is equal to 4
A′C′=2
Answers
Answer:
3
Step-by-step explanation:
The entire triangle shifts 2 to the left and up 6, the lengths of the sides remain the same, therefore:
AC = A'C' = 3
Can someone explain to me why I got this question wrong? The reasoning for my answer (2, 3) for the vertex is because in the setup for the equation f(x) = a( x - h ) + k, x is subtracted from h. If h was negative, it would be adding instead because it'd be a negative and a negative. So I know h is positive. Am I misunderstanding the question? Will give brainliest!

Answers
Kevin's error is that he incorrectly identified the vertex of the parabola as (3, 2) instead of (2, 3), which resulted to the parabola opens downward. The correct vertex is at (2, 3) and the parabola opens upward.
Correcting an Error in Identifying the Vertex and Direction of a Parabola.You are correct that the vertex of the parabola can be determined using the equation f(x) = a(x - h)² + k, where the vertex is at (h, k). In this case, we have f(x) = -(x-2)² + 3, so the vertex can be found by setting x - 2 = 0, which gives x = 2. Plugging this value into the equation,
we get f(2) = -(2-2)² + 3 = 3, so the vertex is at (2, 3).
However, your reasoning for why h is positive is not correct. The expression x - h represents the horizontal distance from the vertex to any point on the parabola. So if x is greater than h, then the expression x - h will be positive, and if x is less than h, then the expression x - h will be negative. In this case, the vertex is at (2, 3), so we have h = 2. This means that any point to the right of the vertex will have a positive value of x - h, while any point to the left of the vertex will have a negative value of x - h.
Therefore, the correct explanation of Kevin's error is that he incorrectly identified the vertex as (3, 2) instead of (2, 3), and as a result, he also incorrectly concluded that the parabola opens downward. In fact, the parabola opens upward because the coefficient of the x² term, -1, is negative.
To know more about the vertex and direction of a parabola,
visit:https://brainly.com/question/20209326
#SPJ1
Sarah's vegetable soup recipe uses 2
cups of vegetables to make one pot of soup. She wants to triple the recipe.
How many cups of vegetables does she need?
Answers
Answer:
No.of cups for one soup : 2 cups
No.of cup for 3 soups: 2×3
=6
So , 6 cups of vegetable
HOPE IT HELPS U :)
A system of equations is created by using the line represented by 2 x + 4 y = 0 and the line represented by the data in the table below.
x
y
–1
8
3
–4
5
–10
6
–13
What is the x-value of the solution to the system?
Answers
A specific X-value for the solution ,-4 is not equal to -3/2.
The x-value of the solution to the system of equations, we need to solve the given equation and the line represented by the data in the table. Let's begin by examining the first equation, 2x + 4y = 0.
We can rewrite this equation in terms of y:
4y = -2x
y = (-2/4)x
y = (-1/2)x
Now, let's use the data from the table to create a system of equations:
For the first data point (-1, 8):
y = (-1/2)x
8 = (-1/2)(-1)
8 = 1/2
Since 8 is not equal to 1/2, the first data point does not satisfy the equation.
For the second data point (3, -4):
y = (-1/2)x
-4 = (-1/2)(3)
-4 = -3/2
Again, -4 is not equal to -3/2, so the second data point does not satisfy the equation.
We can continue this process for the remaining data points, but from the information given, it seems that none of the data points satisfy the equation. Therefore, there is no solution to the system of equations.
To know more about X-value.
https://brainly.com/question/31177175
#SPJ11
what is the slope of the line that passes thru (7,-6) and (6,-6)
Answers
The slope of the straight line passing through the two given points is undefined which means the line is parallel to the y-axis.
Let us consider the two points A(x₁,y₁) and B(x₂,y₂) be the two points (7,-6) and (6,-6) on the cartesian coordinates.
Let the slope of the line joining A (7,-6) and B(6,-6) be m.
We know that the slope of a line is given by:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
Slope of the line
= (6-7) / (-6+6)
= -1 / 0
= undefined
Since the slope is undefined we can say that the straight line is parallel to the y axis.
we know that tan 90° = ∞
So any line parallel to this line will have the same slope as the y axis.
Hence the slope of the given line is undefined or infinity.
To learn more about slope visit:
https://brainly.com/question/11559942
#SPJ1
