if the median of a normal distribution curve is known, what can be said about the mean?
Answers
If the median of a normal distribution is known, it can be said that the mean of the distribution is also equal to the median. This is because the normal distribution is symmetric, with the median and mean at the center of the curve.
For a normal distribution, the mean and median are equal, so if the median is known, then the mean is also known. In a normal distribution, the median represents the point where exactly half of the data falls below and half falls above that point. Since the mean is also the point where the data balances out, meaning the sum of the values above the mean is equal to the sum of the values below the mean, it is also equal to the median. Therefore, if the median of a normal distribution curve is known, we can conclude that the mean is also equal to that value.
You can learn more about median at
https://brainly.com/question/16408033
#SPJ11
Related Questions
a farmer plans to enclose a rectangular pasture adjacent to a river (see figure). the pasture must contain 245,000 square meters in order to provide enough grass for the herd. no fencing is needed along the river. what dimensions will require the least amount of fencing?
Answers
X = 700 m and Y = 350 m will require the least amount of fencing.
Area of a rectangular field = length × breath = 245000 = XY
⇒ Y = 245000/X
Perimeter of a rectangular field = X + 2Y
⇒P = X+ 2Y
⇒P = X + 490000/X
⇒ X + 490000X⁻¹
⇒P [X] = X + 490000X⁻¹
⇒P'[X] = 1+[-490000X⁻²]
⇒0 = 1 - 490000/X²
⇒X²= 490000
⇒X = 700 unit
As XY = 245000 [ area of a rectangle ]
⇒700Y = 245000
⇒Y = 350 unit.
Hence , P is minimum [ fencing ] when X = 700 unit and Y = 350 unit.
To understand more about maxima and minima refer -
https://brainly.com/question/27958412
#SPJ4
find a unit vector normal to the surface cos(xy) = ez − 2 at (1, π, 0).
Answers
The given surface is \(\cos(xy) = e^z-2\). The unit vector normal to this surface at the point (1, π, 0) is\(\vec{n}=\langle 0, 0, 1\rangle\).
A vector with a magnitude of one is termed a unit vector. To determine a unit normal vector for the given surface, start by describing the surface as a function of form F(x, y, z). Next, calculate this function's gradient and then normalize the outcomes.
Consider the normal vector \(\vec{n}=\langle a, b, c\rangle\) to the plane ax + by + cz = d. Given \(\cos(xy) = e^z-2\) then, z = ln(2+cos(xy)).
At point (x₀,y₀,z₀), the equation for the tangent plane to z = f(x,y) is written as, \(z-z_0 = f_x(x_0,y_0)(x-x_0) + f_y(x_0,y_0)(y-y_0)\). The value of \(f_x\) and \(f_y\) are
\(f_x = \frac{-y \sin(xy)}{(2+\cos(xy))}\) and \(f_y =\frac{ -x \sin(xy) }{ (2+\cos(xy))}\).
At *x, y) = (1, π), the value of \(f_x\) and \(f_y\) is zero. Then, the equation of the tangent plane is given as z-0=0+0 ⇒ z=0.
Then, the resulting unit normal vector is \(\vec{n}=\langle 0, 0, 1\rangle\).
To know more about unit vectors:
https://brainly.com/question/25544738
#SPJ4
A2 Shape C is similar to shape D
9 cm
C
x cm
9.6 cm
Work out the value of x.
D
6 cm
T
10

Answers
Answer:
If Shape C is similar to Shape D, then we know that the ratio of corresponding side lengths is the same. In this case, we can set up the following proportion:
9 / 6 = x / 10
To solve for x, we can cross-multiply and simplify:
9 * 10 = 6 * x
90 = 6x
x = 15
Therefore, the value of x is 15 cm.
Answer:
The answer for x is approximately 5.6
Step-by-step explanation:
9/9.6=x/6
cross multiply
9.6x=9×6
9.6x=54
divide both sides by 9.6
9.6x/9.6=54/9.6
x=5.625
x≈5.6
Use the following boiling point curve of a mixture to answer questions 1-5.
T
e
Р
90
80+
(C) 60-
50 --
A
B
Time (min)
C
D
(T)
E
F
1. At least how many different substances make up the mixture? How do you know.
Answers
It can be inferred that there are at least 3 different substances in the mixture
What is boiling point ?
Boiling point is the temperature at which the vapor pressure of a liquid equals the atmospheric pressure above it, causing the liquid to change phase and become a gas (i.e., boil). It is a physical property of a substance that depends on factors such as intermolecular forces, molecular weight, and atmospheric pressure. The boiling point is often used to identify and characterize substances, as it can provide information about their purity and chemical composition.
According to the question:
Based on the boiling point curve, it can be inferred that there are at least 3 different substances in the mixture. This is because there are 3 distinct plateau regions (A, B, and C) where the temperature remains constant while the mixture boils, indicating that each plateau corresponds to a different substance in the mixture.
To know more about boiling point visit:
https://brainly.com/question/14771622
#SPJ1
a. yes, reflection across y=x
b. no
c. yes, rotation 180
d. yes, translation up 3 units

Answers
Answer:
A
filler filler filler
Can Someone help me because i can't do it........

Answers
Answer:
A and C
Step-by-step explanation:
the amount of sheeps + the amount of goats will equal at most 26
and
there are no more than 14 sheeps so the amount of sheeps in less than 14
PLEASE HELP ME!!! THE RIGHT ANSWER WILL GET THE BRAINIEST!

Answers
Answer:
\(\sf D) \quad s=8 \frac{1}{4}t\)
Step-by-step explanation:
t = time (in hours) → this is the independent variables = total area cleaned (in square feet) → this is the dependent variable (as the number of square feet cleaned depends on the number of hours worked)Therefore, if the rate of cleaning is 8 1/4 square feet per hour, the relationship between s and t is:
\(\sf s=8 \frac{1}{4}t\)
please help with my math
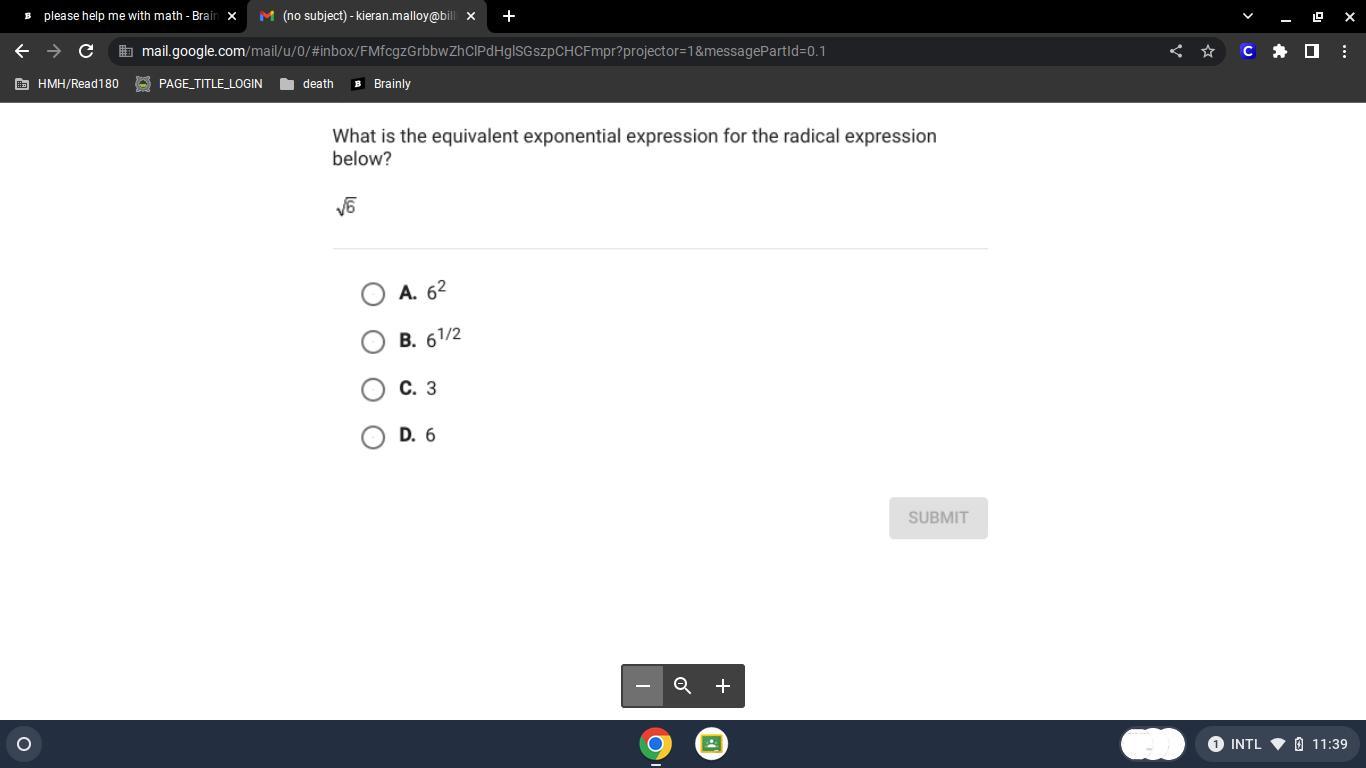
Answers
Answer:
B.) \(6^{\frac{1}{2}}\)
Step-by-step explanation:
Use the exponent rule that states \(a^{\frac{1}{m}}=\sqrt[m]{a}\). For this problem, let
a=6
m=2
So,
\(\sqrt6=6^{\frac{1}{2}}\)
2483 dividido 9 ayuda plis (help plis)
Answers
Answer: 275 \(\frac{8}{9}\)
Step-by-step explanation:

A public Interest group conducts a poll of 750 Randomly selected American households and finds that 67% of those surveyed have at least one dog.
a) construct and interpret a 90% confidence interval for the proportion of all American households who have at least one dog.
b) Explain what is meant by 90% confidence in this context
Answers
a. The 90% confidence interval for the proportion of all American households who have at least one dog is (0.636, 0.704). This means we can be 90% confident that the true proportion of all American households who have at least one dog lies within this range.
b. The 90% confidence means that if we were to repeat this poll many times with different samples of American households, we would expect 90% of the resulting confidence intervals to contain the true proportion of all American households who have at least one dog
a) To construct a 90% confidence interval for the proportion of all American households who have at least one dog, we can use the following formula:
CI = p ± zsqrt((p(1-p))/n)
where:
CI is the confidence interval
p is the sample proportion (67% or 0.67 in decimal form)
z is the z-score corresponding to the level of confidence (90% or 1.645 for a one-tailed test)
n is the sample size (750)
Plugging in the values, we get:
CI = 0.67 ± 1.645sqrt((0.67(1-0.67))/750)
CI = 0.67 ± 0.034
Therefore, the 90% confidence interval for the proportion of all American households who have at least one dog is (0.636, 0.704). This means we can be 90% confident that the true proportion of all American households who have at least one dog lies within this range.
b) In this context, 90% confidence means that if we were to repeat this poll many times with different samples of American households, we would expect 90% of the resulting confidence intervals to contain the true proportion of all American households who have at least one dog.
In other words, we can be reasonably sure that our sample proportion of 67% is a good estimate of the true proportion, with a margin of error of about 3.4 percentage points, based on the sample size and the level of confidence we have chosen.
Learn more about confidence interval at https://brainly.com/question/23411442
#SPJ11
A deposit of $10,000 is made in a trust fund that pays 3.8% interest, compounbed quarterly. It is specified that the balance will be given to Abudu Charity after the money has earned interest for 40years. How much will the charity receive?
Answers
9514 1404 393
Answer:
$45,395.39
Step-by-step explanation:
The formula for an amount earning compound interest is ...
A = P(1 +r/n)^(nt)
where principal P is invested at annual rate r compounded n times per year for t years.
Using the given numbers, we have ...
A = $10,000(1 +0.038/4)^(4·40) ≈ $45,395.39
The charity will receive $45,395.39.
Does this shape belong in a group of shapes that have more than one
perpendicular sides?
Use the drop-down menus to explain your answer.
Answers
Yes, this shape belong in a group of shapes that have more than one perpendicular sides because its sides meet at a right angle.
What are perpendicular lines?In Mathematics and Geometry, perpendicular lines can be defined as two (2) lines that intersect or meet each other at an angle of 90° (right angles) as shown in the image (see attachment) attached below.
However, it should be noted that it is not all intersecting lines that are perpendicular to each other because the lines may intersect at different angles other than 90 degrees (90°).
By critically observing the geometric shape, we can reasonably infer and logically deduce that it has more than one perpendicular sides.
Read more on perpendicular line here: https://brainly.com/question/28602079
#SPJ1

Fernando purchased 1 pound of dried cranberries and 4 pounds of almonds to make a trail mix. Cranberries cost $4 per pound and almonds cost $5 per pound. What is the price per pound of the trail mix? $
Answers
Answer:
$24
Step-by-step explanation:
Cranberries needed: 1 pound
Cost of 1 pound = $4
Almonds needed: 4 pound
Cost of 1 pound = $5
4 x 5 = $20
20 + 4 = $24
Answer:
4.80
Step-by-step explanation:
The function f is continuous on the interval (0,9) and is twice differentiable except at x = 6, where the derivatives do not exist (DNE). Information about the first and second derivatives of f for some values of x in the interval (0,9) is given in the table above. Which of the following statements could be false?

Answers
Answer:
The statement that could be false is;
(C) The function has a relative minimum at x = 6
Step-by-step explanation:
The given parameters are;
The function is continuous in the interval 0 ≤ x ≤ 9
The function is not differentiable at x = 6
f prime (x) = Negative for 4 < x < 6, and positive for 6 < x < 8
Therefore, at x = 6, the function is vertical
The statement that could be false is that the function has a relative minimum at x = 6.
A continuous function f(x) does not have discontinuity at any point
The statement that could be false is (c). The function f has a relative minimum at x = 6.
The interval is given as:
Interval = (0,9)
From the question, we understand that the function is not differentiable at x = 6.
This means that the function may or may not have a relative minimum at x = 6.
Hence, the statement that could be false is (c).
Read more about continuous functions at:
https://brainly.com/question/21447009
Hey can somebody get this for me been stuck for five min

Answers
Answer:
3
Step-by-step explanation:
it might be a semicolon instead of a comma I guess
I believe it is 1 because you might needa put a comma there.
using properties of the unit circle give the domain and range of the six trigonometric functions
Answers
The domain of all six trigonometric functions is all real numbers, and the range of the sine and cosine functions is between -1 and 1, while the range of the tangent, cosecant, secant, and cotangent functions is all real numbers except for certain values where the denominator is equal to zero.
Using the properties of the unit circle, we can define the six trigonometric functions (sine, cosine, tangent, cosecant, secant, and cotangent) based on the coordinates of points on the unit circle.
The domain of all six trigonometric functions is the set of all real numbers, since the input angle can take any value in radians or degrees.
The range of the sine and cosine functions is the set of all real numbers between -1 and 1, inclusive. This is because the y-coordinate (sine) and x-coordinate (cosine) of any point on the unit circle can range from -1 to 1.
The range of the tangent, cosecant, secant, and cotangent functions is the set of all real numbers except for values where the denominator (sine, cosine) is equal to zero. For example, the range of the tangent function is all real numbers except for the values of x where cos(x) = 0, which occur at multiples of pi/2.
So, in summary, the domain of all six trigonometric functions is all real numbers, and the range of the sine and cosine functions is between -1 and 1, while the range of the tangent, cosecant, secant, and cotangent functions is all real numbers except for certain values where the denominator is equal to zero.
Using properties of the unit circle, the domain and range of the six trigonometric functions are as follows:
1. Sine (sin): Domain is all real numbers, Range is [-1, 1].
2. Cosine (cos): Domain is all real numbers, Range is [-1, 1].
3. Tangent (tan): Domain is all real numbers except odd multiples of π/2, Range is all real numbers.
4. Cosecant (csc): Domain is all real numbers except integer multiples of π, Range is (-∞, -1] and [1, ∞).
5. Secant (sec): Domain is all real numbers except odd multiples of π/2, Range is (-∞, -1] and [1, ∞).
6. Cotangent (cot): Domain is all real numbers except integer multiples of π, Range is all real numbers.
Learn more about integer at: brainly.com/question/15276410
#SPJ11
Please help no links please

Answers
Answer:
C
Step-by-step explanation:
The secant- tangent angle MLK is half the difference of the intercepted arcs, that is
\(\frac{1}{2}\) (KN - KM) = 70° ( multiply both sides by 2 to clear the fraction )
KN - KM = 140°
KN - 61° = 140° ( add 61° to both sides )
KN = 201° → C
Helpppp pls I’m desperate!

Answers
The desired values of a and b to conform the translation (x,y) -> (x+a, y-b) to the format of a reflection around line q preceded by a reflection across line p are a = 2x+2 and b = y.
How to get the valuesLine q is a vertical line of equation x = -1, and the reflection of any point (x, y) across it provides its mirror image on the other side. Thus, reflecting a point (x, y) across line q results in the point (-x-2, y).
Additionally, line p is a horizontal line of equation y = b. When a point (x,y) is reflected across this line, its mirror image appears on the opposite side. Therefore, reflecting a point (x, y) across line p yields the point (x, 2b-y).
Presently, we seek to ascertain whether these two reflections are equivalent to shifting a point (x,y) to another point (x+a, y-b). Consequently, let us experiment with an arbitrary point (x,y): when we reflect it across line q, then over line p, then shift it by (a,-b), we should end up at (x+a, y-b).
Applying this pathway to our chosen point (x,y) gives the resultant point of (-x-2, y); followed by (-x-2, 2b-y); and finally (-x-2+a, 2b-y-b). Hence, for the transformation (x,y) -> (x+a, y-b) to be equivalent to one reflection about line q trailed by a reflection about line p, the following equations must resolve simultaneously:
-x-2+a = x+a
2b-y-b = y-b
By solving these equations, it is revealed that the desired values of a and b to conform the translation (x,y) -> (x+a, y-b) to the format of a reflection around line q preceded by a reflection across line p are a = 2x+2 and b = y.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
On a bicycle trail, the city is painting arrows like the one shown below:
Upper pointing arrow with height of 15 and length of 13. Rectangular base of arrow has length of 11 and height of 12. All units are in centimeters.
Calculate the area of the arrow by decomposing it into rectangles and triangles. (4 points)
195 square centimeters
171 square centimeters
151.5 square centimeters
148.5 square centimeters

Answers
The Area of the composite figure = area of the rectangle + area of the triangle = 148.5 cm².
What is the Area of a Composite Figure?The figure formed by the arrow can be decomposed into a rectangle and a triangle.
The area of the composite figure = area of the rectangle + area of the triangle.
Find the area of the rectangle:
Length = 12 cm
Width = 11 cm
Area of the rectangle = (length)(width) = (12)(11)
Area of the rectangle = 132 cm²
Find the area of the triangle
Base = 11 cm
Height = 15 - 12 = 3 cm
Area of the triangle = 1/2(b)(h) = 1/2(11)(3)
Area of the triangle = 16.5 cm²
Area of the composite figure = area of the rectangle + area of the triangle = 132 + 16.5 = 148.5 cm².
Learn more about the area of composite figure on:
https://brainly.com/question/15981553
#SPJ1
The chi-square goodness-of-fit test for multinomial probabilities with 5 categories has degrees of freedom. Multiple Choice 4 5 6 3
Answers
The chi-square goodness-of-fit test for multinomial probabilities with 5 categories has degrees of freedom of 4. The degrees of freedom in this test are calculated as (number of categories - 1). Since we have 5 categories, the degrees of freedom would be (5 - 1) = 4.
In the chi-square goodness-of-fit test, degrees of freedom represent the number of independent pieces of information available for estimating the parameters of the distribution. In this case, with 5 categories, we have 4 degrees of freedom. Degrees of freedom help determine the critical values for the chi-square test statistic and play a crucial role in interpreting the results. By knowing the degrees of freedom, we can compare the calculated chi-square value to the critical value from the chi-square distribution table to determine whether to reject or fail to reject the null hypothesis.
know more about test statistic here:
https://brainly.com/question/31746962
#SPJ11
The length of a rectangle i 2cm greater than the width of the rectangle. The perimeter of the rectangle i 24cm
Answers
The length of the rectangle is 7 cm and the width is 5 cm.
Perimeter of a rectangle:The whole distance covered by the rectangle's borders or its sides is known as its perimeter. As we know the rectangle will have 4 sides then the perimeter of the rectangle will be equal to the total of its four sides. And the unit will be in meters, centimeters, inches, feet, etc.
The formula for the Perimeter of the rectangle is given by
Perimeter = 2( Length + Width )Here we have
The length of a rectangle is 2cm greater than the width of the rectangle
And perimeter of the rectangle = 24 cm
Let x be the width of the rectangle
From the given data,
Length of the rectangle = (x + 2) cm
As we know Perimeter of rectangle = 2(Length+width)
=> Perimeter of rectangle = 2(x+2 + x) = 2(2x +2)
From the given data,
Perimeter of rectangle = 24cm
=> 2(2x +2) = 24 cm
=> (2x +2) = 12 [ Divided by 2 into both sides ]
=> 2x = 12 - 2
=> 2x = 10
=> x = 5 [ divided by 2 into both sides ]
Length of rectangle, (x+2) = 5 + 2 = 7 cm
Therefore,
The length of the rectangle is 7 cm and the width is 5 cm.
Learn more about Perimeter of a rectangle at
https://brainly.com/question/29595517
#SPJ4
Express the confidence interval 0.039 < p < 0.479 in the form p± E. A. 0.22 ±0.5 B. 0.259 ±0.5 C. 0.259 ±0.44
D. 0.259 ±0.22
Answers
Answer:
Step-by-step explanation:
To express the confidence interval 0.039 < p < 0.479 in the form p ± E, we need to find the midpoint of the interval and half of the width.
The midpoint of the interval is the average of the lower and upper bounds:
Midpoint = (0.039 + 0.479) / 2 = 0.259
The width of the interval is the difference between the upper and lower bounds:
Width = 0.479 - 0.039 = 0.44
Half of the width is obtained by dividing the width by 2:
Half Width = 0.44 / 2 = 0.22
Therefore, the confidence interval 0.039 < p < 0.479 can be expressed as:
p ± E = 0.259 ± 0.22
So, the correct option is:
D. 0.259 ± 0.22
know more about confidence interval: brainly.com/question/32546207
#SPJ11
Gloria owns a video rental store. Two-fifths of the store items
are comedies, one-eighth are horror films, one-fourth are
dramas, and the remaining 270 are video games.
a. How many items are there in total?
b. How many comedies are there?
c. How many horror films are there?
Answers
Answer:
(a) 1200, (b) 480, (c) 150
Step-by-step explanation:
(a) Fraction of video games
= 1 - \(\frac{2}{5}\) - \(\frac{1}{8}\) - \(\frac{1}{4}\)
= \(\frac{40}{40}\) - \(\frac{16}{40}\) - \(\frac{5}{40}\) - \(\frac{10}{40}\)
= \(\frac{9}{40}\)
\(\frac9{40}\) = 270
\(\frac{1}{40}\) = 30
∴ \(\frac{40}{40}\) = 1200
∴ There are a total of 1200 items.
(b) ∴ No. of comedies = \(\frac{16}{40}\)
= 480
(c) ∴ No. of horror films = \(\frac{5}{40}\)
= 150
a normal population has a mean 31 and standard deviation 7. what is the probability that a randomly chosen value will be greater than 18?
Answers
Answer:
0.969
Step-by-step explanation:
use the z-score formula to convert the values.
z = (X - υ) / σ
where X is the test statistic, υ is the mean, σ is the standard deviation.
z = (18 - 31) / 7
= -1.857
area in z-score table (this is area to left of <18) is 0.0314.
P(>18) = 1 - 0.0314 = 0.969
4) [ 10pts] In a certain population, body weights are normally distributed. How many people must be surveyed if we want to estimate the percentage who weigh more than 190 pounds? Assume that we want 98% confidence that the error is no more than 3 percentage points.
Answers
To estimate the percentage of people who weigh more than 190 pounds with a 98% confidence and an error no more than 3 percentage points, a minimum sample size of 1064 people should be surveyed.
To estimate the desired percentage accurately, we need to determine the necessary sample size for our survey. Given that body weights are normally distributed in the population, we can use the concept of a confidence interval to calculate the sample size required.
First, we need to determine the standard deviation of body weights in the population. This information is crucial in calculating the sample size. However, since the standard deviation is not provided in the question, we cannot determine the exact sample size. We will make an assumption based on typical body weight distributions.
Next, we can use the formula for sample size calculation:
n = (Z^2 * p * q) / E^2
Where:
- n is the required sample size
- Z is the z-value corresponding to the desired confidence level (98% confidence corresponds to a z-value of approximately 2.33)
- p is the estimated proportion of people who weigh more than 190 pounds
- q is 1 - p
- E is the desired margin of error, which is 3 percentage points (0.03 in decimal form)
Assuming a normally distributed population, we typically assume p = q = 0.5 to obtain the maximum sample size required. However, since we want to estimate the percentage of people weighing more than 190 pounds, p is likely to be less than 0.5.
Without the information on the proportion p, we cannot determine the exact sample size. However, based on typical distributions and assuming p = 0.5, we can estimate the minimum sample size required to be 1064 people.
Learn more about sample size
brainly.com/question/30885988
#SPJ11
subtract
2×1/5−(−3×1/6)
Answers
Answer:
= 9/10
Step-by-step explanation:
- × - = +
Then:
2×1/5 = (2×1)/5 = 2/5 = 12/30
-(-3×1/6) = +(3*1)/6 = 3/6 = 15/30
Then:
2×1/5-(-3×1/6) = 2/5 + 3/6 = 12/30 + 15/30 = (12+15)/30 = 27/30
27/30 = 9/10
Details A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 35 ft/s. Its height in feet after t seconds is given by y = 35t - 14t². A. Find the average velocity for the time period beginning when t-1 and lasting .01 s: .005 s: .002 s: .001 s: NOTE: For the above answers, you may have to enter 6 or 7 significant digits if you are using a calculator. Estimate the instanteneous velocity when t=1. O Question 14 If f(x) = 3x² - 2x + 2, find f'(-4). 3x² - Use this to find the equation of the tangent line to the parabola y (-4, 58). The equation of this tangent line can be written in the form y = mx + b where m is: and where b is: 1 pt 1 Details 2x + 2 at the point
Answers
1. Average velocities (rounded to two decimal places):
a) 0.01 s: 19.94 ft/s
b) 0.005 s: [calculate using given values]
c) 0.002 s: [calculate using given values]
d) 0.001 s: [calculate using given values]
2. Instantaneous velocity at t = 1: 7 ft/s.
3. Equation of the tangent line to the parabola at (-4, 58): y = -26x - 46, where m = -26 and b = -46.
1. To find the average velocity for different time periods and estimate the instantaneous velocity, and also find the equation of the tangent line to the parabola at a specific point, we can follow the given details step by step.
Average velocity for the time period beginning when t = 1 and lasting:
a) 0.01 s:
Average velocity = (y2 - y1) / (t2 - t1)
y1 = 35(1) - 14(1)^2 = 21 ft
y2 = 35(1.01) - 14(1.01)^2 = 21.1994 ft
t1 = 1 s, t2 = 1.01 s
Average velocity = (21.1994 - 21) / (1.01 - 1) ≈ 19.94 ft/s (rounded to two decimal places)
b) 0.005 s:
Average velocity = (y2 - y1) / (t2 - t1)
Calculate using a similar approach as above.
c) 0.002 s:
Average velocity = (y2 - y1) / (t2 - t1)
Calculate using a similar approach as above.
d) 0.001 s:
Average velocity = (y2 - y1) / (t2 - t1)
Calculate using a similar approach as above.
Estimate the instantaneous velocity when t = 1:
To estimate the instantaneous velocity at t = 1, we can find the derivative of y with respect to t:
y = 35t - 14t²
dy/dt = 35 - 28t
At t = 1, the instantaneous velocity is dy/dt = 35 - 28(1) = 7 ft/s.
2. Find f'(-4) and use it to find the equation of the tangent line to the parabola at (-4, 58):
f(x) = 3x² - 2x + 2
To find f'(-4), we take the derivative of f(x):
f'(x) = 6x - 2
f'(-4) = 6(-4) - 2 = -26
3. The equation of the tangent line can be written in the form y = mx + b:
Using the point (-4, 58) and the slope m = f'(-4) = -26, we can substitute the values into the equation:
y - y₁ = m(x - x₁)
y - 58 = -26(x - (-4))
y - 58 = -26(x + 4)
y = -26x - 104 + 58
y = -26x - 46
Therefore, the equation of the tangent line to the parabola at (-4, 58) is y = -26x - 46, where m = -26 and b = -46.
Learn more about the equation of tangent line at
https://brainly.com/question/6617153
#SPJ4
what is the maximum value of f(x, y)=x^{2}-x-yf(x,y)=x 2 −x−y on the region where \{(x, y): 0 \leq x \leq 1,0 \leq y \leq 1\} ?{(x,y):0≤x≤1,0≤y≤1}?
Answers
The maximum value of f(x, y)=x2-x-y on the region where 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1 is 1.
To find the maximum value, we can set up a system of inequalities and solve it:
0 ≤ x ≤ 1
0 ≤ y ≤ 1
f(x, y)=x2-x-y
Since both x and y are greater than or equal to 0, their product will also be greater than or equal to 0. Therefore, the maximum value of the equation is when x = 1 and y = 0, since it maximizes the positive value of x2 while minimizing the negative value of -x-y. This means that the maximum value of f(x, y) is 1.
To know more about the region refer here:
https://brainly.com/question/30059816#
#SPJ11
The maximum value of f(x,y)=x^{2}-x-yf(x,y)=x 2 −x−y on the region where \{(x, y): 0 \leq x \leq 1,0 \leq y \leq 1\} is 0.
To find the maximum value, we need to find the critical points of the function and test them within the given region. The critical points are where the partial derivatives of the function are equal to 0.
The partial derivative with respect to x is:
f_x(x,y)=2x-1
The partial derivative with respect to y is:
f_y(x,y)=-1
Setting these partial derivatives equal to 0, we get:
2x-1=0 --> x=1/2
-1=0 --> no solution for y
So the only critical point within the given region is (1/2, y) for any value of y. However, since the partial derivative with respect to y is always -1, the function is decreasing with respect to y. Therefore, the maximum value will occur when y is at its smallest value, which is 0.
Plugging in x=1/2 and y=0 into the original function, we get:
f(1/2,0)=(1/2)^{2}-(1/2)-0=0
Know more about maximum value here:
https://brainly.com/question/30236354
#SPJ11
A particular type of diet cola advertises that each can contains 12 ounces of the beverage. each hour, a supervisor selects 10 cans at random, measures their contents, and computes a 95% confidence interval for the true mean volume. for one particular hour, the 95% confidence interval is 11.97 ounces to 12.05 ounces.
Answers
The estimated mean volume of the diet cola cans is between 11.97 and 12.05 ounces with 95% confidence for the particular hour.
This means that if the supervisor were to repeat this process many times, in 95% of the cases, the true mean volume of the diet cola cans would fall within the interval of 11.97 to 12.05 ounces.
The sample size of 10 cans selected at random is sufficient for this confidence interval to be accurate. This information can be used by the company to ensure that their cans are consistently filled to the advertised volume, and by consumers to have confidence in the volume of the product they are purchasing.
For more questions like Mean volume click the link below:
https://brainly.com/question/12059077
#SPJ11
Which one is correct for VIF of regression? Choose all applied.
a. Among Independent variables whose VIF is higher than 10, we eliminate one which is the least
related with dependent variable.
b. If there are 5 independent variables in a multiple regression, there are 5 VIF values available.
c. Among Independent variables whose VIF is higher than 10, we can eliminate more than one independent variables at the same time.
d. Elimination process of VIF is iterative process until all VIF values are smaller than 10 or close to 10.
Answers
The correct statements about the variance inflation factor (VIF) in regression are:
a. We eliminate one independent variable at a time from those with VIF higher than 10, starting with the one least related to the dependent variable.
c. It is possible to eliminate multiple independent variables simultaneously if their VIF values are higher than 10.
d. The elimination process of VIF is iterative until all VIF values are smaller than 10 or close to 10.
Statement b is incorrect because the number of VIF values available in a multiple regression is not necessarily equal to the number of independent variables.
Learn more about variance inflation factor here: brainly.com/question/29576995
#SPJ11