If using the method of completing the square to solve the quadratic equation x 2 + x + 9 = 0, which number would have to be added to "complete the square"?
Answers
Answer:
Below
Step-by-step explanation:
To complete the square, the coefficient of x^2 must be 1 ( it is already)
then take 1/2 of the x coefficient .... 1/2.... square it and add it to both sides of the equation
x^2 + x + 1/4 + 9 = 1/4
then you can reduce this to
( x+ 1/2)^2 + 9 = 1/4 for further 'solving'
Related Questions
To join the school swim team, swimmers must be able to swim at least 480 yards
without stopping. Let n represent the number of yards a swimmer can swim without
stopping. Write an inequality describing which values of n will result in a swimmer
making the swim team.
a)
nis greater than or equal to 480
b) n is less than or equal to 480
n is greater than 480
d)
n is less than 480
Answers
Answer:
A) n is greater than or equal to 480.
Step-by-step explanation:
The keyword "at least" means greater than or equal to.
How were the Phoenicians and the Israelites alike?
Both groups were Canaanites.
Both groups were Canaanites.
Both groups became powerful through trade.
Both groups became powerful through trade.
Both groups were monotheists.
Both groups were monotheists.
Both groups spread their ideas throughout the Mediterranean.
Answers
Which of the following differential equation(s) is/are linear? (Choose all that apply.) 1 2xy" - 5xy' + y = sin(3x) (v)² + xy =In(x) □y' + sin(y)=e3x (x²+1)y"-3y - 2x³y=-x-9 (+1)y'+xy=y"
Answers
To determine which differential equation(s) are linear, we need to examine the form of each equation. A linear differential equation is one that can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x), b(x), c(x), and g(x) are functions of x.
The differential equation 2xy" - 5xy' + y = sin(3x) is linear. It can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x) = 2x, b(x) = -5x, c(x) = 1, and g(x) = sin(3x).
The differential equation (v)² + xy = In(x) is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (v)², where v represents the derivative of y with respect to x. This term does not have a linear coefficient.
The differential equation y' + sin(y) = e^(3x) is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = sin(y), and g(x) = e^(3x).
The differential equation (x²+1)y" - 3y - 2x³y = -x - 9 is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (x²+1)y", where the coefficient is a function of x.
The differential equation y' + xy = y" is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = x, and g(x) = y".
Learn more about differential equation here
https://brainly.com/question/32524608
#SPJ11
cierra lends half of her pencils to her friend. cierra then buys four more pencils. now she has 12 pencils. how many pencils did cierra have to start with?
Answers
Cierra lends half of her pencils to her friend. Cierra then buys four more pencils, now she has 12 pencils. Therefore, Cierra initially had 16 pencils to start with.
Let's solve the problem step by step.
Let's assume the number of pencils Cierra started with is 'x'.
According to the problem, Cierra lends half of her pencils to her friend, which means she gives away x/2 pencils.
After giving away x/2 pencils, Cierra has (x - x/2) pencils left.
Next, Cierra buys four more pencils, so her total number of pencils becomes (x - x/2) + 4.
According to the problem, this total number is 12, so we can write the equation: (x - x/2) + 4 = 12
Now, let's solve this equation to find the value of x:
Multiplying through by 2 to eliminate the fraction:
2(x - x/2) + 2(4) = 2(12)
2x - x + 8 = 24
x + 8 = 24
x = 24 - 8
x = 16
Therefore, Cierra initially had 16 pencils.
To learn more about buys pencil visit:
brainly.com/question/17022702
#SPJ11
Brandon has 50 pears and 90 apples. Grug has 8329 times as many as 1/100th of the number of pears AND apples. how many pears of apples does Grug have?
Answers
Grugs apples and pears = 8329 * (0.1 * (140))
= 8329 * 1.4
= 11660.6
So either 11661 or just 11660 apples depending on if you’re supposed to round or not.
For each of the matrices in Exercises 1 through 13, find all real eigenvalues, with their algebraic multiplicities. Show your work. do not use technology. [5 -4 2 -1] [0 1 0 0 0 1 1 0 0] Consider the matrix A = [1 k 1 1], where k is an arbitrary constant. For which values of k does A have two distinct real eigenvalues? When is there no real eigenvalue? Consider the matrix A = [a b b -a], where a and b are arbitrary constants. Find all eigenvalues of A. Explain in terms of the geometric interpretation of the linear transformation T(x) = Ax.
Answers
The real eigenvalues and their algebraic multiplicities for the matrices in Exercises 1 through 13 are as follows: [Exercise 1: λ = 6 + √7 (multiplicity 1), λ = 6 - √7 (multiplicity 1)], [Exercise 2: No real eigenvalues], [Exercise 3: When k ≠ ±2, two distinct real eigenvalues; when k = ±2, no real eigenvalues].
Find all real eigenvalues, with their algebraic multiplicities, for each of the matrices in Exercises 1 through 13?To find the real eigenvalues and their algebraic multiplicities for the given matrix:
```
[5 -4 2 -1]
```
We need to find the eigenvalues by solving the characteristic equation:
```
|5 - λ -4 2 -1 |
| | = 0
|-4 5 - λ -1 2 |
```
Expanding the determinant, we get:
```
(5 - λ) * ((5 - λ) * 2 - (-4) * (-1)) - (-4) * (-1) * (-4 - (-1)) = 0
```
Simplifying further:
```
(5 - λ) * (10 - 2λ + 4) - 12 = 0
(5 - λ) * (14 - 2λ) - 12 = 0
14(5 - λ) - 2λ(5 - λ) - 12 = 0
70 - 14λ - 10λ + 2λ^2 - 12 = 0
2λ^2 - 24λ + 58 = 0
```
Now, we solve this quadratic equation for λ:
```
λ = (-(-24) ± sqrt((-24)^2 - 4 * 2 * 58)) / (2 * 2)
λ = (24 ± sqrt(576 - 464)) / 4
λ = (24 ± sqrt(112)) / 4
λ = (24 ± 4√7) / 4
λ = 6 ± √7
```
Therefore, the real eigenvalues are λ = 6 + √7 and λ = 6 - √7, each with an algebraic multiplicity of 1.
To find the real eigenvalues and their algebraic multiplicities for the given matrix:
[0 1 0]
[0 0 1]
[1 0 0]
We need to find the eigenvalues by solving the characteristic equation:
```
| -λ 1 0 |
| 0 -λ 1 | = 0
| 1 0 -λ |
```
Expanding the determinant, we get:
```
(-λ) * (-λ * (-λ) - 1 * 1) + 1 * (1 * (-λ) - 1 * (-λ * (-λ))) = 0
λ^3 + 1 = 0
```
This equation has no real solutions. Therefore, there are no real eigenvalues for this matrix.
For the matrix:
```
[1 k 1 1]
```
To find the values of k that result in two distinct real eigenvalues, we need to determine when the discriminant of the characteristic equation is positive.
The characteristic equation is:
```
|1 - λ k 1 1 |
| | = 0
|k 1 - λ 1 1 |
```
Expanding the determinant, we get:
```
(1 - λ) * ((1 - λ) - k * 1) - k * (1 - λ - 1) = 0
(1 - λ) * (1 - λ - k) - k * (-λ) = 0
(1 - λ)^2 - (1 - λ)k + kλ = 0
```
Expanding further:
```
1 -
Learn more about real eigenvalues
brainly.com/question/29888353
#SPJ11
PLSSS HELP IF YOU TURLY KNOW THISS

Answers
Answer:
1/4
Step-by-step explanation:
Can someone help me find the answer and explain please??

Answers
Answer:
75
Step-by-step explanation:
x = 5
Input 5 into the f(x) equation.
f(5) = 3(5)²
f(5) = 3 × 25
f(5) = 75
Hope that helps.
Answer:
75 is the correct answer for above questions.
The Van der Pol oscillator (describes oscillations in electrical circuits employing vacuum tubes) is described by the following second order differential equation: d^2 x/dt^2 −μ(1 −x^2) dx/dt + x = 0Let the initial conditions be: x(0) = 2, x'(0) = 0 (a) Rewrite the ODE as a system of first order ODES (b) Let = 1. Perform two iterations using Euler's method using a step size of 0.1 [10 (c) We are going to solve the above problem in Matlab using ode45. Write the mfile that defines the system of ODEs from part(a). This is the function call used by the ode solver)
Answers
(a) To rewrite the given second-order differential equation as a system of first-order differential equations, we introduce a new variable y = dx/dt. Then, the original equation becomes:
dx/dt = y
dy/dt = μ(1 - x^2)y - x
Thus, we have a system of two first-order differential equations in terms of the variables x and y.
(b) Using Euler's method with a step size of 0.1 and the initial conditions x(0) = 2 and x'(0) = 0, we can obtain the following table of values for the first two iterations:
t x(t) y(t)
0.0 2.0 0.0
0.1 2.0 -0.2
0.2 1.98 -0.395996
0.3 1.943203 -0.572175
0.4 1.894315 -0.728486
0.5 1.827662 -0.864283
0.6 1.748208 -0.979298
0.7 1.659462 -1.073651
0.8 1.56442 -1.147836
0.9 1.466409 -1.202743
1.0 1.36897 -1.239667
(c) The MATLAB function that defines the system of ODEs from part (a) is:
lua
Copy code
function dydt = vanderpol(t, y, mu)
dydt = [y(2); mu*(1-y(1)^2)*y(2)-y(1)];
end
Here, t is the independent variable, y is a vector of dependent variables (in this case, y = [x; y]), and mu is a parameter. The function returns a vector dydt containing the derivatives of x and y, respectively. This function can be used as the input to the ode45 solver to numerically solve the system of differential equations.
Learn more about equation here:
https://brainly.com/question/29657983
#SPJ11
What is the unit rate for miles per gallon?
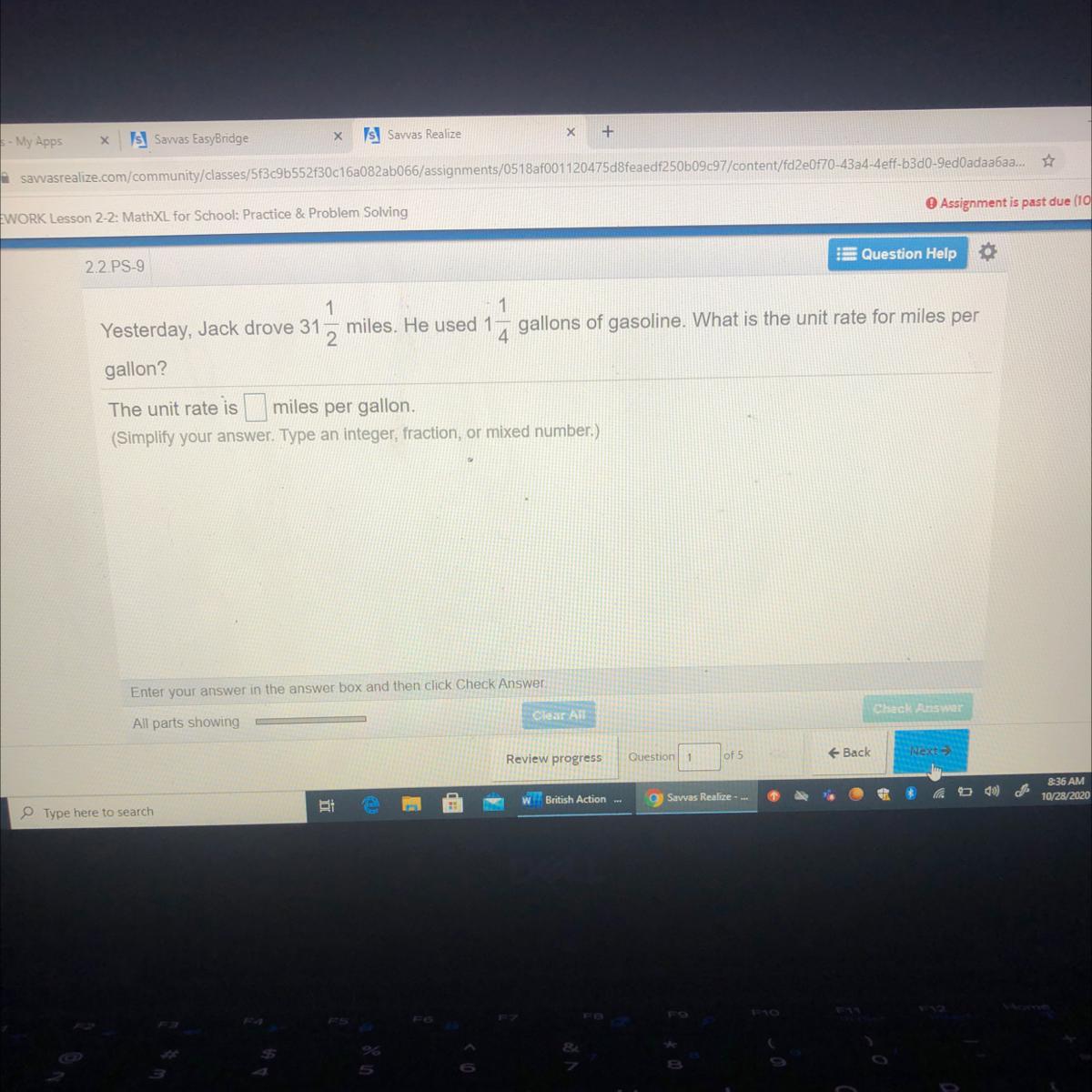
Answers
Answer:
24 to 6
Step-by-step explanation:
Answer:
the first answer is right
What is the value of x?

Answers
Answer:
x = 9
Step-by-step explanation:
→Looking at the angles, you can see that a right angle is formed. This means that there must be another right angle (90 degrees) formed with the numbers. You can set up the equation, like so:
3x + 6 + 57 = 90
→Add like terms (6 and 57):
3x + 63 = 90
→Subtract 63 from both sides:
3x = 27
→Divide both sides by 3:
x = 9
Answer:
x=9
Step-by-step explanation:
a right angle is 90 degrees
90-57= 33
33-6=27
27/3 = 9
Its my request to you to mark this as the brainiest
If A = 56, then find c

Answers
Answer:
Since A= 56 then B=56 so A+B=112
The whole tringle must be 180 degrees
So 180-112=68
SO C=68
I believe
the number of hits on the campus ready website follows a poisson process with a rate of 3 per minute. what is the probability that more than a minute foes by without a hit
Answers
The probability that more than a minute foes by without a hit is 0.0498.
Let X denote the waiting time in minutes until the next hit.
From the question, we have
The probability density function of exponential distribution is,
f(x)=λe^(-λ*) λ>0
Probability =
P(X>1) =∫_1^∞ 3e^(-3x) dx
=3(e^(-3z)/(-3))_1^∞
=e^(-3)
=0.0498
Probability = 0.0498
Probability:
Possibility is referred to as probability. This branch of mathematics deals with the occurrence of a random event. The value's range is 0 to 1. Probability has been applied into mathematics to predict the likelihood of different events. Probability generally refers to the degree to which something is likely to occur. This fundamental theory of probability, which also applies to the probability distribution, can help you comprehend the possible outcomes for a random experiment. Gonna determine how likely something is to occur, use probability. Many things are hard to predict with 100% certainty. We can only anticipate the possibility of an event occurring using it, or how likely it is.
To learn more about probability visit: https://brainly.com/question/11234923
#SPJ4
A box is to be made out of a 10 cm by 20 cm piece of cardboard. Squares of side length cm will be cut out of each corner, and then the ends and sides will be folded up to form a box with an open top. (a) Express the volume V of the box as a function of x. V = cm^3 (b) Give the domain of V in interval notation. (Use the fact that length and volume must be positive.) = ? (c) Find the length L , width W, and height H of the resulting box that maximizes the volume. (Assume that W < or = to L ) L= ?cm W= ?cm H= ? cm (d) The maximum volume of the box is ? cm^3.
Answers
(a) The volume V of the box as a function of x is V = 4x^3-60x^2+200x
(b) The domain of V in interval notation is 0<x<5,
(c) The length L , width W, and height H of the resulting box that maximizes the volume is H = 2.113, W = 5.773, L= 15.773
(d) The maximum volume of the box is 192.421 cm^2.
In the given question,
A box is to be made out of a 10 cm by 20 cm piece of cardboard. Squares of side length cm will be cut out of each corner, and then the ends and sides will be folded up to form a box with an open top.
(a) We have to express the volume V of the box as a function of x.
If we cut out the squares, we'll have a length and width of 10-2x, 20-2x respectively and height of x.
So V = x(10-2x) (20-2x)
V = x(10(20-2x)-2x(20-2x))
V = x(200-20x-40x+4x^2)
V = x ( 200 - 60 x + 4x^2)
V = 4x^3-60x^2+200x
(b) Now we have to give the domain of V in interval notation.
Since the lengths must all be positive,
10-2x > 0 ≥ x < 5 and x> 0
So 0 < x < 5
(c) Now we have to find the length L , width W, and height H of the resulting box that maximizes the volume.
We take the derivative of V:
V'(x) = 12x^2-120x+200
Taking V'(x)=0
0 = 4 (3x^2-30x+50)
3x^2-30x+50=0
Now using the quadratic formula:
x=\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
From the equationl a=3, b=-30, c=50
Putting the value
x=\(\frac{30\pm\sqrt{(-30)^2-4\times3\times50}}{2\times3}\)
x= \(\frac{30\pm\sqrt{900-600}}{6}\)
x= \(\frac{30\pm\sqrt{300}}{6}\)
x= \(\frac{30\pm17.321}{6}\)
Since x<5,
So x= \(\frac{30-17.321}{6}\)
x= 2.113
So H = 2.113, W = 5.773, L= 15.773.
d) Now we have to find the maximum volume of the box.
V = HWL
V= 2.113*5.773*15.773
V = 192.421 cm^3
To learn more about volume of rectangle link is here
brainly.com/question/13798973
#SPJ4
Solve for x. Leave your answer in the simplest form.
Image down below!
Please help! Brainlist and points

Answers
Apply Pythagorean theorem
H²=9²+5²H²=81+25H²=106So
x²=106+4²x²=106+16x²=122x=√122x=11.04≈11Answer:
√(122)
Step-by-step explanation:
Pythagoras Theorem: a² + b² = c²
(where a and be are the legs, and c is the hypotenuse, of a right triangle)
First, find the length of the hypotenuse of the triangle with legs of 9 and 5 units:
⇒ 5² + 9² = c²
⇒ 25 + 81 = c²
⇒ c² = 106
⇒ c = √(106)
Therefore √(106) is the longest leg of the other triangle.
So we can now use this measurement to find x (the hypotenuse) of the other triangle:
⇒ 4² + √(106)² = c²
⇒ 16+ 106 = c²
⇒ c² = 122
⇒ c = √(122)
You have $48 to buy tickets at the carnival. The tickets cost $8 for 15 tickets. How many tickets can you buy? 9 The water ride costs 12 tickets, and the ferris wheel costs 15 tickets. You want to ride the water ride 3 times and ride the ferris wheel 3 times. How many tickets do you have remaining? 9 A. 12 B. 9 C. 7
Answers
Answer:
the answer would be 9 tickets left
Step-by-step explanation:
8x6=48
15x6=90
12x3 + 15x3=81
90-81=9
9 tickets left
Julio says,"If you subtract 15 from my number and multiply the difference by -7,the result is -175." What is Julios number
Answers
Answer: 40
Step-by-step explanation:
Assume Julio's number is x.
The expression would be:
-7 * (x - 15) = -175
x - 15 = -175/-7
x = -175/-7 + 15
x = 40
WHEN DOING PROOFS IF B IS THE MIDPOINT OF LINE AC AND MEASURE A IS CONGRUENT TO MEASURE C AND ANGLE 1 IS CONGRUENT TO ANGLE 2. WOULD B BE A SIDE?
Answers
On solving the provided question, we can say that - B= 20 and by the help of SAS Congruency Δ ABD ≅ Δ ACD
What is isosceles triangle?A triangle having two equal sides is known as an isosceles triangle in geometry. The equilateral triangle is a specific instance of a triangle that can have exactly two sides that are the same length or at least two sides that are. Two equal sides and two equal angles make up an isosceles triangle. Greek words iso (equal) and skelos are the source of the name (leg). A scalene triangle is a triangle without any sides, whereas an equilateral triangle is one with all equal sides.
given ABC is isosceles triangle
\(= > /B =/C\)
D is midpoint of BC
\(= > BD = DC\\3x+10 = 70\\3x=70-10\\x=60/3\\x=20\\B = 20\\\)
IN Δ ABD and Δ ACD
\(AB = AC (given)\\B = C\\BD = DC\)
So, as SAS congruency rule
Δ ABD ≅ Δ ACD
To know more about isosceles triangle visit:
https://brainly.com/question/2456591
#SPJ4
What is the Lowest common multiple of eight and six
Answers
Answer:
24
Step-by-step explanation:
8= 8, 16 ,24 , 32 , 40, 48, 56, 64, 72, 80
6= 6, 12, 18, 24, 30, 36, 42, 48, 54, 50
Answer:
Step-by-step explanation:
Yo come let's talk
then
0 A community center offers classes for students.
. The range of the number of students in each class is 13.
. The median number of students in each class is 9.
Which of the following box-and-whisker plots could represent the numbers of students in the classes?
Numbers of Students
Numbers of Students
in Classes
in Classes
C₂
+++
2 4 6 8 10 12 14 16 18 20 22 24
Numbers of Students
in Classes
+++
2 4 6 8 10 12 14 16 18 20 22 24
B.
D.
++
2 4 6 8 10 12 14 16 18 20 22 24
Numbers of Students
in Classes
+111*
2 4 6 8 10 12 14 16 18 20 22 24
T
Answers
The response is A.
Option A's median value is 9, and its range is 13, therefore the smallest value is 9-6, which equals 3, and the greatest value is 9+6, which equals 15. This information is accurately represented by the box-and-whisker plot in option A.
what is the range?The difference between the highest and lowest values for a given data collection is the range in statistics. For instance, the range will be 10 - 2 = 8 if the given data set is 2, 5, 8, 10, and 3.
As a result, the range may alternatively be thought of as the distance between the highest and lowest observation. The range of observation is the name given to the outcome. Statistics' range reflects the variety of observations.
from the question:
According to the information provided, the number of pupils in each class might range from 9+6 = 15 to 9+6 = 3. Because the maximum value exceeds 15, options C and D cannot accurately represent the number of students in the classes.
Option A's median value is 9, and its range is 13, therefore the smallest value is 9-6, which equals 3, and the greatest value is 9+6, which equals 15. This information is accurately represented by the box-and-whisker plot in option A.
Option B's median value is 9, but its range (from 9-5 = 4 to 9+5 = 14) is only 11, which is less than the range that could be achieved by the number of students. As a result, option B cannot accurately reflect the number of students enrolled in each class.
Thus, the response is A.
to know more about range visit;
https://brainly.com/question/28135761
#SPJ9
you roll two fair dice. find the probability that the first die is a 6 given that the minimum of the two numbers is a 4.
Answers
The probability of getting the 6 on the first die given that the minimum of two numbers is 4 would be 0.11.
What is the probability?
Probability is a branch of mathematics that deals with numerical descriptions of how likely an event is to occur or how likely a proposition is to be true. The probability of an event is a number between 0 and 1, where 0 indicates the event's impossibility and 1 indicates certainty.
Two dice are rolled.
Then the sample space (n) = 36
Possible outcomes = {(6,1), (6, 2), (6, 3), (6, 4)}
Probability = 4/36
= 0.11
Hence, the probability of getting the 6 on the first die given that the minimum of two numbers is 4 would be 0.11.
To learn more about probability in mathematics, visit:
brainly.com/question/24756209
#SPJ4
A spinner has a 45% chance of landing on green. What is the probability of the spinner first not landing on green, spun again, and then landing on green?
Answers
The probability of the spinner first not landing on green, spun again, and then landing on green is P ( A ) = 0.2475
Given data ,
Let the probability of the spinner first not landing on green, spun again, and then landing on green is P ( A )
Now , the probability that spinner landing on green = 0.45
And , the probability that spinner not landing on green = 0.55
So , P ( A ) = probability that spinner landing on green x probability that spinner not landing on green
P ( A ) = 0.45 x 0.55
P ( A ) = 0.2475
Hence , the probability is 0.2475
To learn more about probability click :
https://brainly.com/question/17089724
SPJ1
mickel and 4 friend bought a total of 95 raffle tickets if the ticket were dived equaly among themselves how many tickets did each person get?
Answers
Answer:
19
Step-by-step explanation:
5 people in total, divide equally from 95
Answer:
Step-by-step explanation:
95/4=23.75
Round 23.75 --> 24.00 raffle tickets each.
For the line that has the equation 3 x_1 +5 x_2=30, an axis intercept is: A) (10,6) B) (0,8) C) (6,10) D) (10,0)
Answers
The equation 3x₁ + 5x₂ = 30 intersects the x₁-axis at point D (10, 0) and the x₂-axis at point C (0, 6). Option B (0, 8) is not an intercept on the x₂-axis. Option C (6, 10) is not an intercept on the x₁-axis. The correct answer is option D (10, 0) as the x₁-axis intercept.
The equation given is 3x₁ + 5x₂ = 30. To find the axis intercept, we need to determine the points at which the line intersects the x₁ and x₂ axes. To find the x₁-axis intercept, we set x₂ = 0 and solve for x₁ 3x₁ + 5(0) = 30 3x₁ = 30
x₁ = 10
So, the x₁-axis intercept is (10, 0) which corresponds to point D in the given options. To find the x₂-axis intercept, we set x₁ = 0 and solve for x₂: 3(0) + 5x₂ = 30 5x₂ = 30 x₂ = 6 Therefore, the x₂-axis intercept is (0, 6) which corresponds to point C in the given options. To summarize, the equation 3x₁ + 5x₂ = 30 intersects the x₁-axis at point D (10, 0) and the x₂-axis at point C (0, 6).
In the given options, option A (10, 6) is not an intercept on either axis. Option B (0, 8) is not an intercept on the x₂-axis. Option C (6, 10) is not an intercept on the x₁-axis. The correct answer is option D (10, 0) as the x₁-axis intercept.
Remember, the x₁-axis intercept is found by setting x₂ = 0, and the x₂-axis intercept is found by setting x₁ = 0 in the equation.The correct answer is option D
Know more about intercept here:
https://brainly.com/question/14180189
#SPJ11
Given 4 and one tenth times negative 4 times 5 over 12, determine the product. negative 16 and 5 over 120 16 and 5 over 60 negative 6 and five sixths 6 and five sixths
Answers
The value of the expression \(4\frac{1}{10}\times-4\times\frac{5}{12}\) is \(-6\frac{5}{6}\).
What is a numerical expression?A mathematical statement expressed as a string of numbers and unknowable variables is known as a numerical expression. Statements can be used to create numerical expressions.
The given, expression is \(4\frac{1}{10}\times-4\times\frac{5}{12}\).
= (41/10) × (- 4) × (5/12).
= (41×-4×5)/(10×12).
= (-820/120).
= - 82/12.
= - 41/6.
= \(-6\frac{5}{6}\).
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
arranging indistinguishable such that no two are in the same row or column. how many ways can he do this?
Answers
When arranging indistinguishable objects in such a way that no two objects are in the same row or column, the number of possible arrangements depends on the dimensions of the grid.
The number of ways to arrange indistinguishable objects without any repetitions in a grid, such that no two objects are in the same row or column, depends on the dimensions of the grid. Let's assume the grid has M rows and N columns. In this case, the number of possible arrangements can be determined using combinatorics.
To find the total number of arrangements, we start with the first column. There are M choices for the first object in this column. Moving to the second column, there are M-1 choices since we need to avoid repetition within the same row. Continuing this process, the number of choices decreases by 1 for each subsequent column.
Therefore, the total number of arrangements can be calculated as M x (M-1) x (M-2) x ... x (M-N+1), where N is the number of columns. This can be further simplified as M! / (M-N)!, where "!" represents the factorial operation.
In conclusion, when arranging indistinguishable objects in a grid such that no two objects are in the same row or column, the number of possible arrangements depends on the dimensions of the grid. By applying combinatorial principles, the total number of arrangements can be calculated using the formula M! / (M-N)!.
To know more about factorial operation click here:
brainly.com/question/29105321
#SPJ11
Can someone help me solve for i
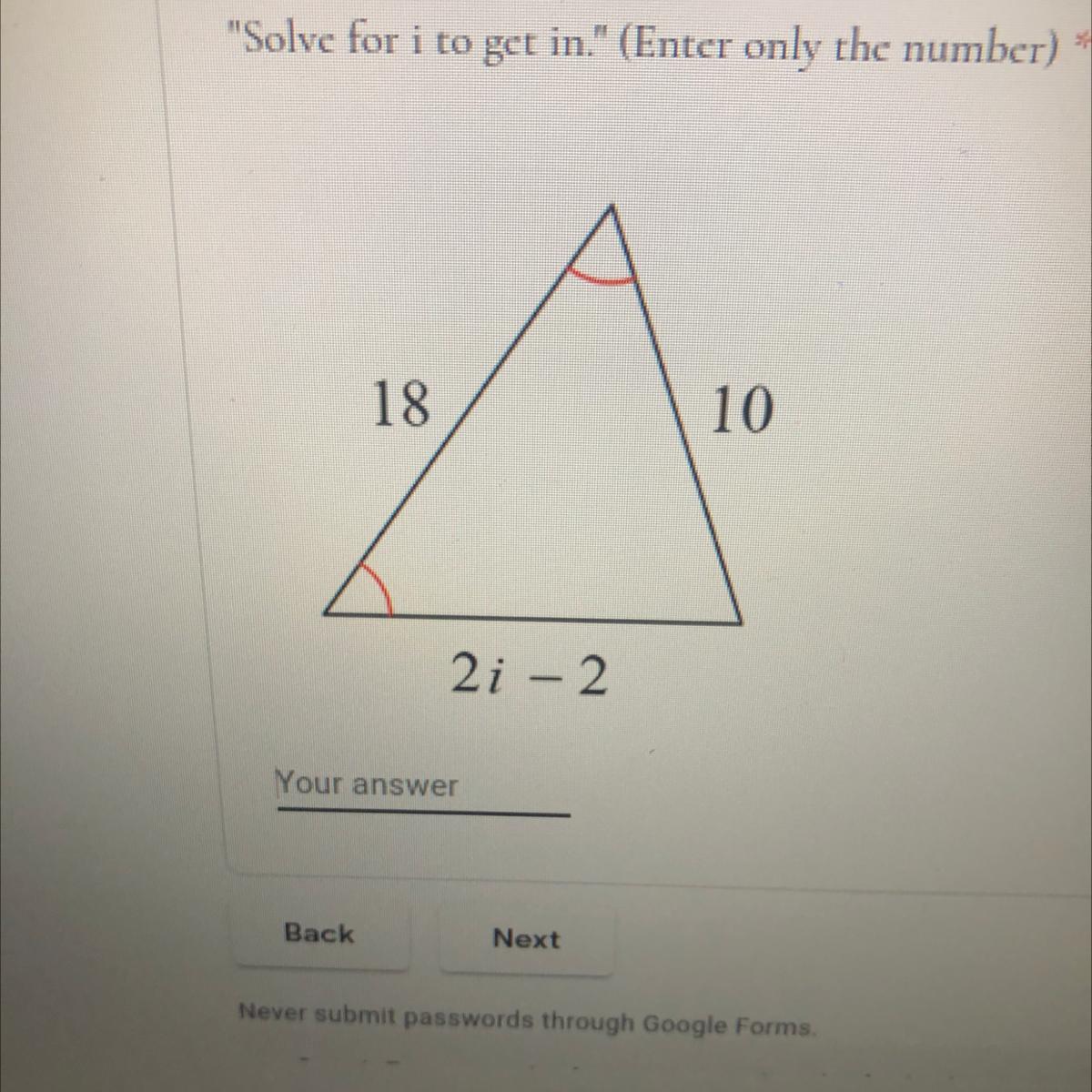
Answers
9514 1404 393
Answer:
i = 6
Step-by-step explanation:
The triangle is marked as isosceles, so the sides opposite the congruent angles have the same length.
10 = 2i -2
5 = i -1 . . . . . divide by 2
6 = i . . . . . . .add 1
which relation is a function

Answers
a function is a relationship between inputs where each input is related to exactly one output.
The relation in option B is a function.
What is Function?A function is a relation from a set A to a set B where the elements in set A only maps to one and only one image in set B. No elements in set A has more than one image in set B.
Given are 4 relations, A, B, C, D.
From the definition of function, it is clear that, no input value have more than one output value.
A : The value of x = -2 is mapping to 2, 1, 0, -1.
That is, an input value is having more than one output values.
So this is not a function.
B : Here the input values, 0, 1, 2 and 3 maps to -2.
Here the input values are distinct. No input values are mapping to more than one output value.
So this is a function.
C : Here 1 is mapping to -2 and 3. So not a function.
D : For x = 0, there are two y values, 3 and -3.
So this is not a function.
Hence option B is a function.
Learn more about Relations and Functions here :
https://brainly.com/question/6241820
#SPJ2
17.2 x 4.6 show working out in column method
Answers
Answer:
17.02
Step-by-step explanation:
2
41
17.2
x4.6
1
1022
+6880
17.02
be sure to cross out the 41 on the second line when you start multiplying 17.2 by 4
What is 0.9 quantile?
Answers
The 0.9 quantile, also known as the 90th percentile, is a measure used in statistics to indicate the value below which a certain percentage of observations in a data set falls.
Specifically, the 0.9 quantile represents the value below which 90% of the data falls, and above which only 10% of the data falls.
For example, if we have a data set of test scores for a class of 50 students, the 0.9 quantile score would be the score below which 90% of the students scored, and above which only 10% of the students scored.
This measure is useful in analyzing data sets and can provide information about the distribution of the data, such as whether it is skewed or symmetric, and can also be used to compare different data sets.
To know more about quantile here
https://brainly.com/question/30588709
#SPJ4