if x - 1/x = 5 , find the value of x^2 + 1/m^2 and (x + 1/x^2)
Answers
Answer:
Link to the Answer:
https://brainly.in/question/28630467
Step-by-step explanation:
Hope it Helps!!!!

Related Questions
you have a 10 mile one way distance to commute to work. the cost of your travel time is $60/hour. weather is not a factor. which mode should you use to commute?
Answers
Driving a personal car would be the most cost-effective mode of transportation for this commute, with a total daily cost of approximately $4.60 ($3.60 for gas + $1 for travel time).
Based on the given information, the most cost-effective mode of transportation for this commute would be to drive a personal car. Taking public transportation or carpooling may be more environmentally friendly options, but they may not save as much money as driving alone.
Assuming an average speed of 60 miles per hour on the highway, the commute would take approximately 20 minutes each way, or 40 minutes round-trip. This means the total cost of travel time for each workday would be $40 ($60/hour x 2/3 hour).
Using a cost calculator such as GasBuddy, we can estimate that the cost of driving 20 miles per day (round-trip) would be around $3.60 per day, assuming an average fuel efficiency of 25 miles per gallon and a gasoline price of $2.50 per gallon.
To know more about average speed visit:
https://brainly.com/question/10449029
#SPJ11
Which relation in the below table(s) represents a function?
Answers
The relation 2 represents a function.
In order to determine which relation in the below table represents a function, we need to first understand what a function is.A function is a relationship in which each input value corresponds to exactly one output value.
To put it another way, each x-value has one and only one y-value. The most typical method to determine whether a relation is a function is to use the vertical line test.
The vertical line test is a way to determine if a relation is a function graphically. To test if a graph is a function, we draw a vertical line through each x-value on the graph. If a vertical line crosses the graph more than once, it is not a function.
If, on the other hand, the graph passes the vertical line test and no vertical line crosses the graph more than once, it is a function.Now let's look at the table below to determine which relation is a function.
We will first plot the x and y values of each relation on a coordinate system and then apply the vertical line test to each relation.
Relation 1: x | y0 | 10 | 11 | 22 | 23 | 34 | 35 | 4Relation 1 does not represent a function since we can draw a vertical line through x = 3 and the line will cross the graph more than once.
Relation 2: x | y2 | 33 | 34 | 45 | 46 | 57 | 5Relation 2 represents a function since we can draw a vertical line through each x-value on the graph and it will only cross the graph once.
To learn more about : relation
https://brainly.com/question/30056459
#SPJ8
In Exercises 1 and 2, use a ruler to measure the length of the segment to the
nearest eighth of an inch.
Answers
Answer:
Time to sleep bro
Step-by-step explanation:
have sweet dreams
In the college class, there were 15 students that came to the review class before the test. This was 30% of the students in class. How many students were in the class, altogether?
Answers
Answer:
30 students
Step-by-step explanation:
The 15 students that came were 30% of the class:
30% = 15 students
To find 100%, we can first find 10% by dividing both sides by 3
10% = 3 students
(30% ÷ 3 = 10%, 15 ÷ 3 = 5)
Then, multiply both sides by 10 to get 100%
100% = 30 students
(10% × 10 = 100, 3 × 10 = 30)
1 of 6
© As an estimation we are told 5 miles is 8 km.
Convert 25.9 miles to km.
Answers
Answer:
41.68201 km=25.9 miles
Step-by-step explanation:
Answer:
Step-by-step explanation:
5m=8k
25.9m = ?k
25.9/5 = 5.18
5.18 X 9 = 46.62
Therefore 25.9 miles is 46.62 km
If J=91 ,L=16 , and K=73 , list the sides of triangle JKL in order from smallest to largest
A. JL, KJ, LK
B. LK, JL, KJ
C. KJ, JL, LK
D. KJ, LK, JL

Answers
JL, LK, JK are the smallest angle of a triangle is located across from its smallest side. The biggest side is on the other side of the biggest side.
How are the angles arranged, from greatest to smallest?JKL, where K is the specified angle, is an example.Acute Angles are the smallest angles. An acute angle is a particular kind of angle that measures less than 90°.an acute angle. The planar surface typically produces obtuse angles.Straight angle. Right angle.Subtract the squares of the other sides, then calculate the square root to determine the shorter side.Reflex angle at its widest point.JL, LK, JK are the smallest angle of a triangle is located across from its smallest side. The biggest side is on the other side of the biggest side.To learn more about smallest angle refer to:
https://brainly.com/question/12260821
#SPJ1
Help me do my ixl’s please

Answers
Answer:
24
Step-by-step explanation:
56/7 = 8
56 is 8 times 7, so you need 8 times 3.
8 × 3 = 24
7:3 = 56:24
Answer:
24
Step-by-step explanation:
7 is being multiplied by 8 so just multiply 3 by 8 witch will give you 24
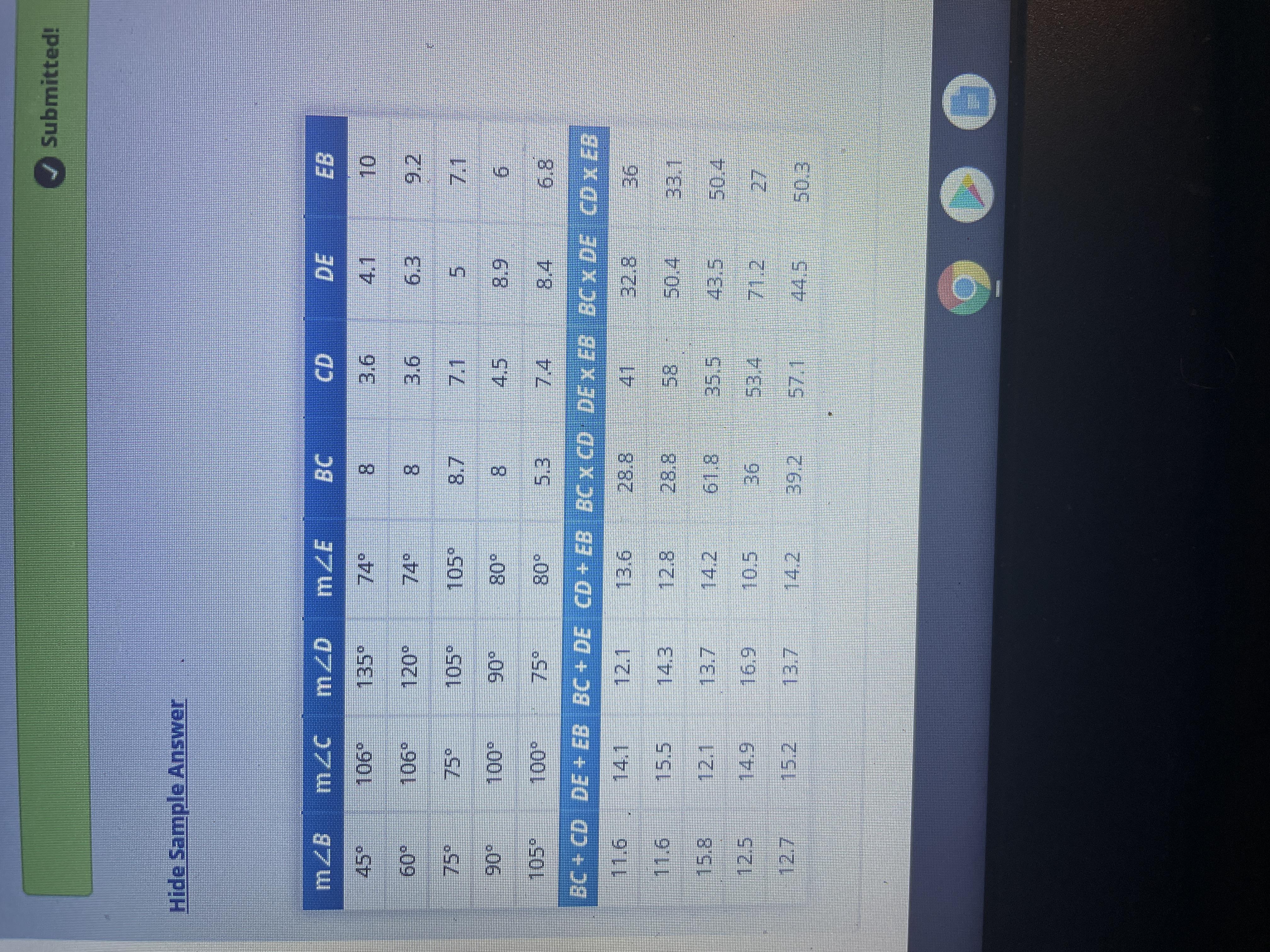
Once again, move points C, D, and E on the circle, and complete the table below. This time, you’ll consider what happens to the lengths of the sides of quadrilateral BCDE. Notice that m∠B is predetermined, so set that angle measure first.


Answers
Answer:
Also to help some of you out here’s the answer to question 6 !!
Question 6 : No apparent relationship exist between the side lengths of quadrilateral BCDE inscribed in circle A
Step-by-step explanation:
Rewrite in vertex form by completing the square:
x^2+4x+3x
Answers
The required equation of a parabola expressed in vertex form is f(x) = (x + 2)² - 1.
What is the parabola in vertex form?The equation of a parabola expressed in vertex form is
y = a(x - h)² + k
Where a is a multiplier and (h, k) are the coordinates of the vertex
The expression is given in the question as
f(x) = x² + 4x + 3
To complete the perfect square:
We have to add/subtract ( half the coefficient of the x- term )² to x² - 4x
f(x) = x² + 2(2)x + 4 - 4 + 3
f(x) = (x + 2)² - 1
Thus, the required equation of a parabola expressed in vertex form is f(x) = (x + 2)² - 1.
Learn more about the parabola here:
brainly.com/question/4074088
#SPJ1
The n-Firm Cournot Model) Suppose there are n≥2 firms in the Cournot oligopoly model. Let qi denote the quantity produced by firm i, and let Q=q1+⋯+qn denote the aggregate production level. Let P(Q) denote the market price (when demand equals Q ) and assume that demand function is given by P(Q)=a−Q (where Q
If we model firms' production decisions as a static game with complete information, can you show the normal-form representation of this game?
Answers
In the n-Firm Cournot Model, where there are n≥2 firms, each firm determines the quantity it produces in a Cournot oligopoly. The aggregate production level, denoted as Q, is the sum of the quantities produced by all the firms (q1+⋯+qn).
To represent this game as a static game with complete information, we can use the normal-form representation. In the normal-form representation, we describe the strategies and payoffs of each firm.
Let's go through the steps to create the normal-form representation of this game:
1. Identify the players: In this case, the players are the n firms participating in the Cournot oligopoly.
2. Determine the strategies: Each firm chooses the quantity it will produce, denoted by qi, where i represents the firm number. The quantity produced by each firm is the strategy of that firm.
3. Define the payoff function: The payoff for each firm depends on the market price, which is determined by the aggregate production level Q. The market price, P(Q), is given by the demand function P(Q) = a - Q.
4. Calculate the payoff for each firm: The payoff for each firm depends on the quantity it produces and the market price determined by the aggregate production level. The payoff can be calculated using the formula πi = P(Q) * qi, where πi represents the payoff for firm i.
5. Construct the normal-form representation: The normal-form representation is typically presented as a matrix, where each row represents a strategy profile (combination of quantities produced by the firms) and each column represents a player's strategy (quantity produced by a single firm). The entries in the matrix represent the payoffs for each firm.
For example, let's consider a 3-firm Cournot oligopoly with demand function P(Q) = a - Q. Firm 1, 2, and 3 have the strategies q1, q2, and q3, respectively. The payoffs can be calculated as follows:
- Payoff for firm 1: π1 = (a - Q) * q1
- Payoff for firm 2: π2 = (a - Q) * q2
- Payoff for firm 3: π3 = (a - Q) * q3
The normal-form representation matrix would look like this:
| Firm 1\2\3 | q1 | q2 | q3 |
|------------|--------|--------|--------|
| q1 | π1,1 | π1,2 | π1,3 |
| q2 | π2,1 | π2,2 | π2,3 |
| q3 | π3,1 | π3,2 | π3,3 |
Each entry in the matrix represents the payoff for each firm based on the combination of quantities produced by the firms.
To know more about payoff function refer to:
https://brainly.com/question/32760850
#SPJ11
Which set of numbers CANNOT represent the lengths of the sides of a triangle?
O A. 9, 12, 19
O B. 7, 5, 6
C. 6, 8, 11
O D. 7, 18, 11
Answers
Answer:
D
Step-by-step explanation:
The problem with D is that 7 + 11 = 18. The rule is any two sides must exceed the third. D gives the shorter + the middle length = the longest length.
That can't work. All the others are fine.
determine whether the series is convergent or divergent. [infinity] 6 en 3 n(n 1) n = 1 convergent divergent if it is convergent, find its sum. (if the quantity diverges, enter diverges.)
Answers
The given series is convergent and its sum is 6e.
Given series is [∞] 6en 3 / n(n+1);
n = 1.
The given series can be written as:
[∞] 6en 3 / n(n+1)
= [∞] 6en (1/n - 1/(n+1));
n = 1
It is a telescoping series.
Therefore, the nth term is given by the expression:
an = 6en (1/n - 1/(n+1))an
= 6en / n(n+1)
We need to check whether the series is convergent or divergent.
Using the Integral Test we can determine whether the series is convergent or divergent.
Let's use this test for our given series:
Integral test, ∫[1,∞] 6en / n(n+1) dn
6∫[1,∞] en / n(n+1) dn
By comparing this expression with the known integral function:
∫[1,∞] 1 / xα dx;
α > 1
Here, α = 2.
So, we can write:
nα = n²
Therefore, ∫[1,∞] 1 / n² dn
Consequently, we can solve the above integral as follows:
6∫[1,∞] en / n(n+1) dn
= 6[en/(n+1)] [1,∞)
= 6en / (n+1) |[1,∞)
Substituting the values, we get:
6en / (n+1)|[1,∞)
= 6e
Here, the value is a finite quantity.
Therefore, the given series is convergent and its sum is 6e.
To know more about series visit:
https://brainly.com/question/30457228
#SPJ11
Challenge #5: Shade all the points but leave the targets exposed with the fewest inequalities
Answers
The inequalities equation which will shade all the points except target point are, y >= 2, y >= -3.5x + 4.5 and y <= 1.25x - 1.5.
The line passing through P(-1,2) and P(-4,2) has a slope of 0 and a y-intercept of 2, so its equation is y = 2. The line passing through P(-1,2) and P(-2,0.5) has a slope of -3.5 and a y-intercept of 4.5, so its equation is y = -3.5x + 4.5. The line passing through P(-2,0.5) and P(-4,2) has a slope of 1.25 and a y-intercept of -1.5, so its equation is y = 1.25x - 1.5.
Now we can create a system of inequalities that will shade all of the points except for T(-2,2). We can do this by making sure that the inequality for each line is greater than or equal to the target point on one side of the line, and less than or equal to the target point on the other side of the line.
For the line y = 2, we can write the inequality y >= 2 on the side of the line that contains the target point T(-2,2). For the line y = -3.5x + 4.5, we can write the inequality y >= -3.5x + 4.5 on the side of the line that contains the point T(-2,2). For the line y = 1.25x - 1.5, we can write the inequality y <= 1.25x - 1.5 on the side of the line that contains the point T(-2,2).
Putting all of these inequalities together, we get:
y >= 2 (for the line passing through P(-1,2) and P(-4,2))
y >= -3.5x + 4.5 (for the line passing through P(-1,2) and P(-2,0.5))
y <= 1.25x - 1.5 (for the line passing through P(-2,0.5) and P(-4,2))
These inequalities should shade all of the points except for the target point T(-2,2), and they should do so with the fewest number of inequalities possible.
To know more about inequalities, here
brainly.com/question/30219862
#SPJ4
--The complete question is, With the fewest inequalities, shade all the points but leave the targets exposed. Write the inequality equations to do this.
Points are P(-1,2), P(-4,2) and P(-2, 0.5)
T(-2,2)
Graph is show in the image.--

I need this solved ASAP please
ratio 4:12 simplified.
Answers
Answer:
1/3
Step-by-step explanation:
4/12
2 goes in to 4 and 12, so 4 divide by 2 is 2 and 12 divide by 2 is 6 then you have to simplify it again since 2 can still go into 2 and 6 so 2 divide by 2 is 1 and 6 divide by 2 is 3.
Please show all work and not just the answers. Please help ASAP!!!!!

Answers
9514 1404 393
Answer:
a) x = 14
b) NP = 2 2/9; NL = 2 7/9
Step-by-step explanation:
a) The similarity statement tells you that angle P and angle L have the same measure:
angle L = angle P
3x +18 = 60
x + 6 = 20 . . . . . divide by 3
x = 14 . . . . . . . . . subtract 6
__
b) The proportional segments are ...
PN/NQ = LN/NM
y/3.2 = (5 -y)/4
5y = 4(5 -y) . . . . . multiply by 16
9y = 20 . . . . . . . . add 4y
y = 20/9 = NP
5 -y = (45 -20)/9 = 25/9 = NL
Are my answers correct? Will give points if not correct can you solve please

Answers
The area of the smaller sector or minor sector is 125.66 yd².
The area of the larger sector or major sector is 326.73 yd².
What are the areas of the sector?The areas of the minor and major sectors is calculated by applying the following formulas follow;
Area of sector is given as;
A = (θ/360) x πr²
where;
r is the radius of the sectorθ is the angle of the sectorThe area of the smaller sector or minor sector is calculated as follows;
A = ( 100 / 360 ) x π ( 12 yd)²
A = 125.66 yd²
The area of the larger sector or major sector is calculated as follows;
θ = 360 - 100
θ = 260⁰
A = ( 260 / 360 ) x π ( 12 yd)²
A = 326.73 yd²
Learn more about area of sector here: https://brainly.com/question/30607726
#SPJ1
The pre-image is...
What does a pre image mean
Answers
Answer:
i think it means pre image (plural pre images) (mathematics) For a given function, the set of all elements of the domain that are mapped into a given subset of the codomain; (formally) given a function ƒ : X → Y and a subset B ⊆ Y, the set ƒ−1(B) = {x ∈ X : ƒ(x) ∈ B}. The pre image of under the function is the set .
Step-by-step explanation:
Answer:
I forgot what the letter was for this option but The Pre image is a geometric shape BEFORE a transformation occurs ( I think that's option B but u should read it to be sure)
Step-by-step explanation:
Hope this helps I was kinda paying attention
a spherical golf ball is measured to have a radius of $$5 mm, with a possible measurement error of $$0.1 mm. what is the possible change in volume? use differential to estimate the error when computing the volume.
Answers
The possible change in volume (in mm3) resulting from the error in measuring the radius is 32. 06 mm³
Given,
A spherical golf ball is measured to have a radius of $$5 mm, with a possible measurement error of $$0.1 mm
How to determine the volume
The formula for volume of a sphere is expressed by;
Volume = 4/3 πr³
Where;
r is the radius of the sphere
pi takes the value 3.14
From the information given, we have that the measured radius is 5 mm, with a possible measurement error of 0.1 mm
Then, radius a = 5mm
Radius b = 5 + 0. 1 = 5. 01mm
Now, substitute the values into the formula
Volume, v = 4/ 3 (3.14)(5)³
v = 4/ 3 (392.5)
v = 523. 3 mm³
For radius of 5.01mm
Volume = 4/ 3 (3.14)(5.1)³
expand the bracket
Volume = 4/3 (416.52)
Volume = 555. 4 mm³
The change in volume = 555. 4 - 523. 3 = 32. 06 mm³
Hence, the change in volume is 32. 06 mm³
Learn more about Sphere's Volume at:
https://brainly.com/question/9994313
#SPJ4
When your gas tank is full, your car can drive 350 miles. If you’ve already driven 72 miles since the last time you filled up your gas tank, write an inequality representing the possible number of miles you can still drive in your car, then solve for the most amount of miles you can drive ?
Answers
Answer:
noentiendo. que preguntas?
Step-by-step explanation:
You are given that <1 and <3 are vertical angles with m<1=(4x-14) and m<3= 58
What is the value of x?
Please explain.
PLEASE HURRY I NEED THE ANSWER TO THIS
Answers
If we are given that ∠1 and ∠3 are vertical angles, we can conclude that m∠1 = m∠3, and we can use this information to solve for x in the given equation m∠1 = 4x - 14 = m∠3 = 58.
What is an inequality equation?
An inequality equation is a mathematical statement that compares two expressions using an inequality symbol such as < (less than), > (greater than), ≤ (less than or equal to), or ≥ (greater than or equal to).
Vertical angles are a pair of non-adjacent angles formed by the intersection of two straight lines.
They are always equal in measure, meaning that if angle A is a vertical angle to angle B, then the measure of angle A will always be equal to the measure of angle B.
This is because vertical angles are opposite each other and are formed by the same two intersecting lines.
Therefore, if we are given that ∠1 and ∠3 are vertical angles, we can conclude that m∠1 = m∠3, and we can use this information to solve for x in the given equation m∠1 = 4x - 14 = m∠3 = 58.
To know more about inequality equations visit:
https://brainly.com/question/30238989
#SPJ1
I set z=t=0(x,y,z,t)
and I got a partial solution (0,1,0,0).
I solved two homogeneous matrices once for z=1
and t=0
, then for z=0
and t=1
and I got two solutions (1,1,1,0)
and (1,1,0,1).
Then, I got (0,1,0,0)+a∗(1,1,1,0)+b∗(1,1,0,1
)
Therefore, all possible results are (0,1,0,0),(1,0,1,0),(1,0,0,1),(0,1,1,1)
Would this be correct?
Answers
The correct set of possible results would be (0, 1, 0, 0), (1, 2, 1, 0) and (1, 2, 0, 1).
Your approach seems to be correct, but there seems to be a minor mistake in your final list of possible solutions. Let's go through the steps to clarify.
Given the initial conditions z=t=0, you obtained a partial solution (0,1,0,0).
Next, you solved the homogeneous equations for z=1 and t=0, which resulted in a solution (1,1,1,0).
Similarly, solving the homogeneous equations for z=0 and t=1 gives another solution (1,1,0,1).
To find the general solution, you combine the partial solution with the solutions obtained in the previous step, using parameters a and b.
(0,1,0,0) + a(1,1,1,0) + b(1,1,0,1)
Expanding this expression, you get:
(0+a+b, 1+a+b, 0+a, 0+b)
Simplifying, you obtain the following set of solutions:
(0, 1, 0, 0)
(1, 2, 1, 0)
(1, 2, 0, 1)
Therefore, the correct set of possible results would be:
(0, 1, 0, 0)
(1, 2, 1, 0)
(1, 2, 0, 1)
Note that (0, 1, 1, 1) is not a valid solution in this case, as it does not satisfy the initial condition z = 0.
To learn more about set ,
https://brainly.com/question/30368748
#SPJ4
Solve for x in this problem √x-2 +4=x
Answers
The Radical Form (√x) ,the solutions to the equation √x - 2 + 4 = x are x = 1 and x = 4.
The equation √x - 2 + 4 = x for x, we can follow these steps:
1. Begin by isolating the radical term (√x) on one side of the equation. Move the constant term (-2) and the linear term (+4) to the other side of the equation:
√x = x - 4 + 2
2. Simplify the expression on the right side of the equation:
√x = x - 2
3. Square both sides of the equation to eliminate the square root:
(√x)^2 = (x - 2)^2
4. Simplify the equation further:
x = (x - 2)^2
5. Expand the right side of the equation using the square of a binomial:
x = (x - 2)(x - 2)
x = x^2 - 2x - 2x + 4
x = x^2 - 4x + 4
6. Move all terms to one side of the equation to set it equal to zero:
x^2 - 4x + 4 - x = 0
x^2 - 5x + 4 = 0
7. Factor the quadratic equation:
(x - 1)(x - 4) = 0
8. Apply the zero product property and set each factor equal to zero:
x - 1 = 0 or x - 4 = 0
9. Solve for x in each equation:
x = 1 or x = 4
Therefore, the solutions to the equation √x - 2 + 4 = x are x = 1 and x = 4.
To know more about Radical form .
https://brainly.com/question/29153583
#SPJ8
What expression should be used to access the first element of an array of integers called numbers? What expression should be used to access the last element of numbers, assuming it contains 10 elements? What expression can be used to access its last element, regardless of its length?
Answers
To access the first element of an array of integers called "numbers," you can use the expression:
numbers[0]`
This expression uses the array name "numbers" and the index "0" to access the first element.
To access the last element of "numbers," assuming it contains 10 elements, use the expression:
`numbers[9]`
Here, we use the index "9" since arrays are zero-indexed, meaning the last element in a 10-element array has an index of 9.
To access the first element of the array called numbers, we would use the expression "numbers[0]."
To access the last element of the array, assuming it contains 10 elements, we would use the expression "numbers [9]" since arrays are zero-indexed in most programming languages.
To access the last element of the array regardless of its length, we can use the expression "numbers [numbers.length-1]," which subtracts 1 from the length of the array to access the last element.
To access the last element, regardless of its length, use the expression:
'numbers [numbers. length - 1]'
This expression uses the "length" property of the array to find the total number of elements and subtracts 1 to get the correct index for the last element.
Learn more about Number:
brainly.com/question/17429689
#SPJ11
Point K is on line segment \overline{JL} JL . Given JK=5x+7,JK=5x+7, JL=2x+8,JL=2x+8, and KL=4,KL=4, determine the numerical length of \overline{JL}. JL .
Answers
Answer:
JL = 6 units
Step-by-step explanation:
It is given that,
K lies on line segment JL.
We have, JK=5x+7,JL=2x+8, and KL=4.
JL = JK + KL
2x+8 = 5x+7 + 4
Taking like terms together.
8-7-4=5x-2x
-3 = 3x
x = -1
Put x = -1 in JL = 2x+8. So,
JL = 2(-1)+8
JL = 6
Hence, the length of JL is 6 units.
Simplify by combining like terms: 3x + 2 + x + 7
A. 5x + 7
B. 3x + 9
C. 4x + 9
D. 6x + 7
Answers
3x and x are like terms
And 2 and 7 are like terms
Hope this helps :D
i need help 25 points
Determine the length of the line segment shown.
13 units
39 units
100 units
169 units

Answers
Answer: Try A; 13 units
Step-by-step explanation:
count the number of units
Use the given information to prove that

Answers
A line segment can be made up of the addition of different fractions of the line on a straight path i.e a given line segment can be broken into smaller parts.
Therefore, the required proof that EG = HK is shown below:
Given that: EF = JK
FG = HJ
But,
EG = EF + FG .............. 1
and
HK = HJ + JK ............. 2
From equation 1, we have:
EG = EF + FG
= JK + HJ (since EF = JK, and FG = HJ)
So that,
EG = JK + HJ ........... 3
Also from equation 2, we have:
HK = HJ + JK
= FG + EF (since EF = JK, and FG = HJ)
So that,
HK = FG + JK ........... 4
Therefore, comparing equations 1, 2, 3, and 4, it can be concluded that;
EG = HK
For more clarifications on fractions of a line segment, visit: https://brainly.com/question/17374569
#SPJ1
I have 0 clue how to do this

Answers
Answer:
okay, I'll explain how to do it.
y = 4x
so make a table
-1. -4
0. 0
1. 4
plot those points and draw a line through them.
let's plot some points to start.
Which comparison is not correct?
8 > -9
-7 > -9
-8 < -4
-2 < -9
Answers
Answer:
-2>-9
The larger the negative numbers , the smaller it is
A two-digit number read from left to right is 20% greater than the same number read from right to left. Find the number.
Answers
Answer:
54
Step-by-step explanation:
We'll call the number "ab".
From left to right, the value of this number will be \(10a+b\).
From right to left, the value of this number will ve \(10b+a\).
From the question,
\(10a+b=1.2(a+10b)\\10a+b=1.2a+12b\\8.8a=11b\)
For a and b to be whole numbers,
\(\left \{ {{a=5} \atop {b=4}} \right.\)
So the number is 54.