If x = 4, calculate the value of: 2x³ - 2x² + 2x - x
Answers
Step-by-step explanation:
Putting value of x
2 (4)3 - 2(4)2 + 2(4) - 4
2 (64) - 2(16) + 8 - 4
128 - 32 + 8 - 4
= 100
Answer:
i dunno try this sorry if its wrong. Answer i got is 16.
Step-by-step explanation:
since the x = 4 and we need to calculate the value of other numbers. my answer would be this,
2 x 2 x 2 = 6, 2 x 2 = 4 add both values up to get 10, then do 10 x 2 which is 20, - 4 since x is 4.
Also i did this the way you would write it in exponent form.
Related Questions
Evan bought a book on training for a triathlon. The book cost $13.95. He gave the cashier a $20 bill. How much
change did he receive?
20.00
- 13.95
$6.05
O $7.05
O $7.50
$11.95
Answers
Answer: He received $6:05.
Step-by-step explanation:
I got this by subtracting $13.95 from $20.00.
Derek is solving the problem below for this whole 712÷1118 is equal to
Answers
Answer:
\(\frac{356}{559}\)
I hope this helps!
the number in each block is the sum of the numbers in the two blocks beneath it. Some of the numbers are hidden. What is the value of y - x

Answers
Answer:
y - x = 69
Step-by-step explanation:
From the figure attached,
Number in each block is the sum of the numbers in the block beneath it.
Therefore, A + 21 = 32 ⇒ A = 11
A + 5 = B ⇒ B = 16
C = 5 + x
D = 32 + B ⇒ D = 32 + 16 = 48
E = B + C ⇒ E = 16 + (5 + x)
⇒ E = 21 + x
y = D + E ⇒ y = 48 + (21 + x)
y = 48 + 21 + x
y = 69 + x
y - x = 69
Therefore, y - x = 69 will be the answer.

The earrings that Mrs.Moore wants to buy are $55.00. She won’t buy them until they are at least 45% off. What is the most that Mrs.Moore is willing to spend?
Answers
Answer:
$30.25
Step-by-step explanation:
55% of 55$ is $30.25. she wants 45 % off of 55$. which is $24.75. 55-24.75 is 30.25
$30.25
since it's 45% off, you need to subtract 45% from 100%
100%-45%=55%
then turn the % into a decimal
55%/100=0.55
now multiply the original price by 0.55
0.55*55=30.25

On a piece of paper graph f(x) = 3x. Then determine which answer choice matches the graph you drew

Answers
Answer:
--
Step-by-step explanation:
Show all the options please
Not able to see all options
Question in the pic, please explain your answer

Answers
The statement translated to an algebra equation will give the value of the unknown number w = 11/5
What is algebra?Algebra is the branch of mathematics that helps to represent problems or values in the form of mathematical expressions using letters to represent unknown values.
Let us represent the unknown number with the letter w so that the statement can be written as the equation:
5w - 8 = 3
add 8 to both sides
5w - 8 + 8 = 3 + 8
5w = 11
divide through by 5
5w/5 = 11/5
w = 11/5
Therefore, the statement translated to an algebra equation will give the value of the unknown number w = 11/5
Read more about algebra here: https://brainly.com/question/4344214
#SPJ1
Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.
Write with fractional exponents. (Do not use parentheses.)

Answers
Answer:
4\(y^{\frac{3}{2} }\)
Step-by-step explanation:
using the rule of exponents/ radicals
\(\sqrt[n]{a^{m} }\) = \(a^{\frac{m}{n} }\)
then
4 \(\sqrt{y^{3} }\)
= 4\(y^{\frac{3}{2} }\)
Missy is wrapping a gift for her sister's birthday in a box with the dimensions shown.
17.5 in.
4 in.
10 in.
What is the minimum amount of wrapping paper she will need to completely cover the box?
Answers
Missy will need a minimum of 570 square inches of wrapping paper to completely cover the box.
To calculate the minimum amount of wrapping paper needed to cover the box, we need to find the surface area of the box.
A rectangular box has six sides: a top, a bottom, two sides, and two ends.
The top and bottom sides have the same dimensions, which are 17.5 inches by 10 inches. So each of these sides has an area of 17.5 in × 10 in = 175 square inches.
The two side surfaces also have the same dimensions, which are 17.5 inches by 4 inches.
Each of these sides has an area of 17.5 in × 4 in = 70 square inches.
The two end surfaces have the same dimensions, which are 10 inches by 4 inches. Each of these sides has an area of 10 in × 4 in = 40 square inches.
To find the total surface area of the box, we add up the areas of all six sides:
175 in² (top) + 175 in² (bottom) + 70 in² (side 1) + 70 in² (side 2) + 40 in² (end 1) + 40 in² (end 2)
Total surface area = 570 in².
To learn more about the surface area of the cuboid;
https://brainly.com/question/26403859
#SPJ1
Passing through (4,5) and PARALLEL to y=2x-4
Answers
A PARALLEL line has the same angular coeficient, so:
\(f(x) = 2x+b\)
\(f(4) = 5\)
\(5 = 2\cdot 4 +b\)
\(b = 5-8\)
\(b = -3\)
The line asked is:
\(f(x) = 2x-3\)
Answer:
-2x+y=-3
Step-by-step explanation:
Choose a point (4,5) that the parallel line will pass through.
Find the slope m=2
To find an equation that is parallel to y=2x-4 the slopes must be equal. Using the slope of the equation, find the parallel line using the point-slope formula.
y-y1=m(x-x1) if m=2 and x1=4 and y1=5
y-5=2(x-4)
y-5=2x-8
Solve for y --- > y=2x-3
-2x+y=-3
(-2x+y=-3)*-1
2x-y=3
I need help with my pre-calculus homework, could you show me how to solve this inequality? The image of the problem is attached.Solving Polynomial InequalitiesDirections: Copy each inequality onto a piece of paper and solve.

Answers
-The answer is:
\((-\infty,-1)\cup(4,\infty)\)This is a quadratic expression, factored out. The roots are:
\(\begin{gathered} x-4=0\Rightarrow x=4 \\ x+1=0\Rightarrow x=-1 \end{gathered}\)This tell us that the function in x 0 -1 and x = 4 is equal to zero. We what to find all the x for which the function is positive.
If we grapf the points in a line:
The red point are the places where the function is zero. We want to know what happends between those points. If the function is positive between -1 and 4, then the answer would we that interval. If the function is negative in that interval, then we want to know if the function is positive outside the interval:
Let's take a point between -1 and 4 and to make simpler: x = 0
Let's see whats the value: (0 - 4)(0 + 1) = (-4) * 1 = -4
It's negative, then the inequality (x - 4)(x +1) > 0 is false in the interval (-1, 4)
Let's see what happends outside the interval (-1, 49. Let's take the points x = -5 and x = 5, because -5 < -1 and 4 < 5
(5 - 4)(5 +1) = 1 * 6 = 6 It's positive.
(-5 - 4)(-5 + 1) = (-9)(-4) = 36 It's positive.
Then the answer are all the x's smaller than -1 and greater than 4.

Help please guys this is so hard pleaes help

Answers
===================================================
Explanation:
Check out the diagram below.
The original L shape is indicated as "figure A".
Split the L shape into 2 rectangular prisms (aka blocks) labeled figure B and figure C. For now, we'll ignore the red regions, but we'll come back to that later.
Figure B is a block with dimensions of
L = length = 5W = width = 10H = height = 30The surface area is:
SA = 2*(L*W + L*H + W*H)
SA = 2*(5*10 + 5*30 + 10*30)
SA = 1000 square cm
-----------------------
Now move your attention to figure C.
L = length = 12W = width = 5H = height = 10SA = 2*(L*W + L*H + W*H)
SA = 2*(12*5 + 12*10 + 5*10)
SA = 460 square cm.
----------------------
When combining those two surface areas (of figures B and C) we get a total surface area of 1000+460 = 1460 square cm.
But wait, we need to account for those red regions I mentioned earlier.
This region is not frosted as it's inside the cake rather than on the outside.
The area of the red rectangle is 10*5 = 50 sq cm. It's counted twice when we combined the two 3D blocks together to form the L shape again.
So we have to subtract off 2*50 = 100 sq cm to ignore the red region.
1460-100 = 1360 square cm is the final answer.

How many 2-letter words can be made from the letters MATH if
Answers
Answer:
ham
tam
mat
hat
at
ha
am
ma
Step-by-step explanation:
The average cost of tuition plus room and board for a small private liberal arts college is reported to be $9,200 per term, but a financial administrator believes that the average cost is higher. A study conducted using 350 small liberal arts colleges showed that the average cost per term is $9,515. The population standard deviation is $1,200. Let α = 0.05. Based on the computed test statistic or p-value, what is our decision about the average cost?
1. Equal to $9,200
2. Greater than $9,200
3. Less than $9,200
4. Not equal to $9,200
Answers
Suppose that y varies inversely with x. Use the information to find k, and then choose the equation of variation.x = 2
when y = 11.
a) k=2/11, y=2/11x
b) k=22, y=22/x
c) k=11/2, y=11x/2
d) k=11/2,y=11/2x
Answers
Since the product of variables in inverse proportion is constant, the equation is \(xy=22\)
Dividing both sides by x, we get:
\(\boxed{y=\frac{22}{x}} \longrightarrow k=\boxed{22}\)
Given that a+b = 10 and a square - b square = 40 find the value of a-b
Answers
Answer:
the value of a - b is 4.
Step-by-step explanation:
We have been given the following two equations:
a + b = 10 ------------(1)
a² - b² = 40 -------(2)
We can factor the left-hand side of equation (2) using the difference of squares identity:
(a + b)(a - b) = 40
Substituting equation (1) into this equation, we get:
10(a - b) = 40
Dividing both sides by 10, we get:
a - b = 4
Therefore, the value of a - b is 4.
Step-by-step explanation:
if I understand this correctly :
a + b = 10
a² - b² = 40
(a² - b²) = (a + b)(a - b) = 40
10(a - b) = 40
(a - b) = 4
Given vectors a = (2, 6) and b = (-3, 4), find – 3 a +5b.
Write your answer in component form.
Answers
Answer:
\(\huge\boxed{-3\overrightarrow{a}+5\overrightarrow{b}=\left<-21;\ 2\right>}\)
Step-by-step explanation:
\(\overrightarrow{a}=\left<2;\ 6\right>\\\\\overrightarrow{b}=\left<-3;\ 4\right>\\\\-3\overrightarrow{a}+5\overrightarrow{b}=-3\left<2;\ 6\right>+5\left<-3;\ 4\right>=\left<-3\cdot2;\ -3\cdot6\right>+\left<5\cdot(-3);\ 5\cdot4\right>\\\\=\left<-6;\ -18\right>+\left<-15;\ 20\right>=\left<-6+(-15);\ -18+20\right>=\left<-21;\ 2\right>\)
if x-y = 8 and xy=5 , find x^2 + y^2
Answers
Answer:
x² + y² = 74
Step-by-step explanation:
given
(x - y) = 8 ( square both sides )
(x - y)² = 8² ← expand left side using FOIL
x² - 2xy + y² = 64 ← substitute xy = 5
x² - 2(5) + y² = 64
x² - 10 + y² = 64 ( add 10 to both sides )
x² + y² = 74
Anyone know how to do this?
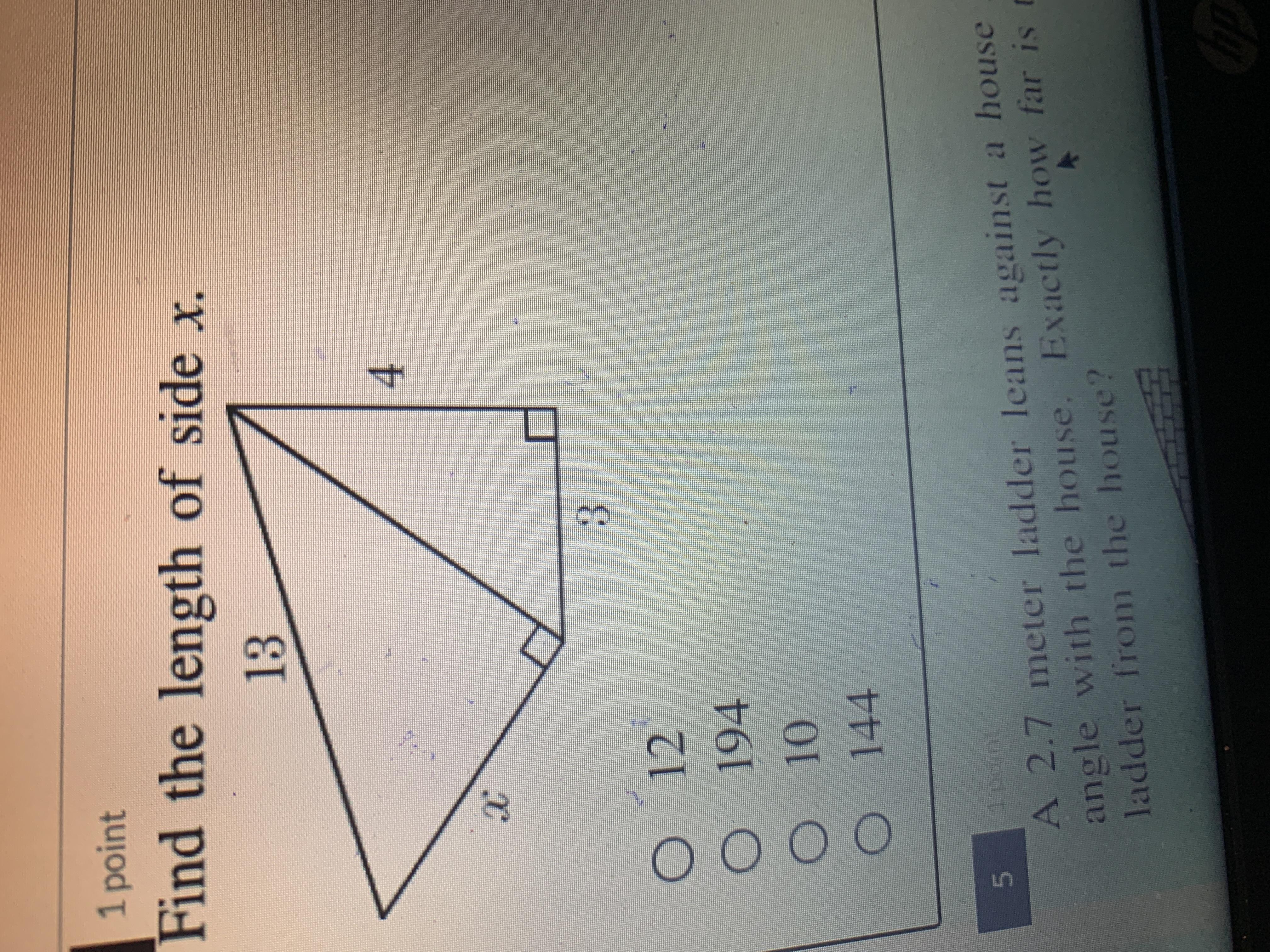
Answers
Answer:
It would be 10
Step-by-step explanation:
Its 10 because 12 is to long and the fact that 10 is a few inches shorter it looks correct :D
Answer:
A) 12
Step-by-step explanation:
Yes you have to do a² + b² = c²
So the bottom triangle is 3 and 4 so plug in.
4² + 3² = c² (simplify)
16 + 9 = c²
25 = c² (square root both sides)
5 = c
That gives us the vertical side of the second triangle.
So plug in again
5² + b² = 13² (simplify)
25 + b² = 169 (subtract 25 on both sides)
b² = 144 (square root both sides)
b = 12
x = 12
Hope this helps ya!!
Plz show work thanks

Answers
Answer:
1/sec x- tan x
Step-by-step explanation:
sec x+ tan x
= sec x+ tan x) (sec x - tan x)/(sec x , tan x)
=sec^2x-tan^2x)(sec x- tan x)
(sec^2x-tan^2x=1)
=1/sec x- tan x
Which product range generated the most profit over all???

Answers
Answer:
Blue label
Step-by-step explanation:
All that matters here is # of bottles sold * profit per bottle.
If you multiply these 2 values for each row you will see the blue label has the highest amount of profit.
Among all the product ranges blue label generated the most profit of $5625.
What is profit?Profit is basically the difference between the total revenue and the total cost of the product.
Profit=Total Revenue- Total cost.
How to calculate profit?We know that Average profit= total profit/ number of units.
So the profit will be as average profits* number of units.
So the profit of product ranges will be =average profit * number of bottles.
Profit of red label=1.12*3000
=$3360
Profit of black label=1.5*2000
=$3000.
Profit of gold label=2.75*1000
=$2750
Profit of white label=1.20*2750
=$3300
Profit of blue label=2.25*2500
=$5625.
Hence among all the product ranges blue label has generated maximum profit.
Learn more about profit at https://brainly.com/question/1078746
#SPJ2
the linear equation 5( + 9) = 5 +45.
Answers
Answer:
45 = 50
not true
Answer: 45=50
Step-by-step explanation:
how oes the relationship between logarithms and exponential functions help us find solutions

Answers
The relationship between logarithms and exponential functions is fundamental and provides a powerful tool for finding solutions in various mathematical and scientific contexts.
Logarithms are the inverse functions of exponential functions. They allow us to solve equations and manipulate exponential expressions in a more manageable way. By taking the logarithm of both sides of an exponential equation, we can convert it into a linear equation, which is often easier to solve.
One of the key properties of logarithms is the ability to condense multiplication and division operations into addition and subtraction operations. For example, the logarithm of a product is equal to the sum of the logarithms, and the logarithm of a quotient is equal to the difference of the logarithms.
Logarithms also help us solve equations involving exponential growth or decay. By taking the logarithm of both sides of an exponential growth or decay equation, we can isolate the exponent and solve for the unknown variable.
This is particularly useful in fields such as finance, population modeling, and radioactive decay, where exponential functions are commonly used.
Furthermore, logarithms provide a way to express very large or very small numbers in a more manageable form. The logarithmic scale allows us to compress a wide range of values into a smaller range, making it easier to analyze and compare data.
In summary, the relationship between logarithms and exponential functions enables us to simplify and solve equations involving exponential expressions, model exponential growth or decay, and manipulate large or small numbers more effectively.
For more such question on logarithms visit:
https://brainly.com/question/25993029
#SPJ8
a billboard designer has decided that a sign should have 5-ft margins at the top and bottom and 2-ft margins on the left and right sides. furthermore, the billboard should have a total area of 150 ft2 (including the margins). if x denotes the width (in feet) of the billboard, find a function in the variable x giving the area of the printed region of the billboard.
Answers
If x denotes the width (in feet) of the billboard, find a function in the variable x giving the area of the printed region of the billboard as a function of x is (150/x - 10)(x - 4).
A billboard designer has decided that a sign should have 5-ft margins at the top and bottom and 2-ft margins on the left and right sides.
x = width of the billboard designer
Total Area including margin = 150 ft^2
Height of the billboard = Area/width
Height of the billboard = 150/x
Before the height of the billboard = (150/x - 5 × 2)
Before the height of the billboard = (150/x - 10) ft
The width of the printed region billboard = (x - 2 × 2)
The width of the printed region billboard = (x - 4) ft
The area of the printed region of the billboard = The width of the printed region billboard × The height of the printed region billboard
The area of the printed region of the billboard = (150/x - 10)(x - 4)
To learn more about area of rectangle link is here
brainly.com/question/20693059
#SPJ4
The complete question is:
A billboard designer has decided that a sign should have 5-ft margins at the top and bottom and 2-ft margins on the left and right sides. Furthermore, the billboard should have a total area of 150 ft^2 (including the margins).
If x denotes the width (in feet) of the billboard, find a function in the variable x giving the area of the printed region of the billboard.
Area as a function of x =

PLEAS HELP
Questions
1. A company secretary has an investment opportunity in which a lending institution offers her an interest
rate of 4.0% compounded quarterly. If she decides to invest an amount of K6000 under the scheme for 8
years, calculate:
(a) the accumulated factor
(b) the accumulated value
(c) the total compound interest earned
[2 marks]
[2 marks]
[2 marks]
2. Suppose the lending institution in question 1 offers the secretary an alternative deal in which she would
earn simple interest at a rate of 4.6% per annum over 8 years. Which deal should she accept?
[5 marks]
3. Suppose that K200 has amounted to K310 in 10 years with interest compounded semi-annually. What
annual rate of compound interest was used?
[4 marks]
4. A UOG tutor is anxious to purchase a used car, for which he estimates that will need a total of K8000. He
currently has K6200 and is offered two different investment plans, A and B. Under Plan A he would be paid
simple interest at an annual rate of 5.4%, and under Plan B he would be paid an annual interest rate of 4.8%
compounded monthly.
Under each plan, how long would it be before he reached his target of K8000?
[6 marks]
Page 1 of 2
5. An amount of K5000 is invested at an interest rate of 4% per annum, compounded annually. Find the
accumulation factor, the accumulated value and total amount of compound interest earned after:
(a) 2 years
[6 marks]
(b) 5 years
[6 marks]
6. A retired police officer invests K5000 in a credit union that pays an interest rate of 5% per annum,
compounded quarterly. Exactly 2 years later she invests a further K6000 with the credit union under the
same conditions. How much total interest will she have earned 5 years after the original investment?
[10 marks]****
7. The Bank South Pacific Limited is offering ‘unbeatable deals’ on its savings accounts, where it will pay
investors interest that is compounded quarterly at an annual rate of 4%. Sharon wants to save K10 000 to
purchase a car, but has only K8000 to invest in the savings account on 1 June 2001. Under the bank’s deal,
on approximately what date will Sharon reach her target?
[4 marks]
8. Mr Simon Kila opens a shopfront business where he will lend money to anyone (without security) if they
are willing to pay his interest rate of 2% per week compounded daily. The first customer borrows K5000 to
buy a used car, but is unable to pay Mr Simon Kila back for 12 weeks. How much will the customer have to
pay back at this time?
Answers
1a. The accumulated factor is 1.5986.
b. The accumulated value is K9591.60
c. The total compound interest earned is K3591.60.
2. Deal 1 is better since it gives a higher amount, K3591.60, of interest earned compared to Deal 2, of K2273.60.
3. The annual compound interest rate used is 5.42%.
4a. Under Plan A, it would take 5.38 years to reach his target of K8000.
b. It would take him 3.65 years to reach his target. under Plan B.
5a. Accumulation factor is 1.0816, accumulated value is K5408, and the total compound interest earned is K408.
b. Accumulation factor is 1.2167, the accumulated value is K6083.50, and the total compound interest earned is K1083.50
6. Total interest she will earn 5 years after the original investment is K4,595.69.
7. Sharon will reach her target in approximately June 2002 which is approx. 1.07 years.
8. The customer will have to pay back K6757.61 after 12 weeks.
How to compute compound interest?1. (a) The accumulated factor is calculated as follows:
i = 4.0% per year, compounded quarterly
n = 8 years × 4 quarters per year = 32 quarters
Using the formula for the accumulated factor for quarterly compounding:
F = \((1 + i)^{n}\) = \((1 + 0.04/4)^{32}\) = 1.5986
Accumulated factor = 1.5986.
(b) Accumulated value: accumulated factor * principal amount:
A = F × P = 1.5986 × K6000 = K9591.60
Accumulated value = K9591.60.
(c) The total compound interest earned: principal -accumulated value:
I = A - P = K9591.60 - K6000 = K3591.60
Compound interest earned =K3591.60.
2. To compare the two deals, we will calculate the total amount of interest earned under each one.
Under Deal 1, interest is compounded quarterly:
I = A - P = K9591.60 - K6000 = K3591.60
Under Deal 2: We shall use the formula: I = P × r × t
P = principal amount,
r = interest rate,
t = time in years.
I = K6200 × 0.046 × 8 = K2273.60
This means that the first deal is better since it gives a higher total amount of interest earned.
3. The annual interest rate:
Given::
P = K200
A = K310
n = 2 (compounded twice per year)
t = 10 years
A = \(P (1 + r/n)^{(nt)}\)
A = accumulated value,
P = principal amount,
r = interest rate,
n = number of times the interest is compounded per year,
t = time in years.
310 = \(200 (1 + r/2)^{(2 * 10)}\)
1.55 = \((1 + r/2)^{20}\)
Taking the 20th root of both sides, we get:
1 + r/2 = 1.0271
r/2 = 0.0271
r = 0.0542
Annual compound interest rate = 5.42%.
4. (a) Under Plan A,
Using I = P × r × t, we have:
I = K8000 - K6200 = K1800
r = 5.4%
t = I / (P × r) = K1800 / (K6200 × 0.054) = K334.80
To reach K8000, the tutor will need to earn K1800 in interest, so he is to invest for:
K1800 / K334.80 = 5.38 years
(b) Under Plan B, interest is compounded monthly. using the formula A = \(P (1 + r/n)^{(nt)}\)
Monthly interest rate:
0.048 / 12 = 0.004
The amount of interest earned in one month is:
K6200 x 0.004 = K24.80
To reach K8000, the tutor will need to earn K1800 in interest, so he has to invest for:
log(K8000/K6200) / log(1+0.004) = 43.76 months
= 43.76/12
= 3.65 years.
5(a) After 2 years, the accumulation factor is:
\((1 + 0.04)^{2}\) = 1.0816
The accumulated value is:
K5000 x 1.0816 = K5408
Total compound interest earned is:
K5408 - K5000 = K408
(b) After 5 years, the accumulation factor is:
(1 + 0.04)⁵ = 1.2167
The accumulated value is:
K5000 x 1.2167 = K6083.50
The total amount of compound interest earned is:
K6083.50 - K5000 = K1083.50
6. Amount invested is K5000 + K6000 = K11,000.
Interest rate = 5% per annum compounded quarterly, so the quarterly interest rate is 1.25%.
The number of quarters in 5 years is 20.
Accumulated value after 5 years is:
\(K11,000 (1 + 0.0125)^{20}\) = K15,595.69
The total interest earned is:
K15,595.69 - K11,000 = K4,595.69
7. To calculate the time taken to reach K10,000, we use the compound interest formula:
\(K8000 (1 + 0.04/4)^{4t}\) = K10,000
where t = time in years.
t = log(K10,000/K8000) / (4 log(1 + 0.04/4)) = 4.28 quarters
4 quarters in a year is ≈ 1.07 years, so Sharon will reach her target in approximately June 2002.
8. Weekly interest rate = 2%,
So daily interest rate ≈ 0.0286%.
The amount owed after 12 weeks:
\(K5000 (1 + 0.000286)^{84}\) = K6757.61
The customer will pay back K6757.61 after 12 weeks
Learn more about compound interest at brainly.com/question/28020457
#SPJ1
If 84 of the 224 participants in club activities are nonresidents what is the ratio of residents to nonresidents who participate in club activities
Answers
Answer:
5:3
Step-by-step explanation:
140:84 =
35:21 =
5:3
Hope that helps! (If you're up for it, can you give me a brainliest? Thanks)
The ratio is 5:3
What is ratio?A ratio indicates how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six.
Given:
Total participants= 224
nonresidents =84
So, residents= 224-84 = 140
Now, ratio of residents to nonresidents
=140/84
=70/42
=10/6
=5/3
Learn more about ratio here:
https://brainly.com/question/26974513
#SPJ6
Find the amount (future value) of the ordinary annuity. (Round your answer to the nearest cent.)
$300/week for 9 1/2
years at 5.5%/year compounded weekly
Answers
Answer: $227,226.51
Step-by-step explanation:
First, we need to convert the period to weeks.
9 1/2 years = 9.5 years
1 year = 52 weeks
9.5 years = 494 weeks
Next, we can use the formula for the future value of an annuity:
FV = (PMT x (((1 + r/n)^(n*t)) - 1)) / (r/n)
where:
PMT = payment amount per period
r = annual interest rate
n = number of compounding periods per year
t = number of years
Plugging in the given values:
PMT = $300
r = 0.055 (5.5% expressed as a decimal)
n = 52 (compounded weekly)
t = 9.5 years = 494 weeks
FV = ($300 x (((1 + 0.055/52)^(52*494)) - 1)) / (0.055/52)
FV = $227,226.51
Therefore, the future value of the annuity is approximately $227,226.51.
Need help please!!! it’s important

Answers
Answer:
4/D a reflection fallowed by a rotation.
sorry if I am wrong
4/5 • 5/4 = 1 Determine the property illustrated.
Answers
The algebraic property illustrated is the commutative property of multiplication
What are the properties of algebra?
The properties of algebra are those properties mostly used in simplifying algebraic expressions.
Algebraic properties are:
Commutative property of additionCommutative property of multiplicationAssociative property of additionAssociative property of multiplicationDistributive Properties of Addition Over MultiplicationFrom the expression given we have
4/5 • 5/4 = 1
= 4/ 5 × 5/ 4
= 1
Thus, the algebraic property illustrated is the commutative property of multiplication
Learn more about algebraic property here:
https://brainly.com/question/855307
#SPJ1
Hannah took a taxi from her house to the airport. The taxi company charged a pick-up fee of $1.90 plus $3.75 per mile. The total fare was $80.65, not including the tip. Write and solve an equation which can be used to determine mm, the number of miles in the taxi ride.
Answers
Answer: y=3.75x+1.9
Step-by-step explanation: the pick up fee would be the y-intercept and the per mile cost would be the slope.
The equation that can be used to determine the number of miles in the taxi ride is 1.90 + 3.75x = 80.65.
The number of miles traveled is 21 miles.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
We have,
Pick up fee charges = $1.90
Charges per mile = $3.75
Total fare = $80.65
The number of miles traveled = x
We can write an equation as:
1.90 + 3.75x = 80.65
The number of miles traveled:
1.90 + 3.75x = 80.65
Subtract 1.90 on both sides.
1.90 + 3.75x - 1.90 = 80.65 - 1.90
3.75x = 78.75
Divide both sides by 3.75.
x = 21.
Thus,
The equation that can be used to determine the number of miles in the taxi ride is 1.90 + 3.75x = 80.65.
The number of miles traveled is 21 miles.
Learn more about equations here:
https://brainly.com/question/14686792
#SPJ2
Joni has a box that has a mass of 67 dekagrams.she converts to centigrams.her work is shown below.67/100=0.067.which statement best explains Joni's error.
Answers
hello
according to metric table
1 decagram = 1000 centigram
Joni's mistake was not multiplying by 1000
the answer is option B